Санкт-Петербургский Государственный Университет
Факультет прикладной математики – процессов управления
Кафедра диагностики функциональных систем
Анализ зависимости между УК в крови больных СКВ и степенью тяжести поражения почек
Курсовая работа
Варламова
Александра
Александровна
Научный руководитель
доктор медицинских наук, профессор Шишкин В.И.
Санкт-Петербург 2008
Содержание
§1. Введение
§2. Постановка задачи
§3. Используемые методы
1. Дисперсионный анализ по одному признаку для проверки равенства нескольких средних
2. Непараметрический дисперсионный анализ по одному признаку с применением критерия Краскала-Уоллиса для нескольких независимых выборок
3. Непараметрический дисперсионный анализ по одному признаку с применением критерия Джонкхиера для нескольких выборок, упорядоченных по возрастанию влияния фактора
§4.Вывод
§5. Список литературы
§1. Введение
Формулировка проблемы
Изложим проблемную ситуацию, имеющую место в настоящее время в решении задач обработки результатов исследований. Известно, что в распоряжении исследователей имеется большая и постоянно растущая в объеме база данных результатов измерений из разных областей естествознания: астрономии, экспериментальной физики, экономики, биологии, медицины.
По мнению автора, сформировавшемуся вследствии ознакомления с содержанием официальных высказываний ведущих политиков и ученых мира, наибольшего развития в 21 веке среди других наук достигнут биология и медицина. Известно и напечатано, например, в книге Е.В. Гублера "Информатика в патологии, клинической медицине и педиатрии" [1] , что в этом аспекте решение задач обработки результатов измерений приобретает ключевое значение . Следуя рекомендациям пособия "Кандидатская диссертация" [2] выполним критический анализ ситуации, сложившейся в настоящее время в России в решении задач обработки результатов наблюдений. Уже на предварительном этапе исследования имеет место противоречивая ситуация: с одной стороны – обработка найденных в медицине результатов измерений является актуальной задачей в современной науке, с другой стороны – известно, что в медицинских ВУЗах математика, как дисциплина учебного процесса , практически не изучается. Следовательно, то что методы обработки данных медицинских исследований стали предоставляться математикам-специалистам, создает прецедент выдвижения медицины в число приоритетных направлений Российской науки.
Изложив проблемную ситуацию, перейдем к определению цели и объекта исследования.
§2. Постановка задачи
Предварительные замечания
Системные заболевания соединительной ткани, такие как системная красная волчанка , характеризуются прежде всего выраженной патологией по иммунологической компоненте. Мониторинг этого контингента больных позволяет отнести системные заболевания к числу крайне тяжелых недугов, поражающих людей в наиболее деятельный возрастной период ( в среднем 30-50 лет )[8] и приводящих к ранней инвалидизации, а порой и к летальным исходам. Усиливающееся год от года неблагоприятное воздействие окружающей среды приводит к росту иммунодефицитов различной этиологии, в том числе возрастает заболеваемость системными вариантами иммунокомплексных патологий.
В иммунокомплексных патологиях система комплемента играет важную, хотя и не всегда ясную, роль. Таким образом изучение динамики комплемента приобретает ключевое теоретическое и практическое значение. В связи с этим нами предпринят анализ зависимости уровня комплемента с тяжестью течения классического иммунокомплексного заболевания системной красной волчанкой.
Объект, предмет, цель и задача исследования
В качестве исходных данных для исследования даны выборки численных значений медико-биологических показателей человеческого организма, а именно: уровня комплемента в крови больных системной красной волчанкой ( в дальнейшем – СКВ) и степенью тяжести поражения почек. . В целях полноты изложения приведем необходимое определение : "Комплемент - система сывороточных белков, которая активируется комплексом антиген - антитело с образованием биологически-активных веществ, способных вызывать необратимые повреждения клеточных мембран. Комплемент является одним из факторов естественного иммунитета и широко применяется в диагностических иммунологических реакциях."[3, ст. 57]
Объектом нашего исследования являлись выборочные данные результатов измерений уровня комплемента ( в дальнейшем - УК), причем изучаемые данные представляют собой пять столбцов чисел ,в первом из которых представлены данные без нефрита, во втором с нефритом слабовыраженным, в третьем с нефритом средней выраженности, в четвертом с нефротическим синдром, а в пятом- с почечной недостаточностью.
Предмет исследования определяем, как нахождение зависимости УК в крови больных СКВ и степенью тяжести поражения почек.
§3. Используемые методы
Будем использовать методы биометрического анализа, основанные на проверке гипотез однородности выборок.[9]
1.
Дисперсионный анализ по одному признаку для проверки равенства нескольких средних
Во многих случаях практики интерес представляет вопрос о том, в какой мере существенно влияние того или иного фактора на рассматриваемый признак [9]. В данном случае фактором является степень поражения почек, а признаком - УК.
Научное обоснованное решение подобной задачи при некоторых предположениях составляет предмет дисперсионного анализа , введенного математиком- статистиком Р. А. Фишером.[10]
Статистическая модель
Выборки производятся из нормальных совокупностей. Первая выборка производиться из совокупности со средним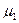 , вторая - со средним , вторая - со средним 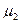 , k-я из совокупности со средним , k-я из совокупности со средним 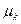 . Все наблюдения независимы. Будем считать распределение данной мне совокупности нормальным. . Все наблюдения независимы. Будем считать распределение данной мне совокупности нормальным.
Гипотезы №1.
Н0
: 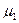 = = 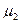 =…= =…= 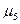
Н1
: не все средние равны. все средние равны.
Критическая область.
Верхняя 5%-ная область Fk-1.
N
-
k
-распределения. В нашем случае F4,474
-распределения, так как k=4, а 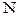 =n1
+ n2
+ n3
+ n4
+ n5
=479. Эта область определяется неравенством F>2.37. ( Определяется по таблице, см. Таблица А.4а на стр. 334 "Справочника по вычислительным методам статистики" Дж. Поллард [6] ) =n1
+ n2
+ n3
+ n4
+ n5
=479. Эта область определяется неравенством F>2.37. ( Определяется по таблице, см. Таблица А.4а на стр. 334 "Справочника по вычислительным методам статистики" Дж. Поллард [6] )
Вычисление значения критериальной статистики
Будем рассматривать исходные данные, представленные Таблицей №1.
Таблица №1.
Значения УК в зависимости от тяжести ГН.
.Нет нефрита
Выборка объема
n1
= 210
|
Слабый нефрит
Выборка объема n2
= 101
|
Средний нефрит
Выборка объема n3
= 98
|
Нефротический синдром
Выборка объема
n4
= 45
|
Почечная недостаточность
Выборка объема
n5
= 25
|
| 36 |
11 |
7 |
10 |
20 |
| 38 |
35 |
27 |
5 |
20 |
| 40 |
37 |
6 |
6 |
21 |
| 31 |
15 |
5 |
15 |
24 |
| 33 |
40 |
40 |
20 |
3 |
| 33,8 |
0 |
5 |
25 |
12 |
| 37 |
33 |
45 |
28 |
10 |
| 38 |
33 |
45 |
32 |
0 |
| 33 |
5 |
46 |
46 |
18,2 |
| 37 |
40 |
45 |
33 |
46 |
| 48 |
25 |
24 |
44 |
10 |
| 40 |
33 |
24 |
25 |
0 |
| 42 |
50 |
43 |
22,5 |
20 |
| 35 |
25 |
24,5 |
24,5 |
30,4 |
| 15 |
20 |
20,5 |
38 |
0 |
| 35 |
50 |
9 |
12 |
33,3 |
| 48 |
50 |
12 |
54,7 |
14,7 |
| 45 |
18 |
32 |
20,7 |
34,1 |
| 38 |
20 |
43 |
0 |
22,4 |
| 15 |
33 |
35,5 |
26,1 |
17,8 |
| 13 |
43 |
44 |
11 |
33,5 |
| 40 |
10 |
50 |
11,7 |
29,6 |
| 40 |
12 |
34 |
34,4 |
13,6 |
| 38 |
23 |
12 |
0 |
35 |
| 32,7 |
34 |
0 |
0 |
37 |
| 60 |
30 |
25,1 |
42 |
| 50 |
35 |
22,5 |
32,3 |
| 51 |
22 |
31 |
16 |
| 45 |
22,2 |
33 |
32,5 |
| 25 |
20 |
41,9 |
39,3 |
| 33 |
21 |
41,7 |
40,2 |
| 33 |
22 |
37,1 |
0 |
| 39 |
10 |
33,4 |
39,1 |
| 35,8 |
37,4 |
33 |
37,7 |
| 41,7 |
22,4 |
34,3 |
33,5 |
| 38,2 |
35 |
33 |
43,8 |
| 37,4 |
37,3 |
36,9 |
16 |
| 10 |
39,6 |
41 |
16 |
| 37,9 |
0 |
33 |
31 |
| 39,3 |
32,8 |
32,15 |
52 |
| 37,2 |
24 |
38,8 |
51 |
| 37,8 |
25 |
48,1 |
33,5 |
| 49,1 |
38 |
0 |
48 |
| 36,15 |
29 |
0 |
27 |
| 43,8 |
32 |
26,6 |
48 |
| 40 |
32 |
52,8 |
| 40 |
20 |
27 |
| 36 |
32,3 |
13,6 |
| 45 |
10 |
10 |
| 43,5 |
33,9 |
19,5 |
| 35 |
45,74 |
51,2 |
| 35 |
0 |
40,4 |
| 19,5 |
49,1 |
46,05 |
| 24,2 |
38 |
0 |
| 33 |
0 |
25,2 |
| 40,4 |
43,5 |
28 |
| 30 |
32,3 |
27 |
| 36 |
41 |
35 |
| 10 |
40 |
29 |
| 25 |
29,7 |
50 |
| 30 |
30 |
20 |
| 32 |
27,6 |
0 |
| 31 |
21,4 |
15,6 |
| 45 |
23 |
35 |
| 20 |
34,3 |
0 |
| 45 |
18 |
46 |
| 15 |
50,4 |
59,2 |
| 30,4 |
48,2 |
0 |
| 50 |
37,3 |
22,5 |
| 46 |
35 |
0 |
| 35 |
25 |
24 |
| 15 |
20 |
45 |
| 18 |
38 |
28,9 |
| 28 |
47,5 |
30,5 |
| 36,7 |
37,9 |
45,5 |
| 47,8 |
40,3 |
43 |
| 39,2 |
60 |
34,7 |
| 36,5 |
34,1 |
32,6 |
| 32 |
46,7 |
38,4 |
| 45,7 |
39 |
37,15 |
| 46,9 |
31,4 |
39 |
| 15,6 |
32 |
52,15 |
| 34,1 |
42 |
52,2 |
| 44,7 |
43,8 |
0 |
| 26,5 |
39,1 |
0 |
| 36,6 |
16 |
0 |
| 30,3 |
26,5 |
33 |
| 47 |
43 |
43 |
| 50 |
36,9 |
46,6 |
| 52,2 |
29,4 |
59,3 |
| 38,5 |
30,6 |
0 |
| 41 |
35,6 |
15,5 |
| 40 |
38,7 |
21,2 |
| 45 |
38,2 |
22,8 |
| 25,5 |
26,1 |
28,3 |
| 27,7 |
43,2 |
28,15 |
| 22,5 |
46 |
38,5 |
| 45 |
35,6 |
26 |
| 33 |
32,4 |
| 48,3 |
50 |
| 47,5 |
50 |
| 32 |
| 50 |
| 35,6 |
| 33,5 |
| 56,9 |
| 28,9 |
| 40 |
| 35,2 |
| 42,5 |
| 50 |
| 46,2 |
| 52,7 |
| 49,1 |
| 38 |
| 33,7 |
| 32,6 |
| 30 |
| 28,9 |
| 44,4 |
| 48,2 |
| 38,15 |
| 42 |
| 28,4 |
| 33,5 |
| 39,4 |
| 38,6 |
| 34,3 |
| 37,7 |
| 27,3 |
| 39,2 |
| 29,2 |
| 39,2 |
| 33,5 |
| 18 |
| 31,2 |
| 23,4 |
| 36,9 |
| 57,3 |
| 45 |
| 45,3 |
| 16,5 |
| 34,9 |
| 43,1 |
| 30,8 |
| 0 |
| 34,5 |
| 28 |
| 16 |
| 28,9 |
| 23 |
| 27 |
| 41,6 |
| 43,4 |
| 36 |
| 49 |
| 25 |
| 41,5 |
| 35,5 |
| 35 |
| 33,1 |
| 41,7 |
| 39,15 |
| 30,8 |
| 45,7 |
| 35,4 |
| 35,8 |
| 27 |
| 19,5 |
| 29,4 |
| 33,3 |
| 36,6 |
| 42,6 |
| 30 |
| 36,1 |
| 43 |
| 33,3 |
| 28,7 |
| 28,7 |
| 45,1 |
| 31,8 |
| 33 |
| 39,1 |
| 29 |
| 46,7 |
| 41,05 |
| 29,9 |
| 50 |
| 47 |
| 34,4 |
| 11 |
| 20,6 |
| 36,6 |
| 38,6 |
| 29,48 |
| 25 |
| 0 |
| 38 |
| 34,7 |
| 38,2 |
| 43,8 |
| 40,3 |
| 38,5 |
| 60 |
| 50 |
| 36 |
| 55 |
| 33,5 |
| 25,1 |
| 24,8 |
| Всего:Т1
=7502,38 |
Т2
=3157,44 |
Т3
=2819,55 |
Т4
=1223,50 |
Т5
=505,60 |
Т = Т1
+ Т2
+ Т3
+ Т4
+ Т5
Т=15208,47, Т2
= 231297559,74, N = 479
Средние значения выборок:
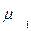 =35,6 =35,6
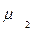 = 31,1 = 31,1
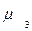 = 28,7 = 28,7
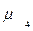 = 26,38 = 26,38
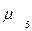 = 19,8 = 19,8
Возведем в квадрат значение всех наблюдений и просуммируем их [6].
Вычисляем:
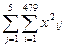 =
567988,11 =
567988,11
Общая сумма квадратов будет следующей:
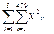 - - 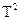 /
N
=
85112,2 /
N
=
85112,2
Находим сумму квадратов между выборками:
(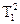 /n1
+….+ /n1
+….+ /nk
) – T2
/N = 8470,35 /nk
) – T2
/N = 8470,35
Теперь можно заполнить таблицу дисперсионного анализа [6].
Таблица №2.
Дисперсионный анализ по одному признаку.
Компонента дисперсии
(1)
|
Сумма квадратов
(2)
|
Степень свободы
(3)
|
Средний квадрат
(4)=(2)/(3)
|
| Между выборками |
(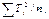 )- )-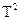 /N /N  |
k-1 |
(определяется делением) |
| Остаточная |
(определяется вычитанием) |
N-k |
| Полная |
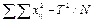 |
N-1 |
----- |
Получаем:
Таблица №2а.
Дисперсионный анализ по одному признаку. Результаты.
Компонента дисперсии
(1)
|
Сумма квадратов
(2)
|
Степень свободы
(3)
|
Средний квадрат
(4)=(2)/(3)
|
| Между выборками |
8470,35 |
4 |
2117,59 |
| Остаточная |
76641,85 |
474 |
161,69 |
| Полная |
85112,2 |
478 |
----- |
Значение критериальной статистики равно:
F = средний квадрат между выборками / остаточный средний квадрат = 2117,59 / 161,69 = 13,09
Сравним F и Fкритич
: 13,09>2,37
Вывод. Следовательно, мы отвергаем гипотезу Н0
,то есть можно предположить, что при 5%-ном уровне значимости УК в крови больных СКВ зависит от степени тяжести поражения почек.
Мы не знаем, какое распределение имеют наши выборки. Описанный метод применяется , как это было описано в статистической модели, для нормальных совокупностей. В связи с этим будет правомочно применить непараметрический метод для выяснения равенства нескольких средних.
2. Непараметрический дисперсионный анализ по одному признаку с применением критерия Краскала-Уоллиса для нескольких независимых выборок
Для проверки совпадений нескольких средних часто применяется непараметрический критерий, свободный от распределения. Его можно использовать, когда рассматриваемые совокупности не являются нормально распределенными [7].
Статистическая модель
Имеется k совокупностей, в нашем случае 5 совокупностей. Каждая выборка извлекается из своей совокупности. Все наблюдения независимы.
Гипотезы
Н0
: все k совокупностей одинаково распределены.
Н1
: нулевая гипотеза не верна.
Критическая область
Верхняя 5%-ная область распределения 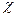 2
k
-1.
В нашем случае
2
k
-1.
В нашем случае 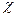 2
4
, что соответствует значению критерия , превышающему 9,49
. Данное число взято из Таблицы А.2 на стр. 331 "Справочника по вычислительным методам статистики" Дж. Полларда. [6]
2
4
, что соответствует значению критерия , превышающему 9,49
. Данное число взято из Таблицы А.2 на стр. 331 "Справочника по вычислительным методам статистики" Дж. Полларда. [6]
Вычисление значения критериальной статистики
Для этого наблюдения xij
заменяются их рангами rij
.Все n наблюдений упорядоченны по возрастанию от 1 до n. Находим сумму рангов R1
, R2
,…, Rk
для k групп. Вычисляем критерий [4]:
H= 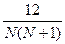 ( R2
1
/n1
+….+ R2
k
/nk
) – 3 ( N + 1 ) ( R2
1
/n1
+….+ R2
k
/nk
) – 3 ( N + 1 )
Значения комплемента упорядочены по возрастанию. Они иногда совпадают, тогда ранг принимает среднее значение.
Далее, используя Таблицу №1
, присваиваем каждому значению комплемента соответствующий ранг в данных пяти выборках и получаем сумму рангов [5] .
Таблица №3.
Таблица рангов наблюдений.
Нет
нефрита
Выборка объема n1
= 210
|
Слабый
нефрит
Выборка объема
n2
= 101
|
Средний
нефрит
Выборка объема
n3
= 98
|
Нефротический синдром
Выборка объема
n4
= 45
|
Почечная недостаточность
Выборка объема
n5
= 25
|
| УК |
Ранг |
УК |
Ранг |
УК |
Ранг |
УК |
Ранг |
УК |
Ранг |
| 36 |
282 |
11 |
45 |
7 |
33 |
10 |
39 |
20 |
86 |
| 38 |
315,5 |
35 |
264 |
27 |
144,5 |
5 |
28,5 |
20 |
86 |
| 40 |
352,5 |
37 |
296,5 |
6 |
31,5 |
6 |
31,5 |
21 |
95,5 |
| 31 |
188,5 |
15 |
59,5 |
5 |
28,5 |
15 |
59,5 |
24 |
115 |
| 33 |
220 |
40 |
352,5 |
40 |
352,5 |
20 |
86 |
3 |
26 |
| 33,8 |
242 |
0 |
13 |
5 |
28,5 |
25 |
126,5 |
12 |
50 |
| 37 |
296,5 |
33 |
220 |
45 |
405,5 |
28 |
28 |
10 |
39 |
| 38 |
315,5 |
33 |
220 |
45 |
405,5 |
32 |
197,5 |
0 |
13 |
| 33 |
220 |
5 |
28,5 |
46 |
420,5 |
46 |
420,5 |
18,2 |
77 |
| 37 |
296,5 |
40 |
352,5 |
45 |
405,5 |
33 |
220 |
46 |
420,5 |
| 48 |
436,5 |
25 |
126,5 |
24 |
115 |
44 |
396,5 |
10 |
39 |
| 40 |
352,5 |
33 |
220 |
24 |
115 |
25 |
126,5 |
0 |
13 |
| 42 |
375,5 |
50 |
453,5 |
43 |
383 |
22,5 |
105,5 |
20 |
86 |
| 35 |
264 |
25 |
126,5 |
24,5 |
119,5 |
24,5 |
119,5 |
30,4 |
181,5 |
| 15 |
59,5 |
20 |
86 |
20,5 |
92 |
38 |
315,5 |
0 |
13 |
| 35 |
264 |
50 |
453,5 |
9 |
34 |
12 |
50 |
33,3 |
231 |
| 48 |
436,5 |
50 |
453,5 |
12 |
50 |
54,7 |
471 |
14,7 |
56 |
| 45 |
405,5 |
18 |
74,5 |
32 |
197,5 |
20,7 |
94 |
34,1 |
247 |
| 38 |
315,5 |
20 |
86 |
43 |
383 |
0 |
13 |
22,4 |
102,5 |
| 15 |
59,5 |
33 |
220 |
35,5 |
273,5 |
26,1 |
137,5 |
17,8 |
72 |
| 13 |
53 |
43 |
383 |
44 |
396,5 |
11 |
45 |
33,5 |
237 |
| 40 |
352,5 |
10 |
39 |
50 |
453,5 |
11,7 |
47 |
29,6 |
171 |
| 40 |
352,5 |
12 |
50 |
34 |
244,5 |
34,4 |
252,5 |
13,6 |
54,5 |
| 38 |
315,5 |
23 |
110 |
12 |
50 |
0 |
13 |
35 |
264 |
| 32,7 |
210 |
34 |
244,5 |
0 |
13 |
0 |
13 |
37 |
296,5 |
| 60 |
478 |
30 |
176,5 |
25,1 |
132,5 |
42 |
375,5 |
| 50 |
453,5 |
35 |
264 |
22,5 |
105,5 |
32,3 |
204 |
| 51 |
462,5 |
22 |
99,5 |
31 |
188,5 |
16 |
68 |
| 45 |
405,5 |
22,2 |
101 |
33 |
220 |
32,5 |
207 |
| 25 |
26,5 |
20 |
86 |
41,9 |
373 |
39,3 |
345,5 |
| 33 |
220 |
21 |
95,5 |
41,7 |
371 |
40,2 |
359 |
| 33 |
220 |
22 |
99,5 |
37,1 |
299 |
0 |
13 |
| 39 |
334 |
10 |
39 |
33,4 |
233 |
39,1 |
337 |
| 35,8 |
278,5 |
37,4 |
304,5 |
33 |
220 |
37,7 |
306,5 |
| 41,7 |
371 |
22,4 |
102,5 |
34,3 |
250 |
33,5 |
237 |
| 38,2 |
323 |
35 |
264 |
33 |
220 |
43,8 |
393,5 |
| 37,4 |
304,5 |
37,3 |
302,5 |
36,9 |
293 |
16 |
68 |
| 10 |
39 |
39,6 |
346 |
41 |
365 |
16 |
68 |
| 37,9 |
309,5 |
0 |
13 |
33 |
220 |
31 |
188,5 |
| 39,3 |
343,5 |
32,8 |
211 |
32,15 |
202 |
52 |
465 |
| 37,2 |
301 |
24 |
115 |
38,8 |
332 |
51 |
462,5 |
| 37,8 |
308 |
25 |
126,5 |
48,1 |
439 |
33,5 |
237 |
| 49,1 |
445 |
38 |
315,5 |
0 |
13 |
48 |
436,5 |
| 36,15 |
286 |
29 |
165 |
0 |
13 |
27 |
144,5 |
| 43,8 |
393,5 |
32 |
197,5 |
26,6 |
141 |
48 |
436,5 |
| 40 |
352,5 |
32 |
197,5 |
52,8 |
470 |
| 40 |
352,5 |
20 |
86 |
27 |
144,5 |
| 36 |
282 |
32,3 |
204 |
13,6 |
54,5 |
| 45 |
405,5 |
10 |
39 |
10 |
39 |
| 43,5 |
390,5 |
33,9 |
243 |
19,5 |
79 |
| 35 |
264 |
45,74 |
417 |
51,2 |
464 |
| 35 |
264 |
0 |
13 |
40,4 |
362,5 |
| 19,5 |
79 |
49,1 |
445 |
46,05 |
424 |
| 24,2 |
118 |
38 |
315,5 |
0 |
13 |
| 33 |
220 |
0 |
13 |
25,2 |
134 |
| 40,4 |
362,5 |
43,5 |
390,5 |
28 |
152,5 |
| 30 |
176,5 |
32,3 |
204 |
27 |
144,5 |
| 36 |
282 |
41 |
365 |
35 |
264 |
| 10 |
39 |
40 |
352,5 |
29 |
165 |
| 25 |
126,5 |
29,7 |
172 |
50 |
453,5 |
| 30 |
176,5 |
30 |
176,5 |
20 |
86 |
| 32 |
197,5 |
27,6 |
149 |
0 |
13 |
| 31 |
188,5 |
21,4 |
98 |
15,6 |
64,5 |
| 45 |
405,5 |
23 |
110 |
35 |
264 |
| 20 |
86 |
34,3 |
250 |
0 |
13 |
| 45 |
405,5 |
18 |
74,5 |
46 |
425 |
| 15 |
59,5 |
50,4 |
461 |
59,2 |
475 |
| 30,4 |
181,5 |
48,2 |
440,5 |
0 |
13 |
| 50 |
453,5 |
37,3 |
302,5 |
22,5 |
105,5 |
| 46 |
420,5 |
35 |
264 |
0 |
13 |
| 35 |
264 |
25 |
126,5 |
24 |
115 |
| 15 |
59,5 |
20 |
86 |
45 |
405,5 |
| 18 |
74,5 |
38 |
315,5 |
28,9 |
161,5 |
| 28 |
152,5 |
47,5 |
432,5 |
30,5 |
183 |
| 36,7 |
291 |
37,9 |
309,5 |
45,5 |
414 |
| 47,8 |
434 |
40,3 |
360,5 |
43 |
383 |
| 39,2 |
341 |
60 |
478 |
34,7 |
255,5 |
| 36,5 |
287 |
34,1 |
247 |
32,6 |
208,5 |
| 32 |
197,5 |
46,7 |
427,5 |
38,4 |
325 |
| 45,7 |
415,5 |
39 |
334 |
37,15 |
300 |
| 46,9 |
429 |
31,4 |
192 |
39 |
334 |
| 15,6 |
64,5 |
32 |
197,5 |
52,15 |
466 |
| 34,1 |
247 |
42 |
375,5 |
52,2 |
467,5 |
| 44,7 |
399 |
43,8 |
393,5 |
0 |
13 |
| 26,5 |
139,5 |
39,1 |
337 |
0 |
13 |
| 36,6 |
289 |
16 |
68 |
0 |
13 |
| 30,3 |
180 |
26,5 |
139,5 |
33 |
220 |
| 47 |
430,5 |
43 |
383 |
43 |
383 |
| 50 |
453,5 |
36,9 |
293 |
46,6 |
426 |
| 52,2 |
467,5 |
29,4 |
168,5 |
59,3 |
476 |
| 38,5 |
327 |
30,6 |
184 |
0 |
13 |
| 41 |
365 |
35,6 |
276 |
15,5 |
63 |
| 40 |
352,5 |
38,7 |
331 |
21,2 |
97 |
| 45 |
405,5 |
38,2 |
323 |
22,8 |
108 |
| 25,5 |
135 |
26,1 |
137,5 |
28,3 |
156 |
| 27,7 |
150 |
43,2 |
388 |
28,15 |
155 |
| 22,5 |
46 |
420,5 |
38,5 |
327 |
| 45 |
105,5 |
35,6 |
276 |
26 |
136 |
| 33 |
220 |
32,4 |
206 |
| 48,3 |
442 |
50 |
453,5 |
| 47,5 |
432,5 |
50 |
453,5 |
| 32 |
197,5 |
| 50 |
453,5 |
| 35,6 |
276 |
| 33,5 |
237 |
| 56,9 |
473 |
| 28,9 |
161,5 |
| 40 |
352,5 |
| 35,2 |
271 |
| 42,5 |
378 |
| 50 |
453,5 |
| 46,2 |
425 |
| 52,7 |
469 |
| 49,1 |
445 |
| 38 |
315,5 |
| 33,7 |
241 |
| 32,6 |
208,5 |
| 30 |
176,5 |
| 28,9 |
161,5 |
| 44,4 |
398 |
| 48,2 |
440,5 |
| 38,15 |
321 |
| 42 |
375,5 |
| 28,4 |
157 |
| 33,5 |
237 |
| 39,4 |
345 |
| 38,6 |
329,5 |
| 34,3 |
250 |
| 37,7 |
306,5 |
| 27,3 |
148 |
| 39,2 |
341 |
| 29,2 |
167 |
| 39,2 |
341 |
| 33,5 |
237 |
| 18 |
74,5 |
| 31,2 |
191 |
| 23,4 |
112 |
| 36,9 |
293 |
| 57,3 |
474 |
| 45 |
405,5 |
| 45,3 |
413 |
| 16,5 |
71 |
| 34,9 |
257 |
| 43,1 |
387 |
| 30,8 |
185,5 |
| 0 |
13 |
| 34,5 |
254 |
| 28 |
152,5 |
| 16 |
68 |
| 28,9 |
161,5 |
| 23 |
110 |
| 27 |
144,5 |
| 41,6 |
369 |
| 43,4 |
389 |
| 36 |
282 |
| 49 |
443 |
| 25 |
126,5 |
| 41,5 |
368 |
| 35,5 |
273,5 |
| 35 |
264 |
| 33,1 |
229 |
| 41,7 |
371 |
| 39,15 |
339 |
| 30,8 |
185,5 |
| 45,7 |
415,5 |
| 35,4 |
272 |
| 35,8 |
278,5 |
| 27 |
144,5 |
| 19,5 |
79 |
| 29,4 |
168,5 |
| 33,3 |
231 |
| 36,6 |
289 |
| 42,6 |
379 |
| 30 |
176,5 |
| 36,1 |
285 |
| 43 |
383 |
| 33,3 |
231 |
| 28,7 |
158,5 |
| 28,7 |
158,5 |
| 45,1 |
412 |
| 31,8 |
193 |
| 33 |
220 |
| 39,1 |
337 |
| 29 |
165 |
| 46,7 |
427,5 |
| 41,05 |
367 |
| 29,9 |
173 |
| 50 |
453,5 |
| 47 |
430,5 |
| 34,4 |
252,5 |
| 11 |
45 |
| 20,6 |
93 |
| 36,6 |
289 |
| 38,6 |
289 |
| 29,48 |
170 |
| 25 |
126,5 |
| 0 |
13 |
| 38 |
315,5 |
| 34,7 |
255,5 |
| 38,2 |
323 |
| 43,8 |
393,5 |
| 40,3 |
360,5 |
| 38,5 |
327 |
| 60 |
478 |
| 50 |
453,5 |
| 36 |
282 |
| 55 |
472 |
| 33,5 |
237 |
| 25,1 |
132,5 |
| 24,8 |
121 |
| Всего: |
R1
=
57877
|
R2
=
23298.5
|
R3
=
21259.5
|
R4
=
8789
|
R5
=
3072
|
| N = 479 |
k = 5 |
| R1
= 57877 |
n1
= 210 |
| R2
= 23298,5 |
n2
= 101 |
| R3
= 21259,5 |
n3
= 98 |
| R4
= 8789 |
n4
= 45 |
| R5
= 3072 |
n5
= 25 |
Теперь можно полученные суммы рангов подставить в формулу и получить значение критериальной статистики Краскела-Уоллиса [4] :
Н=23,03
Полученный результат не является незначимым, поэтому нельзя считать, что выборки извлечены из одинаково распределенных совокупностей и что средние значения совокупностей совпадают. Но этот вывод является приближенным, так как в нашей таблице есть много совпадающих значений. Для учета влияния связей можно воспользоваться модифицированной формой статистики Краскела-Уоллиса [4]:
Н`
= 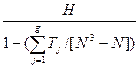
, где g – число групп совпадающих значений, Тj
= (t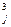 - t - t ), t ), t – число совпадающих наблюдений в группе с номером j . – число совпадающих наблюдений в группе с номером j .
Таблица №4.
Группы совпадающих наблюдений.
| Повторяющиеся значения УК |
Кол-во повторений tj
|
Значение Tj
|
| 0 |
25 |
15600 |
| 5 |
4 |
60 |
| 6 |
2 |
6 |
| 10 |
9 |
720 |
| 11 |
3 |
24 |
| 12 |
5 |
120 |
| 13,6 |
2 |
6 |
| 15 |
6 |
210 |
| 15,6 |
2 |
6 |
| 16 |
5 |
120 |
| 18 |
4 |
60 |
| 19,5 |
3 |
24 |
| 20 |
11 |
1320 |
| 21 |
2 |
6 |
| 22 |
2 |
6 |
| 22,4 |
2 |
6 |
| 22,5 |
4 |
60 |
| 23 |
3 |
24 |
| 24 |
5 |
120 |
| 24,5 |
2 |
6 |
| 25 |
10 |
990 |
| 25,1 |
2 |
6 |
| 26,1 |
2 |
6 |
| 26,5 |
2 |
6 |
| 27 |
6 |
210 |
| 28 |
4 |
60 |
| 28,7 |
2 |
6 |
| 28,9 |
4 |
60 |
| 29 |
3 |
24 |
| 29,4 |
2 |
6 |
| 30 |
6 |
210 |
| 30,4 |
2 |
6 |
| 30,8 |
2 |
6 |
| 31 |
4 |
60 |
| 32 |
8 |
504 |
| 32,3 |
3 |
24 |
| 32,6 |
2 |
6 |
| 33 |
17 |
4896 |
| 33,3 |
3 |
24 |
| 33,5 |
7 |
336 |
| 34 |
2 |
6 |
| 34,1 |
3 |
24 |
| 34,3 |
3 |
24 |
| 34,4 |
2 |
6 |
| 34,7 |
2 |
6 |
| 35 |
13 |
2184 |
| 35,5 |
2 |
6 |
| 35,6 |
3 |
24 |
| 35,8 |
2 |
6 |
| 36 |
5 |
120 |
| 36,6 |
3 |
24 |
| 36,9 |
3 |
24 |
| 37 |
4 |
60 |
| 37,3 |
2 |
6 |
| 37,4 |
2 |
6 |
| 37,7 |
2 |
6 |
| 37,9 |
2 |
6 |
| 38 |
10 |
990 |
| 38,2 |
3 |
24 |
| 38,5 |
3 |
24 |
| 38,6 |
2 |
6 |
| 39 |
3 |
24 |
| 39,1 |
3 |
24 |
| 39,2 |
3 |
24 |
| 39,3 |
2 |
6 |
| 40 |
12 |
1716 |
| 40,3 |
2 |
6 |
| 40,4 |
2 |
6 |
| 41 |
3 |
24 |
| 41,7 |
3 |
24 |
| 42 |
4 |
60 |
| 43 |
7 |
336 |
| 43,5 |
2 |
6 |
| 43,8 |
4 |
60 |
| 44 |
2 |
6 |
| 45 |
12 |
1716 |
| 45,7 |
2 |
6 |
| 46 |
6 |
210 |
| 46,7 |
2 |
6 |
| 47 |
2 |
6 |
| 47,5 |
2 |
6 |
| 48 |
4 |
60 |
| 48,2 |
2 |
6 |
| 49,1 |
3 |
24 |
| 50 |
14 |
2730 |
| 51 |
2 |
6 |
| 52,2 |
2 |
6 |
| 60 |
3 |
24 |
g = 88
Теперь можно полученные результаты подставить в модифицированную формулу и получить уточненное значение критериальной статистики Краскела-Уоллиса :
Н`
= 23,037
Вывод.
Скорректированное значение Н`
статистики Краскела-Уоллиса несущественно отличается от значения Н, т.о. мы можем отвергнуть гипотезу Н0
на минимальном уровне значимости. Следовательно , мы подтвердили результат полученный ранее : существует зависимость между УК в крови больных СКВ и степенью тяжести поражения почек .
3. Непараметрический дисперсионный анализ по одному признаку с применением критерия Джонкхиера для нескольких выборок, упорядоченных по возрастанию влияния фактора
Нам заранее известно, что имеющиеся группы результатов упорядочены по возрастанию влияния фактора.. В нашем случае фактором является степень тяжести ГН. В таких случаях целесообразно использовать критерий Джонхиера , более чувствительный против альтернатив об упорядоченном влиянии фактора [5].
Статистическая модель
Имеется k совокупностей, в нашем случае 5 совокупностей. Каждая выборка извлекается из своей совокупности. Все наблюдения независимы. имеющиеся группы результатов упорядочены по возрастанию влияния фактора 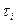 . 1-й столбец Таблицы №1 отвечает наименьшему уровню фактора, последний – наибольшему, а промежуточные столбцы получили номера, соответствующие их положению. В нашем случае фактором является степень тяжести поражения почек [4] . . 1-й столбец Таблицы №1 отвечает наименьшему уровню фактора, последний – наибольшему, а промежуточные столбцы получили номера, соответствующие их положению. В нашем случае фактором является степень тяжести поражения почек [4] .
Гипотезы
Н0
: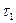 = =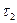 =…= =…=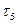 ( влияние фактора упорядоченно.) ( влияние фактора упорядоченно.)
Н1
: 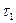 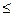 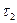 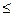 … …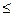 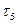
Критическая область
Верхняя 5% область F-распределения, что в нашем случае соответствует значению критерия, превышающему значение 2,21. Данное число взято из таблицы А.4 на стр. 334 [6].
Вычисление значения критериальной статистики
Вычислим статистику Манна – Уитни. Сравниваем k способов обработки, в нашем случае 5. Поступим следующим образом : для каждой пары натуральных чисел u и v , где 1£u<v£k , составляем по выборкам с номерами u,vстатистику Манна – Уитни [4].
U = 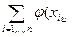 , y , y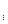 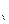 ) )
Определим так же статистику Джонхиера как :
J = 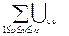
Для нахождения значений статистики Манна – Уитни будем использовать программу,( так как мы имеем выборки большого объема) написанную на языке FortranPowerStation для Windows , версия 4.0 .Выбор данного языка программирования связан с тем, что он максимально приближен к общепринятому языку математических формул. [11].
implicit real*8 (a-h, o-z)
dimension a1(210), a2(101),a3(98),a4(45),a5(25)
open (unit=11, file='1.dat', access='sequential', status='old')
open (unit=12, file='2.dat', access='sequential', status='old')
open (unit=13, file='3.dat', access='sequential', status='old')
open (unit=14, file='4.dat', access='sequential', status='old')
open (unit=15, file='5.dat', access='sequential', status='old')
open (unit=16, file='res.dat',access='append',status='unknown')
do 2222 i=1,210
read (11, 21) a1(i)
21 format(e8.1)
2222 continue
do 2223 i=1,101
read (12, 21) a2(i)
2223 continue
do 2224 i=1,98
read (13, 21) a3(i)
2224 continue
do 2225 i=1,45
read (14, 21) a4(i)
2225 continue
do 2226 i=1,25
read (15, 21) a5(i)
2226 continue
u12=0
do 101 i=1,210
do 91 j=1,101
if (a1(i)<a2(j)) then
u12 = u12+1
elseif (a1(i).eq.a2(j)) then
u12= u12+0.5
else
u12= u12+0.0
endif
91 continue
101 continue
u13=0
do 102 i=1,210
do 92 j=1,98
if (a1(i)<a3(j)) then
u13 = u13+1
elseif (a1(i).eq.a3(j)) then
u13= u13+0.5
else
u13= u13+0.0
endif
92 continue
102 continue
u14=0
do 103 i=1,210
do 93 j=1,45
if (a1(i)<a4(j)) then
u14 = u14+1
elseif (a1(i).eq.a4(j)) then
u14= u14+0.5
else
u14= u14+0.0
endif
93 continue
103 continue
u15=0
do 104 i=1,210
do 94 j=1,25
if (a1(i)<a5(j)) then
u15 = u15+1
elseif (a1(i).eq.a5(j)) then
u15= u15+0.5
else
u15= u15+0.0
endif
94 continue
104 continue
u23=0
do 105 i=1,101
do 95 j=1,98
if (a2(i)<a3(j)) then
u23 = u23+1
elseif (a2(i).eq.a3(j)) then
u23= u23+0.5
else
u23= u23+0.0
endif
95 continue
105 continue
u24=0
do 106 i=1,101
do 96 j=1,45
if (a2(i)<a4(j)) then
u24 = u24+1
elseif (a2(i).eq.a4(j)) then
u24= u24+0.5
else
u24= u24+0.0
endif
96 continue
106 continue
u25=0
do 107 i=1,101
do 97 j=1,25
if (a2(i)<a5(j)) then
u25 = u25+1
elseif (a2(i).eq.a5(j)) then
u25= u25+0.5
else
u25= u25+0.0
endif
97 continue
107 continue
u34=0
do 108 i=1,98
do 98 j=1,45
if (a3(i)<a4(j)) then
u34 = u34+1
elseif (a3(i).eq.a4(j)) then
u34= u34+0.5
else
u34= u34+0.0
endif
98 continue
108 continue
u35=0
do 109 i=1,98
do 99 j=1,25
if (a3(i)<a5(j)) then
u35 = u35+1
elseif (a3(i).eq.a5(j)) then
u35= u35+0.5
else
u35= u35+0.0
endif
99 continue
109 continue
u45=0
do 110 i=1,45
do 100 j=1,25
if (a4(i)<a5(j)) then
u45 = u45+1
elseif (a4(i).eq.a5(j)) then
u45= u45+0.5
else
u45= u45+0.0
endif
100 continue
110 continue
U=u12+u13+u14+u15+u23+u24+u25+u34+u35+u45
22 format(2x,'u12=',f10.3)
23 format(2x,'u13=',f10.3)
24 format(2x,'u14=',f10.3)
25 format(2x,'u15=',f10.3)
26 format(2x,'u23=',f10.3)
27 format(2x,'u24=',f10.3)
28 format(2x,'u25=',f10.3)
29 format(2x,'u34=',f10.3)
30 format(2x,'u35=',f10.3)
31 format(2x,'u45=',f10.3)
32 format(2x,'U=',f10.3)
write(16,22)u12
write(16,23)u13
write(16,24)u14
write(16,25)u15
write(16,26)u23
write(16,27)u24
write(16,28)u25
write(16,29)u34
write(16,30)u35
write(16,31)u45
write(16,32)U
end
Обработав таким образом результаты наблюдений, получаем значения статистики Манна – Уитни:
 u12= 8441,000 u12= 8441,000
u13= 7793,500
u14= 3172,500
u15= 888,000
u23= 4637,500
u24= 1928,500
u25= 648,500
u34= 2054,500
u35= 805,500
u45= 411,000
Подставив в формулу полученные значения получаем результат для статистики Джонхиера:
J= 30780,5
Значение статистики Джонхиера очень велико, что свидетельствует в пользу гипотезы Н1
об упорядоченном влиянии фактора , в нашем случае – зависимости УК в крови больных СКВ от степени поражения почек. То есть мы снова подтвердили результат, полученный ранее.
Но поскольку предложенные выборки велики, то можно проверить полученный результат, подсчитав приближенную статистику J* для большой выборки [4].
Вычислим величину:
J*
= ( J – MJ ) /  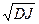
Где MJ = 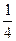 ( N2
- ( N2
- 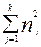 ) , DJ = ) , DJ = 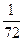 ( N2
( 2N + 3 ) - ( N2
( 2N + 3 ) - 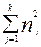 ( 2nj
+ 3)) ( 2nj
+ 3))
В результате вычислений мы получаем значение J*
= 5,9.
Вывод.
Полученный результат превышает критическое значение, что позволяет отклонить гипотезу Н0
, и принять гипотезу Н1.
Таким образом мы подтверждается результат, полученный с помощью статистики J – влияние фактора в предложенных выборках упорядоченно.
§4.Вывод
Целью данной курсовой работы был анализ зависимости между УК в крови больных СКВ и степенью тяжести поражения почек. Исходные данные были подвергнуты методам статистического анализа, независимым между собой. Результатом является доказательство наличия зависимости УК в крови больных СКВ и степенью тяжести поражения почек в каждом из использованных методов, что позволяет сформулировать окончательный вывод : УК в крови больных СКВ зависит от степени тяжести поражения почек, причем УК уменьшается с возрастанием степени тяжести поражения почек.
§5. Список литературы
1. Гублер Е.В. Информатика в патологии, клинической медицине и педиатрии. –Л.: Медицина, 1990.-176с.
2. Кузин Ф.А. Кандидатская диссертация . Методика написания, правила оформления и порядок защиты. Практическое пособие для аспирантов и соискателей ученой степени. –5-е изд., доп.-М.:Ось 89, 2000.-224с.
3. Энциклопедический словарь медицинских терминов: В 3-х томах. Около 60000 терминов.-М.: Советская энциклопедия, - Т.2. 1983.-448с.
4. Тюрин Ю.Н. , Макаров А.А. Статистический анализ данных на компьютере .-М.: Инфра – М., 1982.-528с.
5. Холлендер М., Вулф Д.А. Непараметрические методы статистики.-М.: Финансы и статистика., 1983.-518с.
6. Поллард Дж. Справочник по вычислительным методам статистики.-М.: Финансы и статистика., 1982.-344с.
7. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Исследование зависимостей.-М.: Финансы и статистика,-Т.2. 1985.-488с.
8. Шишкин В.И., Кудрявцева Г.В. Регуляторная роль функциональной системы "Комплемент – простагландиды – пентозофосфатный путь обмена углеводов" в патогенезе основных ревматологических заболеваний.-СПб.: НИИХ. 2002.-38с.
9. Колмогоров А.Н. Теория вероятности и математическая статистика.-М.:Наука.,1986.-535с.
10. Фишер Р.А. Статистические методы для исследователей.-М.:Госстатиздат.,1982.-344с.
11. Фишер Ф.П., Суиндл Д.Ф. Системы программирования.-М.:Статистика.,1971.-606с.
|