ФИНАНСОВАЯ АКАДЕМИЯ ПРИ ПРАВИТЕЛЬСТВЕ РФ

КАФЕДРА МТЕМАТИКИ

КУРСОВАЯ РАБОТА

тема:

Применение метода ветвей и границ для задач календарного планирования

Студент группы МЭК 1-1 Клеймёнов И.Д.

Научный руководитель Солодовников А.С.

МОСКВА, 2001г.

План

1.Постановка задачи целочисленного программирования. 3

2. Понятие о методе ветвей и границ. 4

3.Применение метода ветвей и границ для задач календарного планирования. 13

Летература. 20

1.Постановка задачи целочисленного программирования

По смыслу значительной части экономических задач, относятся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.

Задача линейного целочисленного программирования формируется следующим образом: найти такое решение (план) X = (x₁ ,x₂ ,...,x_n ), при котором линейная функция

(1)

принимает максимальное или минимальное значение при ограничениях

=b _i , i= 1, 2…, m. (2)

х_j ³ 0,j =1,2,..., п. (3)

x_j — целые числа (4)

2. Понятие о методе ветвей и границ

Метод ветвей и границ — один из комбинаторных методов. Его суть заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.

Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор, пока не получено оптимальное целочисленное решение исходной задачи.

Алгоритм решения:

Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Пусть им является план X₀ . Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи и F_max = F(X_o ).

Если же среди компонент плана X₀ имеются дробные числа, то X₀ не удовлетворяет условию целочисленности и необходимо осуществить упорядоченный переход к новым планам, пока не будет найдено решение задачи. Покажем, как это можно сделать, предварительно отметив, что F(X₀ ) ³F(X)для всякого последующего плана X.

Предполагая, что найденный оптимальный план X₀ не удовлетворяет условию целочисленности переменных, тем самым считаем, что среди его компонент есть дробные числа. Пусть, например, переменная приняла в плане X₀ дробное значение. Тогда в оптимальном целочисленном плане ее значение будет по крайней мере либо меньше или равно ближайшему меньшему целому числу, либо больше или равно ближайшему большему целому числу + 1. Определяя эти числа, находим симплексным методом решение двух задач линейного программирования:

Найдем решение задач линейного программирования (I) и (II). Очевидно, здесь возможен один из следующих четырех случаев:

1. Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции на нем и дают решение исходной задачи.

2. Одна из задач неразрешима, а другая имеет оптимальный план, среди компонент которого есть дробные числа. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу, и строим две задачи, аналогичные задачам (I) и (II).

3. Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции на этих планах и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и он вместе со значением целевой функции на нем дает искомое решение.

Если же значение целевой функции больше на плане, среди компонент которого есть дробные числа, то следует взять одно из таких чисел и для задачи, план которой рассматривается, необходимо построить две задачи, аналогичные (I) и (II).

4. Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда вычисляем значение целевой функции на данных оптимальных планах и рассматриваем ту из задач, для которой значение целевой функции является наибольшим. В оптимальном плане этой задачи выбираем одну из компонент, значение которой является дробным числом, и строим две задачи, аналогичные (I) и (II).

Таким образом, описанный выше итерационный процесс может быть представлен в виде некоторого дерева, на котором исходная вершина отвечает оптимальному плану Х₀ задачи (1)-(3), а каждая соединенная с ней ветвью вершина отвечает оптимальным планам задач (I) и (II). Каждая из этих вершин имеет свои ветвления. При этом на каждом шаге выбирается та вершина, для которой значение функции является наибольшим. Если на некотором шаге будет получен план, имеющий целочисленные компоненты, и значение функции на нем окажется больше или равно, чем значение функции в других возможных для ветвления вершинах, то данный план является оптимальным планом исходной задачи целочисленного программирования и значение целевой функции на нем является максимальным.

Итак, процесс нахождения решения задачи целочисленного программирования (1)-(4) методом ветвей и границ включает следующие основные этапы:

1°. Находят решение задачи линейного программирования (1)-(3).

2°. Составляют дополнительные ограничения для одной из пере-менных, значение которой в оптимальном плане задачи (1)-(3) является дробным числом.

3°. Находят решение задач (I) и (II), которые получаются из задачи (1)-(3) в результате присоединения дополнительных ограничений.

4°. В случае необходимости составляют дополнительные ограничения для переменной, значение которой является дробным, формулируют задачи, аналогичные задачам (I) и (II), и находят их решение. Итерационный процесс продолжают до тех пор, пока не будет найдена вершина, соответствующая целочисленному плану задачи (1)-(3) и такая, что значение функции в этой вершине больше или равно значению функции в других возможных для ветвления вершинах.

Описанный выше метод ветвей и границ имеет более простую логическую схему расчетов, чем метод Гомори. Поэтому в большинстве случаев для нахождения решения конкретных задач целочисленного программирования с использованием ЭВМ применяется именно этот метод.

Проиллюстрируем метод ветвей и границ на примере.

Решить задачу

Z = Зх₁ + х₂ — max

при ограничениях:

4x_l + Зх₂ < 18,

x₁ + 2x₂ £ 6,

0 £x₁ £ 5,

0 £x₂ £ 4,

х₁ , x₂ — целые числа.

Решение. За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т.е. Z₀ = Z (0; 0) = 0.

I этап. Решая задачу симплексным методом, получим Z_max = 13 при Х₁ ^* = (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента х₁ ^* дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение х₁ ^* , т.е. 4 < х₁ < 5. Поэтому задача 1 разбивается на две задачи 2 и 3:

Задача 2

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

0 £x₁ £ 4

0 £x₂ £ 4

х₁ , x₂ — целые числа.

Задача 3

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

5 £x₁ £ 5

0 £x₂ £ 4

х₁ , x₂ — целые числа.

Список задач: 2 и 3. Нижняя граница линейной функции не изменилась: Z₀ = 0.

II этап. Решаем (по выбору) одну из задач списка, например задачу 3 симплексным методом.

Получим, что условия задачи 3 противоречивы.

III этап. Решаем задачу 2 симплексным методом. Получим Z_max = 14/3 при X₃ ^* = (4; 2/3; 0; 2/3; 0; 10/3). Хотя Z(X₃ ^* ) = 14/3 > Z₀ = 0, по-прежнему сохраняется Z₀ = 0, ибо план нецелочисленный. Так как х₂ ^* — дробное число, из области решений исключаем полосу 0 < x₂ < 1 и задачу 2 разбиваем на две задачи 4 и 5.

Задача 4

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

0 £x₁ £ 4

0 £x₂ £0

х₁ , x₂ — целые числа.

Задача 5

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

0£x₁ £4

1£x₂ £ 4

х₁ , x₂ — целые числа.

Список задач: 4 и 5. Значение Z₀ = 0.

IV этап. Решаем задачу 4 симплексным методом.

Получим Z_max = 12 при X₄ ^* = (4; 0; 2; 2; 0; 0). Задачу исключаем из списка, но при этом меняем Z₀ ; Z₀ = Z(X₄ ^* ) = 12, ибо план Х₄ ^* целочисленный.

V этап. Решаем задачу 5 симплексным методом.

Получим Z_max = 12,25 при X₅ ^* = (3,75; 1; 0; 0,25; 0,25; 0; 3). Z ₀ не меняется, т.е. Z₀ = 12, ибо план X₅ ^* нецелочисленный. Так как х₁ ^* — дробное, из области решений исключаем полосу 3<x₁ <4, и задача 5 разбивается на две задачи: 6 и 7.

Задача 6

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

0 £x₁ £ 3

1 £x₂ £ 4

х₁ , x₂ — целые числа.

Задача 7

Z=3x₁ +x₂ →max

при ограничениях:

4x_l + Зх₂ < 18

x₁ + 2x₂ £ 6

4 £x₁ £ 4

1 £x₂ £ 4

х₁ , x₂ — целые числа.

Список задач: 6 и 7. Значение Z₀ = 12.

VI этап. Решаем одну из задач списка, например задачу 7, симплексным методом.

Получим, что условия задачи 7 противоречивы.

VII этап. Решаем задачу 6 симплексным методом.

Получим Z_{m ax} = 10,5 ,при X₆ ^* = (3; 1,5; 1,5; 0; 0; 0,5; 2,5).

Так какZ(X₆ ^* ) = 10,5 < Z₀ = 12, то задача исключается из списка.

Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет X^* = Х₄ ^* = (4; 0; 2; 2; 0; 0), а оптимум линейной функции Z_max = 12

Замечание 1. Нетрудно видеть, что каждая последующая задача, составляемая в процессе применения метода ветвей и границ, отличается от предыдущей лишь одним неравенством — ограничением. Поэтому при решении каждой последующей задачи нет смысла решать ее симплексным методом с самого начала (с I шага). А целесообразнее начать решение с последнего шага (итерации) предыдущей задачи, из системы ограничений которой исключить "старые" (одно или два) уравнения — ограничения и ввести в эту систему "новые" уравнения — ограничения.

3.Применение метода ветвей и границ для задач календарного планирования

Метод ветвей и границ является универсальным методом решения комбинаторных задач дискретного программирования. Сложность практического применения метода заключается в трудностях нахождения способа ветвления множества на подмножества и вычисления соответствующих оценок, которые зависят от специфики конкретной задачи.

Рассмотрим применение разновидности метода ветвей и границ— метода «последовательного конструирования и анализа вариантов» для решения задачи календарного планирования трех станков.

Заданы п деталей d_i ( i = 1, 2, ..., n ), последовательно обрабатываемых на трех станках R ₁ , R ₂ , R ₃ , причем технологические маршруты всех деталей одинаковы. Обозначим a_i , b_i , c_i — длительность обработки деталей d_i на первом, втором и третьем станках соответственно.

Определить такую очередность запуска деталей в обработку, при которой минимизируется суммарное время завершения всех работ T_ц .

Можно показать, что в задаче трех станков очередность выполнения первых, вторых и третьих операций в оптимальном решении может быть одинаковой (для четырех станков это свойство уже не выполняется). Поэтому достаточно определить очередность запуска только на одном станке (например, третьем).

Обозначим s_k = ( i ₁ , i ₂ , ..., i_k ) — некоторую последовательность очередности запуска длиной k (1 £k £ п) и A (s_k ), В ( s_k ), С ( s_k ) — время окончания обработки последовательности деталей s_k на первом, втором и третьем станках соответственно.

Необходимо найти такую последовательность s_опт , что

С(s_опт ) = min С (s).

s

Покажем, как можно рекуррентно вычислять A (s_k ), В ( s_k ), С ( s_k ) . Пусть s_{k +1} = ( s _k , i _{k + i} ), т. е. последовательность деталей s_{k +1} получена из деталей s_k с добавлением еще одной детали i _{k +1} . Тогда

A ( s_k+1 ) = A ( s_k )+,

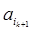В (s_k+1 ) = max [A (s_k+1 ); В (s_k )]+ ,

С (s_{k +1} ) = max [В (s_{k +1} ); С (s_k )] +

Для задачи трех станков можно использовать следующее правило доминирования .

Если s— некоторая начальная последовательность, а — под последовательность образованная из s перестановкой некоторых символов, то вариант s доминирует над , когда выполняются следующие неравенства:

А (s) £А ( ), В (s) £В ( ), С (s) £ С ( ),

причем хотя бы одно из них выполняется как строгое неравенство.

Способ конструирования вариантов после-
довательностей s и вычисления оценок D(s) для каждого из них состоит в следующем.

Пусть имеется начальная подпоследовательность s. Тогда вычисляются величины:

d_C (s) = С(s) +, (1)

d_B (s) = В (s) ++ minc_j , (2)

d_A (s) = A (s) + + (3)

где J (s) — множество символов, образующих последовательность s.

За оценку критерия С (s) для варианта s можно принять величину

D(s) = max {d_A (s), d_B (s), d_C (s)}.(4)

Тогда ход решения задачи трех станков можно представить следующей формальной схемой.

Нулевой шаг. Задание множества G⁽⁰⁾ , образуется всеми возможными последовательностями (s = 0).

Вычисление оценки для множества G₀ :

гдеD(0) = max {d_A (0), d_B (0), б_C (0)},

; ; .

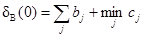Первый шаг.Образование множеств G₁ ⁽¹⁾ UG₁ ⁽²⁾ U... …G₁ ⁽ⁿ⁾ .

Подмножество G_k определяется всеми последовательностями с началом i_k ( k — 1, ...,n ).

Вычисление оценок . Оценку для последовательности s_k определяют из соотношения (4), т. е.

D(s_k ) = max {d_A (s_k ), d_B (s_k ), d_C (s_k )}; k = 1, n.

Выбор варианта для продолжения. Из всех подпоследовательностей, построенных на предыдущем шаге, выбирают наиболее перспективную последовательность s_k с наименьшей оценкой, т. е.

D(s_k ⁽¹⁾ )=min D(s_j ⁽¹⁾ ).

Ветвление. Выбрав наиболее перспективный вариант последовательности s_k ⁽¹⁾ , развивают его построением всех возможных подпоследовательностей длиной 2с началом s_k ⁽¹⁾ вида s_k+1 ⁽²⁾ = (s_k ⁽¹⁾ , j ), где j не входит в s_k .

Вычисление оценок производят в соответствии с соотношениями (1), (2), (3).

k - ш а г. Допустим, что уже проведено k шагов, в результате чего построены варианты s₁ ^(k) ,s₂ ^{( k)} ,…,s_vk ^{( k)} , а именно подпоследовательности длиной k .

Выбираем самый перспективный вариант s_S ^{( k)} такой, что

D(s_s ^(k) )=min D(s_j ^(k) ).

Множество G_s ^{( k )} разбиваем на (п — k ) подмножеств, каждое из которых образуется добавлением к последовательности s_s ^{( k )} некоторого элемента i _{k +1} такого, что i _{k +1} .

Оценка определяется в соответствии с соотношениями (1) — (4).

В результате строим дерево вариантов следующего вида: вершина О отвечает s = 0, вершины первого уровня G ₁ ⁽¹⁾ , G ₂ ⁽¹⁾ ..., G _n ⁽¹⁾ соответствуют последовательностям длиной 1, т. е. s₁ ⁽¹⁾ = 1, s₂ ⁽¹⁾ = 2,..., s_n ⁽¹⁾ = п и т. д. Каждая конечная вершина отвечает последовательности максимальной длины п.

Признак оптимальности. Если s_v ^{( n)} отвечает конечной вершине дерева, причем оценка наименьшая из оценок всех вершин, то s_v ^{( n)} — искомый вариант, иначе переходим к продолжению варианта с наименьшей оценкой.

Пример 6. Рассмотрим задачу .трех станков, условия которой приведены в табл. 1:

Таблица 1

Нулевой шаг. s = 0.

d_A (s = 0) = A(0) + + = 0 + 14 + 3 = 17;

d_B (s = 0) = В(0) + + minc_j = 0 + 15 + 2 = 17;

d_C (s = 0) = С(0) + =14 .

Тогда

∆ (s = 0) = max {17, 17,14} = 17.

Первый шаг. Конструируем все возможные последовательности длиной 1

s₁ ⁽¹⁾ = 1; s₂ ⁽¹⁾ = 2; s₃ ⁽¹⁾ = 3 ; s₄ ⁽¹⁾ = 4 ; s₅ ⁽¹⁾ = 5.

Находим

d_A ⁽¹⁾ = A₁ + + = 14 + 3 = 17;

d_B ⁽¹⁾ (s = 0) = В₁ + + = 5 + 12 + 2 = 19;

d_C ⁽¹⁾ = С₁ + = 9 + 10 = 19 .

Откуда ∆ (1) = max {17, 19, 19} = 19.

Аналогично определяем ∆ (2), ∆ (3), ∆ (4), ∆ (5).

Второй шаг. Среди множества подпоследовательностей длиной 1, s₁ ⁽¹⁾ = 1, s₂ ⁽¹⁾ = 2,..., s₅ ⁽¹⁾ = 5 выбираем наиболее перспективную s = 1, для которой величина оценки-прогноза ∆ (s) оказывается наименьшей. Далее развиваем ее, конструируя возможные варианты длиной 2, т. е. (1.2), (1.3), (1.4), (1.5).

Для каждого из этих вариантов вновь определяем оценки по формулам (1) — (4).

Процесс вычислений продолжаем аналогично.

Процесс построения дерева вариантов приведен на рис. 1.

Каждой конечной вершине дерева вариантов будет отвечать полная последовательность s = i ₁ ,i _2, ,.i_n . Если для некоторой такой вершины величина оценки ∆ (s) не превосходит величины оценок для всех остальных вершин, то эта оценка определяет искомый оптимальный вариант. В противном случае разбиваем более перспективный вариант с наилучшей оценкой.

Конечная вершина определяет вариант (последовательность) = 3, 1, 5, 2, 4 с наилучшей оценкой ∆ = 20. Поэтому данный вариант является оптимальным.

Непосредственной проверкой убеждаемся, что время обработки всей последовательности деталей для этого варианта совпадает со значением оценки-прогноза и является минимальным:

Летература

1)Зайченко Ю. П., «Исследование операций», Киев «Высшая школа» 1975г.

2)Акулич И.Л., «Математическое программирование в примерах и задачах», Москва «В ысшая школа» 1993г.

3)Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. «Математическое программирование», Москва «В ысшая школа» 1980г.