ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Авиа- и ракетостроение»
Специальность 160801- «Ракетостроение»
Курсовая работа
по дисциплине «Теория автоматического регулирования»
АНАЛИЗ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ УГЛОВОЙ СКОРОСТИ ВРАЩЕНИЯ ТУРБИНЫ
Выполнил: студент
гр.
Руководитель:
Омск 2007
Задание
1. Написать уравнения, передаточный функции элементов. Составить структурную схему. Определить передаточные функции разомкнутой, замкнутой систем и передаточную функцию по ошибке.
2. Построить частотные характеристики (АЧХ, ФЧХ) системы, ЛАЧХ разомкнутой системы, переходную характеристику.
3. Исследовать систему на устойчивость. Определить запасы устойчивости.
4. Определить коэффициенты ошибок. Найти установившуюся ошибку Dx(t) при функции входного сигнала xВХ
(t) = 1; t; t2
.
5. Определить показатели качества (время регулирования, перерегулирование, колебательность переходного процесса).
6. Определить параметры корректирующего звена, обеспечивающие наибольшее быстродействие при достаточном запасе устойчивости (по амплитуде не менее 6 дБ, по фазе не менее 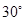 ). ).
Исходные данные
| Звено |
Параметр |
Значение |
| Гидротурбина |
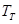 , с , с |
5 |
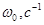 |
1 |
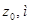 |
0,2 |
| Гидропривод |
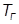 , с , с |
0,001 |
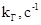 |
1000 |
| Центробежный тахометр |
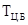 , с , с |
0,1 |
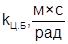 |
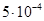 |
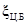 |
0,1 |
| Изодром |
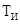 , с , с |
0,03 |
| Редуктор |
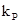 |
1 |
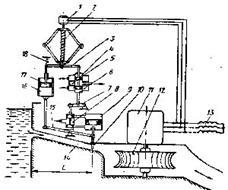
Рис.1. Система автоматического регулирования угловой скорости вращения гидротурбины
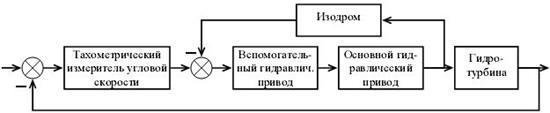
Рис.2. Блок-схема системы автоматического регулирования угловой скорости вращения гидротурбины
Выполнение работы
1. Передаточные функции элементов системы (звеньев)
Это выполняется в два действия:
- Из исходного дифференциального уравнения элемента САУ получить уравнение в операторной форме. Это выполняется путем замены производной 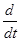 оператором дифференцирования p. оператором дифференцирования p.
- Из полученного алгебраического уравнения выразить отношение выходной величины к входной. Это отношение равно передаточной функции.
Центробежный тахометр
Уравнение элемента: 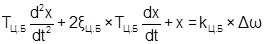 . .
Уравнение в операторной форме:
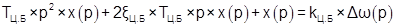 . .
Входным сигналом является угловая частота вращения 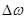 , выходным – перемещение нижней муфты , выходным – перемещение нижней муфты 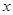 . Получим передаточную функцию: . Получим передаточную функцию:
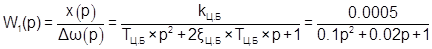 . .
Вспомогательный гидропривод
Так как по условию перемещение гидроусилителя 6 равно перемещению золотника 4, т.е. значения входного и выходного сигналов равны, то 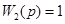 . .
Основной гидропривод
Уравнение элемента: 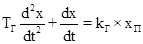 . .
Уравнение в операторной форме:
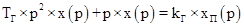 . .
Входным сигналом является перемещение штока золотника 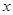 , выходным – перемещение штока поршня , выходным – перемещение штока поршня  . Получим передаточную функцию: . Получим передаточную функцию:
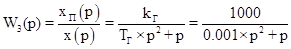 . .
Изодром
Уравнение элемента:
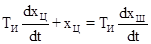 . .
Уравнение в операторной форме:
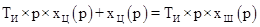 . .
Входным сигналом является перемещение цилиндра изодрома 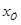 , выходным – перемещение штока поршня , выходным – перемещение штока поршня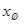 . Получим передаточную функцию: . Получим передаточную функцию:
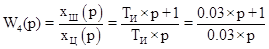 . .
Гидротурбина
Уравнение элемента:
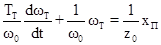 . .
Уравнение в операторной форме:
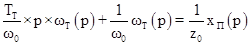 . .
Входным сигналом является перемещение задвижки  , выходным –угловая скорость вращения вала гидротурбины , выходным –угловая скорость вращения вала гидротурбины 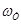 . Получим передаточную функцию: . Получим передаточную функцию:
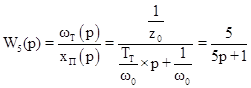 . .
Усилитель
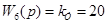 - коэффициент усиления (скорость двигателя 1 в 20 раз выше скорости гидротурбины 12). - коэффициент усиления (скорость двигателя 1 в 20 раз выше скорости гидротурбины 12).
Редуктор
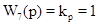 . .
Структурная схема системы регулирования будет выглядеть следующим образом:
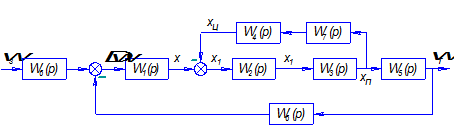
Рис. 1. Структурная схема системы автоматического регулирования угловой скорости вращения гидротурбины
Изобразим структурную схему с учётом исходных данных:
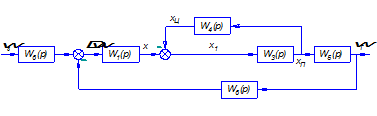
Рис. 2. Структурная схема САУ
Проведём преобразования структурной схемы.
Объединим звено с передаточной функцией 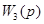 со звеном отрицательной обратной связи со звеном отрицательной обратной связи 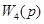 : :
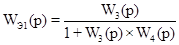 . .
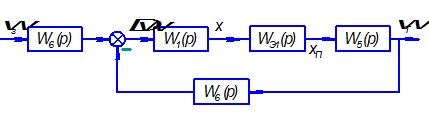
Перенесём сумматор с правой стороны усилителя (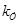 ) в левую, добавив в цепь обратной связи звено ) в левую, добавив в цепь обратной связи звено 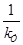 . .
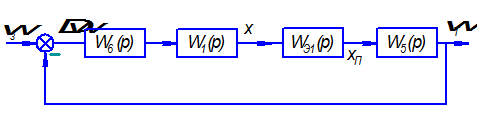
Объединим последовательные звенья:
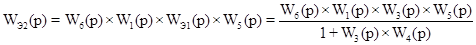
Передаточная функция эквивалентного звена 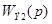 является передаточной функцией разомкнутой системы: является передаточной функцией разомкнутой системы:
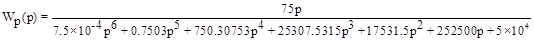
Передаточная функция замкнутой системы:
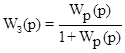
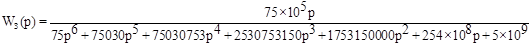 . .
В общем виде
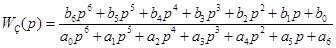 , (74) , (74)
где 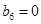 , , 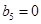 , , 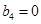 , , 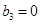 , , 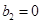 , , 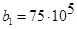 , , 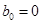 ; ;  , , 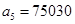 , , 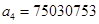 , , 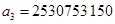 , , 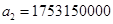 , , 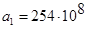 , , 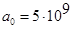 . .
Передаточная функция по ошибке:
 . .
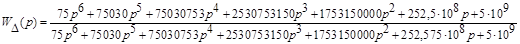
Модель данной системы, составленная в MATLAB / SIMULINK, имеет следующий вид:

Рис. 3. Модель замкнутой САУ, составленная в MATLAB / SIMULINK
Для проверки корректности модели следует подать на вход системы какой-либо сигнал и посмотреть поведение выходного сигнала. В качестве входного используем ступенчатый сигнал (блок Step), выходной сигнал выведем на график с помощью осциллографа Scope.

Рис. 4. Результат работы модели САУ в MATLAB / SIMULINK
2. Построение частотных характеристик (АЧХ, ФЧХ) системы, ЛАЧХ разомкнутой системы, переходной характеристики
На рис.3 показана модель замкнутой системы. Чтобы построить характеристику для разомкнутой системы (кривую Найквиста), необходимо разорвать главную обратную связь (рис.5).
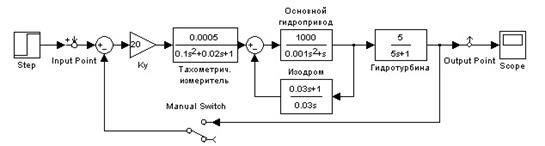
Рис. 5. Модель разомкнутой САУ, составленная в MATLAB / SIMULINK
Имея модель САУ в SIMULINK, легко построить её частотные и переходную характеристики с помощью другого инструмента: LTIViewer. Он предназначен для анализа линейных стационарных систем. С помощью данного инструмента можно построить частотные характеристики исследуемой системы, получить её отклики на единичные ступенчатое и импульсное воздействия, построить годограф Найквиста и т.д.
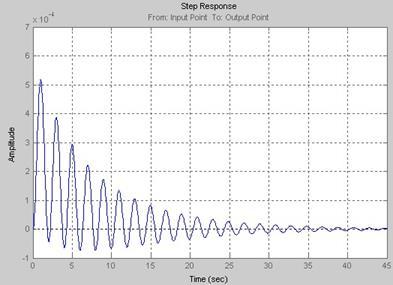
Рис. 5. Переходный процесс САУ
Для построения амплитудно-частотной характеристики (АЧХ) замкнутой системы производят подстановку 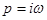 в выражение для передаточной функции замкнутой системы в выражение для передаточной функции замкнутой системы 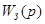 и АЧХ строят по выражению: и АЧХ строят по выражению: 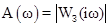 . .
Фазо-частотная характеристика (ФЧХ) замкнутой системы строится по выражению:
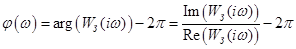 , ,
т. е. как аргумент комплексной передаточной функции замкнутой системы.  , , 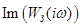 - соответственно действительная и мнимая части комплексной передаточной функции замкнутой системы - соответственно действительная и мнимая части комплексной передаточной функции замкнутой системы 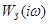 . .
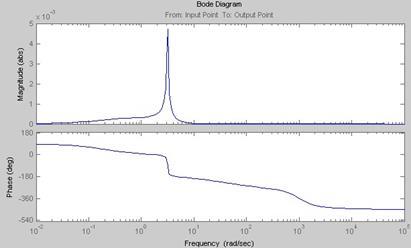
Рис. 6. АЧХ и ФЧХ замкнутой системы
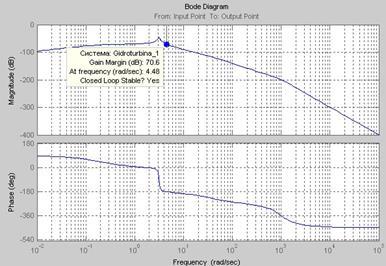
Рис. 7. Логарифмические частотные характеристики разомкнутой САУ
3. Исследование системы на устойчивость
Критерий Гурвица
Характеристическое уравнение замкнутой системы в общем виде имеет вид:
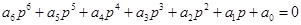 (91) (91)
Составим определители Гурвица:
 , , 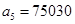 , , 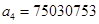 , , 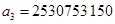 , , 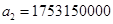 , , 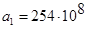 , , 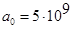 . .
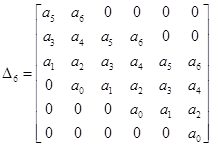 ; ; 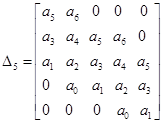 ; ; 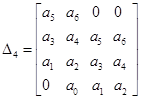 ; ;
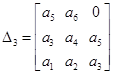 ; ; 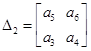 ; ; 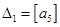 . .
Программа анализа устойчивости САУ:
% Анализ устойчивости САУ по Гурвицу
% Коэффициенты характеристического уравнения замкнутой системы:
a7=75;
a6=75030;
a5=75030753;
a4=2530753150;
a3=1753150000;
a2=254*1.0e+8;
a1=5*1.0e+9;
% a - вектор коэффициентов характеристического уравнения замкнутой системы
% a(7)*p^6+a(6)*p^5+a(5)*p^4+a(4)*p^3+a(3)*p^2+a(2)*p^1+a(1)
% нумерация начинается с единицы, а не с нуля
a = [a1 a2 a3 a4 a5 a6 a7];
disp('ВычислениеопределителейГурвица:');
A6=[a(6) a(7) 0 0 0 0; a(4) a(5) a(6) a(7) 0 0; a(2) a(3) a(4) a(5) a(6) a(7);
0 a(1) a(2) a(3) a(4) a(5); 0 0 0 a(1) a(2) a(3); 0 0 0 0 0 a(1)]
d6=det(A6)
A5=[a(6) a(7) 0 0 0; a(4) a(5) a(6) a(7) 0; a(2) a(3) a(4) a(5) a(6);
0 a(1) a(2) a(3) a(4); 0 0 0 a(1) a(2)]
d5=det(A5)
A4=[a(6) a(7) 0 0; a(4) a(5) a(6) a(7); a(2) a(3) a(4) a(5); 0 a(1) a(2) a(3)]
d4=det(A4)
A3=[a(6) a(7) 0; a(4) a(5) a(6); a(2) a(3) a(4)]
d3=det(A3)
A2=[a(6) a(7); a(4) a(5)]
d2=det(A2)
A1=[a(6)]
d1=det(A1)
ifd6>0 && d5>0 && d4>0 && d3>0 && d2>0 && d1>0
s='Так как все определители Гурвица больше нуля, то система УСТОЙЧИВА';
else
s='Так как не все определители Гурвица положительны, то система НЕ УСТОЙЧИВА';
end
disp(s);
Результат работы программы:
>> Вычисление определителей Гурвица:
A6 = 1.0e+010 *
0.0000 0.0000 0 0 0 0
0.2531 0.0075 0.0000 0.0000 0 0
2.5400 0.1753 0.2531 0.0075 0.0000 0.0000
0 0.5000 2.5400 0.1753 0.2531 0.0075
0 0 0 0.5000 2.5400 0.1753
0 0 0 0 0 0.5000
d6 = 8.7654e+050
A5 = 1.0e+010 *
0.0000 0.0000 0 0 0
0.2531 0.0075 0.0000 0.0000 0
2.5400 0.1753 0.2531 0.0075 0.0000
0 0.5000 2.5400 0.1753 0.2531
0 0 0 0.5000 2.5400
d5 = 1.7531e+041
A4 = 1.0e+010 *
0.0000 0.0000 0 0
0.2531 0.0075 0.0000 0.0000
2.5400 0.1753 0.2531 0.0075
0 0.5000 2.5400 0.1753
d4 = 1.3753e+031
A3 = 1.0e+010 *
0.0000 0.0000 0
0.2531 0.0075 0.0000
2.5400 0.1753 0.2531
d3 = 1.3757e+022
A2 = 1.0e+009 *
0.0001 0.0000
2.5308 0.0750
d2 = 5.4398e+012
A1 = 75030
d1 = 75030
Так как все определители Гурвица больше нуля, то система УСТОЙЧИВА.
Критерий Михайлова
Построим годограф Михайлова – кривую, которая описывается характеристическим вектором на комплексной плоскости. Характеристический вектор получим, подставив 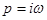 в характеристический полином (знаменатель передаточной функции замкнутой системы): в характеристический полином (знаменатель передаточной функции замкнутой системы):
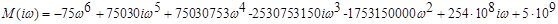
Программа анализа устойчивости САУ:
disp (' *** Анализ устойчивости по критерию Михайлова ***');
% знаменатель характеристического уравнения замкнутой системы
% a(7)*p^6+a(6)*p^5+a(5)*p^4+a(4)*p^3+a(3)*p^2+a(2)*p^1+a(1), гдевектор a найденранее
for i=1:1101
w(i)=i-1;% вектор значений частот
end
N=length(w);
for k=1:N
M(k)=-a(7)*w(k)^6+a(6)*j*w(k)^5+a(5)*w(k)^4-a(4)*j*w(k)^3-a(3)*w(k)^2+a(2)*j*w(k)+a(1);
end
x=real(M); % действительная часть
y=imag(M); % мнимаячасть
plot(x,y); grid on;
В результате получаем график (рис. 8,а,б).
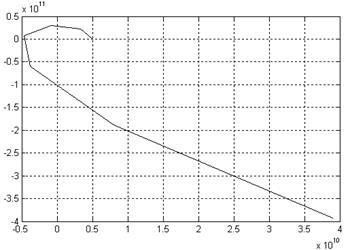
а)
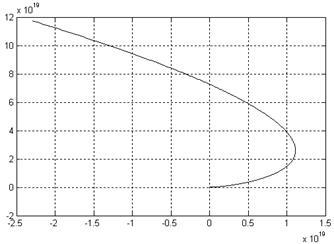
б)
Рис.8. Кривая Михайлова: а) 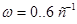 , б) , б) 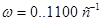
Характеристический полином имеет степень 6-го порядка, следовательно, для устойчивости данной системы необходимо, чтобы характеристический вектор описывал угол 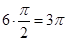 , т.е. последовательно проходил шесть квадрантов комплексной плоскости. Так как это условие выполняется, то система является устойчивой. , т.е. последовательно проходил шесть квадрантов комплексной плоскости. Так как это условие выполняется, то система является устойчивой.
Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики (АФЧХ) разомкнутой системы.
АФЧХ разомкнутой системы, строим в программе MATLAB/SIMULINK с помощью инструмента LTIViewer.
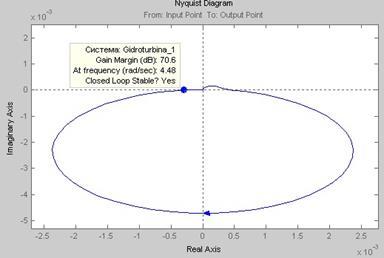
Рис.9. АФЧХ (кривая Найквиста) разомкнутой системы
Так как кривая Найквиста не охватывает точку (-1;i0), то система является устойчивой.
Запасы устойчивости
Запасы устойчивости определим графически по ЛЧХ разомкнутой системы (рис.7).
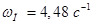
Запас устойчивости по амплитуде  . .
По определению частота среза 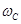 - это частота, при которой АФЧХ пересекает окружность единичного радиуса с центром в точке (0;i0). Но, так как кривая Найквиста расположена внутри единичной окружности (рис.9) и не пересекает её, то частота среза отсутствует. Откуда следует, что фаза может изменяться в любых пределах без риска для устойчивости системы. - это частота, при которой АФЧХ пересекает окружность единичного радиуса с центром в точке (0;i0). Но, так как кривая Найквиста расположена внутри единичной окружности (рис.9) и не пересекает её, то частота среза отсутствует. Откуда следует, что фаза может изменяться в любых пределах без риска для устойчивости системы.
Вывод: система устойчива.
4. Оценка точности САУ
Если передаточную функцию по ошибке
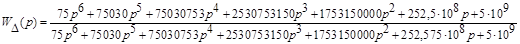
представить в виде степенного ряда
 , ,
то коэффициенты 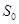 , ,  , , 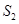 , … называют коэффициентами ошибок. Их можно определить по известным формулам , … называют коэффициентами ошибок. Их можно определить по известным формулам
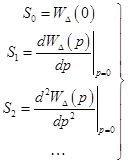
Затем величину ошибки можно рассчитать по формуле
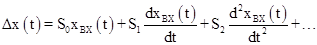
В задании требуется определить ошибку при xВХ
(t) = 1; t; t2
.
Программа расчёта величины ошибки:
disp (' *** Определение коэффициентов ошибок ***');
syms p Wd x dx t % p, Wd, x, dx - символьные переменные
a(2)=252.5*1.0e+8;
disp (' Передаточная функция по ошибке ');
Wd=(a(7)*p^6+a(6)*p^5+a(5)*p^4+a(4)*p^3+a(3)*p^2+a(2)*p+a(1))/(a(7)*p^6+a(6)*p^5+a(5)*p^4+
+a(4)*p^3+a(3)*p^2+(a(2)+0.075*1.0e+8)*p+a(1));
pretty(Wd) % выводвудобочитаемомвиде
disp (' Коэффициенты ошибок ');
S0=subs(diff(Wd,p,0),p,0)
S1=subs(diff(Wd,p,1),p,0)
S2=subs(diff(Wd,p,2),p,0)
S3=subs(diff(Wd,p,3),p,0)
S4=subs(diff(Wd,p,4),p,0)
S5=subs(diff(Wd,p,5),p,0)
S6=subs(diff(Wd,p,6),p,0)
disp (' ');
disp ('Определение ошибки при различных функциях входного сигнала');
x=1
dx=eval(S0*x+S1*diff(x,t)+S2*diff(x,t,2)+S3*diff(x,t,3)+S4*diff(x,t,4)+S5*diff(x,t,5)+S6*diff(x,t,6))
%pretty(dx)
x=t
dx=eval(S0*x+S1*diff(x,t)+S2*diff(x,t,2)+S3*diff(x,t,3)+S4*diff(x,t,4)+S5*diff(x,t,5)+S6*diff(x,t,6));
pretty(dx)
x=t^2
dx=eval(S0*x+S1*diff(x,t)+S2*diff(x,t,2)+S3*diff(x,t,3)+S4*diff(x,t,4)+S5*diff(x,t,5)+S6*diff(x,t,6));
pretty(dx)
Результат работы программы:
*** Определение коэффициентов ошибок ***
Передаточная функция по ошибке
6 5 4 3 2
(75 p + 75030 p + 75030753 p + 2530753150 p + 1753150000 p
/ 6 5 4
+ 25250000000 p + 5000000000) / (75 p + 75030 p + 75030753 p
/
3 2
+ 2530753150 p + 1753150000 p + 25257500000 p + 5000000000)
Коэффициентыошибок
S0 = 1
S1 = -0.0015
S2 = 0.0152
S3 = -0.2265
S4 = 4.5312
S5 = -113.3155
S6 = 3.4005e+003
Определение ошибки при различных функциях входного сигнала
x = 1
dx = 1
x = t
211106232533
t - ----------------------
140737488355328
x = t^2
2 211106232533 34124900276475
t - --------------------- t + ------------------------
70368744177664 1125899906842624
При  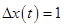 (система статическая). (система статическая).
При  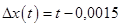 (скоростная ошибка линейно возрастает с течением времени). (скоростная ошибка линейно возрастает с течением времени).
При  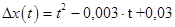 (ошибка от ускорения с течением времени изменяется по квадратичному закону). (ошибка от ускорения с течением времени изменяется по квадратичному закону).
5. Показатели качества переходного процесса
Для определения показателей качества переходного процесса проанализируем переходную характеристику на рис.10.
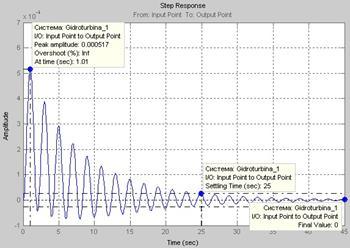
Рис.10. Переходная характеристика САУ
Будем определять следующие показатели качества переходного процесса: время регулирования переходного процесса 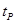 , недорегулирование , недорегулирование  , колебательность переходного процесса , колебательность переходного процесса 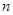 . .
Время регулирования переходного процесса 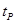 характеризует быстродействие системы и определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины характеризует быстродействие системы и определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины 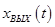 от её установившегося значения от её установившегося значения 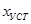 становится меньше определённой достаточно малой величины (5% становится меньше определённой достаточно малой величины (5%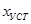 ). ).
Время регулирования переходного процесса 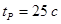 . .
Колебательность переходного процесса 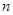 обычно определяется числом колебаний равным числу максимумов (минимумов) переходной характеристики за время регулирования обычно определяется числом колебаний равным числу максимумов (минимумов) переходной характеристики за время регулирования 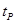 . .
Колебательность переходного процесса 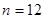 . .
Недорегулирование  характеризует перегрузку в системе, это максимальное отклонение переходной характеристики относительно характеризует перегрузку в системе, это максимальное отклонение переходной характеристики относительно 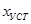 , выраженное в %-ах от него. Для большинства систем , выраженное в %-ах от него. Для большинства систем 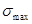 обычно не превышает 30%. Недорегулирование вычисляется по формуле: обычно не превышает 30%. Недорегулирование вычисляется по формуле:
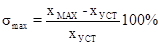 , ,
где 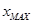 - максимальное значение, достигаемое переходной характеристикой. - максимальное значение, достигаемое переходной характеристикой.
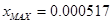 . .
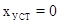 . .
6. Коррекция динамических свойств системы
Простейшим способом повышения качества САУ является подбор значений параметров её элементов.
Новые значения параметров звеньев:
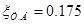 ; ; 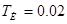 . .
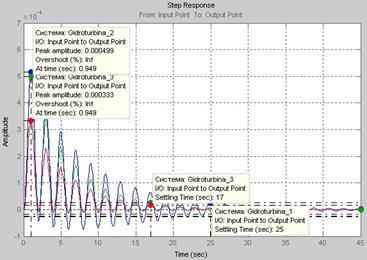
Рис.11. Графики переходной характеристики САУ до и после корректирования
Время регулирования переходного процесса 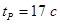 . .
Колебательность переходного процесса 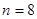 . .
Максимальное значение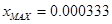 . .
Запас устойчивости системы увеличился (рис.12).
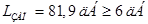 . .
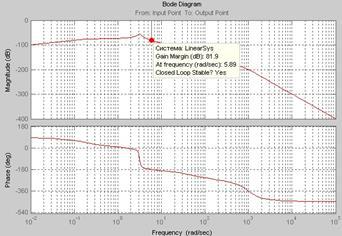
Рис.12. ЛЧХ разомкнутой САУ
Список литературы
1. Черных И.В. "Simulink: Инструмент моделирования динамических систем" (simulink.chm)
2. Теория автоматического управления. Методические указания для самостоятельной работы студентов. Ситников Д.В. Омск: ОмГТУ, 2003.
|