| зміст
Вступ
1. Основи статистики фононів
1.1 Фонони
1.2 Наближення Ейнштейна и Дебая
2. Нормальні процеси і процеси перебросу
3. Вплив N-процесів
4. Облік нормальних процесів
4.1 Релаксаційний метод
4.2 Варіаційний метод
4.3 Метод Гюйє і Крумхансла
Висновки
Список використаної літератури
вступ
Однією з характерних особливостей розвитку сучасного суспільства є широке використання у всіх його сферах досягнень науки і техніки. Важливий вклад у науково-технічний прогрес вносить фізика, зокрема фізика твердого тіла.
Фізика твердого тіла — це великий і важливий розділ сучасної фізики, який вивчає структуру і фізичні властивості речовин у твердому стані. Основне завдання фізики твердого тіла зводиться до встановлення зв'язку між властивостями індивідуальних атомів чи молекул і тими властивостями, які проявляються при об'єднанні цих атомів або молекул в кристали. Важко собі уявити розвиток таких напрямків науки і техніки, як фізика напівпровідників, металів, надпровідників, металургія, матеріалознавство, електроніка, мікро- та оптоелектроніка тощо без фізики твердого тіла.
Постійно створюються і впроваджуються в практику принципово нові матеріали і прогресивні технології. Це, насамперед, надчисті металеві, надпровідні, напівпровідникові матеріали, різні полімерні матеріали і вироби з них, жароміцні та хімічно стійкі замінники металів, порошкові матеріали, тугоплавкі сполуки тощо. Зростаючі потреби сучасної техніки в нових матеріалах істотно стимулюють розвиток фізики твердого тіла як науки матеріалознавчої. Досить нагадати, що завдяки розвитку фізики і хімії твердого тіла ми маємо тепер такі важливі нові матеріали, як рідкі кристали, високотемпературні надпровідники, органічні напівпровідники, провідники і надпровідники тощо.
Тому не дивно, що майже половина всіх фізиків планети працюють у різних областях фізики твердого тіла.
Якщо раніше тверді тіла застосовувалися в техніці майже виключно як конструкційний матеріал, то в міру накопичення знань про фізику твердого тіла, технічні застосування останнього стають набагато обширнішими і різноманітнішими. Зараз тверді тіла грають самостійну роль, виконуючи функції тонких фізичних приладів (оптичних, напівпровідникових, надпровідних і т. д.).
Впорядкованість будови кристалічних твердих тіл і пов'язана з цим анізотропія їх властивостей зумовили широке застосування кристалів в науці і техніці.
Кристали дозволили з'ясувати фізичну природу рентгенівських променів, вивчити хвилеві властивості електронів, дали можливість провести широкий комплекс досліджень в поляризованому світлі, допомогли розгадати багато інших загадок науки.
Вивчення властивостей твердого тіла відкриває можливості створення нових матеріалів, яких не створила природа. Сюди відносяться жароміцні або, навпаки, дуже легкоплавкі сплави, надтверді матеріали, речовини, що володіють цікавими електричними властивостями (напівпровідники), магнітними властивостями (феромагнетики і ферити), речовини, що володіють високою хімічною стійкістю, нові універсальні стеклокристалічні матеріали — ситалли, металокерамічні матеріали — кермети, що поєднують як властивості вогнетривких оксидів, так і властивості металів, полімери з наперед заданими властивостями і т.д.
1. основи статистики фононів
1.1 Фонони
Коливання N
атомів кристала можна виразити через суперпозицію 3N
нормальних коливань, або мод. Оскільки кожне нормальне коливання з механічної точки зору можна подати як гармонічний осцилятор, то повна енергія коливань дорівнює сумі енергій коливань 3N
гармонічних осциляторів, що не взаємодіють між собою. Згідно з квантовою механікою, енергія осцилятора, що коливається з частотою ω
j
( ), ),

(1.1)
а повну енергію коливань кристала можна записати у вигляді суми
 (1.2) (1.2)
де n — 0, 1, 2, 3, ...,
— 0, 1, 2, 3, ...,  — хвильовий вектор, який може: набувати N
різних значень; j
— індекс вітки коливань. — хвильовий вектор, який може: набувати N
різних значень; j
— індекс вітки коливань.
Одним з основних результатів квантового підходу дослідження властивостей кристалів є концепція квазічастинок. Квазічастинки перебувають в тому об'ємі, в якому знаходиться система реальних частинок, бути поза системою вони не можуть. Рух кожної окремої квазічастинки ідентичний руху великої кількості реальних частинок системи. Як і справжні частинки, квазічастинки бувають ферміонами і бозонами.
Із (1.2) видно, що енергія збудженого кристала біля основного стану є сумою енергії основного стану і енергії газу квазічастинок. Відповідно енергія збудженого стану системи нормальних коливань кристалічної решітки дорівнює різниці її повної енергії, що виражається сумою (1.2), і енергії основного (незбудженого) стану — енергії нульових коливань

:

З електронами провідності взаємодіють тільки ці збудження, а нульові коливання утворюють постійний незмінний фон (вакуум) кристала. Проте, коли амплітуди нульових коливань атомів стають порівнянними із сталою решітки, то такі квантові кристали набувають деяких дуже цікавих властивостей; такі властивості при певних умовах мають кристали твердого гелію.
Вираз (1.3) можна розглядати, як суму енергій ħω
j
( ) певних квазічастинок, кількість яких дорівнює n ) певних квазічастинок, кількість яких дорівнює n . Енергія ħω
j
(
. Енергія ħω
j
( ) називається квантом енергії коливання решітки або фононом. Отже, фонон — це одиничне квантове збудження нормального коливання. За аналогією з фотоном (квантом електромагнітного поля) фонон можна розглядати як вільну квазічастинку. У цьому разі ∆ n ) називається квантом енергії коливання решітки або фононом. Отже, фонон — це одиничне квантове збудження нормального коливання. За аналогією з фотоном (квантом електромагнітного поля) фонон можна розглядати як вільну квазічастинку. У цьому разі ∆ n = +1 означає народження фонона, а n
= +1 означає народження фонона, а n = –1 — його знищення.
= –1 — його знищення.
Таким чином, поки теплова енергія кристала досить мала і коливання атомів гармонічні, її можна подати у вигляді суми енергій квазічастинок — фононів
, що не взаємодіють. В гармонічному наближенні фонони за багатьма своїми властивостями поводять себе, як ідеальний газ.
Фонони є акустичні
і оптичні
, а якщо врахувати поляризацію,— поздовжні
(L
) і поперечні
(Т
), тобто фонони бувають LA
, LO
, ТА
і ТО
. Оскільки фонон характеризується хвильовим вектором  , то для нього властивий і відповідний закон дисперсії коливань ω
( , то для нього властивий і відповідний закон дисперсії коливань ω
( ), причому в тривимірному випадку (як і в одновимірному) закон дисперсії є періодичною функцією з періодом решітки. Це означає, що існує певний зв'язок між типом кристала, його симетрією і характером коливань атомів (або симетрією фононів). У вивченні фононного спектра найбільш важливим є вид дисперсії фононів в особливих точках ), причому в тривимірному випадку (як і в одновимірному) закон дисперсії є періодичною функцією з періодом решітки. Це означає, що існує певний зв'язок між типом кристала, його симетрією і характером коливань атомів (або симетрією фононів). У вивченні фононного спектра найбільш важливим є вид дисперсії фононів в особливих точках  -простору, тобто у високосиметричних точках, наприклад в точках |q| = 0, | -простору, тобто у високосиметричних точках, наприклад в точках |q| = 0, | | = | =  тощо. тощо.
Згідно з квантовою статистикою Бозе — Ейнштейна, середнє число фононів, які мають енергію Еф
= ħω
, задається функцією

(1.4)
Формула (1.4) враховує, що хімічний потенціал рівноважного фононного газу дорівнює нулю, оскільки загальна кількість фононів у кристалі не зберігається.
Відповідно середню енергію фононів, які перебувають у стані з відомими ω
і  , записують як , записують як

(1.5)
1.2 Наближення Ейнштейна і Дебая
В основу першої квантової теорії твердих тіл покладено модель Ейнштейна (1907 p.). Згідно з нею атом кристала являє собою тривимірний гармонічний осцилятор, що виконує коливання з частотою ωЕ
поблизу положення рівноваги незалежно від інших атомів. Згідно з цією моделлю, тверде тіло слід розглядати як сукупність 3N
квантових осциляторів, що мають однакову частоту. Середня енергія кожного осцилятора визначається за формулою (1.5).
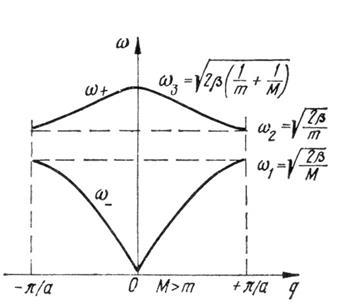
З рис. 1.1 видно, що частоти оптичних коливань кристалічної решітки мало залежать від хвильового вектора  . Це означає, що до них можна застосувати модель Ейнштейна. За частоту коливань ωЕ
осциляторів беруть ω
3
, яка дорівнює граничному значенню частоти оптичної вітки коливань (рис. 1.1). В моделі твердого тіла Ейнштейна енергію кристала, який містить N
атомів, записують так: . Це означає, що до них можна застосувати модель Ейнштейна. За частоту коливань ωЕ
осциляторів беруть ω
3
, яка дорівнює граничному значенню частоти оптичної вітки коливань (рис. 1.1). В моделі твердого тіла Ейнштейна енергію кристала, який містить N
атомів, записують так:
 (1.6) (1.6)
У виразі (1.6) введено температуру Ейнштейна

(1.7)
 що відповідає збудженню фононів частоти ωf
, кількість яких експоненціально зменшується із зниженням температури. що відповідає збудженню фононів частоти ωf
, кількість яких експоненціально зменшується із зниженням температури.
Рис. 1.1
В моделі твердого тіла Ейнштейна вважається, що кожен атом коливається незалежно від інших. Щоб врахувати зв'язок між сусідніми атомами, П. Дебай (1912 р.) розглянув тверде тіло як суцільне пружне середовище. В такій моделі внутрішня енергія твердого тіла пов'язується не з коливаннями окремих атомів, а з стоячими пружними хвилями (модами). Квант коливальної енергії твердого тіла (фонон) переміщується з швидкістю звуку, оскільки власне звукові хвилі пружні. З рис. 1.1 видно, що для всіх значень хвильового числа q
ωак
< ωоп
, Де ωак
— частоти акустичних коливань, що відповідають нижній вітці (раніше позначали ω_), а ωоп
— частоти оптичних коливань раніше позначали (ω+
). Енергетично це означає, що при досить низьких температурах у кристалі збуджені одні тільки акустичні коливання. Через велике число атомів спектр цих коливань можна вважати практично неперервним і таким, що змінюється від ω = 0 до ω1
(рис. 1.1).
Якщо ввести характеристичну температуру (температура Дебая)

(1.8)
то при Т
≤ θd
вкладом оптичних коливань в енергію кристала можна знехтувати.
Для деяких твердих тіл значення θd
наведено в табл. 1.1.
Рівноважне число акустичних фононів з енергією ħ
ω
в комірці фазового простору об'ємом (2πħ
)3
визначають зa формулою (1.4); число комірок фазового простору, що припадає на інтервал,

(1.9)
де V
— об'єм кристала. Під фазовим простором системи розуміють 6N
-вимірний простір узагальнених координат і узагальнених імпульсів системи.
Якщо вважати дисперсію акустичних частот, згідно з (1.8), лінійною функцією q
і замінити три акустичні вітки коливань однією (що еквівалентно припущенню, за яким швидкість поширення трьох акустичних хвиль однакова), то (1.9) можна звести до вигляду
 (1.10) (1.10)
Тут множник 3 відповідає трьом акустичним модам (одній поздовжній і двом поперечним), а v
— середня швидкість поширення звуку.
Таблиця 1.1
Температури плавлення, Дебая, Фермі і теплоємність
деяких твердих тіл
| Кристал
|
Густина 1)
,
103
кг/м3
|
Тпл
|
θD
, К
|
θF
, К
|
Ср
,
Дж/
(моль•К)
|
| Ne
|
1,503 (10 К)
|
25,4
|
63
|
—
|
20,79
|
| Ar
|
1,656 (40 К)
|
83,9
|
85
|
—
|
20,79
|
| C (алмаз)
|
3,516
|
сублімується
|
1860
|
—
|
6,12
|
| Ge
|
5,324
|
1231
|
366
|
—
|
23,4
|
| Na
|
0,966
|
370,9
|
150
|
—
|
28,12
|
| K
|
0,862
|
336,3
|
10
|
—
|
29,51
|
| Cu
|
8,933
|
1356
|
344,4
|
8,12•104
|
24,47
|
| Au
|
19,281
|
1336
|
161,6
|
6,39•104
|
25,38
|
| NaCl
|
2,167
|
1074
|
321,9
|
—
|
50,79
|
| KBr
|
2,75
|
1003
|
152,8
|
—
|
51,51
|
1)
Дані для 293 К
Вираз (1.10) можна спростити, якщо врахувати умову, що загальне число коливань в трьох акустичних вітках дорівнює 3N
, тобто числу ступенів вільності кристала, що містить N
атомів:  = 3N
.
Звідси максимальна частота, що обмежує спектр нормальних акустичних коливань, = 3N
.
Звідси максимальна частота, що обмежує спектр нормальних акустичних коливань,

(1.11)
З урахуванням (1.4), (1.10) і (1.11) загальне число фононів в об'ємі V
кристала і в інтервалі [ω, ω + dω] (що містить N
атомів)

Відповідно повна енергія акустичних фононів в об'ємі

(1.12)
При одержанні (1.12) використано вираз (1.8) для температури Дебая, покладено х = ħω
/k
Т
і введено функцію Дебая

(1.13)
При високих температурах суттєвим стає вплив оптичних коливань на значення фононної енергії кристала.
2. Нормальні процеси і процеси перебросу
Оскільки ħω
– це квант енергії моди з частотою ω,
то вираз
ω1
+ ω2
= ω3
(2.1.а)
представляє собою закон збереження енергії для трифонного процесу. Мода, строго кажучи, не володіє механічним імпульсом як матеріальна частинка, проте величина ħq
багато в чому схожа з імпульсом. Вираз
q1
+ q2
= q3
+ g (2.1.б)
при g = 0 якраз відповідає закону збереження імпульсу. Взаємодія, при якому g = 0, називається нормальним процесом, а взаємодію, при якій g ≠ 0, Пайерлс назвав процесом перебросу. На такі процеси ми посилатимемося як на N- і U-процеси відповідно.
Відмінність між N- і U-процесами можна проілюструвати за допомогою фігур, що зображають плоский поперечний перетин зони Бріллюена.
На рис. 2.1.а
показаний вектор q3
, що представляє суму векторів q1
, і q2
, які проведені з центру зони. На рис. 2.1.б
і 2.1.в
початкові вектори вибрані так, що їх сума, позначена через q'3
виходить за межі зони.
В одновимірному випадку лінійного ланцюжка було показано, що моди із значеннями q
, що відрізняються на величину 2π/а
, відповідають одним і тим же рухам атомів.
Аналогічно в тривимірному випадку атоми рухаються однаково, якщо значення q
у мод відрізняються на вектор оберненої решітки; мода q'3
ідентична моді q3
, що отримується збільшенням або відніманням до q'3
величин 2π/а
(для випадку простої кубічної решітки).
У U-процесах, таким чином, векторні суми в різних частинах виразу (2.1.б
) повинні відрізнятися на вектор g
, якщо всі фонони представлені векторами, які лежать усередині першої зони Бріллюена.
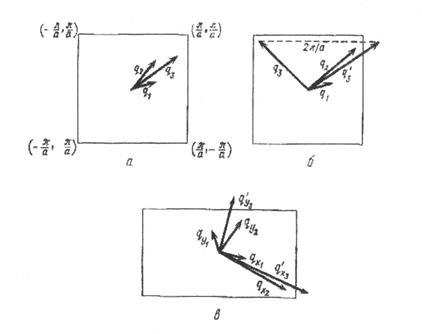
Рис. 2.1. Двовимірне зображення трьох фононних процесів.
а
– результуючий вектор q
, лежить в межах зони Бріллюена – нормальний процес;
б
– результуючий вектор q'3
виходить за межі зони Бріллюена – процес перекидання;
в
– для прямокутної зони Бріллюена мінімальне значення q'3
, при якому відбувається U-процес, залежить від орієнтації вектора q3
.
Теплова енергія переноситься у напрямі групової швидкості фонона. У разі N-процесу напрям потоку енергії в моді q3
. очевидно, співпадає з напрямом, в якому ефективно переноситься енергія модами q1
і q2
. Насправді, якщо взаємодія між фононами здійснюється тільки шляхом N-процесів, то кристал має нескінченну теплопровідність. Після U-процесу теплова енергія передається в напрямі, абсолютно відмінному від напряму групової швидкості в моді q3
. Такі істотні зміни q
завжди приводять до відновлення рівноважного розподілу фононів.
3. Вплив N-процесів
Перш ніж обговорювати слабкий вплив N-процесів на теплопровідність, покажемо, що самі по собі N-процеси не приводять до кінцевої теплопровідності.
Спершу можна пояснити це твердження, провівши аналогію з перебігом газу в трубі. При зіткненнях молекул між собою виконуються закони збереження енергії та імпульсу, і тому ці зіткнення аналогічні N-процесам між фононами. Коли газ при нормальному тиску тече по трубі, його молекули постійно стикаються одна з одною і встановлюється добре відомий розподіл швидкостей, відповідний певній швидкості дрейфу. У реальній ситуації цей розподіл змінюється уздовж поперечного перетину труби, оскільки швидкість дрейфу міняється залежно відстані від осі труби. Якщо стінки труби знаходяться нескінченно далеко, або коли вони абсолютно гладкі, так що при зіткненнях молекули випробовують дзеркальне відображення, або якщо газ міститься в ящику, що проходить по трубі без тертя, то, хоча молекули як і раніше стикаються між собою, опір перебігу газу в трубі відсутній. За цих умов молекули мають певний розподіл швидкостей, який відрізняється від рівноважного розподілу Максвела – Больцмана, відповідного нульовому потоку, але яке не змінюється унаслідок молекулярних зіткнень.
Таким же чином, якщо тепло передається уподовж нескінченно великого ідеального кристала або якщо стінки кристала відображають фонони дзеркально, то N-процеси, що протікають із збереженням енергії та «імпульсу», не змінюють розподілу, який відповідає деякому потоку тепла. Цей розподіл відмінний від рівноважного розподілу Планка. Оскільки є розподіл фононів, що відповідає ненульовому потоку тепла, яке не змінюється внаслідок N-процесів, то N-процеси самі по собі не приводять до появи теплоопору.
Можна більш строго довести неефективність N-процесів за допомогою рис. 2.1.а
, якщо припустити, що всі фонони мають однакові швидкості, паралельні q
. Тоді ω = qυ
і

У N-процесі бере участь по одному фонону з мод q1
і q2
, так що  замінюється на q1
+ q2
. Після процесу замінюється на q1
+ q2
. Після процесу  відповідає q3
. Зміна h
у такому випадку буде рівна відповідає q3
. Зміна h
у такому випадку буде рівна

Потік тепла, отже, не змінюється при N-процесі.
 Такий простий доказ справедливий у відсутність дисперсії, але насправді результат виявляється абсолютно загальним. Один із способів показати це – досліджувати вплив N-процесів на «зміщений» фононний розподіл, що задається формулою Такий простий доказ справедливий у відсутність дисперсії, але насправді результат виявляється абсолютно загальним. Один із способів показати це – досліджувати вплив N-процесів на «зміщений» фононний розподіл, що задається формулою
(3.1)
У формулі (3.1) вектор u
направлений так само, як і потік тепла, і представляє собою швидкість дрейфу. Розподіл відповідає рівноважному, але в системі координат, яка рухається з швидкістю u
. Такий розподіл для одновимірного випадку показаний на рис. 3.1, так що з його асиметричного вигляду ясно, що існує потік тепла в праву сторону.
Вираз для швидкості зміни N
(q
) внаслідок N-процесів, отримане в теорії збурень, містить вірогідність процесу, при якому фонон цієї моди з'являється як кінцевий продукт взаємодії, а також вірогідність процесу, при якому відбувається зникнення фонона цієї моди і в результаті з'являються два інших фонона. Якщо розглянути процес, при якому q1
+ q2
→ q3
, і відповідний зворотний процес, то швидкість зміни N
(q1
) визначається різницею між виразом від прямих процесів

і виразом від зворотних процесів

(такі вагові множники з'являються завжди в системах, що підкоряються статистиці Бозе – Ейнштейна).

Рис. 3.1. Одновимірний асиметричний розподіл фононів,
на який не впливають N-процеси.
Розподіл відповідає потоку тепла вправо. Воно описується формулою (2.1) при u = 0,1 ω/q, Т = 100К. По ординаті відкладено число фононів на одиничний інтервал q.
Якщо підставити формулу (3.1) для N
(q
) в ці два вирази і взяти їх різницю, то просте обчислення приводить до результату:

він визначає швидкість зміни N
(q1
). Якщо умови (2.1) справедливі при g
= 0, тобто мають місце тільки N-процеси, то видно, що швидкість зміни N
(q1
) перетворюється в нуль. Для всіх пар значень q2
і q3
, які можуть брати участь в N-процесах, виходить той же результат, як при процесах q1
→ q2
+ q3
, що впливають на число фононів q1
. Зміщений фононний розподіл, що визначається формулою (3.1) і відповідає ненульовому потоку тепла, таким чином, не змінюється внаслідок N-процесів.
Той же результат можна отримати і за допомогою варіаційного принципу. Для трифононних N-процесів чисельник перетвориться на вигляд:

(3.2)
Якщо записати

(3.3)
де u
'
– довільний вектор, то чисельник міститиме вираз (q1
+ q2
– q3
) • u
'
, яке обертається на нуль, якщо q1
+ q2
= q3
. При такій пробній функції тепловий опір обертається на нуль, що, звичайно, відповідає мінімуму. Таким чином, за допомогою варіаційного принципу знову знаходимо, що у випадку тільки N-процесів теплопровідність нескінченна.
Легко показати, що для малих відхилень від рівноваги вираз для N
(q
), отримуване за допомогою формули (3.3), співпадає з формулою (3.1). З формули (2.1) маємо

 для випадку, коли мало, можна написати для випадку, коли мало, можна написати
 
Підставляючи , знаходимо

Обидва ці вирази співпадають, якщо ħu = u'. Значення u і u' довільні й визначаються величиною потоку тепла; для заданого потоку тепла відхилення від рівноважного розподілу співпадають в обох випадках.
Не слід думати, проте, що оскільки N-процеси самі по собі не приводять до появи теплового опору, то ними можна зовсім нехтувати. Вони можуть істотно впливати на теплопровідність, якщо інтенсивності інших процесів розсіяння залежать від частоти; у такій ситуації N-процеси заважають модам, які розсіюються внаслідок цих процесів, «зноситися» потоком тепла. Багато зусиль було витрачено для того, щоб пояснити, як N-процеси спільно з процесами, які приводять до опору, визначають теплопровідність.
4. ОБЛІК НОРМАЛЬНИХ ПРОЦЕСІВ
4.1 Релаксаційний метод
У простій формі релаксаційного методу передбачається, що кожен механізм розсіяння характеризується часом релаксації, який для даної моди не залежить від населеності фононів у всіх інших модах. Якщо є декілька механізмів розсіяння, то швидкості  , ,  , ... складаються і сумарний час релаксації τ(х
), визначається виразом , ... складаються і сумарний час релаксації τ(х
), визначається виразом

Цей вираз стає, звичайно, складнішим, якщо не користуватися спрощуючими припущеннями теорії Дебая про відсутність дисперсії і квадратичний закон для щільності мод: f
(ω) ~ ω2
.
Оскільки N-процеси самі по собі не приводять до встановлення рівноважного розподілу фононів, то вони не можуть входити в суму для τ(х
) на тих же підставах, що і процеси, що ведуть до встановлення рівноваги (резистивне розсіяння). Проте ними не можна нехтувати, оскільки, перерозподіляючи енергію між модами, вони роблять відчутним для всіх мод наявність резистивних процесів розсіяння, залежних від частоти.
Для аналізу експериментальних даних по теплопровідності широко використовується розгляд Каллуея. Він припустив, що N-процеси переводять будь-який розподіл фононів, що відповідає деякому потоку тепла, в розподіл, визначуваний формулою (3.1), відповідний тому ж потоку тепла і далі вже не змінний внаслідок N-процесів. Час релаксації для таких процесів є τN
(для простоти залежність часу релаксації від q
, поляризації і температури не указується). Повна швидкість зміни N
(q
) дається тоді виразом
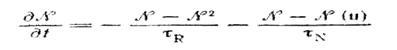
де у величину τR
вносять внесок тільки процеси, що приводять до встановлення рівноважного розподілу N
0
(q
). У моделі Дебая Каллуей, ввівши комбінований час релаксації  , отримав наступний вираз для теплопровідності: , отримав наступний вираз для теплопровідності:

(4.1.1)

де
(4.1.1.а)
 і і
(4.1.1.б)
Цей результат, як видно, знаходиться відповідно до твердження про те, що нормальні процеси впливають на теплопровідність, але трохи інакше, ніж чисто резистивні процеси. У формулу для ϰ1
нормальні процеси входять на тих же підставах, як і інші процеси, оскільки між ними не робиться ніякої відмінності у виразі для τС
. Тому зазвичай вважається, що ϰ1
дає занижену оцінку теплопровідності, проте є другий член ϰ2
, який декілька заповнює її «втрату».
Для пояснення експериментальних результатів часто необхідно користуватися повною формулою (4.1.1); обчислення, проте, дуже громіздкі, і корисно розглянути загальні результати, які виходять в трьох граничних випадках.
1) Випадок переважання резистивного розсіяння
Для кристала з великою кількістю дефектів всі моди сильно розсіваються унаслідок резистивних процесів; тоді для всіх мод τN
>> τR
, отже, τC
≈ τR
. У такому разі ϰ2
<< ϰ1
(якісно
це можна зрозуміти, припустивши, що всі часи релаксації не залежать від частоти, тому при порівнянні ϰ1
та ϰ2
інтеграли скорочуються і ми маємо ϰ2
/ ϰ1
= τR
/τN
<< 1). Пізніше буде видно, що це порівняльно простий вираз придатний для аналізу експериментальних даних по теплопровідності не дуже ідеальних кристалів.
2) Випадок переважання N-процесів за наявності резистивного розсіяння

В цьому випадку час релаксації τC
головним чином визначається N-процесами; тоді τR
>> τN
і τC
≈ τN
. Звідси легко побачити, що ϰ2
>> ϰ1
(якісно це можна зрозуміти, припустивши незалежність часів релаксації від частоти, і отримати ϰ/ϰ1
= τR
/τN
>> 1). Для коефіцієнта теплопровідності тоді маємо
Перш за все дивно, що формула (4.1.2), яка визначає теплопровідність у разі переважання N-процесів, не містить τN
. Проте N-процеси впливають на розподіл фононів і приводять його до форми (3.1). Коли N-процеси грають домінуючу роль, розподіл фононів стає «зміщеним» і не залежить від інтенсивності N-процесів. Тепловий опір виникає внаслідок резистивних процесів, що діють на цей розподіл.
Інший цікавий аспект формули (4.1.2) видно, якщо з її допомогою записати тепловий опір:
 (4.1.3) (4.1.3)
Для певного кристала при заданій температурі знаменник виразу (4.1.3) постійний. Оскільки  – сума швидкостей розсіяння для всіх типів резистивних процесів, то видно, що – сума швидкостей розсіяння для всіх типів резистивних процесів, то видно, що  , де Wi
– тепловий опір, відповідний кожному резистивному процесу i
, що діє окремо, але за умови переважання N-процесів. У загальному випадку тепловий опір неаддитивний, оскільки у формулі для ϰ1
швидкості релаксації складаються в знаменнику інтеграла (комбінований релаксаційний час
міститься в чисельнику), а, крім того (за винятком розглянутого тут граничного випадку), формула для ϰ2
дуже складна і не приводить до такого простого результату. , де Wi
– тепловий опір, відповідний кожному резистивному процесу i
, що діє окремо, але за умови переважання N-процесів. У загальному випадку тепловий опір неаддитивний, оскільки у формулі для ϰ1
швидкості релаксації складаються в знаменнику інтеграла (комбінований релаксаційний час
міститься в чисельнику), а, крім того (за винятком розглянутого тут граничного випадку), формула для ϰ2
дуже складна і не приводить до такого простого результату.
 Представляючи функції від ϰ, що входять в (4.1.3), через С(
ϰ)
і повну теплоємність С
і проводячи прості арифметичні дії, запишемо вираз (4.1.3) у вигляді Представляючи функції від ϰ, що входять в (4.1.3), через С(
ϰ)
і повну теплоємність С
і проводячи прості арифметичні дії, запишемо вираз (4.1.3) у вигляді
(4.1.4.а
)
Слід порівняти вираз (4.1.4.а
) з виразом для теплопровідності, отриманим релаксаційним методом у відсутність N-процесів. В цьому випадку час релаксації
кожної моди множиться на її внесок в теплоємність, а потім інтегрується по всіх модах для отримання теплопровідності
. Якщо ж переважають N-процеси, то швидкість
релаксації кожної моди множиться на її внесок в теплоємність і після інтеграції виходить повний тепловий опір
. В останньому випадку квадрат теплоємності в знаменнику виразу (4.1.4.а
) приводить до теплового опору, зворотного теплоємності, і до теплопровідності, пропорційній першому ступеню теплоємності.
Оскільки υ
τ = l
. можна у вираз (4.1.4.а
) ввести середню довжину вільного пробігу:
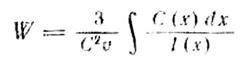
(4.1.4.б
)
Варіаційний метод у разі переважання N-процесів дає той же результат, тобто вирази (4.1.4.а
) і (4.1.4.б
).
Існує серія експериментів, в яких досліджувався вплив дефектів, причому для пояснення їх можна прямо застосувати розглянуту тут теорію.
У одному випадку метод Каллуея не знаходить застосування. Якщо резистивне розсіяння має місце тільки на межах кристала, а N-процеси відбуваються достатньо часто, то у виразі (4.1.4.а
) не можна представляти значення υ/D
для  (D – відповідний лінійний розмір кристала). Якщо проте це зробити, то отримаємо (D – відповідний лінійний розмір кристала). Якщо проте це зробити, то отримаємо

Останній вираз представляє якраз опір внаслідок розсіяння на межах у відсутність N-процесів, а отже, виходить, що N-процеси в даному випадку не грають ніякої ролі. Насправді для цієї спеціальної комбінації розсіяння теплопровідність перевищує
величину теплопровідності, отриману при розсіянні на межах у відсутність N-процесів, в число разів, рівне швидкості релаксації для N-процесів.
3) Випадок наявності тільки N-процесів
Оскільки на практиці досяжні тільки два попередні граничні випадки, тут ми покажемо, що в даному випадку результат виходить правдоподібним. Припустимо, що резистивні процеси відсутні зовсім, тому τ → ∞ і τС
= τN
. Знаменник ϰ2
тоді обертається на нуль, і ϰ2
→ ∞, тобто отримуємо нескінченну теплопровідність, що і потрібно було довести.
3.2 Варіаційний метод
Якщо розсіяння відбувається як внаслідок резистивних процесів, так і внаслідок N-процесів, чисельник варіаційного виразу для теплового опору складається з сум або інтегралів, відповідних кожному механізму розсіяння; для двох випадків маємо два вирази. Хоча при тих обставинах, яким відповідають чисельники цих виразів, можна точно отримати 1/ϰ = О, проте не можна написати простий вираз для теплового опору в загальному випадку, коли діють спільно декілька типів резестивного розсіяння, а також існують (або не існують) N-процеси. Ідея розгляду буде продемонстрована на прикладі методу Шерда і Займана для обчислення теплопровідності при розсіянні на точкових дефектах і наявності N-процесів. Розгляд приводить до тих же результатів, що і метод Каллуея.
1) Резистивні процеси і N-процеси однаково важливі
Для ілюстрації варіаційного розгляду в цьому загальному випадку передбачається, що резистивне розсіяння відбувається тільки на точкових дефектах; тим самим зменшується число членів, які потрібно враховувати. Це припущення було використане Шердом і Займаном для пояснення експериментальних результатів по розсіянню фононів ізотопічними «домішками».
Для випадку, коли пружне розсіяння на точкових дефектах відбувається одночасно з N-процесами, варіаційний вираз для теплового опору має вигляд

(4.2.1)
де функція  (q) повинна бути вибрана так, щоб мінімізувати цей опір. (q) повинна бути вибрана так, щоб мінімізувати цей опір.
Раніше було показано, що можна вибрати такий простий вид функції  (q), при якому перший або другий член в чисельнику звертається в нуль. Проте тепер при будь-якому виді (q), при якому перший або другий член в чисельнику звертається в нуль. Проте тепер при будь-якому виді  (q) один із членів у виразі (4.2.1) істотно відрізнятиметься від нуля. Дуже важко знайти точний вираз для (q) один із членів у виразі (4.2.1) істотно відрізнятиметься від нуля. Дуже важко знайти точний вираз для  (q), який привів би до мінімального можливого значення W
. Тому Шерд і Займан узяли правдоподібну комбінацію двох виразів для (q), який привів би до мінімального можливого значення W
. Тому Шерд і Займан узяли правдоподібну комбінацію двох виразів для  (q). Оскільки швидкість релаксації при розсіянні на точкових дефектах стрімко збільшується із зростанням q
, вони припустили, що починаючи з деякого значення q
розподіл фононів визначається дефектами та N-процесами, що вносять внесок в (q). Оскільки швидкість релаксації при розсіянні на точкових дефектах стрімко збільшується із зростанням q
, вони припустили, що починаючи з деякого значення q
розподіл фононів визначається дефектами та N-процесами, що вносять внесок в  (q
) незалежно один від одного. Для малих q
точкові дефекти самі по собі приводять до сильного відхилення від рівноважного розподілу, причому передбачалося, що їх внесок в (q
) незалежно один від одного. Для малих q
точкові дефекти самі по собі приводять до сильного відхилення від рівноважного розподілу, причому передбачалося, що їх внесок в  (q
) відповідає граничному значенню. Пробна функція, таким чином, була вибрана різною для двох інтервалів q
. (q
) відповідає граничному значенню. Пробна функція, таким чином, була вибрана різною для двох інтервалів q
.

Величина ε вважалася залежною від концентрації дефектів, але не залежною від температури. Шляхом варіювання коефіцієнтів а
0
і а
4
, а також величини ε знаходилося мінімальне значення теплового опору, який визначається виразом (4.2.1).
Можна очікувати, що інтервал значень q
, в якому на фононний розподіл істотно впливають точкові дефекти, збільшується при зростанні швидкості релаксації за рахунок розсіяння на точкових дефектах. При цьому значення q0
і ε повинні зменшуватися. Обчислення Шерда і Займана показали, що для малих концентрацій ізотопічних «домішок» у фториді літію (теорія була спочатку розвинена для пояснення експериментів на таких кристалах) ε ≈ 3, але для кристалів із значним розсіянням на точкових дефектах ε < 0,5.
У своїй першій роботі по застосуванню простого релаксаційного методу Клеменс враховував N-процеси, припускаючи, що вони усувають розбіжність ефективного часу релаксації при малих q
; час релаксації для фононів при q
< kв
T/
ħυ
рівний часу релаксації при q
= kв
T/
ħυ
= q0
. Теплопровідність визначається виразами з урахуванням цієї зміни, так що інтеграл розбивається на дві частини: для значень q
від 0 до q
0
час релаксації постійний, але від q
0
до q
макс
він залежить від q
звичайним способом.
Хоча може здатися, що процедура «обрізання», введена Клеменсом, неістотно відрізняється від методу Шерда і Займана, чисельні результати для багатьох випадків досить різні. Якщо переважають N-процеси, то рівноважний розподіл фононів порушується в широкій області q
і перший член в чисельнику виразу (4.2.1) стає великим. У межі, коли розподіл фононів головним чином визначається N-процесами, тепловий опір, обумовлений точковими дефектами, в 55 разів більше, ніж той, що дається формулою Клеменса, яка не враховує впливу N-процесів на розподіл фононів при q
> kв
T/
ħυ
. При концентрації точкових дефектів, відповідній значенню ε = 3, тепловий опір в 20 разів більше значення, яке обчислюється формулою Клеменса. З іншого боку, коли точкові дефекти значно важливіші і визначають розподіл навіть при значеннях q
< ½ kв
T/
ħυ
, є широка область фононів, для якої внеском першого члена у виразі (4.2.1) можна знехтувати, і тоді опір тільки трохи більший половини значення Клеменса.
2) N-процеси домінують за наявності резистивних процесів
У цьому граничному випадку передбачається, що розподіл фононів встановлюється тільки за рахунок N-процесів, а розсіяння на дефектах не міняє цього розподілу. У варіаційний вираз N-процеси, таким чином, не дають внеску. Для даного виду  (q
) знаменник виразу можна записати в простій формі. Через те що (q
) знаменник виразу можна записати в простій формі. Через те що

і
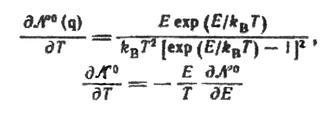
Знаменник має вигляд

де величина |u
| прийнята рівною 1, оскільки u
2
міститься і в чисельнику, і в знаменнику. Коли має місце ізотропне розсіяння і вірогідність P
(q, q') залежить тільки від відносної орієнтації q
та q'
, чисельник також набуває простій вигляд, і, замінюючи суму інтегруванням, його можна записати у такому вигляді

Тепловий опір тоді визначається формулою

яка співпадає з виразом Каллуея в тій же межі переважання N-процесів.
Слід відмітити, що якщо τ(q
) ~ q
-4
, як у разі точкових дефектів, то й вираз для теплопровідності залишається кінцевим, оскільки інтеграл має
Вигляд

і сходиться на обох межах. Якщо розсіяння менш сильно залежить від q
, наприклад τ(q
) ~ q
-1
, то простий релаксаційний метод дає кінцеву теплопровідність; збільшення часу релаксації із зменшенням q
не врівноважує зменшення внеску цих мод в теплопровідність, яка визначається енергією фононів і щільністю станів, пропорційною q
2
. Вираз для ϰ, отриманий простим релаксаційним методом, містить тоді

тоді як варіаційний вираз або формула Каллуея при домінуванні N-процесів містить
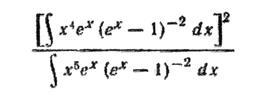
Всі ці інтеграли досягають граничних значень при дуже малих х
, і відношення χрел
/χN
дом
стає рівним 1,3. Як видно, резистивне розсіяння все ще грає важливу роль для малих значень q
, але внесок від домінуючих N-процесів сильно не збільшує теплового опору.
3.3 Метод Гюйе і Крумхансла
Серед методів, заснованих на використанні рівняння Больцмана для фононів, заслуговує уваги робота Гюйе і Крумхансла по гідродинаміці фононів. Вона є порівняно раннім дослідженням загальних властивостей фононних систем. Передбачається, що розподіл фононів залежить від часу і координат. Зміна розподілу по ширині кристала, а також і уздовж його довжини при постійному температурному градієнті приводить до пуазейльовського протікання, тоді як зміна розподілу з часом дозволяє отримати другий звук, який є хвилевим процесом розповсюдження зміни N
.
Розгляд ведеться з використанням операторної форми для рівняння Больцмана, і загальні результати виражаються через оператори зіткнень, причому розрізняються оператори для нормального розсіяння N
* і для резистивного розсіяння R
*. Вирішення рівняння Больцмана і, отже, виразу для потоку тепла і теплопровідності записуються через цих операторів, тому необхідно тільки виразити останні через швидкості релаксації  і і  , щоб довести відповіді до числових результатів. , щоб довести відповіді до числових результатів.
За умови N
* > R
*, відповідному  >> >>  , теплопровідність виходить та ж, що і визначувана другим членом виразу Каллуея; отже, вона співпадає з величиною, знайденою варіаційним методом при переважанні N-процесів. За умови R
* > N
*, відповідному , теплопровідність виходить та ж, що і визначувана другим членом виразу Каллуея; отже, вона співпадає з величиною, знайденою варіаційним методом при переважанні N-процесів. За умови R
* > N
*, відповідному  >> >>  , виходить той же вираз для теплопровідності, що і при простому релаксаційному методі; тут вона також співпадає з першим членом у виразі Каллуея. , виходить той же вираз для теплопровідності, що і при простому релаксаційному методі; тут вона також співпадає з першим членом у виразі Каллуея.
Гюйе і Крумхансл приводять вираз, справедливий для всього інтервалу відносних значень  і і  : :

(4.3.1)

де
а  – таке ж середнє для [τR
(х
)]-1
. Величина S
рівна – таке ж середнє для [τR
(х
)]-1
. Величина S
рівна  / /  і називається чинником перемикання. Якщо і називається чинником перемикання. Якщо  << << 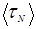 , тo величина S
велика і в дужках виразу (3.3.1) найбільш важливий член , тo величина S
велика і в дужках виразу (3.3.1) найбільш важливий член  . Peзистивні процеси тоді переважають, і теплопровідність виходить така ж, як при використанні простого релаксаційного методу. У разі τR
>> τN
величина S
мала і головну роль грає член . Peзистивні процеси тоді переважають, і теплопровідність виходить така ж, як при використанні простого релаксаційного методу. У разі τR
>> τN
величина S
мала і головну роль грає член  -
1
. Нормальні процеси визначають розподіли фононів, і вираз для теплопровідності співпадає з формулою Займана і Каллуея для цього граничного випадку, а тепловий опір аддитивний. -
1
. Нормальні процеси визначають розподіли фононів, і вираз для теплопровідності співпадає з формулою Займана і Каллуея для цього граничного випадку, а тепловий опір аддитивний.
У проміжній області відносних значень τR
і τN
швидкості розсіяння, що отримуються при аналізі експериментів за допомогою виразів Каллуея і Гюйе – Крумхансла, дуже близькі, але погодження дещо гірше, якщо  ≈ ≈  -1
. -1
.
висновки
Одним з ефектів, що обумовлений ангармонічним характером коливань атомів, є тепловий опір твердих тіл. Він не міг б виникнути, якби атоми здійснювали строго гармонійні коливання, що розповсюджуються в решітках у вигляді системи пружних хвиль, що не взаємодіють між собою. Відсутність взаємодії між хвилями дозволяла б їм розповсюджуватися в кристалі не розсіваючись, тобто не зустрічаючи ніякого опору, подібно до розповсюдження світла в порожнечі.
Якби в такому кристалі можна було створити різницю температур, то атоми гарячого кінця, що коливаються з великими амплітудами, передавали б свою енергію сусіднім атомам і фронт теплової хвилі розповсюджувався б уздовж кристала із швидкістю звуку. Оскільки ця хвиля не зустрічала б ніякого опору, то навіть при нескінченно малій різниці температур тепловий потік міг би досягати якої завгодно великої величини; теплопровідність такого кристала була б нескінченно великою.
У реальних кристалах при не дуже низьких температурах коливання атомів носять ангармонічний характер. Поява ангармонічності призводить до того, що нормальні коливання решіток втрачають незалежний характер і при зустрічах взаємодіють один з одним, обмінюючись енергією і змінюючи напрям свого розповсюдження (розсіваючись один на одному). Саме внаслідок протікання таких процесів взаємодії пружних хвиль стає можливою передача енергії від коливань однієї частоти до коливань іншої частоти і встановлення в кристалі теплової рівноваги.
Опис процесу розсіяння нормальних коливань один на одному зручно вести на мові фононів, розглядаючи термічно збуджений кристал як ящик, заповнений фононами. У гармонійному наближенні, в якому нормальні коливання решіток є незалежними, фонони утворюють ідеальний газ (газ невзаємодіючих фононів). Перехід до ангармонічних коливань еквівалентний введенню взаємодії між фононами, в результаті якої можуть відбуватися процеси розщеплювання фонона на два і більш і утворення одного фонона з двох. Такі процеси прийнято називати фонон-фононним розсіянням
.
Всі процеси розсіяння, внаслідок якого розподіл фононів прагне до рівноважного, прямо впливають на теплопровідність. Для більшості процесів інтенсивність розсіяння залежить від частоти фононів, і N-процеси грають важливу роль, перерозподіляючи енергію між різними модами і тим самим перешкоджаючи сильному відхиленню від рівноважної населеності в кожній моді. Взагалі кажучи, важко виділити внесок від N-процесів, і необхідний досить докладний аналіз експериментальних результатів, щоб зрозуміти, як позначаються N-процеси на теплопровідності. Проте у ряді випадків їх вплив дуже істотний.
список використаної літератури
1. Берман Р. Теплопроводность твердых тел. – М.: Высшая школа, 1979.
2. Бушманов Б.Н., Хромов Ю.А. Физика твердого тела. – Учебн. пособие для втузов. – М.: Высшая школа, 1975. – 224 с.
3. Епифанов Г.И. Физика твердого тела. Учеб. пособие для втузов. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1979. – 288 с.
4. Жданов Г.С. Физика твердого тела. – М.: МГУ, 1971.
5. Займан Дж. Принципы теории тевердого тела. – М.: «Мир», 1976.
6. Киттель Ч. Введение в физику твердого тела. – М.: Физматгиз, 1973.
7. Китель Ч. Элементарная физика твердого тела. – М.: «Наука», 1985.
8. Курик М.В., Цмоць В.М. Фізика твердого тіла. – К.: Вища школа. Головне видавництво, 1985. – 246 с.
9. Мартон К., Смит. Основы физики металлов. – М.: Металлургиздат, 1972.
10. Най Дж. Физические свойства кристаллов. – М., ИЛ, 1986.
11. Полежаев Ю.В. Теплопроводность. Физич. словарь. Т. 5. – 1987.
12. Спроул Р. Современная физика. – М.: Физматгиз, 1981.
13. Твердое тело. Структура и свойства. – М.: «Знание», «Физики и физике», 1972.
14. Уэрт Ч., Томсон Р. Физика твердого тела. – М.: «Мир», 1986.
|