Контрольная работа: Дифференциальные уравнения

Задача №1

Даны вершины треугольника АВС.

Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.

А(-7;5), В(5;-4), С(3;10).

Решение

1. Расстояние d между точками M₁ (x₁ ;у₁ ) и М₂ (х₂ ;у₂ ) определяется по формуле:

Подставив в эту формулу координаты точек А и В имеем:

2. Уравнение прямой, проходящей через точки М₁ (х₁ ;у₁ ) и М₂ (х₂ ;у₂ ), имеет вид:

Подставив в формулу (2) координаты точек А и В, получим уравнение прямой АВ:

Для нахождения углового коэффициента k_ab прямой АВ разрешим полученное уравнение относительно у:

Отсюда

k_ab = - 3/4.

Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС.

Для нахождения углового коэффициента k_aс прямой АС разрешим полученное уравнение относительно у:

Отсюда

k_aс = 1/2.

3. Угол α между двумя прямыми, угловые коэффициенты которых равны k₁ и k₂ , определяется по формуле:

Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее

k₁ = k_ab = -3/4, k₂ = k_ac = 1/2.

< А = arctg 2 = 1,11 рад.

4. Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

Уравнение прямой, проходящей через данную точку М₁ (х₁ ;у₁ ) в заданном угловом коэффициенте k имеет вид:

у – у₁ = k(х – х₁ ).(4)

Подставив в формулу (4) координаты точки С и k_cd = 4/3, получим уравнение высоты CD:

у – 10 = 4/3(х – 3) , у – 10 = 4/3х – 4 , 4х – 3у + 18 = 0. (CD)

Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (СD):

Подставив в формулу (1) координаты точек C и D, находим:

СD= √(-3 -3)² + (2 -10)² = √36 + 64 = 10 .

5. Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:

(х – а)² + (у – b)² = R² (5)

Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим:

Следовательно E(0;6) и R = CD/2 = 5. Используя формулу (5), получим уравнение искомой окружности:

(х – 0)² + (у – 6)² = 25, х² + (у – 6)² = 25.

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая прямая ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В. Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:

3* 3+ 4*10 +1 = 50 > 0.

поэтому искомое неравенство имеет вид:

3х + 4у +1 ≥ 0.

Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:

Подставив в последнее уравнение координаты точки А, имеем:

7* (- 7) + 5 – 31 = - 75 < 0.

Искомое неравенство будет

7х + у – 31 ≤ 0.

Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В:

5 – 2(- 4) + 17 = 30 > 0.

Третье искомое неравенство

х – 2у + 17 ≥ 0.

Итак, множество точек треугольника АВС определяется системой неравенств:

Задача №2

Даны векторы a₁ , a₂ , a₃ , b . Показать, что векторы a₁ , a₂ , a₃ образуют базис трехмерного пространства и найти координаты вектора b в этом базисе.

a₁ (5;3;1) , а₂ (-2;-1;2) , а₃ (-2;1;4) , b(3;0;1)

Решение

1. Система векторов в пространстве Rⁿ линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются координаты векторов системы:

Подставив в формулу (1) координаты векторов a₁ , a₂ , a₃ найдем определитель:

Так как определитель не равен нулю, то данные три вектора являются линейно независимыми. Соответственно они образуют базис трехмерного пространства.

2. Вычислим координаты вектора b в новом базисе. А – матрица перехода.

b = А * b_new

Нам необходимо определить координаты b_new .

b_new = A^-1 * b(2)

Для нахождения обратной матрицы применяется формула

Необходимо найти все элементы для составления обратной матрицы:

Подставляем полученные элементы в формулу (3) и найдем А^-1 :

Подставив значения А^-1 и вектора b в формулу (2), найдем координаты вектора b в новом базисе:

Задача №3

Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

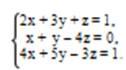
Решение

Обозначим через матрицу А – матрицу коэффициенты при неизвестных; Х – матрицу-столбец неизвестных Х, У, Z_; H – матрицу-столбец свободных членов:

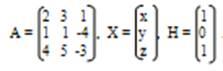
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:

А*Х = Н(1)

Если матрица А – невырожденная (ее определитель Δ отличен от нуля), то она имеет обратную матрицу А^-1 . Умножив обе части уравнения (1) на А^-1 , получим:

А^-1 * А * Х = А^-1 * Н

Но А^-1 * А = Е (Е- единичная матрица), а ЕХ = Х, поэтому

Х = А^-1 * Н(2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А^-1 .

Пусть имеем невырожденную матрицу

где А_ij (i=1,2,3; j=1,2,3) – алгебраическое дополнение элемента а_ij в определителе матрицы А, которое является произведением (- 1)^ij на минор (определитель) второго- порядка, полученный вычеркиванием i-строки и j-столбца в определителе матрицы А.

Вычислим определитель Δ и алгебраические дополнения А_ij элементов матрицы А.

Следовательно матрица А имеет обратную матрицу А^-1 .

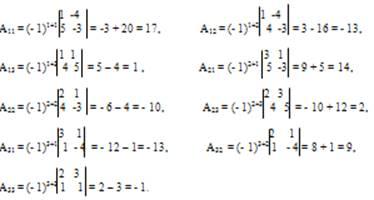
Тогда

По формуле (2) находим решение данной системы уравнений в матричной форме:

Отсюда

х = - 1; у = 1; z = 0.

Задача №4

Вычислить пределы.

Решение

а) Подстановка предельного значения аргумента х = 3 приводит к неопределенному выражению вида .

Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим на множитель (х – 3). Такое сокращение здесь возможно, так как множитель (х – 3) отличен от нуля при х →3:

б) При х→∞ выражение дает неопределенность вида . Для устранения этой неопределенности применим правило Лопиталя. Для разыскания предела отношения двух функций, бесконечно больших при х→∞, можно рассматривать отношение их производных .Если оно стремится к пределу (конечному или бесконечному), то к тому же пределу стремится и отношение .

в) Обозначим arctg 3х = у. Тогда 3х = tg у и у→0 при х→0. Применяя свойства пределов и формулу первого замечательного предела lim sin α/ α = 1, имеем:

г)При х→∞ выражение 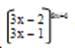является неопределенностью вида 1^∞ . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при х→∞ величины и применим формулу второго замечательного предела:

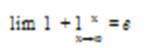
Тогда имеем:

Пусть 3х – 1 = - у . Тогда 6х + 4 = - 2у + 6 и у→ -∞ при х→∞. Переходя к переменной у, получим:

Задача №5

Найти производные функций:

Решение

а) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной у′ нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно у′ .

3у² у′ + е^ху (у + ху′) = 0, 3у² у′ + уе^ху + хе^ху у′ = 0,

Из последующего уравнения находим у′:

у′ (3у² + хе^ху ) + уе^ху = 0,

Задача №6

Исследовать функцию методами дифференциального исчисления и построить ее график. Исследование функции рекомендуется проверить по следующей схеме:

1) найти область определения функции;

2) исследовать функцию на непрерывность;

3) определить, является ли данная функция четной, нечетной;

4) найти интервалы возрастания и убывания функции и точки ее экстремума;

5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба;

6) найти асимптоты графика функции.

Решение

1. Функция определена при всех значениях аргумента х.

2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервале (- ∞; ∞).

3. Для установления четности и нечетности функции проверим выполнимость равенств f(- х) = f( х) (тогда f( х) – четная функция) или f(-x) = - f(х) (для нечетной функции) для любых х и – х из области определения функции:

Следовательно, f(-х) ≠ f(x) и f(-х) ≠ -f(х), то есть данная функция не является ни четной, ни нечетной.

4. Для исследования функции на экстремум найдем ее первую производную:

у′ = 0 при х₁ = - 3, х₂ = 3. Тем самым имеем две критические точки, обе принадлежать области определения функции.

Разобьем числовую ось на три интервала: (- ∞; - 3), (- 3; 3), (3; ∞).

В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает, во втором интервале – положительна и данная функция возрастает. При переходе через точку х = -3 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:

у_min = у(-3) = 0

Значит, А(-3;0) – точка минимума.

При переходе через точку х = 3 первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум:

у_max = у(3) = 2

Значит, В(3;2) – точка максимума.

На рис. 1 знаками +, - указаны интервалы знакопостоянства производной у′, а стрелками – возрастание и убывание исследуемой функции.

5. Для определения точек перегиба графика и интервалов выпуклости и вогнутости кривой найдем вторую производную:

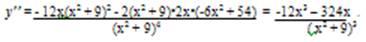
у′′ = 0 при х₁ = 0, х₂ = - 3√3 , х₃ = 3√3.

Разобьем числовую ось на четыре интервалы: (-∞;-3√3), (-3√3 ;0), (0;3√3), (3√3 ; ∞).

рис.2

На первом, втором и четвертом интервалах вторая производная у′′ положительна и дуга исследуемой кривой вогнута; на третьем интервале у′′ отрицательна – дуга выпукла.

При переходе через точки х = 0 у′′ меняет свой знак, поэтому х= 0 – абсцисса точки перегиба.

Следовательно С(0;1) – точка перегиба графика функции.

При переходе через точку х = 3√3 у′′ меняет свой знак, поэтому х= 3√3 - абсцисса точки перегиба.

Следовательно – точка перегиба графика функции.

6. Так как точек разрыва у данной функции нет, соответственно вертикальной асимптоты она не имеет. Для определения уравнения наклонной асимптоты у=kx + b воспользуемся формулами:

Тогда

При вычислении пределов использовалось правило Лопиталя.

у=kx + b, у= 0*х + 1 = 1

Значит прямая у=1 есть горизонтальная асимптота графика исследуемой функции.

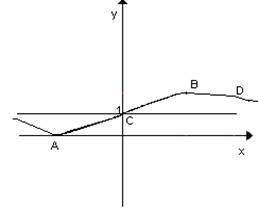
рис. 3

Задача №7

Найти неопределенные интегралы и результаты интегрирования проверить дифференцированием.

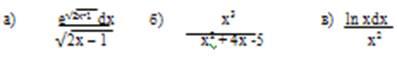
Решение

а) Применяя свойства неопределенного интеграла и формулы табличных интегралов имеем:

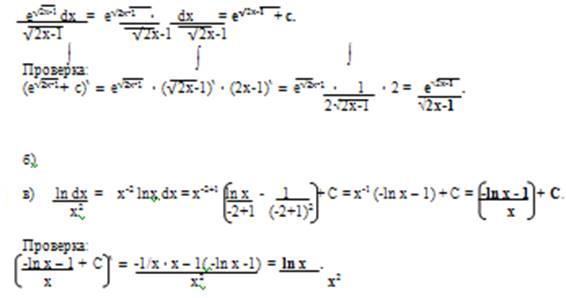
Задача №8

Вычислить объем тела, образованного вращением оси ОХ фигуры, ограниченной линиями ху=4; х=1; х=4; у=0. Сделать чертеж.

Решение

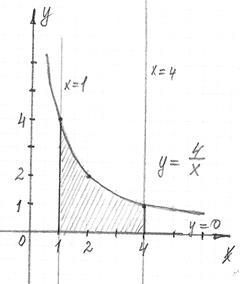
Объем тела, образованного вращением оси ОХ фигуры, ограниченной линиями определяется по формуле:

Подставим в формулу (1) у = 4/х, х₁ = 1, х₂ = 4, получим:

Ответ: объем тела вращения равен 12π