Задача №1.
Заполнить последовательность первых 20 членов последовательности, найти их сумму и произведение
| a1 |
a2 |
a3 |
| 1 |
2 |
5 |
| Решение
|
| n |
an |
Sn |
Pn |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
3 |
2,00 |
| 3 |
5 |
8 |
10,00 |
| 4 |
0,5 |
8,5 |
5,00 |
| 5 |
3,875 |
12,375 |
19,38 |
| 6 |
3,03125 |
15,40625 |
58,73 |
| 7 |
1,5546875 |
16,9609375 |
91,31 |
| 8 |
4,033203125 |
20,99414063 |
368,26 |
| 9 |
2,042480469 |
23,03662109 |
752,17 |
| 10 |
2,67199707 |
25,70861816 |
2009,79 |
| 11 |
3,378143311 |
29,08676147 |
6789,36 |
| 12 |
2,023323059 |
31,11008453 |
13737,06 |
| 13 |
3,187238693 |
34,29732323 |
43783,30 |
| 14 |
2,748459339 |
37,04578257 |
120336,61 |
| 15 |
2,423996806 |
39,46977937 |
291695,55 |
| 16 |
3,158659488 |
42,62843886 |
921366,93 |
| 17 |
2,483678035 |
45,1121169 |
2288378,80 |
| 18 |
2,77640784 |
47,88852474 |
6353472,83 |
| 19 |
2,916731674 |
50,80525641 |
18531375,45 |
| 20 |
2,521779528 |
53,32703594 |
46732043,24 |
Исходные данные вносятся в ячейки, выделенные черным цветом.
Пояснения.
В условии заданы три первых элемента прогрессии. Все остальные элементы вычисляются по рекуррентной формуле, т.е. через известные предыдущие элементы прогрессии. В нашей задаче получаем:

Сумму и произведение элементов прогрессии можно также вычислить по рекуррентной формуле:

Задача №2.
Вычислить значение функции y(x) в точках x1 и x2. Построить график этой функции на интервале [x1; x2] с шагом 0,1l; l – длина отрезка [x1; x2].
| точка x1
|
точка x2
|
функция
|
| -1,838 |
1,433 |
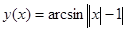
|
| решение
|
| x
|
y
|
| -1,838 |
0,993607623 |
| -1,5109 |
0,536231415 |
| -1,1838 |
0,184850925 |
| -0,8567 |
-0,14379503 |
| -0,5296 |
-0,489744005 |
| -0,2025 |
-0,92314005 |
| 0,1246 |
-1,066262671 |
| 0,4517 |
-0,580330072 |
| 0,7788 |
-0,22304478 |
| 1,1059 |
0,106098947 |
| 1,433 |
0,447818305 |
Исходные данные (x1
и x2
) вносятся ячейки, выделенные в образце черным цветом.
Пояснения.
В условии задан отрезок [x1
, x2
], на котором требуется построить график. Шаг выбирается таким образом, чтобы исходный отрезок разбивался на 10 равных частей.
Задача №3
Построить таблицу значений функции z (x, y) и её отображение в виде поверхности на области (x, y), принадлежащей [-1…1; – 1…1] с шагом 0,1 по каждому направлению
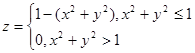
| Решение
|
| Таблица значений
|
| Ось х
|
| -1 |
-0,9 |
-0,8 |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
-0,2 |
-0,1 |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
| Ось у
|
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| -0,9 |
0 |
0 |
0 |
0 |
0 |
0 |
0,03 |
0,1 |
0,15 |
0,18 |
0,19 |
0,18 |
0,15 |
0,1 |
0,03 |
0 |
0 |
0 |
0 |
0 |
0 |
| -0,8 |
0 |
0 |
0 |
0 |
0 |
0,11 |
0,2 |
0,27 |
0,32 |
0,35 |
0,36 |
0,35 |
0,32 |
0,27 |
0,2 |
0,11 |
0 |
0 |
0 |
0 |
0 |
| -0,7 |
0 |
0 |
0 |
0,02 |
0,15 |
0,26 |
0,35 |
0,42 |
0,47 |
0,5 |
0,51 |
0,5 |
0,47 |
0,42 |
0,35 |
0,26 |
0,15 |
0,02 |
0 |
0 |
0 |
| -0,6 |
0 |
0 |
0 |
0,15 |
0,28 |
0,39 |
0,48 |
0,55 |
0,6 |
0,63 |
0,64 |
0,63 |
0,6 |
0,55 |
0,48 |
0,39 |
0,28 |
0,15 |
0 |
0 |
0 |
| -0,5 |
0 |
0 |
0,11 |
0,26 |
0,39 |
0,5 |
0,59 |
0,66 |
0,71 |
0,74 |
0,75 |
0,74 |
0,71 |
0,66 |
0,59 |
0,5 |
0,39 |
0,26 |
0,11 |
0 |
0 |
| -0,4 |
0 |
0,03 |
0,2 |
0,35 |
0,48 |
0,59 |
0,68 |
0,75 |
0,8 |
0,83 |
0,84 |
0,83 |
0,8 |
0,75 |
0,68 |
0,59 |
0,48 |
0,35 |
0,2 |
0,03 |
0 |
| -0,3 |
0 |
0,1 |
0,27 |
0,42 |
0,55 |
0,66 |
0,75 |
0,82 |
0,87 |
0,9 |
0,91 |
0,9 |
0,87 |
0,82 |
0,75 |
0,66 |
0,55 |
0,42 |
0,27 |
0,1 |
0 |
| -0,2 |
0 |
0,15 |
0,32 |
0,47 |
0,6 |
0,71 |
0,8 |
0,87 |
0,92 |
0,95 |
0,96 |
0,95 |
0,92 |
0,87 |
0,8 |
0,71 |
0,6 |
0,47 |
0,32 |
0,15 |
0 |
| -0,1 |
0 |
0,18 |
0,35 |
0,5 |
0,63 |
0,74 |
0,83 |
0,9 |
0,95 |
0,98 |
0,99 |
0,98 |
0,95 |
0,9 |
0,83 |
0,74 |
0,63 |
0,5 |
0,35 |
0,18 |
0 |
| 0 |
0 |
0,19 |
0,36 |
0,51 |
0,64 |
0,75 |
0,84 |
0,91 |
0,96 |
0,99 |
1 |
0,99 |
0,96 |
0,91 |
0,84 |
0,75 |
0,64 |
0,51 |
0,36 |
0,19 |
0 |
| 0,1 |
0 |
0,18 |
0,35 |
0,5 |
0,63 |
0,74 |
0,83 |
0,9 |
0,95 |
0,98 |
0,99 |
0,98 |
0,95 |
0,9 |
0,83 |
0,74 |
0,63 |
0,5 |
0,35 |
0,18 |
0 |
| 0,2 |
0 |
0,15 |
0,32 |
0,47 |
0,6 |
0,71 |
0,8 |
0,87 |
0,92 |
0,95 |
0,96 |
0,95 |
0,92 |
0,87 |
0,8 |
0,71 |
0,6 |
0,47 |
0,32 |
0,15 |
0 |
| 0,3 |
0 |
0,1 |
0,27 |
0,42 |
0,55 |
0,66 |
0,75 |
0,82 |
0,87 |
0,9 |
0,91 |
0,9 |
0,87 |
0,82 |
0,75 |
0,66 |
0,55 |
0,42 |
0,27 |
0,1 |
0 |
| 0,4 |
0 |
0,03 |
0,2 |
0,35 |
0,48 |
0,59 |
0,68 |
0,75 |
0,8 |
0,83 |
0,84 |
0,83 |
0,8 |
0,75 |
0,68 |
0,59 |
0,48 |
0,35 |
0,2 |
0,03 |
0 |
| 0,5 |
0 |
0 |
0,11 |
0,26 |
0,39 |
0,5 |
0,59 |
0,66 |
0,71 |
0,74 |
0,75 |
0,74 |
0,71 |
0,66 |
0,59 |
0,5 |
0,39 |
0,26 |
0,11 |
0 |
0 |
| 0,6 |
0 |
0 |
0 |
0,15 |
0,28 |
0,39 |
0,48 |
0,55 |
0,6 |
0,63 |
0,64 |
0,63 |
0,6 |
0,55 |
0,48 |
0,39 |
0,28 |
0,15 |
0 |
0 |
0 |
| 0,7 |
0 |
0 |
0 |
0,02 |
0,15 |
0,26 |
0,35 |
0,42 |
0,47 |
0,5 |
0,51 |
0,5 |
0,47 |
0,42 |
0,35 |
0,26 |
0,15 |
0,02 |
0 |
0 |
0 |
| 0,8 |
0 |
0 |
0 |
0 |
0 |
0,11 |
0,2 |
0,27 |
0,32 |
0,35 |
0,36 |
0,35 |
0,32 |
0,27 |
0,2 |
0,11 |
0 |
0 |
0 |
0 |
0 |
| 0,9 |
0 |
0 |
0 |
0 |
0 |
0 |
0,03 |
0,1 |
0,15 |
0,18 |
0,19 |
0,18 |
0,15 |
0,1 |
0,03 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| РЕШЕНИЕ
|
| Таблица значений
|
| Ось х
|
| 1 |
-1 |
-0,9 |
-0,8 |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
-0,2 |
-0,1 |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
| Ось у
|
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| -0,9 |
0 |
0 |
0 |
0 |
0 |
0 |
0,03 |
0,1 |
0,15 |
0,18 |
0,19 |
0,18 |
0,15 |
0,1 |
0,03 |
0 |
0 |
0 |
0 |
0 |
0 |
| -0,8 |
0 |
0 |
0 |
0 |
0 |
0,11 |
0,2 |
0,27 |
0,32 |
0,35 |
0,36 |
0,35 |
0,32 |
0,27 |
0,2 |
0,11 |
0 |
0 |
0 |
0 |
0 |
| -0,7 |
0 |
0 |
0 |
0,02 |
0,15 |
0,26 |
0,35 |
0,42 |
0,47 |
0,5 |
0,51 |
0,5 |
0,47 |
0,42 |
0,35 |
0,26 |
0,15 |
0,02 |
0 |
0 |
0 |
| -0,6 |
0 |
0 |
0 |
0,15 |
0,28 |
0,39 |
0,48 |
0,55 |
0,6 |
0,63 |
0,64 |
0,63 |
0,6 |
0,55 |
0,48 |
0,39 |
0,28 |
0,15 |
0 |
0 |
0 |
| -0,5 |
0 |
0 |
0,11 |
0,26 |
0,39 |
0,5 |
0,59 |
0,66 |
0,71 |
0,74 |
0,75 |
0,74 |
0,71 |
0,66 |
0,59 |
0,5 |
0,39 |
0,26 |
0,11 |
0 |
0 |
| -0,4 |
0 |
0,03 |
0,2 |
0,35 |
0,48 |
0,59 |
0,68 |
0,75 |
0,8 |
0,83 |
0,84 |
0,83 |
0,8 |
0,75 |
0,68 |
0,59 |
0,48 |
0,35 |
0,2 |
0,03 |
0 |
| -0,3 |
0 |
0,1 |
0,27 |
0,42 |
0,55 |
0,66 |
0,75 |
0,82 |
0,87 |
0,9 |
0,91 |
0,9 |
0,87 |
0,82 |
0,75 |
0,66 |
0,55 |
0,42 |
0,27 |
0,1 |
0 |
| -0,2 |
0 |
0,15 |
0,32 |
0,47 |
0,6 |
0,71 |
0,8 |
0,87 |
0,92 |
0,95 |
0,96 |
0,95 |
0,92 |
0,87 |
0,8 |
0,71 |
0,6 |
0,47 |
0,32 |
0,15 |
0 |
| -0,1 |
0 |
0,18 |
0,35 |
0,5 |
0,63 |
0,74 |
0,83 |
0,9 |
0,95 |
0,98 |
0,99 |
0,98 |
0,95 |
0,9 |
0,83 |
0,74 |
0,63 |
0,5 |
0,35 |
0,18 |
0 |
| 0 |
0 |
0,19 |
0,36 |
0,51 |
0,64 |
0,75 |
0,84 |
0,91 |
0,96 |
0,99 |
1 |
0,99 |
0,96 |
0,91 |
0,84 |
0,75 |
0,64 |
0,51 |
0,36 |
0,19 |
0 |
| 0,1 |
0 |
0,18 |
0,35 |
0,5 |
0,63 |
0,74 |
0,83 |
0,9 |
0,95 |
0,98 |
0,99 |
0,98 |
0,95 |
0,9 |
0,83 |
0,74 |
0,63 |
0,5 |
0,35 |
0,18 |
0 |
| 0,2 |
0 |
0,15 |
0,32 |
0,47 |
0,6 |
0,71 |
0,8 |
0,87 |
0,92 |
0,95 |
0,96 |
0,95 |
0,92 |
0,87 |
0,8 |
0,71 |
0,6 |
0,47 |
0,32 |
0,15 |
0 |
| 0,3 |
0 |
0,1 |
0,27 |
0,42 |
0,55 |
0,66 |
0,75 |
0,82 |
0,87 |
0,9 |
0,91 |
0,9 |
0,87 |
0,82 |
0,75 |
0,66 |
0,55 |
0,42 |
0,27 |
0,1 |
0 |
| 0,4 |
0 |
0,03 |
0,2 |
0,35 |
0,48 |
0,59 |
0,68 |
0,75 |
0,8 |
0,83 |
0,84 |
0,83 |
0,8 |
0,75 |
0,68 |
0,59 |
0,48 |
0,35 |
0,2 |
0,03 |
0 |
| 0,5 |
0 |
0 |
0,11 |
0,26 |
0,39 |
0,5 |
0,59 |
0,66 |
0,71 |
0,74 |
0,75 |
0,74 |
0,71 |
0,66 |
0,59 |
0,5 |
0,39 |
0,26 |
0,11 |
0 |
0 |
| 0,6 |
0 |
0 |
0 |
0,15 |
0,28 |
0,39 |
0,48 |
0,55 |
0,6 |
0,63 |
0,64 |
0,63 |
0,6 |
0,55 |
0,48 |
0,39 |
0,28 |
0,15 |
0 |
0 |
0 |
| 0,7 |
0 |
0 |
0 |
0,02 |
0,15 |
0,26 |
0,35 |
0,42 |
0,47 |
0,5 |
0,51 |
0,5 |
0,47 |
0,42 |
0,35 |
0,26 |
0,15 |
0,02 |
0 |
0 |
0 |
| 0,8 |
0 |
0 |
0 |
0 |
0 |
0,11 |
0,2 |
0,27 |
0,32 |
0,35 |
0,36 |
0,35 |
0,32 |
0,27 |
0,2 |
0,11 |
0 |
0 |
0 |
0 |
0 |
| 0,9 |
0 |
0 |
0 |
0 |
0 |
0 |
0,03 |
0,1 |
0,15 |
0,18 |
0,19 |
0,18 |
0,15 |
0,1 |
0,03 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Поверхность

Задача №4
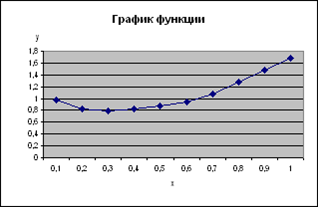
Построить график функции y(x) на заданном интервале, согласно поставленным условиям
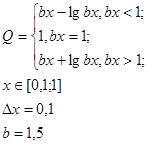
| Таблица y(x) |
| x |
y |
 |
| 0,1 |
0,973909 |
| 0,2 |
0,822879 |
| 0,3 |
0,796787 |
| 0,4 |
0,821849 |
| 0,5 |
0,874939 |
| 0,6 |
0,945757 |
| 0,7 |
1,071189 |
| 0,8 |
1,279181 |
| 0,9 |
1,480334 |
| 1 |
1,676091 |
Пояснения:
При нахождении значений графика относительно оси у
мы должны учитывать ограничения, заданные условием.
Задачи общего типа
7. Задача №1 (общая)
Таблица чисел.
Ниже таблицы необходимо вычислить:
· сумму всех чисел таблицы,
· среднее арифметическое всех чисел таблицы,
· максимальное число в таблице,
· минимальное число в таблице.
Значения: х – от 1 до 31 с шагом 2;
у – от 2 до 32 с шагом 2;
z – среднее арифметическое соответствующих х и у.
| Таблица чисел
|
| x |
y |
z |
| 1 |
2 |
1,5 |
| 3 |
4 |
3,5 |
| 5 |
6 |
5,5 |
| 7 |
8 |
7,5 |
| 9 |
10 |
9,5 |
| 11 |
12 |
11,5 |
| 13 |
14 |
13,5 |
| 15 |
16 |
15,5 |
| 17 |
18 |
17,5 |
| 19 |
20 |
19,5 |
| 21 |
22 |
21,5 |
| 23 |
24 |
23,5 |
| 25 |
26 |
25,5 |
| 27 |
28 |
27,5 |
| 29 |
30 |
29,5 |
| 31 |
32 |
31,5 |
| Сумма
|
792 |
| Среднее ариф.
|
16,5 |
| Максимальное
|
32 |
| Минимальное
|
1 |
Пояснения:
Сумма = СУММ столбца x)
Среднее значение = СРЗНАЧ (все значений)
Максимальное = МАКС (все значений)
Минимальное = МИН (всех значений)
Задача №2.1 (общая)
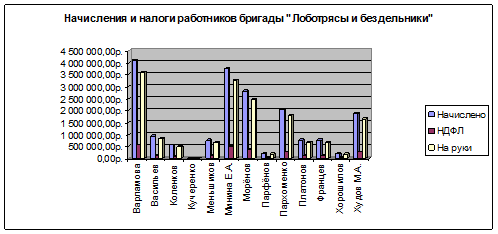
Необходимо рассчитать КТУ, сколько начислено каждому работнику, НДФЛ и сколько выдано на руки каждому работнику. В конце нужно посчитать, сколько составляет заработная плата всей бригады, построить гистограмму, основанную на данных вычислениях.
| Расчет заработной платы бригады «Лоботрясы и бездельники»
|
| № п/п
|
Ф.И.О.
|
КТУ
|
Начислено
|
НДФЛ
|
На руки
|
| 1 |
Варламова Д.А. |
22,00% |
4 108 476,02 р. |
534 101,88 р. |
3 574 374,14 р. |
| 2 |
Васильев М.Ю. |
5,00% |
933 744,55 р. |
121 386,79 р. |
812 357,76 р. |
| 3 |
Коленков Д.Ю. |
3,00% |
560 246,73 р. |
72 832,07 р. |
487 414,66 р. |
| 4 |
Кучеренко Ю.К. |
0,00% |
0,00 р. |
0,00 р. |
0,00 р. |
| 5 |
Меньшиков В.В. |
4,00% |
746 995,64 р. |
97 109,43 р. |
649 886,21 р. |
| 6 |
Минина Е.А. |
20,00% |
3 734 978,20 р. |
485 547,17 р. |
3 249 431,03 р. |
| 7 |
Морёнов Д.А. |
15,00% |
2 801 233,65 р. |
364 160,37 р. |
2 437 073,28 р. |
| 8 |
Парфёнов А.А. |
1,00% |
186 748,91 р. |
24 277,36 р. |
162 471,55 р. |
| 9 |
Пархоменко Е.В. |
11,00% |
2 054 238,01 р. |
267 050,94 р. |
1 787 187,07 р. |
| 10 |
Платонов А.Ю. |
4,00% |
746 995,64 р. |
97 109,43 р. |
649 886,21 р. |
| 11 |
Францев Д.Ю. |
4,00% |
746 995,64 р. |
97 109,43 р. |
649 886,21 р. |
| 12 |
Хорошилов А.С. |
1,00% |
186 748,91 р. |
24 277,36 р. |
162 471,55 р. |
| 13 |
Худов М.А. |
10,00% |
1 867 489,10 р. |
242 773,58 р. |
1 624 715,52 р. |
| Итого
|
18 674 891,00 р.
|
Задача №2.2 (общая)

Пояснения:
КТУ= 1 – Сумм (всех работников)
Начислено = КТУ * Общую сумму
НДФЛ = 0,13 * начислено
На руки = начислено – НДФЛ
Задача №3 (общая)
а)  необходимо найти значение. необходимо найти значение.
| 1 |
0,333333 |
| 2 |
0,666667 |
| 3 |
1 |
| 4 |
1,333333 |
| 5 |
1,666667 |
| 6 |
2 |
| 7 |
2,333333 |
| 8 |
2,666667 |
| 9 |
3 |
| 10 |
3,333333 |
| 11 |
3,666667 |
| 12 |
4 |
| 13 |
4,333333 |
| 14 |
4,666667 |
| 15 |
5 |
| 16 |
5,333333 |
| 17 |
5,666667 |
| 18 |
6 |
| 19 |
6,333333 |
| 20 |
6,666667 |
| 21 |
7 |
| 22 |
7,333333 |
| 23 |
7,666667 |
| 24 |
8 |
| 25 |
8,333333 |
| 0,595887 |
Пояснения:
Нахождение значения:
СУММ (выделить все значения второго столбца)^(1/3)/8;
Окончательное значение выделено черным цветом.
б) 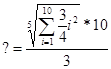 необходимо найти значение. необходимо найти значение.
| 1 |
1 |
0,75 |
| 2 |
4 |
3 |
| 3 |
9 |
6,75 |
| 4 |
16 |
12 |
| 5 |
25 |
18,75 |
| 6 |
36 |
27 |
| 7 |
49 |
36,75 |
| 8 |
64 |
48 |
| 9 |
81 |
60,75 |
| 10 |
100 |
75 |
| 10,35102 |
Пояснения:
Нахождение значения:
(((СУММ (выделяем все значения последнего столбца))^(1/5))*10)/3.
Окончательное значение выделено черным цветом.
Задача №4 (общая)
Построение графиков функции.
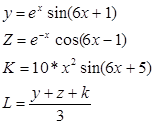 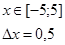
| x |
y |
z |
k |
l |
| -5 |
0,004472 |
135,7598 |
33,08794 |
56,28407 |
| -4,5 |
-0,00847 |
-86,651 |
1,79239 |
-28,289 |
| -4 |
0,015499 |
54,11784 |
-23,9804 |
10,051 |
| -3,5 |
-0,02757 |
-33,1142 |
35,26816 |
0,708811 |
| -3 |
0,047865 |
19,85866 |
-37,815 |
-5,9695 |
| -2,5 |
-0,08131 |
-11,6667 |
34,00132 |
7,417775 |
| -2 |
0,135334 |
6,705175 |
-26,2795 |
-6,47965 |
| -1,5 |
-0,22076 |
-3,76046 |
17,02806 |
4,348948 |
| -1 |
0,352769 |
2,049319 |
-8,41471 |
-2,00421 |
| -0,5 |
-0,55152 |
-1,07768 |
2,273244 |
0,214684 |
| 0 |
0,841471 |
0,540302 |
0 |
0,460591 |
| 0,5 |
-1,24776 |
-0,25241 |
2,473396 |
0,324411 |
| 1 |
1,785875 |
0,104353 |
-9,9999 |
-2,70322 |
| 1,5 |
-2,43813 |
-0,03247 |
22,28867 |
6,606022 |
| 2 |
3,104638 |
0,000599 |
-38,4559 |
-11,7836 |
| 2,5 |
-3,50738 |
0,011224 |
57,05908 |
17,85431 |
| 3 |
3,010364 |
-0,0137 |
-76,1598 |
-24,3877 |
| 3,5 |
-0,29312 |
0,012323 |
93,41341 |
31,04421 |
| 4 |
-7,22616 |
-0,00976 |
-106,181 |
-37,8058 |
| 4,5 |
24,38616 |
0,007187 |
111,6639 |
45,35242 |
| 5 |
-59,9645 |
-0,00504 |
-107,046 |
-55,6717 |
Пояснения:
Y= exp(x)*sin (6*x+1)
Z= exp (-x)*cos (6*x-1)
K = 10*x^2*sin (6*x+5)
L=срзнач (y:k)
Задача №5 (общая)
Дама сдавала в багаж:
· диван (1 шт.);
· чемодан (2 шт.);
· саквояж (2 шт.);
· корзина (5 шт.); картина (1 шт.);
· картонка (8 шт.);
· собачонка (1 шт.).
Известно, что общая стоимость перевозок багажа составляет – 22 222 руб. 22 коп.
При этом известно, что перевозка 1 дивана стоит как 0,25 дивана;
1 Саквояжа – ½ чемодана + 10 руб.
1 Корзины – ½ (ср. арифм. (чемодан, саквояж))
1 Картины – 2,5 * дивана
1 Картонка – 5% от чемодана
Собачонка – 10 * корзина
Решение:
| Расчет стоимости багажа |
| №п/п |
наименование |
количество |
цена |
Итого |
| 1 |
диван |
1 |
3 850,55 р. |
3 850,55 р. |
| 2 |
чемодан |
2 |
962,64 р. |
1 925,27 р. |
| 3 |
саквояж |
2 |
491,32 р. |
982,64 р. |
| 4 |
корзина |
5 |
363,49 р. |
1 817,44 р. |
| 5 |
картина |
1 |
9 626,37 р. |
9 626,37 р. |
| 6 |
картонка |
8 |
48,13 р. |
385,05 р. |
| 7 |
собачонка |
1 |
3 634,89 р. |
3 634,89 р. |
| Всего |
22 222,22 р. |
Задача №6 (общая)
Предприятие несет следующие расходы или издержки при производстве продукции. Постоянные издержки в месяц 1 234 567, 89 руб.
Переменные издержки на единицу продукции (себестоимость) – 252,16 руб.
Объем производимой продукции за тот же один период составляет – 819 шт.
Требуется определить цену реализации товара, чтобы мы находились в точке безубыточности (прибыль=0).
Решение:
| Постоянные издержки |
1 234 567,89 р. |
| Себестоимость на 1 изделие |
252,16 р. |
| Объем |
819 |
| Цена |
1 759,57 р. |
| Прибыль |
0,00 р. |
| 820 |
1507,408901 |
| 830 |
16581,49791 |
| 840 |
31655,58692 |
| 850 |
46729,67593 |
| 860 |
61803,76495 |
| 870 |
76877,85396 |
| 880 |
91951,94297 |
| 890 |
107026,032 |
| 900 |
122100,121 |
| 910 |
137174,21 |
| 920 |
152248,299 |
| 930 |
167322,388 |
| 940 |
182396,477 |
| 950 |
197470,566 |
| 960 |
212544,6551 |
| 970 |
227618,7441 |
| 980 |
242692,8331 |
| 990 |
257766,9221 |
| 1000 |
272841,0111 |
| 1010 |
287915,1001 |
| 1020 |
302989,1891 |
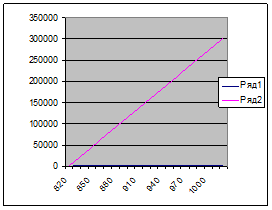
Пояснения:
Рассчитаем, какова будет прибыль, если объём продукции будет меняться в диапазоне от 820 до 1020 с шагом 10.
Прибыль = объем* (цена – себестоимость) – постоянные издержки.
|