Решить графоаналитическим методом.
Задача 1
maxj (X) = - 2x1
+ x2
+ 5x3
при 4x1
+ 2x2
+ 5x3
³ 12
6x1
- 3x2
+ 4x3
= 18
3x1
+ 3x2
- 2x3
£ 16
Х ≥ 0
Здесь число n = 3 и число m = 3.
Выразим из ограничений и х3
:
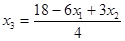 ≥ 0 ≥ 0
Подставим его в целевую функцию
maxj (X) = 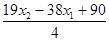
Получим новые ограничения:

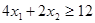
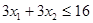
х ≥ 0
Получили задачу линейного программирования в основном виде для n = 2
Вычисляем градиент 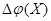 : :
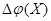 = = 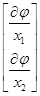 = = 
х2
=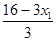 |
|
  Рисунок 1
Прямые a, c, d и eпересекаются и образуют четырехугольник ACDE. Определим max φ (Х), который удовлетворяет условию Х>=0:
Это точка D (0,7; 4,7; 0).
Функция φ (Х*
) в точке D:
φ (Х*
) = 38,3
Найти экстремумы методом множителей Лагранжа
Задача 2
extr φ (X) = 4x1
- x2
2
- 12
при x1
2
+ x2
2
= 25
Составим функцию Лагранжа:
L (X,λ) = 4x1
- x2
2
- 12 + λ (x1
2
+ x2
2
- 25)
h (X) = x1
2
+ x2
2
- 25 = 0 - функция ограничения.
Составим систему уравнений из частных производных и приравняем их нулю.
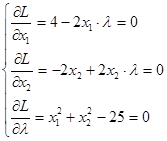
Решим данную систему уравнений:
2x2 (
λ- 1) = 0
Предположим, что x2
≠ 0, тогда λ= 1 подставим в первое уравнение системы.
4 - 2x1
= 0
2x1
= - 4
x1
= 2
Подставим x1
в третье уравнение системы.
4 +x2
2
- 25 = 0
x2
2
- 21 = 0
x2
2
= 21
x2
= ±4,5826
Параболоид вращения функции h (x).
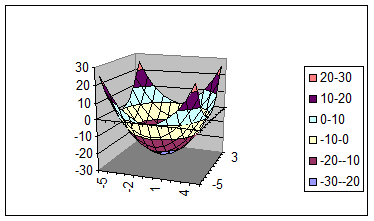
В двухмерной проекции график выглядит так:
 Рисунок 2.
На рис.2 видно, что в точках А1
и А2
функция φ (X) = h (X). В этих точках функция φ (X) равна минимальному значению.
(X*
,λ*
)
N
|
X1
*
|
X2
*
|
λ*
|
φ (X*
) |
Примечание |
| 1 |
2 |
4,5826 |
1 |
-24,25 |
Min |
| 2 |
2 |
-4,5826 |
1 |
-24,25 |
Min |
Решить обобщенным методом множителей Лагранжа или на основе условий Куна-Таккера.
Задача 3
extr φ (X) = 9 (x1
- 5) 2
+ 4 (x2
- 6) 2
= 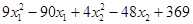
при 3x1
+ 2x2
>= 12
x1
- x2
<= 6
Решим задачу на основе условий Куна-Таккера.
Составим функцию Лагранжа.
L (X,λ) = 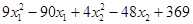 + λ1
(3x1
+ 2x2
- 12) + λ2
(x1
- x2
- 6) = + λ1
(3x1
+ 2x2
- 12) + λ2
(x1
- x2
- 6) =
Составим систему уравнений из частных производных и приравняем их нулю.
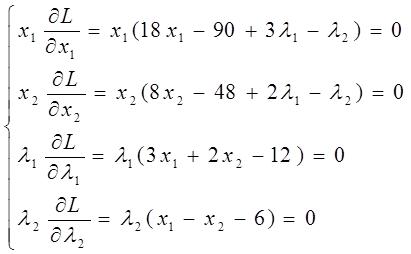
Решим систему уравнений.
1) Предположим, что λ2
≠ 0, тогда из уравнения (d) получим
x2
= х1
- 6
Пусть λ1
= 0 и x1
≠ 0, тогда из уравнения (а) получим
18x1
- 90 - λ2
= 0, λ2
= 18х1
- 90
Пусть x2
≠ 0, тогда из уравнения (b) получим
8x2
- 48 - λ2
= 0
Подставив в уравнение выражения для x2
и λ2
, получим
x1
= 4
x2
= - 2
x1
*
= 4; x2
*
= - 2; φ (Х) *
= 265
Трехмерный график целевой функции для данной задачи
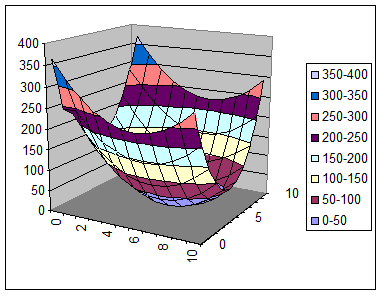
Двухмерная проекция
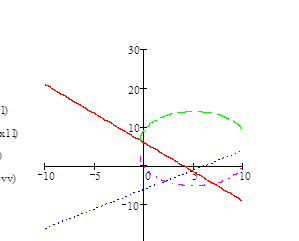 Рисунок 3
На рис.3 видно, что в точке А функция b (X) = a (X), которые находятся в параболоиде вращения целевой функции.
В этой точке функция φ (X) равна максимальному значению.
2) Предположим, что λ2
= 0 и x2
≠ 0, тогда из уравнения (b) получим
8x2 -
48 + 2λ1
= 0
x2
= 
x2
= 6 - 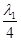
Предположим, что x1
≠ 0, тогда из уравнения (а) выразим x1
.
18х1
- 90 + 3λ1
= 0
18 = 90 - 3λ1
х1
= 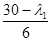
х1
= 5 - 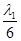
Подставим выражения для x1
и x2
в уравнение (с) системы.
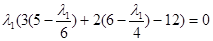
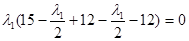
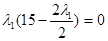
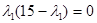
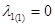 
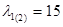
а) 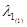 = 0, x1
= 5; x2
= 6 = 0, x1
= 5; x2
= 6
б)  = 15 = 15
x1
= 2,5; x2
= 2,25
Подставив корни x1
= 5; x2
= 6 в целевую функцию получим φ (Х) = 0, а корни x1
= 2,5; x2
= 2,25 - получим φ (Х) = 112,49
Таким образом:
x1
*
= 5; x2
*
= 6; φ*
(Х) = 0
На рис.4 видно, что в точке В функция φ (X) = a (X). В этой точке функция φ (X) равна минимальному значению.
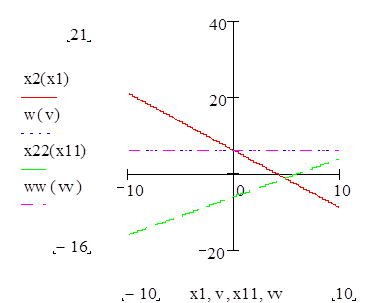 Рисунок 4
X*
N
|
X1
*
|
X2
*
|
φ (X*
) |
Примечание |
| 1 |
5 |
6 |
0 |
Min |
| 2 |
4 |
-2 |
265 |
Max |
Получить выражение вектор-функции и матрицы Якоби системы и составить алгоритм численного решения задачи на основе условий Куна-Таккера.
Задача 4
maxφ (X) = - x1
2
- x2
2
+2х2
при x1
+ x2
>= 18
x1
+ 2 x2
>= 14
Х>=0
Найдем выражение вектор-функции системы.
Составим функцию Лагранжа.
L (X,λ) = - x1
2
- x2
2
+ 2х2
+ λ1
(x1
+ x2
- 18) + λ2
(x1
+ 2x2
- 14)
Вектор-функция системы:

Составим матрицу Якоби.
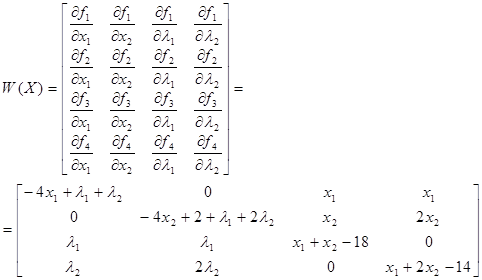
Составим алгоритм численного решения задачи:

Рисунок 5.
|