Аннотация
Данный курсовой проект посвящен рассмотрению и изучению алгоритмов нечисленной обработки данных – линейный и двоичный поиск, а также упорядочение массива методом сортировки деревом. Алгоритмы реализованы на языке Turbo Pascal 7.0.
Содержание
1 Постановка задачи. 3
2 Метод решения. 4
2.1 Сортировка двоичным деревом. 4
2.1.1 Организация массива в виде двоичного дерева. 4
2.1.2 Простейший способ. 4
2.1.3 Описание построения дерева. 5
2.1.4 Описание сортировки деревом. 6
2.2 Линейный поиск. 7
2.3 Двоичный поиск. 8
2.4 Метод оценки времени поиска. 10
3 Алгоритмизация задачи. 11
3.1 Ввод и вывод массива. 11
3.2 Линейный поиск. 12
3.3 Построение двоичного дерева. 12
3.4 Сортировка двоичным деревом. 13
3.5 Двоичный поиск. 14
3.6 Запись в файл. 15
4 Инструкции по пользованию программой. 16
4.1 Руководство пользователя. 16
4.2 Руководство программиста. 16
4.2.2 Процедура Vivod. 17
4.2.3 Процедура Save_To_File. 17
4.2.4 Процедура Lin_Poisk. 17
4.2.5 Процедура Dv_Poisk. 17
4.2.6 Процедура Tree. 18
4.2.7 Процедура Tree_Sort 18
4.3 Область и условия применения программы.. 18
5 Анализ результата. 19
5.1 Линейный поиск. 19
5.2 Двоичный поиск. 20
5.3 Анализ сортировки деревом. 22
Заключение. 24
Список литературы.. 25
Приложение А.. 26
Приложение Б. 29
1 Постановка задачи
Необходимо:
1) Создать набор входных данных длиной 16, 128, 512, 1024 элементов для программ поиска и сортировки. Для массива длиной, не превышающей 16 элементов, предусмотреть ввод элементов с клавиатуры, в остальных случаях – генератором случайных чисел.
2) Разработать алгоритм и программу упорядочения методом минимальной по памяти турнирной сортировки.
3) Разработать алгоритм и программу поиска заданного элемента в неупорядоченных массивах. Метод линейного и двоичного поиска.
4) Осуществить отладку программы на тестовых примерах.
5) Оценить время сортировки и поиска информации для массивов заданной длины.
Требования к программе:
1) основные алгоритмы оформить в виде подпрограмм;
2) программа должна быть самодокументированной;
Обеспечить формирование массива:
1) путем ввода элементов с клавиатуры при n≤16;
2) с помощью генератора случайных чисел при n>16;
2 Метод решения
2.1 Сортировка двоичным деревом
2.1.1 Организация массива в виде двоичного дерева
Чтобы облегчить поиск в массиве элемента с нужным значением признака, не обязательно упорядочивать его по этому признаку в линейную последовательность. Двоичным называется ориентированное дерево, у которого в каждую вершину, кроме одной, корня дерева, заходит одна дуга и из каждой вершины исходит не более двух дуг. Ветвью дерева называют поддерево, состоящее из некоторой дуги данного дерева, ее начальной и конечной вершин, а также всех вершин и дуг, лежащих на всех путях, выходящих из конечной вершины этой дуги.
2.1.2 Простейший способ
Сначала рассматривается весьма простой метод построения дерева, организующего массив. При этом методе, в известном смысле, отдаются на волю случая. Как будет видно, можно все же получить хорошие результаты, если в исходном состоянии массива значения признака, взятые в порядке возрастания номеров элементов, образуют хорошо перемешанную последовательность.
Первый элемент массива поместим в корень дерева. Со вторым элементом поступают так. Сравнивают значение p2 признака этого элемента со значением p1 признака элемента, помещенного в корень дерева (т.е первого элемента).
Если p2<p1, то к корню пририсовывают дугу, направленную влево, и помещают второй элемент в конце этой дуги. Если же p2≥p1, то делают то же самое, но дугу направляют вправо. В общем случае, когда требуется выбрать место на дереве для i-го элемента массива (к этому моменту дерево уже содержит i- 1 вершину и i-2 дуги), поступают следующим образом. В процессе выбора просматривается некоторый путь по дереву (цепочка смежных неповторяющихся вершин и дуг), выходящий всегда из корня. Чтобы, находясь в некоторой вершине пути, определить, обрывается ли путь в этой вершине, а если нет, то какая вершина следующая, применяется один и тот же прием для каждой вершины, в том числе и для корня. Сравнивается значение pi признака размещаемого элемента со значением pk признака элемента, помещенного в данной вершине. Если pi <pk , то смотрят, исходит ли из этой вершины дуга влево. Если исходит, то вершина в конце этой дуги будет следующей вершиной пути, если нет, то достраивают эту дугу и помещают i-й элемент в ее конце. Если же pi ≥ pk , то все происходит аналогично, но с дугой, направленной вправо. Таким образом, из каждой вершины может исходить самое большее две дуги, как и полагается для двоичного дерева.
Метод организации массива в виде двоичного дерева требует несколько больших затрат как на организацию массива, так и на поиск в нем нужного элемента, чем это минимально необходимо. Впрочем, это увеличение не столь существенно. Этот метод оптимален по порядку роста трудоемкости поиска в зависимости от размера массива. Это означает, что для данного метода, так же как и для оптимального, эта зависимость имеет вид c∙log n (с точностью до величин меньшего порядка роста) и разница заключается лишь в значении коэффициента пропорциональности c.
2.1.3 Описание построения дерева
Пусть каждый элемент исходного массива a состоит из двух полей: признака a[i,1] и собственно значения элемента a[i,2], где i – номер элемента в исходном массиве. Чтобы описать массив, упорядоченный в виде дерева, каждый элемент надо снабдить ещё, по меньшей мере двумя полями, содержащими номера элементов, расположенных в конце левой и правой дуг, исходящих из вершины, в которую помещён данный элемент. Этих двух дополнительных полей достаточно для построения дерева и для поиска в нем. Однако для других операций с деревом желательно иметь ещё одно поле, содержащее номер того элемента, к которому подвешен (безразлично, слева или справа) данный элемент. Пусть исходный массив уже содержит все необходимые поля, то есть, описан как
mas=array [1..n, 1..5] of integer,
но значения дополнительных полей a[i,3], a[i, 4] и a[i,5] перед началом работы алгоритма не определены. Называются эти поля соответственно левым, правым и обратным указателем. Если после окончания работы алгоритма левый (правый) указатель какого-либо элемента содержит нуль, это означает, что из вершины, в которую помещён данный элемент, не исходит левая (правая) дуга. Обратный указатель содержит нуль только для первого элемента, который помещён в корне дерева. Остальные детали процедуры ясны из приведённого в начале этого раздела словесного описания алгоритма.
2.1.4 Описание сортировки деревом
Имеются два массива: a – исходный и b – отсортированный. В массиве b элементы массива a расположены в порядке возрастания значения признака. Если у элемента есть левая ветвь, то элемент с наименьшим значением признака разыскивается на этой ветви. Если у элемента левой ветви нет, то он переносится в массив b, так как в массиве нет элемента с меньшим значением признака. После этого очередной элемент разыскивается в правой ветви, если она есть, или возвращается по обратному указателю. После возвращения к какому-либо элементу по левой или правой ветви дальнейшие действия идут так, как будто у этого элемента соответствующей ветви нет.
2.2 Линейный поиск
Для неупорядоченного исходного массива единственным способом нахождения заданного элемента в этом массиве является линейный поиск. Этот метод состоит в последовательном сравнении каждого элемента массива с заданным для поиска элементом. При линейном поиске иногда просматривается половина, а то и больше элементов исходного массива. Этот метод удобен и прост для массивов с меньшей длиной. Для массивов большей длины это метод вызывает затруднения, так как время поиска будет очень медленным.
Применим метод линейного поиска на примере поиска в неупорядоченном массиве A элемента X=11. Дан массив A, который состоит из 10 элементов.
Таблица 1 – Линейный поиск
| № Элемента |
Сравнение |
№ Проверки |
| 1 |
5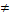 11 11 |
1 |
| 2 |
12≠11 |
2 |
| 3 |
68≠11 |
3 |
| 4 |
0≠11 |
4 |
| 5 |
92≠11 |
5 |
| 6 |
87≠11 |
6 |
| 7 |
7≠11 |
7 |
| 8 |
32≠11 |
8 |
| 9 |
11=11 |
9 |
| 10 |
24 |
Из таблицы 1 видно, что для нахождения элемента X=11 пришлось выполнить 9 сравнений. Если бы элемента 11 не оказалось под номером 9, то поиск выполнялся бы до его нахождения, либо до окончания массива.
2.3 Двоичный поиск
Одним из эффективных методов поиска в больших отсортированных массивах является двоичный, другое название бинарный, поиск. Так называемый, поиск методом деления пополам. Вместо просмотра подряд всех элементов массива делим его пополам. Так как массив отсортирован, то, сравнивая искомый элемент со значением среднего элемента массива, можно сделать вывод, о том, что может ли быть элемент с таким значением в массиве и в какой половине он находиться, то есть, определить область дальнейшего поиска. Затем делится пополам та часть массива, в которой находится элемент, и так до тех пор, пока рассматриваемая часть массива получится состоящей из одного элемента.
Допустим, есть упорядоченный по возрастанию массив из целых чисел. Необходимо определить, содержит ли этот массив некоторое число (образец).
Алгоритм двоичного поиска:
1. Сначала образец сравнивается со средним (по номеру) элементом массива
- если образец равен среднему элементу, то задача решена;
- если образец больше среднего элемента, то это значит, что искомый элемент расположен, ниже среднего элемента (между элементами с номерами sre+1), и за новое значение verhe принимается sre+i, а значение nize не меняется;
- если образец меньше среднего элемента, то это значит, что искомый элемент расположен выше среднего элемента (между элементами с номерами verhe и sre-1), и за новое значение nize принимается sre-1, а значение verhe не меняется.
2. После того как определена часть массива, в которой может находиться искомый элемент, вычисляется новое значение sredе и поиск продолжается.
Применим метод двоичного поиска на примере поиска в упорядоченном массиве. X – искомый элемент, равный 11, а A – массив, состоящий из 10 элементов:
1) 0 - verhe
5
7
11
12 - srede
24
32
68
87
92 – nize
srede равный 12>11 = X, следовательно искомый элемент находится выше среднего элемента.
2) 0 - verhe
5
7 - srede
11– nize
Srede равный 7< 11=X, значит нужный элемент находится ниже среднего элемента. Выполняем дальнейшее сравнение. Так как ниже остался всего один элемент, то сравниваем его с искомым.
3) 11=11
В итоге нужный элемент найден на третьем сравнении. Данный пример наглядно показывает всё удобство и легкость двоичного метода поиска. Результаты работы программы приведены в приложении Г.
2.4 Метод оценки времени поиска
Для сравнительной оценки быстроты поисков, введем условную единицу времени, равную времени, затраченному на сравнение двух элементов. Для теоретической оценки средней быстроты поиска используем формулы:
tлин = 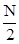 , ,
где tлин – среднее время линейного поиска; (1)
N – размер массива.
tдв = log2 N,
где tдв – среднее время двоичного поиска; (2)
N – размер массива.
3 Алгоритмизация задачи
Решение задачи, поставленной в курсовом проекте, включает в себя следующие этапы:
Формирование исходного неупорядоченного массива и запись его в текстовый файл.
Линейный поиск заданного элемента в массиве.
Построение двоичного дерева.
Сортировка исходного массива деревом.
Двоичный поиск заданного элемента в отсортированном массиве.
Запись отсортированного массива в текстовый файл.
3.1 Ввод и вывод массива
Схема алгоритма создания неупорядоченного массива приведена в приложении В. Алгоритм реализован в виде процедуры Vvod (приложение Б).
Шаг 1. Если n≤16, то переход на шаг 2, иначе шаг 4.
Шаг 2 Ввод осуществляется с клавиатуры в цикле с параметром i:
for i:=1 to n do read(A[i]).
Шаг 3. Запись каждого элемента в текстовый файл F_1 после считывания.
Шаг 4. Массив формируется с помощью датчика случайных чисел также в цикле с параметром i : for i:=1 to n do
A[i]:=random(1000);
Шаг 5. Запись сформированного массива в текстовый файл F_1, элементы которого располагаются в четырёх позициях.
Процедура Vivod выводит на экран сформированный неупорядоченный массив.
3.2 Линейный поиск
Схема алгоритма линейного поиска приведена в приложении В. Алгоритм реализован в виде процедуры Lin_Poisk (приложение Б).
Шаг 1. Установить счетчик количества сравнений в 0: k:=0.
Шаг 2. Последовательное сравнение элементов исходного массива с заданным элементом x в цикле с параметром i.
Шаг 3. Элемент массива равен искомому элементу: a[i]=x, то счетчику присваивается индекс искомого элемента: k:=i, а также осуществляется выход из цикла с помощью процедуры break;
Шаг 4. Если k≠0, тогда шаг 5, иначе шаг 6.
Шаг 5. Вывод на экран сообщения Writeln (‘Element naiden. Sravnenii-‘,k).
Шаг 6.Вывод на экран сообщения Writeln (‘Element ne naiden’).
3.3 Построение двоичного дерева
Процедура Tree представляет исходный массив A в виде дерева B. Формирование двоичного дерева выполняется следующим образом:
Шаг 1. Обнуляются поля первого элемента, содержащего левый, правый и обратный указатели b[1,3]:=0; b[1,4]:=0; b[1,5]:=0.
Шаг 2. Записываются элементы массива в получаемое дерево. В дереве b заполняются первые 2 поля – поле значения и признака. Первый элемент является корнем дерева
Шаг 3. Цикл организации двоичного дерева. Для каждого элемента массива (дерева), начиная со второго, необходимо выполнять следующие действия:
Шаг 3.1. Просмотр начинается со сравнения i-го элемента с корнем дерева, т.е. индекс k устанавливается в единицу k:=1.
Шаг 3.2. Сравнение: если i-й элемент массива меньше корня дерева, тогда его необходимо записать в левую ветвь j:=3, иначе – в правую ветвь j:=4.
Шаг 3.3. Проверка: если у k-го элемента есть левый или правый потомок, то переход на Шаг 3.4, иначе – переход на Шаг 3.5.
Шаг 3.4. За индекс k необходимо взять значение переменной s, которое содержит указатель правого или левого потомка k-го элемента и переход на Шаг 3.2.
Шаг 3.5. В поле указателя левого или правого потомка k-го элемента записывается значение индекса i. Поля i-го элемента, содержащие указатели левого, правого потомков и предка, обнуляются.
Данный алгоритм реализован в виде процедуры Tree (Приложение Б). Схема алгоритма процедуры Tree представлена в Приложении В.
3.4 Сортировка двоичным деревом
Идея сортировки деревом заключается в следующем. Если у элемента есть левая ветвь, то элемент с наименьшим значением признака надо искать на этой ветви. Если у элемента левой ветви нет, то он должен быть перенесён в результирующий массив b1. После этого очередной элемент разыскивается в правой ветви, если она есть, или возвращается по обратному указателю. После возвращения к какому-либо элементу по левой или правой ветви дальнейшие действия идут так, как будто у этого элемента соответствующей ветви нет. И так до тех пор, пока все элементы исходного массива, образующие двоичное дерево, не будут упорядочены по возрастанию.
Алгоритм сортировки деревом приведен ниже:
Шаг 1. Записываются элементы исходного массива (дерева) в результирующий массив (сортируемое дерево). Просмотр дерева начинается с первого элемента i:=1. Устанавливается счетчик, индекс для просмотра сортируемого дерева k:=0.
Шаг 2. Проверяется i-й элемент массива (дерева) на наличие левого потомка. Если он имеется, то за i-й элемент берется левый потомок и повторяется Шаг 2. Увеличивается счетчик количества перестановок m:=m+1.
Шаг 3. Увеличение счетчика k, в сортируемом массиве берется следующий элемент k:=k+1 и вместо него записывается i-й элемент.
Проверяется i-й элемент массива (дерева) на наличие правого потомка. Если он имеется, то за i-й элемент берется правый потомок и повторяется Шаг 2. Увеличивается счетчик количества перестановок m:=m+1.
Шаг 4. Индексу j присваивается значение индекса i j:=i, за индекс i берется обратный указатель (предок) i:=b[i,5], и если предок существует, то происходит следующая проверка: если предок (i-й элемент) больше своего потомка (j-й элемент), то повторить Шаг 3, иначе повторить Шаг 4.
Шаг 5. Увеличение счетчика перестановок m:=m+1.
Шаг 6. Запись отсортированного массива (дерева) в файл.
3.5 Двоичный поиск
Схема алгоритма двоичного поиска приведена в приложении В. Алгоритм реализован в виде процедуры Dv_Poisk (приложение Б).
Шаг 1. Установить начальные значения верхнего и нижнего индекса, счетчика сравнений k и : vi:=N, ni:=1, k:=0 и f:=false,так как элемент ещё не найден.
Шаг 2. Нахождение среднего элемента массива: sri:=((ni+vi) div 2).
Шаг 3. Увеличение счетчика k на единицу: k:=k+1;
Шаг 4. Если средний элемент равен искомому: a[sri]=x, то элемент найден: f:=true;
Шаг 5. Если x>a[sri] переход на шаг 6, иначе на шаг 7.
Шаг 6. За новое значение ni принимается sri+1, а значение vi не меняется.
Шаг 7. За новое значение vi принимается sri-1, а значение ni не меняется.
Шаг 8. Повторение цикла до тех пор, пока счетчик не станет больше максимального количества сравнений: k>log2n , либо элемент не будет найден.
Шаг 9. Если f:=true, то выполняется шаг 10, иначе шаг 11.
Шаг 10. На экран выводится: (‘Element naiden, Index=’, sri,'. Sravnenii ‘,k).
Шаг 11.На экран выводится: (‘Element ne naiden’).
3.6 Запись в файл
Схема алгоритма записи в файл упорядоченного массива приведена в приложении В. Алгоритм реализован в виде процедуры Save_To_File (приложение Б).
Шаг 1. При n≤16 массив записывается в файл после каждой перестановки.
Шаг 2. При n≥128 массив записывается в файл через каждые 10 перестановок.
Каждый элемент отсортированного массива располагается в четырёх позициях.
4 Инструкции по пользованию программой
4.1 Руководство пользователя
Программа, реализованная в соответствии с задачей, поставленной на курсовом проекте, написана на языке Turbo Pascal 7.0. Для запуска программы необходимо иметь компилятор Turbo Pascal 7.0. После запуска программы следует нажать комбинацию клавиш Ctrl+F9. В появившемся окне будет сообщение с просьбой ввести число элементов. Введите целое число n от 16 до 1024 элементов (можно и меньше 16), а затем нажмите клавишу Enter. Если введено n≤16, то ввод элементов надо осуществить с клавиатуры, то есть вручную. Каждый вводимый элемент должен быть положительным и меньше 1000.
Если введено n>16, то программа сформирует массив самостоятельно при помощи датчика случайных чисел;
Дальше потребуется ввести элемент для поиска - x. Затем нажать Enter.
В дальнейшем программа автоматически выведет результаты поисков: линейного и двоичного. Результат включает в себя:
- для линейного поиска - количество сравнений;
- отсортированный массив, где все элементы расположены по возрастанию значений;
- для двоичного поиска – количество сравнений и перестановок, а также индекс искомого элемента;
Все результаты приведены в приложении Г.
4.2 Руководство программиста
Программа, представленная в данном курсовом проекте, разработана на языке высокого уровня – Turbo Pascal 7.0. Она состоит из основной программы и 7 подпрограмм (процедур).
Описания процедур приведены ниже.
4.2.1 Процедура VVod
Предназначена для формирования массива длиной до 1024 элементов. Процедура использует локальную переменную i для обращения к элементам массива. Входные параметры (в скобках указан способ передачи): n – длина массива (по значению), A – формируемый массив (по ссылке).
4.2.2 Процедура Vivod
Данная процедура выводит на экран сформированный массив, используя те же входные параметры, что и процедура VVod.
4.2.3 Процедура Save_To_File
Предназначена для записи во внешний текстовый файл сортируемый массив после заданного числа перестановок. Входные параметры: текстовый файл F(по ссылке), n – длина массива, a – записываемый сортируемый массив, m – количество перестановок.
4.2.4 Процедура Lin_Poisk
Эта процедура предназначена для поиска заданного элемента методом линейного поиска. Входные параметры: n – длина массива, a – исходный массив, x – заданный элемент. Локальные переменные: i – индекс элемента, счетчик, k – количество сравнений.
4.2.5 Процедура Dv_Poisk
Данная процедура реализует двоичный поиск. Входные параметры – те же, что и в процедуре Lin_Poisk. Локальные переменные: k – количество сравнений, ni – индекс нижней границы массива, vi – индекс верхней границы массива, sri – индекс среднего элемента массива.
4.2.6 Процедура Tree
Для построения дерева из исходного массива используется процедура Tree. Она формирует дерево b из массива a. Входные параметры: a - исходный массив (по значению), n – длина массива (по значению). Выходной параметр: b – двумерный массив (дерево). Локальные переменные: i,j – индексы элемента в дереве.
4.2.7 Процедура Tree_Sort
Сортирует дерево, полученное из исходного массива. Входные параметры: b – исходное дерево (по значению), n – длина массива (по значению). Выходной параметр: b1 – результирующий массив (отсортированное дерево). Локальные переменные: k – количество узлов в дереве, m – количество перестановок, i1 – индекс элемента в дереве (массиве).
4.3 Область и условия применения программы
В данной программе были разработаны алгоритмы нечисленной обработки данных – линейный и двоичный поиск, сортировка деревом. Сортировку деревом очень удобно использовать, когда необходимо сэкономить максимально возможно количество времени, но для представления дерева требуются большие затраты дополнительной памяти.
Программа является познавательной, её целесообразно использовать в качестве обучающего примера.
5 Анализ результата
На основе проведенных тестов программы был проведен анализ алгоритмов нечисленной обработки данных на примере массива длиной в 16, 128, 512, 1024 элементов.
5.1 Линейный поиск
Для проведения анализа линейного поиска в качестве заданного элемента были взяты числа, расположенные в начале, в середине, в конце и в произвольной позиции массива. Для линейного поиска теоретическое время поиска определяется по формуле Tтеор.=[время сравнения]×N/2
Результаты приведены в нижеследующей таблице.
Таблица 2. Результаты линейного поиска
| Количество элементов массива |
16 |
128 |
512 |
1024 |
| Позиция элемента |
Искомый элемент |
Количество сравнений |
Искомый элемент |
Количество сравнений |
Искомый элемент |
Количество сравнений |
Искомый элемент |
Количество сравнений |
| Первая |
5 |
1 |
0 |
1 |
48 |
1 |
0 |
1 |
| Средняя |
15 |
8 |
85 |
64 |
894 |
256 |
465 |
512 |
| Последняя |
3 |
16 |
314 |
128 |
191 |
512 |
242 |
1024 |
| Произвольная |
4 |
13 |
272 |
5 |
747 |
511 |
425 |
10 |
| Элемент отсутствует |
101 |
16 |
999 |
128 |
982 |
512 |
987 |
1024 |
| Среднее значение |
10,8 |
65,2 |
358,4 |
513,6 |
| Теоретическое значение |
8 |
64 |
256 |
512 |
По данным таблицы 2 построены графики функции зависимости времени поиска от количества элементов массива (рисунок 2).
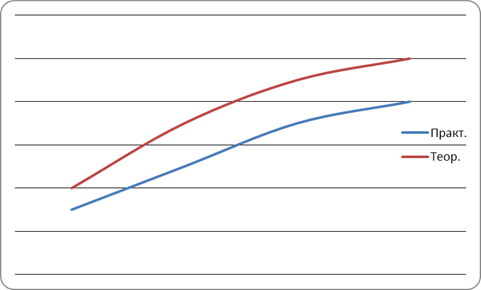
Рисунок 1. График результатов линейного поиска
Вывод: Из рисунка 2 видно, что график линейного поиска имеет линейный характер. Теоретическое время незначительно отличается от практического, что означает правильность результатов выполнения линейного поиска.
Данный метод удобен для массивов с малой длиной, но использование его для больших массивов занимает много времени.
5.2 Двоичный поиск
Анализ двоичного поиска был проведен на примере числового одномерного массива длиной в 16, 128, 512, 1024 элементов. В качестве искомых элементов были взяты числа, расположенные в первой, средней, последней и произвольной позициях. Для двоичного поиска теоретическое время поиска определяется по формуле Tтеор.=[время сравнения]× log2N
Результаты приведены в таблице, которая приведена ниже.
Таблица 3. Результаты двоичного поиска
| Количество элементов массива |
16 |
128 |
512 |
1024 |
| Позиция элемента |
Искомый элемент |
Количество сравнений |
Искомый элемент |
Количество сравнений |
Искомый элемент |
Количество сравнений |
Искомый элемент |
Количество сравнений |
| Первая |
0 |
4 |
0 |
7 |
0 |
9 |
0 |
10 |
| Средняя |
13 |
1 |
310 |
1 |
156 |
1 |
491 |
1 |
| Последняя |
45 |
4 |
901 |
7 |
491 |
9 |
942 |
10 |
| Произвольная |
2 |
2 |
80 |
3 |
127 |
7 |
660 |
9 |
| Элемент отсутствует |
88 |
4 |
1001 |
7 |
1002 |
9 |
1003 |
10 |
| Среднее количество сравнений |
3 |
5 |
7 |
8 |
| Теоретическое значение |
4 |
7 |
9 |
10 |
Ниже приведен график зависимости времени поиска от количества элементов массива.
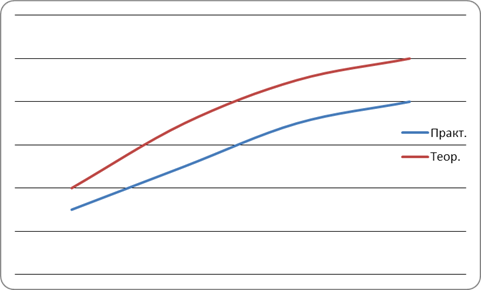
Рисунок 2. График результатов двоичного поиска
Вывод: Из рисунка 2 видно, что график двоичного поиска имеет логарифмический характер. Теоретическое время незначительно отличается от практического, что означает правильность результатов выполнения двоичного поиска.
Данный метод удобен для массивов с большой длиной, но его использование возможно только в упорядоченных массивах.
5.3 Анализ сортировки деревом
Анализ сортировки деревом был проведен на примере массива длиной в 16, 128, 512, 1024 элементов.
Результаты представлены в виде нижеследующей таблицы.
Таблица 6. Результаты сортировки
| Количество элементов в массиве |
16 |
128 |
512 |
1024 |
| Количество перестановок |
18 |
130 |
514 |
1026 |
Ниже приведен график сортировки деревом.
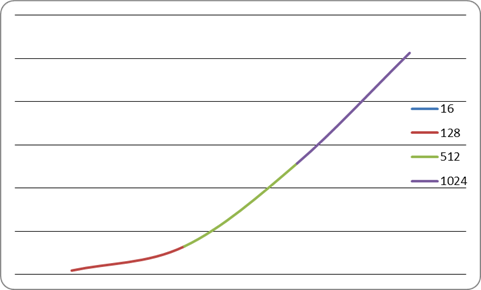
Рисунок 3. График сортировки деревом.
Вывод: Организация массива в виде двоичного дерева требует несколько больших затрат как на организацию массива, так и на поиск в нем нужного элемента, чем это минимально необходимо. Впрочем, это увеличение не столь существенно. Этот метод оптимален по порядку роста трудоемкости поиска в зависимости от размера массива.
Сортировка деревом не является минимальной по памяти, так как на построения дерева необходимы большие затраты памяти, но процесс сортировки с помощью данного метода занимает мало времени.
Заключение
В процессе выполнения данного курсового проекта изучены и разработаны алгоритмы нечисленной обработки данных: линейный и двоичный поиск заданного элемента, а также упорядочение массива методом сортировки дерева. Был проведен анализ результатов программы, который подтвердил правильность составления и отладки программы. Для наглядности результатов работы программы построены графики и составлены таблицы.
Список литературы
1. Лорин Г. Сортировка и системы сортировки. М.: Наука, 1983г.
2. Лавров С.С, Гончаров Л.И. Автоматическая обработка данных. Хранение информации в памяти ЭВМ. М.: Наука, 1971г.
3. Попов В.Б. Turbo Pascal. М.: Финансы и статистика, 2007г.
Приложение А
Таблицы идентификаторов
Таблица А.1: Идентификаторы основной программы
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| n |
Длина исходного массива до 1024 элементов |
integer |
| i |
Счетчик, индекс элемента массива |
integer |
| j |
Счетчик, индекс элемента массива, указатель |
integer |
| x |
Искомое число |
integer |
| a |
Одномерный числовой массив (исходный массив) |
mas=array [1..1024] of integer |
| b |
Двумерный числовой массив, дерево, образованное из исходного массива |
mas2=array [1..1024, 1..5] of integer |
| b1 |
Двумерный числовой массив, сортируемое дерево |
mas2=array [1..1024, 1..5] of integer |
| F |
Текстовый файл для хранения исходного массива |
text |
| F_1 |
Текстовый файл для хранения отсортированного массива, сортируемого массива после каждой перестановки |
text |
Таблица А.2: Идентификаторы процедуры VVod
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| i |
Счетчик, индекс элемента формируемого массива |
integer |
| n |
Длина формируемого массива |
integer |
| a |
Формируемый массив |
mas=array [1..1024] of integer |
Таблица А.3: Идентификаторы процедуры Vivod
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| i |
Счетчик, индекс элемента выводимого на экран массива |
integer |
| n |
Длин массива, выводимого на экран |
integer |
| a |
Выводимый на экран массив |
mas=array [1..1024] of integer |
Таблица А.4: Идентификаторы процедуры Save_To_File
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| i1 |
Счетчик, индекс элемента массива, сохраняемого в файл |
integer |
| F |
Файл, в который необходимо записывать сортируемый массив после каждой перестановки |
text |
| n |
Длина массива |
integer |
| a |
Исходный массив, сохраняемый в файл |
mas=array [1..1024] of integer |
| m |
Количество перестановок |
integer |
А.5 Идентификаторы процедуры Lin_Poisk
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| i |
Счетчик, индекс элемента массива |
integer |
| k |
Количество сравнений |
integer |
| n |
Длина массива |
integer |
| a |
Массив, в котором необходимо найти искомый элемент |
mas=array [1..1024] of integer |
| x |
Искомый элемент |
integer |
Таблица А.6 Идентификаторы процедуры Dv_Poisk
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| sri |
Индекс среднего элемента в массиве |
integer |
| k |
Количество сравнений |
integer |
| vi |
Индекс верхнего элемента в массиве |
integer |
| ni |
Индекс нижнего элемента в массиве |
integer |
| n |
Длина массива |
integer |
| a |
Массив, в котором необходимо найти искомый элемент |
mas=array [1..1024] of integer |
| x |
Искомый элемент |
integer |
| f |
Флаг нахождения искомого элемента в массиве |
boolean |
Таблица А.7: Идентификаторы процедуры Tree
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| i |
Счетчик, индекс элемента массива (строка) |
integer |
| j |
Счетчик, индекс элемента массива (столбец) |
integer |
| s |
Рабочая память, необходимая для хранения значения |
integer |
| k |
Индекс элемента в массиве |
integer |
| a |
Исходный массив, из которого следует построить дерево |
mas=array [1..1024] of integer |
| n |
Длина массива |
integer |
| b |
Дерево, полученное из массива A |
mas2=array [1..1024, 1..5] of integer |
Таблица А.8: Идентификаторы процедуры TreeSort
| Имя параметра |
Физический смысл параметра |
Тип параметра |
| k |
Число вершин дерева |
integer |
| m |
Количество перестановок |
integer |
| i1 |
Счетчик, индекс элемента массива |
integer |
| b |
Дерево, полученное из массива |
mas2=array [1..1024, 1..5] of integer |
| b1 |
Сортируемое дерево |
mas2=array [1..1024, 1..5] of integer |
| a |
Отсортированный массив |
mas=array [1..1024] of integer |
Приложение Б
Текст программы
Program Fariza_Kurs;
uses crt;
type
mas= array [1..1024] of integer;
mas2= array [1..1024, 1..5] of integer;
var n,i,j,x: integer;
a: mas;
b,b1: mas2;
f, f1: text;
Procedure Vvod(n: integer; Var a: mas);
var i: integer;
begin
if n<=16 then
begin
writeln('Vvedite elementy massiva');
for i:=1 to n do read(A[i]);
end
else
for i:=1 to n do
A[i]:=random(1000);
writeln(f,'Ishodnii masssiv');
for i:=1 to n do write(f,a[i]:4);
end;
Procedure Vivod(n: integer; a: mas);
var i: integer;
begin
for i:=1 to n do write(a[i], ' ');
end;
{zapis v fail}
Procedure Save_To_File(var f:text; n: integer; a: mas; m:integer);
var i1: integer;
begin
if n<=16 then
begin
writeln(f,m,'-yi shag:');
for i1:=1 to n do
write(f,A[i1]:4);
writeln(f);
end;
if (n>16) and (m mod 10=0) then
begin
writeln(f,m,'-yi shag:');
for i1:=1 to n do
write(f,A[i1]:4);
writeln(f);
end;
end;
{metod lineinogo poiska}
Procedure Lin_Poisk(n: integer; a: mas; x: integer);
var i,k: integer;
begin
writeln('Metod lineinogo poiska:');
k:=0;
for i:=1 to n do
if a[i]=x then begin k:=i; break;
end;
if k<>0 then Writeln('Element naiden. Sravnenii - ',k)
else writeln('Element ne naiden');
end;
{========metod dvoichnogo poiska ================}
procedure Dv_Poisk(n:integer;a:mas; x:integer);
var k,ni,vi, sri:integer;
f:boolean;
begin
writeln('Metod dvoichnogo poiska:');
vi:=N;
ni:=1;
k:=0;
f:=FALSE;
repeat
sri:=( (ni+vi) div 2);
k:=k+1;
if a[sri] = X then f:=TRUE
else if X > a[sri] then ni:=sri else vi:=sri;
until (k>trunc(ln(n)/ln(2))) or (f=true);
if f=true then writeln('Element naiden, Index=', sri,'. Sravnenii ',k)
else writeln('Element ne naiden');
end;
{predstavlenie massiva A v vide dereva}
Procedure Tree(a:mas; n: integer; var b: mas2 );
label l;
var i,j,s,k: integer;
begin
b[1,3]:=0;
b[1,4]:=0;
b[1,5]:=0;
for i:=1 to n do begin
b[i,1]:=a[i];
b[i,2]:=a[i];
end;
for i:=2 to n do
begin
k:=1;
l: if b[i,1]<b[k,1] then j:=3 else j:=4;
s:=b[k,j];
if s<>0 then begin
k:=s;
goto l;
end;
b[k,j]:=i;
b[i,3]:=0;
b[i,4]:=0;
b[i,5]:=k;
end;
end;
{sortirovka derevom}
procedure Tree_Sort(b: mas2; var b1: mas2; n: integer);
label l1,l2,l3;
var k,m,i1: integer;
begin m:=0;
for i:=1 to n do
for j:=1 to 5 do
b1[i,j]:=b[i,j];
i:=1;
k:=0;
l1:
if b[i,3]<>0 then
begin
i:= b[i,3];
goto ll;
end;
m:=m+1;
for i1:=1 to n do A[i1]:=b1[i1,1];
savetofile(f1,n,a,m);
l2:
k:=k+1;
b1[k,1]:=b[i,1];
b1[k,2]:=b[i,2];
if b[i,4]<>0 then
begin
i:=b[i,4];
goto ll;
end;
m:=m+1;
for i1:=1 to n do A[i1]:=b1[i1,1];
savetofile(f1,n,a,m);
l3:
j:=i;
i:=b[i,5];
if i<>0 then
begin
if b[i,1]> b[j,1] then goto lm else goto ln;
end;
m:=m+1;
for i1:=1 to n do A[i1]:=b1[i1,1];
savetofile(f1,n,a,m);
writeln('Otsortirovanii massiv');
Vivod(n,a);
readln;
writeln('Kolichestvo perestanovok=',m);
end;
BEGIN
writeln(' VVedite 4islo elementov massiva N<=1024');
readln(n);
assign (f, 'd:\dan.txt');
rewrite(f);
Vvod(n,a);
close(f);
writeln('Ishodnii massiv:');
Vivod(n,a);
{====================lineinii poisk===============}
writeln;
writeln('Vvedite element dla poiska');
readln(x);
LinPoisk(n,a,x);
{========sortirovka============}
assign (f1, 'd:\res.txt');
rewrite(f1);
tree(a,n,b);
Treesort(b,b1,n);
writeln(f1, 'Otsortirovannyi massiv:');
for i:=1 to n do write(f1, A[i]:4);
close(f1);
{========dvoichnii poisk===========}
DvPoisk(n,a,x);
end.
|