Идентификация параметров электромеханической системы
Введение
Цель работы: приобрести навыки определения постоянных времени системы по переходной характеристике.
Дано:
-передаточную функцию электромеханической системы:
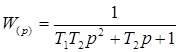 ;(1) ;(1)
-постоянные времени Т1=1, Т2=10;
-уравнения изменения скорости двигателя постоянного тока W(
t
)
:
 ;(2) ;(2)
где  - относительное время процесса; - относительное время процесса;
 - коэффициент, который характеризует степень расхождения постоянных времени Т1 и Т2; - коэффициент, который характеризует степень расхождения постоянных времени Т1 и Т2;
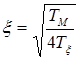 - коэффициент демпфирования; - коэффициент демпфирования;
Тм, Тя - электромеханическая и электромагнитная постоянные времени двигателя соответственно, причем Тм=Т2 в уравнении (1).
Ход работы
1. Соответственно заданных данных и передаточной функции системы строим функциональную схему системы, используя среду Matlab. Схема представлена на рисунке 1.

Рисунок 1 - Функциональная схема.
2. График переходного процесса представленный на рисунке 2.

Рисунок 2 - График переходного процесса.
По графику переходной функции (рисунок 2) определим время t1 при 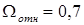 получили t1=11.95. получили t1=11.95.
Вычисляем ТМ с помощью формулы
 , ,
получили ТМ
=
9,9185
,  . .
3. При  , необходимо определить из графика , необходимо определить из графика  и решить уравнение (2) относительно h, а потом определить и решить уравнение (2) относительно h, а потом определить 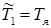 . Получили значение . Получили значение 
4. Рассчитываем значение Тя

5. Определим ошибки идентификации за формулами:
 и и 
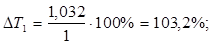 
Выводы: в ходе работы было определено постоянные времени по переходной характеристике, установлен что коэффициент, который характеризует различие постоянных времени не влияет на относительное время при разгоне двигателя к заданному единичному уровню, экспериментально получении значения постоянных времени почти совпадают с заданными.
Моделирование нелинейных объектов
Цель работы: Приобрести навыки моделирования нелинейных объектов. А также анализа их влияния на точность системы
Исходные данные:
тип двигателя: ПБВ 132;
номинальный момент: 35 Н·м;
номинальная скорость: 600 об/мин;
номинальная мощность: 2,2 кВт;
номинальное напряжение: 53 В;
номинальный ток: 50 А;
максимальный момент: 350 Н·м;
максимальная скорость: 2000 об/мин;
момент инерции якоря: 0,188/0,1901 кг/м2
;
максимальное теоретическое ускорение: 1860 м/с2
;
электромеханическая постоянная времени: 14,2 мс;
электромагнитная постоянная времени: 7,35 мс.
величина люфта: 2b=0.004.
Теоретические сведения
Люфт в кинематических передачах приводов подач станков может вызывать потерю устойчивости системы управления и ухудшение динамических показателей. Кроме этого он вызывает искажение траектории контурного движения и снижает точность обработки.
Структура механизма с нелинейностью типа «люфт» содержит нелинейный элемент, геометрическая модель которого описывается соотношениями:
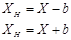 при при  , ,
где Х – входная величина нелинейного звена; ХН
– выходная величина нелинейного звена; 2b – величина люфта.
Ход работы:
С применением пакета Matlab составляем модель электромеханической системы, схема которой представлена на рисунке 1.

Рисунок 1 – Схема электромеханической системы в среде Matlab
Расчёты всех коэффициентов используемых в электромеханической системе, произведенные при помощи пакета MathCAD, приведены ниже.
Активное сопротивление якоря:

Конструктивный коэффициент:
 . .
Определяем параметры входных воздействий:
Амплитуда входного воздействия 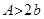 , пусть , пусть
А=1;
Частота входного воздействия
 , ,
принимаем
 . .
Входное воздействие будет иметь вид:
 . .
Эпюры сигналов на входе и выходе звена модели с нелинейным элементом типа «люфт», полученные при помощи пакета Matlab, изображены на рисунке 2.
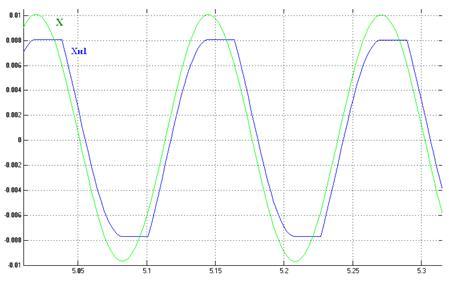
Рисунок 2 – Графики сигналов на входе и выходе звена типа «люфт» в среде Matlab
При моделировании систем с нелинейностями типа «люфт» нелинейное звено заменяется эквивалентным звеном с передаточной функцией
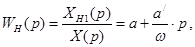
которая называется гармонической передаточной функцией нелинейного звена.
Коэффициент передачи нелинейного звена и фазовая характеристика определяются выражениями:
  . .
Коэффициенты гармонической линеаризации в функции  , характеризующие соотношения амплитуд синфазной , характеризующие соотношения амплитуд синфазной  и квадратурной и квадратурной  составляющих первой гармоники выходного сигнала ХН1
к амплитуде А
сигнала на входе Х: составляющих первой гармоники выходного сигнала ХН1
к амплитуде А
сигнала на входе Х:


Тогда передаточная функция примет вид:
 . .
Модель замены люфта линейным элементом в среде Matlab изображена на рисунке 3.
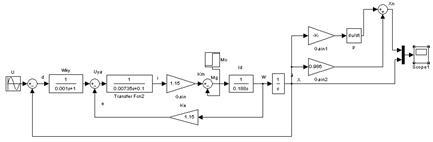
Рисунок 3 – Схема модели замены люфта линейным элементом
Полученные эпюры сигналов на входе в линейное замещённое звено типа «люфт» и на его выходе изображены на рисунке 4.
 Рисунок 4 – Графики сигналов на входе в линейное замещённое звено типа «люфт» и на его выходе
Составим модель компенсации люфта и проведём её исследование, схема модели в среде Matlab изображена на рисунке 5.
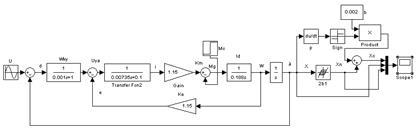
Рисунок 5 – Схема модели компенсации люфта в среде Matlab
Полученные эпюры сигналов на входе (выходе) звена типа «люфт» и после компенсации изображены на рисунке 6.
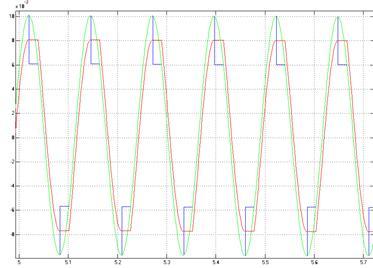 Рисунок 6 – Графики сигналов на входе звена типа «люфт» и после компенсации в среде Matlab
Выводы: в ходелабораторной работы я приобрел навыки моделирования нелинейного объекта типа «люфт», проанализировала их влияние на точность системы, составила и исследовала модель для компенсации люфта.
Оптимизация параметров пид-регуляторов для объектов управления с нелинейностями
Цель работы: освоение пакета прикладных программ NonlinearControlDesign (NCD) Blockset системы MATLAB для автоматической настройки параметров моделируемых систем электроприводов в условиях ограничений.
Индивидуальное задание:
Коэффициенты передаточной функции:
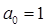 , , 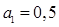 , ,  , ,  . .
Неопределенный параметр 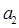 в диапазоне 0,2…0,5. в диапазоне 0,2…0,5.
Желаемые параметры качества переходного процесса δ=±5%; σ=1,2; tпп
=1,5 с
Ход работы
Передаточная функция объекта (электропривода):
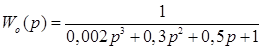
Коэффициент интегральной составляющей:
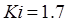 . .
Коэффициент дифференциальной составляющих:
 . .
Пропорциональная составляющая (предельное значение):
 . .
Строим исследуемую схему в среде MatLab.

Рисунок 1 – Структурная схема модели для оптимизации ПИД-регулятора
Графики переходного процесса с оптимизированными параметрами ПИД-регулятора, представлены на рисунках 3-4.

Рисунок 3 – График переходного процесса для заданной модели (Scope)
Параметры системы при оптимизации:
Starttime: 0 Stoptime: 60.
There are 2405 constraints to be met in each simulation.
There are 3 tunable variables.
There are 1 simulations per cost function call.
Creating a temporary SL model tp484964 for computing gradients...
Creating simulink model tp484964 for gradients...Done
f-COUNT MAX{g} STEP Procedures
7 -0.01 1
14 -0.01 1 Hessian modified twice
15 -0.01 1 Hessian modified twice
Optimization Converged Successfully
Active Constraints:
1203

Рисунок 4 – График переходного процесса для заданной модели (NCDOutPort)
Вывод: в ходе лабораторной работы я изучил пакет прикладных программ NonlinearControlDesign (NCD) Blockset системы MATLAB для автоматической настройки параметров моделируемых систем электроприводов в условиях ограничений, научился решать задачи оптимизации при наличии ограничений какого-либо коэффициента системы.
|