ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
по дисциплине «Теория автоматического управления»
на тему: «Исследование линейных и нелинейных систем управления».
Реферат
32 с., 26 рис., 3 табл., 3 источника информации
СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ, АВТОМАТИЧЕСКИЙ РЕГУЛЯТОР, СИНТЕЗ, УПРАВЛЯЕМОСТЬ, НАБЛЮДАЕМОСТЬ, НЕЛИНЕЙНЫЙ, АВТОКОЛЕБАНИЯ
Основной задачей курсового проекта является практическое использование знаний, полученных в процессе изучения курса, развитие навыков в расчете и выборе оптимальных параметров настройки регуляторов одноконтурных систем регулирования при проектировании.
В данной работе синтезированы П-, ПИ-, ПИД-регуляторы для линейной САР, произведены анализ качества регулирования, оценка управляемости и наблюдаемости САР, для нелинейной САР определена возможность возникновения автоколебаний.
Содержание
Введение
1 Расчет параметров настройки типовых регуляторов линейной САР
1.1 Анализ объекта регулирования
1.2 Расчет коэффициентов передачи п-регулятора
1.3 Расчет параметров настройки пи-регулятора
1.4 Расчет параметров настройки пид-регулятора
2 Анализ переходных характеристик линейной сар
2.1 Оценка качества САР по каналу управляющего воздействия
2.2 Оценка качества САР по каналу возмущающего воздействия
2.3 Оценка запаса устойчивости САР
3 Оценка управляемости и наблюдаемости линейной САР
3.1 Анализ САР с п-регулятором
3.1.1 Разработка математической модели типа «вход-состояние-выход»
3.1.2 Структурная схема САР с п-регулятором
3.1.3 Оценка управляемости САР с п-регулятором
3.1.4 Оценка наблюдаемости САР с п-регулятором
3.2 Анализ САР с пи-регулятором
3.2.1 Разработка математической модели типа «вход-состояние-выход»
3.2.2 Структурная схема САР с пи-регулятором
3.2.3 Оценка управляемости САР с пи-регулятором
3.2.4 Оценка наблюдаемости САР с пи-регулятором
3.3 Анализ САР с пид-регулятором
3.3.1 Разработка математической модели типа «вход-состояние-выход»
3.3.2 Структурная схема САР с пид-регулятором
3.3.3 Оценка управляемости САР с пид-регулятором
3.3.4 Оценка наблюдаемости САР с пид-регулятором
4 Анализ нелинейной САР
4.1 Описание нелинейной САР
4.2 Оценка возможности возникновения автоколебаний
4.3 Моделирование нелинейной САР в simulink
Заключение
Список использованных источников
Введение
Всякая система регулирования может быть представлена рядом элементов, выполняющих определенные функции. В данной курсовой работе будут рассмотрены непрерывная система регулирования, состоящая из объекта регулирования, автоматического регулятора, и нелинейная система, включающая нелинейное звено.
Принципиально отличает объект регулирования от всех остальных элементов системы то, что он обычно бывает, задан и при разработке системы автоматического регулирования не может быть изменен, тогда как остальные элементы выбираются специально для решения заданной задачи управления.
Задача выбора параметров настройки в системе автоматического регулирования или управления состоит в том, чтобы найти такие параметры регулятора, при которых переходный процесс в системе удовлетворяет следующим требованиям:
· затухание переходного процесса должно быть интенсивным;
· перерегулирование должно быть минимальным;
· продолжительность переходного процесса должна быть минимальным.
Большинство уравнений объектов являются нелинейными, однако в этих случаях знание решений, полученных для линейных систем, часто дает возможность подойти к решению для нелинейной системы.
Кривая разгона показывает реакцию объекта регулирования на единичное ступенчатое воздействие. Она строится по данным, полученным в результате решения дифференциального уравнения системы при скачкообразном входном воздействии и нулевых начальных условиях.
Передаточная функция объекта регулирования
 |
( |
Построим кривую разгона, с помощью системы MATLAB.
Script 1:
>> Wop=tf([0.9 7 2.2],[336 146 21 1]);
>> step(Wop);grid
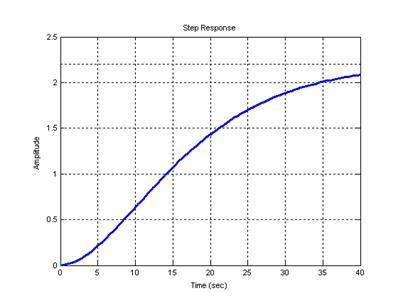
Рисунок 2 – Кривая разгона ОР
Анализируя разгонную характеристику, можно сделать вывод, что ОР обладает свойством самовыравнивания и запаздывания, является многоемкостным.
Степень колебательности переходного процесса:
Передаточная функция П-регулятора определяется по формуле
Для того чтоб определить коэффициент передачи  , необходимо построить кривую равной степени затухания.
Script 2:
>> m=0.313;
>> w=0:0.001:0.26;
>> Wex=(0.9*((j-m).*w).^2+7*(j-m).*w+2.2)./ ...
(336*((j-m).*w).^3+146*((j-m).*w).^2+21*(j-m).*w+1);
>> Win=1./Wex;
>> R=real(Win);
>> I=imag(Win);
>> Ki=w*(m^2+1).*I;
>> Kp=m.*I-R;
>> plot(Kp,Ki);xlabel('Axis Kp');ylabel('Axis Ki');grid
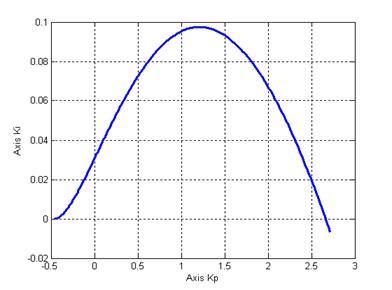
Рисунок 3 – Кривая равной степени затухания
Согласно полученной кривой kp
=2.663 при ki
=0. Значит коэффициент передачи П-регулятора kP
=2.663.
Построим переходную характеристику САР с П-регулятором.
Script 3:
>> Wop=tf([0.9 7 2.2],[336 146 21 1]);
>> Wap1=tf(2.663);
>> W1=series(Wap1,Wop)
Transfer function:
2.397 s^2 + 18.64 s + 5.859
----------------------------
336 s^3 + 146 s^2 + 21 s + 1
>> Fi1=feedback(W1,1)
Transfer function:
2.397 s^2 + 18.64 s + 5.859
-------------------------------------
336 s^3 + 148.4 s^2 + 39.64 s + 6.859
>> step(Fi1);grid
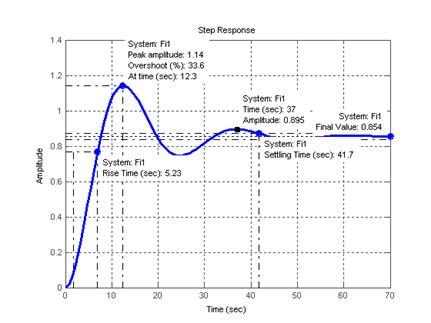
Рисунок 4 – Переходная характеристика САР с П-регулятором
Определяем полученную в результате синтеза степень затухания по формуле
 |
( |
Script 4:
>> ((1.14-0.854)-(0.895-0.854))/(1.14-0.854)
ans = 0.8566
Полученная степень затухания примерно совпадает с заданной, значит коэффициент передачи выбран верно.
Передаточная функция ПИ-регулятора определяется по формуле
Коэффициенты kp
и ki
определяем по кривой равной степени затухания (рисунок 3). kp
= 1.21 и ki
= 0.098. Тогда передаточная функция ПИ-регулятора будет иметь вид
 .
Построим переходную характеристику САР с ПИ-регулятором.
Script 5:
>> Wop=tf([0.9 7 2.2],[336 146 21 1]);
>> Wap2=tf([1.21 0.098],[1 0]);
>> W2=series(Wap2,Wop)
Transfer function:
1.089 s^3 + 8.558 s^2 + 3.348 s + 0.2156
----------------------------------------
336 s^4 + 146 s^3 + 21 s^2 + s
>> Fi2=feedback(W2,1)
Transfer function:
1.089 s^3 + 8.558 s^2 + 3.348 s + 0.2156
--------------------------------------------------
336 s^4 + 147.1 s^3 + 29.56 s^2 + 4.348 s + 0.2156
>> step(Fi2);grid
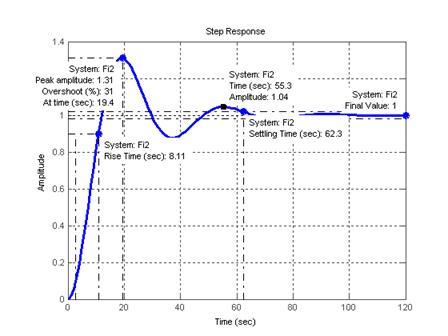
Рисунок 5 – Переходная характеристика САР с ПИ-регулятором
По формуле (3) определяем степень затухания ψ
Script 6:
>> ((1.31-1)-(1.04-1))/(1.31-1)
ans = 0.8710
Полученная степень затухания примерно совпадает с заданной, значит параметры настройки регулятора выбраны верно.
Передаточная функция ПИД-регулятора определяется по формуле
 , |
где  .
Т. к. для ПИД-регулятора необходимо определить три коэффициента, то построим кривую равной степени затухания с учетом времени дифференцирования  .
Script 7:
>> w=0.15:0.001:0.26;
>> Wex=(0.9*((j-m).*w).^2+7*(j-m).*w+2.2)./ ...
(336*((j-m).*w).^3+146*((j-m).*w).^2+21*(j-m).*w+1);
>> Win=1./Wex;
>> R=real(Win);
>> I=imag(Win);
>> Ki=w*(m^2+1).*(I+w*2.04);
>> Kp=m.*I-R+2*m.*w*2.04;
>> plot(Kp,Ki);xlabel('Axis Kp');ylabel('Axis Ki');grid
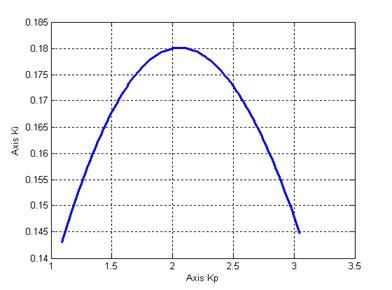
Рисунок 6 – Кривая равной степени затухания
Коэффициенты kp
и ki
определяем по кривой равной степени затухания (рисунок 6). kp
= 2.05 и ki
= 0.18. Тогда передаточная функция ПИД-регулятора будет иметь вид
 .
Построим переходную характеристику САР с ПИД-регулятором.
Script 8:
>> Wop=tf([0.9 7 2.2],[336 146 21 1]);
>> Wap3=tf([2.04 2.05 0.18],[1 0]);
>> W3=series(Wap3,Wop)
Transfer function:
1.836 s^4 + 16.13 s^3 + 19 s^2 + 5.77 s + 0.396
-----------------------------------------------
336 s^4 + 146 s^3 + 21 s^2 + s
>> Fi3=feedback(W3,1)
Transfer function:
1.836 s^4 + 16.13 s^3 + 19 s^2 + 5.77 s + 0.396
-----------------------------------------------
337.8 s^4 + 162.1 s^3 + 40 s^2 + 6.77 s + 0.396
>> step(Fi3);grid
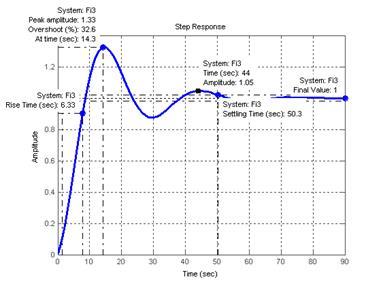
Рисунок 7 – Переходная характеристика САР с ПИД-регулятором
По формуле (3) определяем степень затухания ψ
Script 9:
>> ((1.33-1)-(1.05-1))/(1.33-1)
ans =0.8485
Полученная степень затухания примерно совпадает с заданной, значит параметры настройки регулятора выбраны верно.
По переходным характеристикам, полученным в пунктах 1.3-1.5 определим следующие показатели качества:
ymax
1
– амплитуда первого максимума;
ymax
2
– амплитуда второго максимума;
yуст
– установившееся значение;
σ – перерегулирование;
ε – статическое отклонение.
tp
– время регулирования;
tn
– время нарастания;
tmax
– время достижения первого максимума;
æ – декремент затухания;
T – период колебаний;
ω – частота колебаний;
n – колебательность;
Таблица 1 – Показатели качества САР по каналу управляющего воздействия
| Регуляторы |
ymax
1
|
ymax
2
|
yуст
|
σ |
ε |
tp
|
tn
|
tmax
|
æ |
T |
ω |
n |
| П |
1.14 |
0.895 |
0.854 |
33.6 |
0.146 |
41.7 |
5.23 |
12.3 |
6.98 |
24.7 |
0.25 |
1.5 |
| ПИ |
1.31 |
1.04 |
1 |
31 |
0 |
62.3 |
8.11 |
19.4 |
7.75 |
35.9 |
0.175 |
1.5 |
| ПИД |
1.33 |
1.05 |
1 |
32.6 |
0 |
50.3 |
6.33 |
14.3 |
6.6 |
29.7 |
0.21 |
1.5 |
Декремент затухания и частоту колебаний определяем по формулам
æ
|
 |
Проанализировав полученные данные, можно сделать вывод, что каждая САР обладает своим рядом преимуществ и недостатков. САР с П-регулятором имеет наименьшее отклонение по амплитуде, но обладает статической ошибкой. У САР с ПИ-регулятором нет статической ошибки, но она имеет наибольшее время регулирования. САР с ПИД-регулятором наиболее быстродействующая, но она также обладает и наибольшим перерегулированием.
Для оценки качества САР по каналу возмущающего воздействия преобразуем структурную схему САР (рисунок 8).
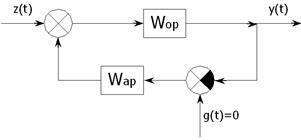
Рисунок 8 – Структурная схема преобразованной САР
Определим передаточную функцию САР по возмущающему каналу:
Script 10:
>> Fiz1=feedback(Wop,Wap1)
Transfer function:
0.9 s^2 + 7 s + 2.2
-------------------------------------
336 s^3 + 148.4 s^2 + 39.64 s + 6.859
>> Fiz2=feedback(Wop,Wap2)
Transfer function:
0.9 s^3 + 7 s^2 + 2.2 s
--------------------------------------------------
336 s^4 + 147.1 s^3 + 29.56 s^2 + 4.348 s + 0.2156
>> Fiz3=feedback(Wop,Wap3)
Transfer function:
0.9 s^3 + 7 s^2 + 2.2 s
-----------------------------------------------
337.8 s^4 + 162.1 s^3 + 40 s^2 + 6.77 s + 0.396
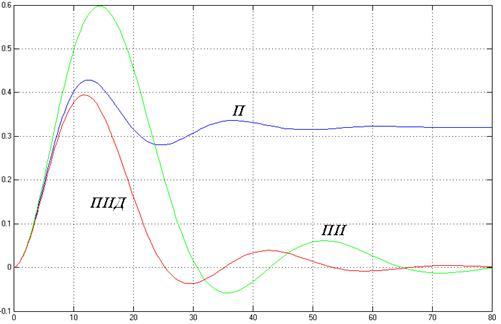
Рисунок 8 – Переходные характеристики САР по каналу возмущающего воздействия
Таблица 2 – Показатели качества САР по каналу возмущающего воздействия
| Регуляторы |
ymax
1
|
ymax
2
|
yуст
|
σ |
ε |
tp
|
tn
|
tmax
|
æ |
T |
ω |
n |
| П |
0.429 |
0.336 |
0.321 |
33.6 |
0.321 |
41.7 |
5.23 |
12.3 |
0.86 |
24.6 |
0.26 |
1.5 |
| ПИ |
0.598 |
0.061 |
0 |
¥ |
0 |
73.5 |
0 |
14.3 |
0.898 |
37.7 |
0.167 |
2 |
| ПИД |
0.39 |
0.04 |
0 |
¥ |
0 |
49 |
0 |
14 |
0.897 |
30 |
0.21 |
1.5 |
Проанализировав полученные данные, можно сделать вывод, что по каналу возмущающего воздействия САР с П-регулятором имеет наименьшее отклонение по амплитуде, но обладает статической ошибкой. У САР с ПИ-регулятором нет статической ошибки, но она имеет наибольшее время регулирования. САР с ПИД-регулятором наиболее быстродействующая.
Для оценки запаса устойчивости применим логарифмический критерий. При проектировании САР рекомендуемый запас устойчивости по амплитуде ∆L>6 Дб, по фазе ∆φ>300
.
Script 11:
>> [Gm1,Pm1]=margin(W1);
>> [Gm2,Pm2]=margin(W2);
>> [Gm3,Pm3]=margin(W3);
>> [20*log10(Gm1),Pm1]
ans =
Inf 41.6235
>> [20*log10(Gm2),Pm2]
ans =
Inf 36.7183
>> [20*log10(Gm3),Pm3]
ans =
Inf 36.0532
Таблица 3 – Запас устойчивости САР
| Регуляторы |
∆L |
∆φ |
| П |
¥ |
41.6 |
| ПИ |
¥ |
36.7 |
| ПИД |
¥ |
36.1 |
Проанализировав полученные данные, можно сделать вывод, что необходимым запасом устойчивости и по амплитуде, и по фазе обладают все САР.
3.1.1 Разработка математической модели типа «вход-состояние-выход»
Основная передаточная функция САР с П-регулятором была получена в п. 1.3. Она имеет вид:
 ,
где  ,
Порядок характеристического полинома  . Для данной САР выбираем вторую управляемую форму или управляемое каноническое представление (УКП). Математическая модель САР описывается следующей системой векторно-матричных уравнений:
где
Script 12:
>> b2=2.397;b1=18.64;b0=5.859;
>> a3=336;a2=148.4;a1=39.64;a0=6.859;
>> A1=[0 1 0;0 0 1;-a0/a3 -a1/a3 -a2/a3];
>> B1=[0;0;1];
>> C1=[b0/a3 b1/a3 b2/a3];
>> D1=0;
>> sys1=ss(A1,B1,C1,D1)
a =
x1 x2 x3
x1 0 1 0
x2 0 0 1
x3 -0.02041 -0.118 -0.4417
b =
u1
x1 0
x2 0
x3 1
c =
x1 x2 x3
y1 0.01744 0.05548 0.007134
d =
u1
y1 0
Continuous-time model.
>> step(sys1);grid
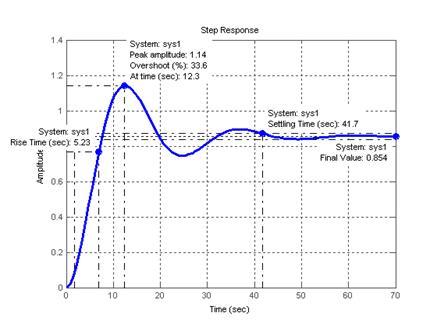
Рисунок 9 – Переходная характеристика САР с П-регулятором
При исользовании модели «вход-выход» и модели «вход-состояние-выход» были получены абсолютно идентичные переходные характеристики (рисунки 4 и 9), следовательно, модель «вход-состояние-выход» для САР с П-регулятором рассчитана, верно.
3.1.2 Структурная схема САР с П-регулятором
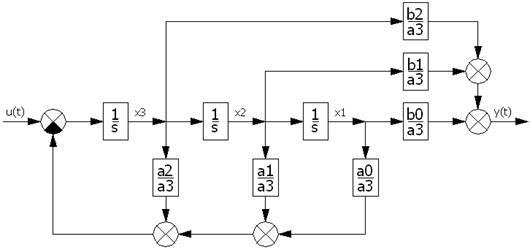
Рисунок 10 – Структурная схема САР с П-регулятором
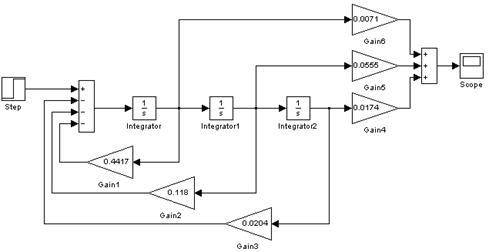
Рисунок 11 – Схема s-модели САР с П-регулятором
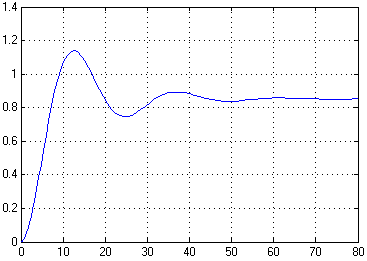
Рисунок 12 – Переходная характеристика САР с П-регулятором
Переходная характеристика, полученная по s-модели САР с П-регулятором с помощью пакета Simulink системы MATLAB совпадает с полученными ранее переходными характеристиками, значит s-модель построена верно.
3.1.3 Оценка управляемости САР с П-регулятором
Оценку управляемости САР будем проводить с помощью критерия управляемости Калмана. Матрица управляемости имеет следующий вид:
Script 13:
>> Y1=[B1 A1*B1 A1^2*B1]
Y1 =
0 0 1.0000
0 1.0000 -0.4417
1.0000 -0.4417 0.0771
>> rY1=rank(Y1)
rY1 =
3
>> dY1=det(Y1)
dY1 =
-1
Согласно критерию управляемости Калмана исследуемая система полностью управляема, так как ранг матрицы управляемости равен размеру вектора переменных состояния. Определитель матрицы управляемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью управляема.
3.1.4 Оценка наблюдаемости САР с П-регулятором
Оценку наблюдаемости САР будем проводить с помощью критерия наблюдаемости Калмана. Матрица наблюдаемости имеет следующий вид:
Script 14:
>> H1=[C1; C1*A1; C1*A1^2]
H1 =
0.0174 0.0555 0.0071
-0.0001 0.0166 0.0523
-0.0011 -0.0063 -0.0065
>> rH1=rank(H1)
rH1 =3
>> dH1=det(H1)
dH1 =
8.5991e-007
Согласно критерию наблюдаемости Калмана исследуемая система полностью наблюдаема, так как ранг матрицы наблюдаемости равен размеру вектора переменных состояния. Определитель матрицы наблюдаемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью наблюдаема.
3.2.1 Разработка математической модели типа «вход-состояние-выход»
Основная передаточная функция САР с ПИ-регулятором была получена в п. 1.4. Она имеет вид:
 ,
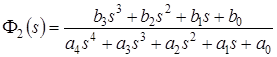где  ,
 .
Порядок характеристического полинома  . Для данной САР выбираем вторую управляемую форму или управляемое каноническое представление (УКП). Математическая модель САР описывается следующей системой векторно-матричных уравнений:
где
Script 15:
>> b3=1.089;b2=8.558;b1=3.348;b0=0.2156;
>> a4=336;a3=147.1;a2=29.56;a1=4.348;a0=0.2156;
>> A2=[0 1 0 0;0 0 1 0;0 0 0 1;-a0/a4 -a1/a4 -a2/a4 -a3/a4];
>> B2=[0;0;0;1];
>> C2=[b0/a4 b1/a4 b2/a4 b3/a4];
>> D2=0;
>> sys2=ss(A2,B2,C2,D2)
a =
x1 x2 x3 x4
x1 0 1 0 0
x2 0 0 1 0
x3 0 0 0 1
x4 -0.0006417 -0.01294 -0.08798 -0.4378
b =
u1
x1 0
x2 0
x3 0
x4 1
c =
x1 x2 x3 x4
y1 0.0006417 0.009964 0.02547 0.003241
d =
u1
y1 0
Continuous-time model.
>> step(sys2);grid
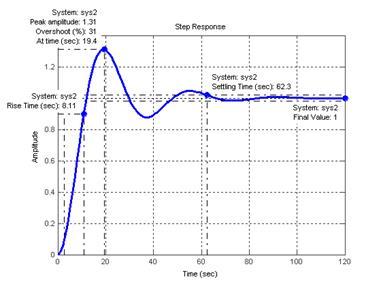
Рисунок 13 – Переходная характеристика САР с ПИ-регулятором
При исользовании модели «вход-выход» и модели «вход-состояние-выход» были получены абсолютно идентичные переходные характеристики (рисунки 5 и 13), следовательно, модель «вход-состояние-выход» для САР с ПИ-регулятором рассчитана верно.
3.2.2 Структурная схема САР с ПИ-регулятором
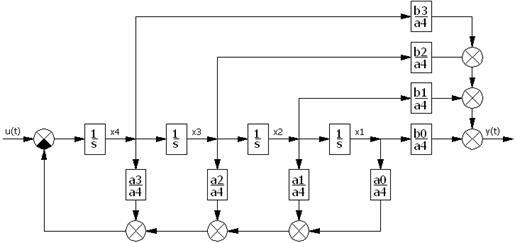
Рисунок 14 – Структурная схема САР с ПИ-регулятором
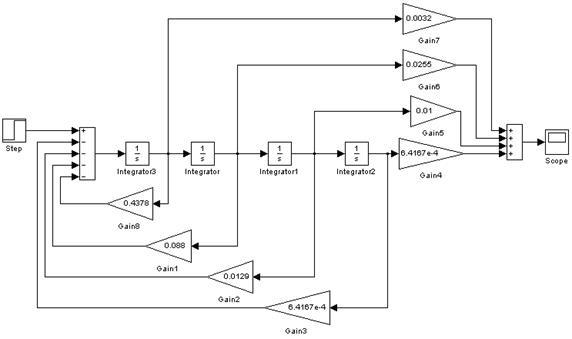
Рисунок 15 – Схема s-модели САР с ПИ-регулятором
Рисунок 16 – Переходная характеристика САР с ПИ-регулятором
Переходная характеристика, полученная по s-модели САР с ПИ-регулятором с помощью пакета Simulink системы MATLAB совпадает с полученными ранее переходными характеристиками, значит s-модель построена, верно.
3.2.3 Оценка управляемости САР с ПИ-регулятором
Оценку управляемости САР будем проводить с помощью критерия управляемости Калмана. Матрица управляемости имеет следующий вид:
Script 16:
>> Y2=[B2 A2*B2 A2^2*B2 A2^3*B2]
Y2 =
0 0 0 1.0000
0 0 1.0000 -0.4378
0 1.0000 -0.4378 0.1037
1.0000 -0.4378 0.1037 -0.0198
>> rY2=rank(Y2)
rY2 =4
>> dY2=det(Y2)
dY2 = 1
Согласно критерию управляемости Калмана исследуемая система полностью управляема, так как ранг матрицы управляемости равен размеру вектора переменных состояния. Определитель матрицы управляемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью управляема.
3.2.4 Оценка наблюдаемости САР с ПИ-регулятором
Оценку наблюдаемости САР будем проводить с помощью критерия наблюдаемости Калмана. Матрица наблюдаемости имеет следующий вид:
Script 17:
>> H2=[C2; C2*A2; C2*A2^2; C2*A2^3]
H2 =
0.0006 0.0100 0.0255 0.0032
-0.0000 0.0006 0.0097 0.0241
-0.0000 -0.0003 -0.0015 -0.0009
0.0000 -0.0000 -0.0002 -0.0011
>> rH2=rank(H2)
rH2 =4
>> dH2=det(H2)
dH2 = -1.2054e-014
Согласно критерию наблюдаемости Калмана исследуемая система полностью наблюдаема, так как ранг матрицы наблюдаемости равен размеру вектора переменных состояния. Определитель матрицы наблюдаемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью наблюдаема.
3.3.1 Разработка математической модели типа «вход-состояние-выход»
Основная передаточная функция САР с ПИД-регулятором была получена в п. 1.5. Она имеет вид:
 ,
где  ,
 .
Порядок характеристического полинома  . Математическая модель данной САР описывается следующей системой векторно-матричных уравнений:
где
 ,
 ,
 ,
 ,
 .
Script 18:
>> b4=1.836;b3=16.13;b2=19;b1=5.77;b0=0.396;
>> a4=337.8;a3=162.1;a2=40;a1=6.77;a0=0.396;
>> v0=b4/a4;
>> v1=(b3-v0*a3)/a4;
>> v2=(b2-v0*a2-v1*a3)/a4;
>> v3=(b1-v0*a1-v1*a2-v2*a3)/a4;
>> v4=(b0-v0*a0-v1*a1-v2*a2-v3*a3)/a4;
>> A3=[0 1 0 0;0 0 1 0;0 0 0 1;-a0/a4 -a1/a4 -a2/a4 -a3/a4];
>> B3=[v1;v2;v3;v4];
>> C3=[1 0 0 0];
>> D3=v0;
>> sys3=ss(A3,B3,C3,D3)
a =
x1 x2 x3 x4
x1 0 1 0 0
x2 0 0 1 0
x3 0 0 0 1
x4 -0.001172 -0.02004 -0.1184 -0.4799
b =
u1
x1 0.04514
x2 0.03394
x3 -0.00466
x4 -0.001521
c =
x1 x2 x3 x4
y1 1 0 0 0
d =
u1
y1 0.005435
Continuous-time model.
>> step(sys3);grid
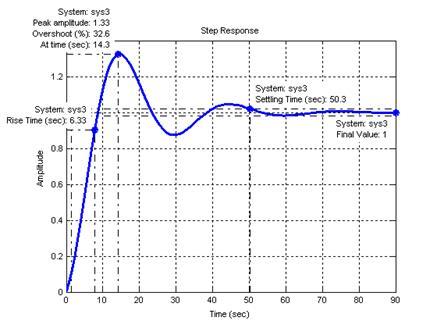
Рисунок 17 – Переходная характеристика САР с ПИД-регулятором
При исользовании модели «вход-выход» и модели «вход-состояние-выход» были получены абсолютно идентичные переходные характеристики (рисунки 7 и 17), следовательно, модель «вход-состояние-выход» для САР с ПИД-регулятором рассчитана, верно.
3.3.2 Структурная схема САР с ПИД-регулятором
Рисунок 18 – Структурная схема САР с ПИД-регулятором
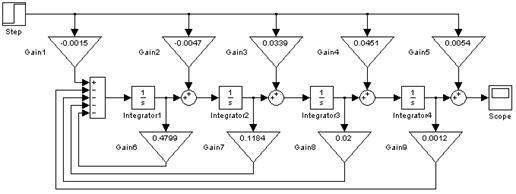
Рисунок 19 – Схема s-модели САР с ПИД-регулятором
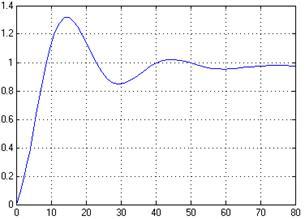
Рисунок 20 – Переходная характеристика САР с ПИД-регулятором
Переходная характеристика, полученная по s-модели САР с ПИД-регулятором с помощью пакета Simulink системы MATLAB совпадает с полученными ранее переходными характеристиками, значит s-модель построена, верно.
3.3.3 Оценка управляемости САР с ПИД-регулятором
Оценку управляемости САР будем проводить с помощью критерия управляемости Калмана. Матрица управляемости имеет вид (15):
Script 19:
>> Y3=[B3 A3*B3 A3^2*B3 A3^3*B3]
Y3 =
0.0451 0.0339 -0.0047 -0.0015
0.0339 -0.0047 -0.0015 0.0005
-0.0047 -0.0015 0.0005 -0.0000
-0.0015 0.0005 -0.0000 -0.0000
>> rY3=rank(Y3)
rY3 =4
>> dY3=det(Y3)
dY3 = -1.6937e-014
Согласно критерию управляемости Калмана исследуемая система полностью управляема, так как ранг матрицы управляемости равен размеру вектора переменных состояния. Определитель матрицы управляемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью управляема.
3.3.4 Оценка наблюдаемости САР с ПИД-регулятором
Оценку наблюдаемости САР будем проводить с помощью критерия наблюдаемости Калмана. Матрица наблюдаемости имеет следующий вид:
Script 20:
>> H3=[C3;C3*A3;C3*A3^2;C3*A3^3]
H3 =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> rH3=rank(H3)
rH3 =4
>> dH3=det(H3)
dH3 = 1
Согласно критерию наблюдаемости Калмана исследуемая система полностью наблюдаема, так как ранг матрицы наблюдаемости равен размеру вектора переменных состояния. Определитель матрицы наблюдаемости не равен нулю, значит, она является не вырожденной. Это также означает, что САУ полностью наблюдаема.
4.1
Описание нелинейнойСАР
Cтруктурная схема нелинейной САР представлена на рисунке 21.
Рисунок 21 – Структурная схема нелинейной САР
Роль АР выполняет ПИ-регулятор с передаточной функцией, полученной в п. 1.4:
 .
Нелинейное звено – звено с насыщением (ограничением), статическая характеристика звена изображена на рисунке 22.
Рисунок 22 – Статическая характеристика нелинейного элемента
Параметры звена с насыщением:  .
Для оценки возможности и устойчивости автоколебаний в нелинейной САР по методу Гольдфарба необходимо линеаризовать систему. Применим к нелинейному элементу гармоническую линеаризацию. Тогда передаточная функция звена с насыщением будет иметь вид:
 , |
где  ,
 при  , т. е.  .
Таким образом, передаточная функция нелинейного элемента принимает вид:
 .
Условие возникновения автоколебаний:
 , |
или
 , |
где  ,
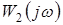 – передаточная функция линейной части разомкнутой САР с ПИ-регулятором (см. п. 1.4).
Уравнение (19) решаем графически. Для этого необходимо построить на одной комплексной плоскости годограф Найквиста линейной части 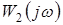и годограф Гольдфарба  .
Script 21:
>> A=0.001:0.001:5;
>> Wnon=(2./pi).*(asin(2.4./A)+(2.4./A).*sqrt(1-5.76./A.^2));
>> Z=-1./(Wnon);
>> Re=real(Z);
>> Im=imag(Z);
>> w=0.1:0.01:1;
>> W2=(b3*(j*w).^3+b2*(j*w).^2+b1*(j*w)+b0)./ ...
(a4*(j*w).^4+a3*(j*w).^3+a2*(j*w).^2+a1*(j*w));
>> re=real(W2);
>> im=imag(W2);
>> plot(re,im,Re,Im);grid
Построенные в результате выполнения Script 21 годографы приведены на рисунке 23. На рисунке 24 показана увеличенно область, в которой годографы могут пересекаться. Видно, что годографы не пересекаются, значит автоколебания в системе невозможны.
Рисунок 23 – Годографы линеаризованной САР
Рисунок 24 – Годографы линеаризованной САР (увеличенно)
Для подтверждения сделанных выводов построим модель САР в Simulink. Схема модели изображена на рисунке 25, переходная характеристика, полученная с помощью этой модели – на рисунке 26.
Рисунок 25 – Схема s-модели нелинейной САР
Рисунок 26 – Переходная характеристика нелинейной САР
Очевидно, что автоколебаний в системе нет, значит, расчеты и вывод о том, что в системе невозможны автоколебания, были сделаны верно.
В ходе выполнения курсового проекта был произведен анализ объекта регулирования, построены кривая разгона ОР.
В результате проведения необходимых расчетов были определены оптимальные параметры настройки П, ПИ, ПИД-регуляторов, запас устойчивости систем, оценено качество переходных процессов САР с П, ПИ, ПИД-регуляторами. Также был проведен анализ наблюдаемости и управляемости САР: система со всеми тремя регуляторами оказалась полностью наблюдаемой и управляемой.
Для случая, когда регулирующий орган имеет нелинейную характеристику был проведен анализ на возможность возникновения автоколебаний в нелинейной системе регулирования методом Гольдфарба. Установлено, что автоколебания в системе невозможны. Невозможность автоколебаний подтверждена моделированием системы в Simulink.
1. Линейные и нелинейные системы управления: Методические указания и задания на курсовой проект по курсу «Теория управления» для студентов дневной и заочной форм обучения специальности 2102 – Автоматизация технологических процессов и производств / Составители С. Г. Денисенко, Ю. Е. Кичкарь. Кубан. гос. технол. ун-т; - Краснодар: Изд-во КубГТУ, 2000. – 22 с.
2. MATLAB 6/6.1/6.5 + Simulink 4/5. Основы применения / Дьяконов В. П. М.: СОЛОН-Пресс, 2004. 768 с.
|
