Аннотация
В работе производится моделирование вихретокового контроля с помощью системы двух первичных (намагничивающих) и одной вторичной (измерительной) катушек. Исследуется зависимость информативного сигнала при разных частотах для различных форм дефектов, а так же их размеров (глубины, раскрытие дефекта). Далее рассчитываются информативные признаки, по которым определяются параметры дефекта. Полученные признаки используются при выполнении корреляционного анализа, по результатам которого делается вывод о наиболее полезных признаках. После проведения корреляционного анализа строится интеллектуальная нейронная сеть, обучается и тестируется. Цель работы выбрать наиболее подходящую структуру нейронной сети для дальнейшего использования ее на практике.
Работа содержит: 35 страниц, 20 иллюстраций, 4 таблицы, 2 приложения.
Введение
В электромагнитном методе неразрушающего контроля обычно используют два основных подхода к решению задачи обнаружения дефекта.
Основой первого подхода [1] к обнаружению поверхностных трещин с помощью вихревых токов является тот факт, что трещины препятствуют протеканию тока, при этом учитывается влияние скин-эффекта. В этом случае можно обнаружить те трещины, которые ориентированы вдоль линий магнитного поля. Однородные условия в контролируемом образце можно создать путем его намагничивания с помощью бесконечно длинного соленоида. Но, так как на практике любая намагничивающая катушка имеет конечную длину, следует учитывать магнитные поля рассеяния. Помимо этого стоит учитывать и размагничивающий эффект вихревых токов.
Второй подход [2] заключается в непосредственном использовании магнитного поля рассеяния, которое позволяет выявить приповерхностное изменение магнитного поля путем, например, нанесения на поверхность образца флуоресцентного (светящегося в темноте) ферромагнитного порошка. В этом случае можно обнаружить трещины, перпендикулярные линиям магнитного поля.
В данной работе исследуется особая схема расположения двух первичных (намагничивающих) катушек и одной вторичной (измерительной) катушек, при которой оба эти подхода могут проявиться вместе, а, следовательно, становится возможным получить более полную информацию о размерах дефекта. При другом расположении катушек и датчика относительно друг друга для правильного объяснения результатов очень важно понимать физику процесса. В этом случае, оказывается, удобно описывать поле с помощью математической модели. Часто применяются численные методы, где задействованы уравнения Максвелла в дифференциальной форме, включающие действительную и мнимую компоненты поля.
Сигналы, полученные в ходе моделирования данной схемы, пересчитываются в определенные информативные признаки, которые используются для построения искусственной нейронной сети, как системы, автоматически классифицирующей дефекты. Нейронные сети имеют большую популярность в различных сферах. Их успех определяется несколькими причинами, которые подробнее будут рассмотрены далее.
Актуальность поставленной задачи заключается в разработки наиболее точного метода классификации дефектов и сведение работы оператора к минимуму.
2. Вихревые токи
2.1 Первичная и вторичная катушки
Основной принцип вихретокового метода контроля можно объяснить с помощью простого примера: обнаружение поверхностных трещин в металлическом образце.
Считаем, что длинный металлический образец с круглым поперечным сечением помещен в однородное магнитное поле, линии которого направлены вдоль объекта контроля. Ввиду присутствия эффекта размагничивания образца вихревыми токами (скин-эффекта) магнитное поле в поперечном сечении не однородно. Оно гораздо сильнее у поверхности, нежели в центре, а, кроме того, в разных зонах поперечного сечения разной оказывается и фаза поля. Эта особенность зависит от частоты и физических свойств материала.
Наведенное во второй катушке (намотанной вокруг исследуемого образца) напряжение прямо пропорционально магнитному потоку в поперечном сечении этого образца. Между напряжением первичной намагничивающей катушки и напряжением, наведенным во вторичной катушке, существует разность фаз, обусловленная частотой и физическими свойствами образца.
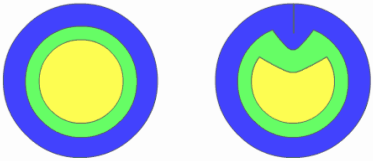
Рисунок 1. Поперечное сечение металлического образца с радиально расположенной трещиной и без трещины
Ситуация во вторичной катушке изменится, если на поверхности образца появится радиальная трещина, протяженная вдоль объекта контроля. Размагничивающее действие вихревых токов уменьшается из-за того, что эти токи не могут пересекать трещину. Соответственно, увеличивается длина пути, который проходит магнитный поток в поперечном сечении образца, что в свою очередь вызывает увеличение наведенного во вторичной обмотке напряжения. По разнице наведенных напряжений можно судить о наличии дефекта в металлическом образце. На рис.1 схематично показано магнитное поле в поперечном сечении образца с радиальной трещиной и бездефектного образца. В области над дефектом наблюдается увеличение магнитного потока. Более темная область поперечного сечения соответствует меньшей разности фаз и более сильному магнитному полю.
Согласно этим объяснениям, зафиксировать разность напряжений невозможно в том случае, когда поверхностная трещина не препятствует протеканию вихревых токов. Следовательно, мы не сможем обнаружить очень узкий поверхностный дефект, расположенный вдоль оси образца (в этом случае направление вихревых токов неизменно).
2.2 Дифференциальное (встречное) включение вторичных катушек
Изменения напряжения, наведенного во вторичной катушке (в соответствии с рис.2) очень малы, поэтому используют дифференциальное (встречное) включение двух вторичных катушек: две встречно включенные катушки наматываются вокруг образца и их выводы подключаются таким образом, чтобы наведенные напряжения вычитались друг из друга. В том случае, если между наведенными напряжениями отсутствует разница, считается, что исследуемый образец не содержит дефектов. Как показано на рис.2, если в контролируемую область внезапно попадет край дефекта, от пары катушек мгновенно сформируется сигнал. Данный способ характеризуется высокой чувствительностью к обнаружению продольных поверхностных трещин в металлических образцах.

Рисунок 2. Два встречно включенных витка пары вторичных катушек
Несмотря на то, что этот метод весьма перспективен, у него есть и свои недостатки. К примеру, если трещина однородна по всей длине образца, магнитный поток будет увеличиваться равномерно, и подобное расположение катушек не даст нам обнаружить дефект начиная с того момента, когда наведенные в обеих вторичных катушках напряжения станут равными.
Также невозможно определить и местоположение трещины на округлой поверхности образца (даже если она имеет четко выраженные начало и конец).
2.3 Радиальный магнитный поток
При контроле металлического образца с однородной трещиной, которая начинается и заканчивается в четко определенных точках, было установлено наличие других эффектов. С помощью встречного включения вторичных катушек можно зафиксировать обе эти точки. В соответствии с законами электромагнетизма, увеличение магнитного потока в поперечном сечении, вызванное слабым действием вихревых токов, может быть зафиксировано другим способом. Если магнитный поток возрастает из-за наличия поверхностной трещины, линии магнитного потока должны входить в образец откуда-то извне. Существует сильный радиальный магнитный поток, протекающий извне образца в образец, и локализованный только в точке начала трещины. Причем измеряемый радиальный поток будет пропорционален сигналу от пары вторичных катушек, включенных встречно. Измерение радиального магнитного потока, показанного на рис.3, дает также дополнительную информацию. Становится возможным определить не только расположение начала и конца трещины, но и ее расположение на округлой поверхности образца.
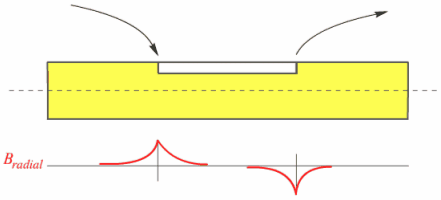
Рисунок 3. Радиальный поток, входящий в образец в начале трещины и выходящий из образца в конце трещины
2.4 Поток магнитного рассеивания
Также стоит сказать о потоке магнитного рассеяния, который используется для обнаружения поверхностных трещин в намагниченных ферромагнитных образцах.
Физический принцип данного явления можно объяснить для двумерного случая обнаружения поверхностной трещины, когда однородное (или неоднородное) поле пересекает поверхностную трещину в ферромагнитной пластине (рис.4).

Рисунок 4. Поток магнитного рассеяния для двумерного случая в поперечном сечении ферромагнитной пластины
Считается, что однородное магнитное поле распространяется слева направо. Вблизи дефекта поток разделяется на две части. Одна часть потока пытается обогнуть трещину путем прохождения снизу, в то время как другая выходит за пределы материала и огибает трещину по воздуху, затем возвращаясь в образец вблизи правого края дефекта. Этот эффект наблюдается в ферромагнитных материалах и, в том случае, если поверхность пластины покрыта ферромагнитным порошком, становится возможным увидеть образующееся поле невооруженным глазом.
В случае, когда магнитное поле в ферромагнитном материале вызывается переменным током, дело обстоит примерно так же. Только в отличие от магнитного порошка для обнаружения образующегося магнитного потока может применяться подходящая вторичная катушка.
3. Решение прямой задачи НК
3.1 Постановка задачи
Исследовать модель для обнаружения продольной и поперечной трещины с помощью следующей конфигурации первичной катушки и вторичной катушек.
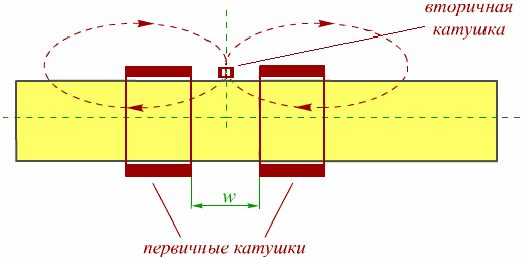
Рисунок 5. Две части намагничивающей катушки с датчиком Холла посередине
Первичная намагничивающая катушка изготовлена в виде двух одинаковых частей, удаленных друг от друга на критическое расстояние  . Между этими частями помещается вторичная катушка расположенный таким образом, чтобы наведенное напряжение вызывалось лишь радиальным магнитным потоком, протекающим через него. . Между этими частями помещается вторичная катушка расположенный таким образом, чтобы наведенное напряжение вызывалось лишь радиальным магнитным потоком, протекающим через него.
Во вторичной катушке магнитные потоки, образующиеся от двух частей первичной катушки, вычитаются друг из друга, и, если образец однородный, то распределения радиального магнитного потока не возникает, и напряжение во вторичной катушке не наводится. Однако если в образце присутствует некая трещина, которая попадает внутрь одной из первичных катушек между двумя магнитными потоками появляется разница, и появление распределения наведенного напряжения свидетельствует о наличии дефекта.
В этом случае становится возможным обнаружить узкие продольные и поперечные поверхностные трещины, присутствующие в ферромагнитном материале.
Важно правильно выбрать критическое расстояние. Если расстояние между двумя частями первичной катушки будет слишком маленьким, изменение магнитного потока будет малым, а, следовательно, малым будет и изменение радиального магнитного потока. Если же расстояние будет слишком большим, то в распределении магнитных потоков не будет наблюдаться четко выраженного импульса.
Критическое расстояние должно быть таким, чтобы информация, полученная с помощью продольного магнитного поля в образце, могла быть оптимально использована по отношению к чувствительному элементу (радиальной катушке).
4.2 COMSOLMultiphysics
COMSOL Multiphysics - это мощная интерактивная среда для моделирования и расчетов большинства научных и инженерных задач основанных на дифференциальных уравнениях в частных производных (PDE) методом конечных элементов [3]. С этим программным пакетом есть возможность расширять стандартные модели, использующие одно дифференциальное уравнение (прикладной режим) в мультифизические модели для расчета связанных между собой физических явлений. Расчет не требует глубокого знания математической физики и метода конечных элементов. Это возможно благодаря встроенным физическим режимам, где коэффициенты PDE задаются в виде понятных физических свойств и условий, таких как: электрическая проводимость, плотность тока, относительная магнитная проницаемость, частота тока и т.п. в зависимости от выбранного физического раздела. Преобразование этих параметров в коэффициенты математических уравнений происходит автоматически. Взаимодействие с программой возможно стандартным способом – через графический интерфейс пользователя (GUI), либо программированием с помощью скриптов на языке COMSOL Script или языке MATLAB.
Программа основана на системе дифференциальных уравнений в частных производных. Существует три математических способа задания таких систем:
· Коэффициентная форма, предназначенная для линейных и близких к линейным моделям;
· Генеральная форма, для нелинейных моделей;
· Слабая форма (Weakform), для моделей с PDE на границах, ребрах или для моделей, использующих условия со смешанными производными и производными по времени.
Используя эти способы, можно изменять типы анализа, включая:
· Стационарный и переходный анализ;
· Линейный и нелинейный анализ;
· Модальный анализ и анализ собственных частот.
Для решения PDE, COMSOL Multiphysics использует метод конечных элементов. Программное обеспечение запускает конечноэлементный анализ вместе с сеткой учитывающей геометрическую конфигурацию тел и контролем ошибок с использованием разнообразных численных решателей. Так как многие физические законы выражаются в форме PDE, становится возможным моделировать широкий спектр научных и инженерных явлений из многих областей физики таких как: акустика, химические реакции, диффузия, электромагнетизм, гидродинамика, фильтрование, тепломассоперенос, оптика, квантовая механика, полупроводниковые устройства, сопромат и многих других.
Кроме вышеперечисленного, программа позволяет с помощью переменных связи (coupling variables) соединять модели в разных геометриях и связывать между собой модели разных размерностей.
Для создания и расчета задачи определена следующая последовательность действий:
1. Выбор размерности модели, определение физического раздела, определение стационарности или нестационарности температурного поля;
2. Определение рабочей области и задание геометрии;
3. Ввод исходных данных, зависимости переменных от координат и времени;
4. Указываются электромагнитные свойства и начальные условия;
5. Указываются граничные условия;
6. Задаются параметры, и строится сетка;
7. Определение параметров решающего устройства, и запуск расчета;
8. Настройка режима отображения;
9. Наблюдение и анализ результатов.
3.3 Выбор физического раздела в среде COMSOLMultiphysics
Для построения и полного физического моделирования модели целесообразно выбрать двухмерную аксиальную симметрию (рис. 6). Физический раздел выбираем для решения квазистатической задачи с проводящими, магнитными и диэлектрическими материалами с направлением переменного электрического тока вдоль угловой составляющей. Данный раздел использует цилиндрическую систему координат (r, z, φ).
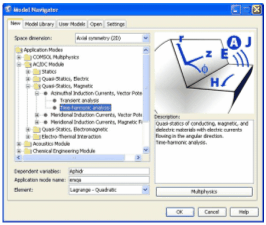
Рисунок 6. Определение физического раздела для моделирования модели
3.4 Задание геометрии
На рис. 7 изображены размеры исследуемой модели.

Рисунок 7. Геометрия модели
В среде COMSOLMultiphysicsнаша модель будет выглядеть следующим образом.

Рисунок 8. Искомая модель в среде COMSOLMultiphysics
3.5 Определение электромагнитных свойств материалов
Необходимо задать электромагнитные свойства материалов и некоторые константы, которые приведены в табл.1
| Относительная магнитная проницаемость, (μr
) |
Электрическая проводимость,
(σ, МСм/м)
|
Плотность тока,
(J, А/мм2
)
|
| Объект контроля |
1 |
2 |
0 |
| Первичные катушки |
1 |
0 |
1 |
Токи в первичных катушках должны быть сонаправлены.
Так как моделирование будет происходить для разных частот 25кГц, 100кГц, 200кГц и 400кГц, это тоже необходимо учесть при задании параметров.
3.6 Граничные условия
Для левой границы модели, с координатой r = 0 (рис. 8), определяем специальный вид граничных условий – аксиальная симметрия, что означает, что вся модель будет сконфигурирована путем вращения той части рисунка, которая лежит правее r = 0, вокруг оси z.
Магнитный потенциал на других внешних границах рисунка определяется равным нулю. Все остальные граничные условия – continuity.
3.7 Построение сетки. Получение результатов моделирования
Так как изначальное автоматическое разбиение модели нас не устраивает, мы вручную улучшаем качество разбиения интересующих нас областей, наиболее влияющих на точность решения задачи. Таким образом, получаем следующую картину.
Рисунок 9. Разбиение модели
Результатом расчета задачи является картина распределения r-той составляющей плотности магнитного потока (рис.10 и рис.11). Полученное распределение плотности магнитного потока говорит о правильности построения модели и задания всех граничных условий и свойств материалов.

Рисунок 10. Распределение плотности магнитного потока (без дефекта) на частоте 100кГц

Рисунок 11. Распределение эквипотенциальных поверхностей (без дефекта) на частоте 100кГц
4. Обработка данных
4.1 Расчетная часть
В ходе решения задачи была получена база сигналов для различных видов дефектов. Однако чтобы получить конечные результаты необходимо произвести некоторые вычисления.
Полученные результаты в среде COMSOLMultiphysics, представляющие собой массивы значений магнитной индукции, необходимо пересчитать в значения ЭДС, соответствующие сигналу с вторичной катушки.
Для начала определим магнитный поток по соответствующей формуле:

где  - площадь принимающего датчика - площадь принимающего датчика
 - значение магнитной индукции, полученные из COMSOLMultiphysics - значение магнитной индукции, полученные из COMSOLMultiphysics
Далее находим значение ЭДС:

где  - частота, на которой производились измерения - частота, на которой производились измерения
В результате получили комплексные значение ЭДС при различных параметрах: частоте, форме дефекта, глубине дефекта. Всего 400сигналов. Для расчета модели была написана программа в среде MatLab, которая работала совместно с COMSOLMultiphysics, что позволило упростить и ускорить время расчета. Текст программы приведен в приложении 1.
4.2 Результаты расчета модели
Вид годографа для прямоугольной формы дефекта, частота 25кГц, 100кГц, 200кГц, 400кГц, глубины дефектов (0.4, 0.6, 0.8, 1.0, 1.2 мм), раскрытие дефекта постоянно(0.1мм)

Рисунок 12. Годографы для дефекта прямоугольной формы с различной глубиной
Вывод:
при изменении частоты меняется угол наклона годографа, а при изменении глубины дефекта меняется амплитуда
Вид годографа для прямоугольной формы дефекта, частота 25кГц, 100кГц, 200кГц, 400кГц, раскрытие дефектов (0.1, 0.3, 0.5, 0.7, 0.9 мм), глубина дефекта постоянно(0.4мм)
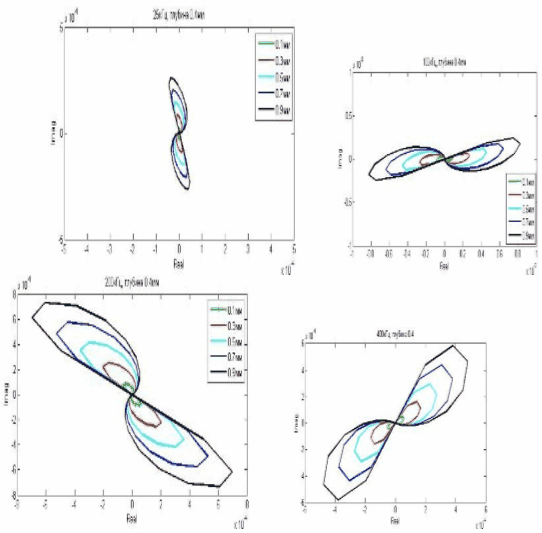
Рисунок 13. Годографы для дефекта прямоугольной формы с различным раскрытием
Вывод:
при изменении частоты меняется угол наклона годографа, а при изменении раскрытия дефекта меняется амплитуда
Зависимость амплитуды сигнала (при различных глубинах дефекта, но при постоянном раскрытии) от местоположения дефекта.
Прямоугольная форма дефекта, частота 25кГц

Рисунок 14. Сигналы для дефекта прямоугольной формы с различной глубиной
Вывод:
с увеличением глубины дефекта, амплитуда сигнала увеличивается.
Зависимость амплитуды сигнала (при различном раскрытии дефекта, но при постоянной глубине) от местоположения дефекта.
Прямоугольная форма дефекта, частота 25кГц
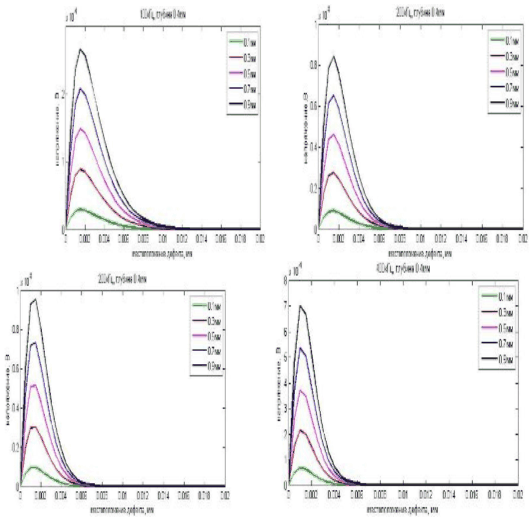
Рисунок 15. Сигналы для дефекта прямоугольной формы с различным раскрытием
Вывод:
с увеличением раскрытия дефекта, амплитуда сигнала увеличивается
4.3 Расчет информативных признаков
Для дальнейшей работы с сигналами определим по ним следующие признаки:
· F1 – максимальная резистивная составляющая;
· F2 –фаза максимальной резистивной составляющей;
· F3 – максимальная реактивная составляющая;
· F4 - фаза максимальной реактивной составляющей;
· F5 – максимальное значение ЭДС;
· F6 – фаза, соответствующая максимальному значению ЭДС;
· F7 – начальная фаза;
· F8 – конечная фаза;
· F9 – поворот фазы относительно точки с максимальной ЭДС;
· F10 – длина до точки с максимальной реактивной составляющей/ длина от точки с максимальной реактивной составляющей;
· F11 – полный размах/величина ЭДС в точке с максимальной реактивной составляющей.
На рис. 16 приведено расположение данных признаков. [5]

Рисунок 16. Схема признаков
Для расчета информативных признаков в среде MatLabбыла написана программа, автоматически считающая признаки для всех переменных параметров дефектов. Текст программы приведен в приложение 2.
Получили базу данных, состоящую из признаков, которые в дальнейшем будут использованы для корреляционного анализа, необходимых для решения обратной задачи.
5. Решение обратной задачи НК
5.1 Корреляционный анализ информативных признаков
Корреляционный анализ произведен в среде Statistica.
Statistica - это современный пакет статистического анализа, в котором реализованы все новейшие компьютерные и математические методы анализа данных. Программа предназначена для всех отраслей промышленности (бизнес, наука, обучение). В ней реализовано все возможные функции для статистической обработки данных, плюс к этому возможность построения графиков, базы данных и т.д. В программу встроен STATISTICA Visual Basic, что добавляет еще около 10000 новых функций. Синтаксис этого Basic'а полностью совместим с Microsoft Visual Basic. STATISTICA - это система статистического анализа данных, включающая широкий набор аналитических процедур и методов: - более 100 различных типов графиков, - описательные и внутригрупповые статистики, - быстрые основные статистики и блоковые статистики, - множественная регрессия, - непараметрические статистики, - разведочный анализ данных, корреляции, - общая модель дисперсионного и ковариационного анализа, - интерактивный вероятностный калькулятор, - T-критерии (и другие критерии групповых различий), - таблицы частот, сопряженности, флагов и заголовков, - анализ многомерных откликов, - подгонка распределений и многое другое.
В табл. 2 приведены результаты корреляций, интересующих нас параметров с искомыми признаками
| frequency 25 |
| F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
| width |
0,49 |
-0,26 |
0,65 |
-0,23 |
0,63 |
-0,22 |
0,03 |
0,01 |
-0,04 |
0,81 |
0,63 |
| depth |
0,58 |
-0,69 |
0,54 |
-0,85 |
0,54 |
-0,84 |
-0,42 |
0,33 |
0,57 |
0,34 |
0,55 |
| frequency 100 |
| F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
| width |
0,72 |
-0,20 |
0,46 |
-0,25 |
0,59 |
-0,14 |
0,05 |
0,07 |
0,05 |
0,70 |
0,59 |
| depth |
0,49 |
-0,89 |
0,59 |
-0,83 |
0,54 |
-0,90 |
-0,35 |
0,46 |
-0,56 |
0,50 |
0,56 |
| frequency 200 |
| F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
| width |
0,57 |
-0,13 |
0,47 |
-0,10 |
0,54 |
-0,13 |
0,04 |
0,08 |
-0,06 |
0,63 |
0,54 |
| depth |
0,57 |
-0,92 |
0,43 |
-0,76 |
0,54 |
-0,93 |
-0,33 |
0,48 |
-0,70 |
0,55 |
0,56 |
| frequency 400 |
| F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
| width |
0,38 |
-0,07 |
0,51 |
-0,08 |
0,44 |
-0,07 |
0,03 |
0,08 |
-0,09 |
0,51 |
0,44 |
| depth |
0,54 |
-0,92 |
0,48 |
-0,90 |
0,53 |
-0,94 |
-0,33 |
0,47 |
0,57 |
0,55 |
0,56 |
Из табл. 2 определяем наиболее коррелирующие признаки, на основе которых будет обучаться интеллектуальная нейронная сеть.
Классификация раскрытий дефектов будет производиться по признакам F1, F5, F10 и F11. Классификация глубин – F2, F4, F6 и F9.
5.2 Построение искусственных нейронных сетей
Нейронные сети привлекательны с интуитивной точки зрения, ибо они основаны на примитивной биологической модели нервных систем. В будущем развитие таких нейро-биологических моделей может привести к созданию действительно мыслящих компьютеров. Основными преимуществами использования нейронных сетей являются богатые возможности и простота в использовании.
Нейронные сети - исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости. В частности, нейронные сети нелинейны по своей природе. На протяжении многих лет линейное моделирование было основным методом моделирования в большинстве областей, поскольку для него хорошо разработаны процедуры оптимизации. В задачах, где линейная аппроксимация неудовлетворительна (а таких достаточно много), линейные модели работают плохо. Кроме того, нейронные сети справляются с "проклятием размерности", которое не позволяет моделировать линейные зависимости в случае большого числа переменных. В этом заключаются богатые возможности нейронных сетей.
Простота в использовании состоит в том, что нейронные сети учатся на примерах. Пользователь нейронной сети подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает структуру данных. При этом от пользователя, конечно, требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты, однако уровень знаний, необходимый для успешного применения нейронных сетей, гораздо скромнее, чем, например, при использовании традиционных методов статистики.
Основными этапами решения задачи являются:
1. Сбор данных для обучения
2. Подготовка и нормализация данных
3. Выбор топологии сети
4. Экспериментальный подбор характеристик сети
5. Экспериментальный подбор параметров обучения
6. Собственно обучение
7. Проверка адекватности обучения
8. Корректировка параметров, окончательное обучение
9. Вербализация сети с целью дальнейшего использования
На данном этапе уже решены первые два пункта. Рассмотрим подробнее остальные этапы.
Выбирать тип сети следует исходя из постановки задачи и имеющихся данных для обучения. Для обучения с учителем требуется наличие для каждого элемента выборки «экспертной» оценки. Иногда получение такой оценки для большого массива данных просто невозможно. В этих случаях естественным выбором является сеть, обучающаяся без учителя, например, самоорганизующаяся карта Кохонена
или нейронная сеть Хопфилда. При решении других задач, таких как прогнозирование временных рядов, экспертная оценка уже содержится в исходных данных и может быть выделена при их обработке. В этом случае можно использовать многослойный персептрон. В нашем случае стоит задача регрессии и нам подходят несколько типов сетей: многослойный персептрон, сеть радиальных базисных функций или вероятностная нейронная сеть.
После выбора общей структуры нужно экспериментально подобрать параметры сети. Для сетей, подобных персептрону, это будет число слоев, число блоков в скрытых слоях, наличие или отсутствие обходных соединений, передаточные функции нейронов. При выборе количества слоев и нейронов в них следует исходить из того, что способности сети к обобщению тем выше, чем больше суммарное число связей между нейронами. С другой стороны, число связей ограничено сверху количеством записей в обучающих данных.
После выбора конкретной топологии, необходимо выбрать параметры обучения нейронной сети. От правильного выбора параметров зависит не только то, насколько быстро ответы сети будут сходиться к правильным ответам. Например, выбор низкой скорости обучения увеличит время схождения, однако иногда позволяет избежать паралича сети. Увеличение момента обучения может привести как к увеличению, так и к уменьшению времени сходимости, в зависимости от формы поверхности ошибки. Исходя из такого противоречивого влияния параметров, можно сделать вывод, что их значения нужно выбирать экспериментально, руководствуясь при этом критерием завершения обучения, например, минимизация ошибки или ограничение по времени обучения).
В процессе обучения сеть в определенном порядке просматривает обучающую выборку. Порядок просмотра может быть последовательным, случайным и т. д. Некоторые сети, обучающиеся без учителя, например, сети Хопфилда просматривают выборку только один раз. Другие, например сети, обучающиеся с учителем, просматривают выборку множество раз, при этом один полный проход по выборке называется эпохой обучения. При обучении с учителем набор исходных данных делят на две части — обучающую выборку и тестовые данные; принцип разделения может быть произвольным. Обучающие данные подаются сети для обучения, а проверочные используются для расчета ошибки сети (проверочные данные никогда для обучения сети не применяются). Таким образом, если на проверочных данных ошибка уменьшается, то сеть действительно выполняет обобщение. Если ошибка на обучающих данных продолжает уменьшаться, а ошибка на тестовых данных увеличивается, значит, сеть перестала выполнять обобщение и просто «запоминает» обучающие данные. Это явление называется переобучением сети или оверфиттингом. В таких случаях обучение обычно прекращают.
Даже в случае успешного, на первый взгляд, обучения сеть не всегда обучается именно тому, чего от неё хотел создатель. Таким образом, сеть «понимает» не то, что от неё требовалось, а то, что проще всего обобщить.
В ходе анализа результатов сетей мной было отдано предпочтение структуре трехслойного персептрона, так как он обладает наименьшей погрешностью обучения, его архитектура достаточно проста, а так же вероятность оверфиттинга сведена к минимуму. Далее будут приведены выбранные архитектуры сетей и их основные параметры.
5.3 Архитектуры выбранных сетей и их основные параметры
Искусственная нейронная сеть для определения глубины дефекта
Архитектура сети МП 6:6-9-1:1

Рисунок 17. Архитектура сети
| Производительность обучения |
0,193377 |
| Контрольная производительность |
0,190212 |
| Ошибка обучения |
0,054221 |
| Контрольная ошибка |
0,055778 |
| Входы |
6 |
| Скрытые(1) |
9 |
| Скрытые(2) |
0 |
| Среднее данных |
0,000800 |
| Ст. отклик данных |
0,000283 |
| Среднее ошибки |
-0,000001 |
| Ст. отклик ошибки |
0,000055 |
| Среднее абсолютной ошибки |
0,000043 |
| Отношение ст. отклик |
0,193778 |
| Корреляция |
0,981070 |
Прогнозирование
После обучения сети был проведен ряд тестовых испытаний, в ходе которых были получены следующие прогнозы:
| прогноз |
истинное значение |
| 1 |
0,000786 |
0,000700 |
| 2 |
0,000752 |
0,000700 |
| 3 |
0,000806 |
0,000900 |
| 4 |
0,000845 |
0,000900 |
| 5 |
0,000749 |
0,000700 |
Искусственная нейронная сеть для определения раскрытия дефекта
Архитектура сети МП 8:8-7-1:1
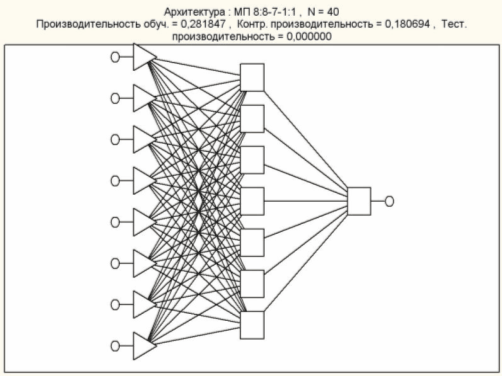
Рисунок 18. Архитектура сети
| Производительность обучения |
0,281847 |
| Контрольная производительность |
0,180694 |
| Ошибка обучения |
0,078536 |
| Контрольная ошибка |
0,051684 |
| Входы |
8 |
| Скрытые(1) |
7 |
| Скрытые(2) |
0 |
|
| Среднее данных |
0,000500 |
| Ст. отклик данных |
0,000283 |
| Среднее ошибки |
-0,000002 |
| Ст. отклик ошибки |
0,000070 |
| Среднее абсолютной ошибки |
0,000054 |
| Отношение ст. отклик |
0,245855 |
| Корреляция |
0,969317 |
Прогнозирование
| № |
прогноз |
истинное значение |
| 1 |
0,000419 |
0,000400 |
| 2 |
0,000419 |
0,000400 |
| 3 |
0,000763 |
0,000600 |
| 4 |
0,000409 |
0,000400 |
| 5 |
0,000678 |
0,000600 |
6. Погрешности
Составляющими погрешностей в данной работе являются:
· мешающие факторы
· моделирование
· расчеты
· настройка нейронных сетей
К мешающим факторам относятся: неоднородности материалов, неточное задание характеристик, неплотное прилегание датчика к объекту контроля, краевые эффекты – однако все эти факторы мы не учитываем, в силу того, что рассматриваем идеальный случай.
Погрешности моделирования складываются из неточности задания геометрии модели, шага разбиения сетки, движения дефекта (считаем, что скорость движения не превышает 0,5 м/с). Данную составляющую общей погрешности считаем не значительной, так как компьютерные средства позволяют создавать модель с высокой точностью.
В ходе получения сигналов и их обработки возникает погрешность расчетов, которая в основном обусловлена шагом, с которым мы снимаем показания. Так как этот процесс автоматизирован и рассматривается идеальная модель, эта составляющая не сильно влияет на конечный результат.
Основной составляющей погрешности является погрешность, с которой созданная нейронная сеть классифицирует дефекты и делает прогнозы. Рассмотрим ее подробнее.
Были рассмотрены три различные структуры искусственных нейронных сетей:
· многослойный персептрон
· вероятностная или обобщенная регрессионная нс
· радиальная базисная функция
Стояла задача выбрать тип сети с наименьшей погрешностью на выходе.
Погрешность определения раскрытия дефекта.

Рисунок 19
На диаграмме (рис. 19) видим, что среднее значение абсолютной погрешности многослойного персептрона минимальное. И хотя все три сети удовлетворяют требованиям к определению раскрытия, преимущество у персептрона.
В табл. 3 приведены значения средней, максимальной и минимальной погрешностей посчитанных по результатам обучения всех трех сетей. Для каждой сети было использовано 100 различных значений.
| error |
pers |
rbf |
orns |
| average |
0,054 |
0,061 |
0,063 |
| max |
0,238 |
0,253 |
0,4 |
| min |
0,001 |
0 |
0 |
Погрешность определения глубины дефекта.

Рисунок 20
Значение среднего значения абсолютной погрешности в данном случае (рис.20) минимальна у обобщенной регрессионной нейронной сети, однако ее за основу не стоит брать. В процессе выбора архитектуры сети данного типа, сеть с наименьшей ошибкой имеет 8 входов, 62 элемента на 1 скрытом слое и 2 элемента на 2 скрытом слое. Вероятность того, что сеть с такой архитектурой при имеющемся количестве сигналов для обучения, просто запомнит сигналы, а не обучится, возрастает. Поэтому для нас предпочтительнее выбрать сеть типа персептрон.
В табл. 4 приведены значения средней, максимальной и минимальной погрешностей посчитанных по результатам обучения всех трех сетей. Для каждой сети было использовано 100 различных значений.
| error |
pers |
rbf |
orns |
| average |
0,043 |
0,052 |
0,04 |
| max |
0,144 |
0,251 |
0,205 |
| min |
0 |
0,002 |
0 |
Погрешность, имеющая в данном случае интерес и максимально влияющая на результаты, является погрешностью выбранной нейронной сети. Для нас важна точность, с которой она сможет определять дефекты.
Заключение
В ходе проведенной работы была разработана, конечно элементная модель, позволяющая определять продольные и поперечные трещины. Сформирована база сигналов, по которой были рассчитаны информативные признаки, а также выявлены зависимости фазы и амплитуды от различных параметров дефекта и от нескольких частот.
С использованием информативных признаков был проведен корреляционный анализ, показавший наиболее коррелирующие признаки с параметрами дефектов. По результатам данного анализа были выбраны признаки, использованные для обучения нейронных сетей.
Полученные результаты не противоречат фундаментальным физическим законам и принципам. Погрешности лежат в допустимых пределах.
Полученные нейронные сети, могут быть использованы в дальнейших экспериментальных исследованиях по контролю продольные и поперечные дефекты труб.
Литература
1. Brudar B. How to Distinguish Surface and Subsurface Cracks // Electromagnetic NDT Methods: NDT International, Vol. 17, August 1984, p 221-223.
2. Brudar B. Magnetic Leakage Fields Calculated by the Method of Finite Differences// Electromagnetic NDT Methods: NDT International, Vol. 18, No.6, December 1985, p 353-357.
3. В.И. Егоров. Применение ЭВМ для решения задач теплопроводности. Санкт-Петербург, 2006.
4. С.Н. Бозиев. MATLAB 2006a в примерах. РГУ нефти и газа им. И.М. Губкина, 2006.
5. Song S-J. Model-based interpretation of experimental eddy current signals obtained from steam generator tubes by bobbin probe. // Insight. 2003. №5.
Приложение 1
Программа, написанная в среде MatLab для создания базы сигналов.
% параметры геометрии объекта контроля и катушек
air1H=10e-3; %толщина слоя воздуха над ОК
L=50e-3; %длинна трубы
air2H=6.5e-3; %толщина слоя воздуха под ОК
OKH=1.5e-3; %толщина трубы
OKD=8e-3; %внешний диаметр трубы
H_k=2e-3; %высота катушки
l_k=3e-3; %ширина катушки
delta_k=1e-3; %зазор между ОК и катушками
D_k = 3e-3; %расстояние между катушками
delta_izm=0.5e-3; %зазор между ОК и измерительной катушкой
r=0.01; %радиус вторичной катушки для расчетов
%Параметры геометрии дефекта по умолчанию
ld_def=1e-3; %длинна дефекта
x_def=(L/2)-ld_def; %положение центра дефекта по длине ОК
hd_def=1e-3; %глубина дефекта
fd_def=1; %форма - отношение меньшего основания к большему
%fd = 1 - прямоугольник,
%1<fd<0.01 - трапеция
%fd<0.001 -> треугольник
%Параметры эксперимента
x_start=20e-3; %начало зоны контроля
x_end=0e-3; %конец зоны контроля
x_step=-0.5e-3; %шаг съема данных
hd_start=0.4e-3; %начальная глубина дефекта
hd_end=1.2e-3; %конечная глубина дефекта
hd_step=0.2e-3; %шаг по глубине
ld_start=0.1e-3; %начальная протяженность дефекта
ld_end=1.0e-3; %конечная протяженность дефекта
ld_step=0.2e-3; %шаг по ротяженности
fd=[1,0.01,0.3,0.7]; %формы
f=[25e3,100e3,200e3,400e3]; %частоты, в герцах
f_ind=1;
x_size=size((x_start:x_step:x_end)');
x_size=x_size(1);
clear data
%figure;GEOMPLOT(fem);
% скриптэксперимента
clear data
data_ind=1;
for fd_ind = 1:size(fd')
for ld = ld_start:ld_step:ld_end
for hd = hd_start:hd_step:hd_end
for f_ind = 1:size(f')
data(data_ind,1)=data_ind;
data(data_ind,2)=fd(fd_ind);
data(data_ind,3)=ld;
data(data_ind,4)=hd;
data(data_ind,5)=f(f_ind);
x_ind=1
for x = x_start:x_step:x_end
flclear fem
% Application mode 1
clear appl
appl.mode.class ='AzimuthalCurrents';
appl.mode.type ='axi';
appl.module ='ACDC';
appl.assignsuffix ='_emqa';
clear prop
prop.analysis='transient';
appl.prop = prop;
clear pnt
pnt.I0 = {};
pnt.name = {};
pnt.ind = [];
appl.pnt = pnt;
clear bnd
bnd.chsrcdst = {};
bnd.murbnd = {};
bnd.sigmabnd = {};
bnd.eta = {};
bnd.d = {};
bnd.index = {};
bnd.Esphi = {};
bnd.pertype = {};
bnd.type = {};
bnd.A0phi = {};
bnd.name = {};
bnd.H0 = {};
bnd.Js0phi = {};
bnd.epsilonrbnd = {};
bnd.murext = {};
bnd.ind = [];
appl.bnd = bnd;
clear equ
equ.Vloop = {};
equ.Sd = {};
equ.magconstrel = {};
equ.srcpnt = {};
equ.M = {};
equ.S0 = {};
equ.Pphi = {};
equ.gporder = {};
equ.coordOn = {};
equ.sigma = {};
equ.name = {};
equ.epsilonr = {};
equ.rOn = {};
equ.dr = {};
equ.cporder = {};
equ.mur = {};
equ.normfH = {};
equ.Br = {};
equ.init = {};
equ.Stype = {};
equ.Drphi = {};
equ.R0 = {};
equ.elconstrel = {};
equ.fH = {};
equ.v = {};
equ.Jephi = {};
equ.usage = {};
equ.srcaxis = {};
equ.user = {};
equ.ind = [];
appl.equ = equ;
fem.appl{1} = appl;
fem.sdim = {'r','z'};
fem.frame = {'ref'};
fem.border = 1;
clear units;
units.basesystem ='SI';
fem.units = units;
air1 = rect2(air1H,L,'base','center', 'pos', [air1H/2+OKD 0]);
OK = rect2(OKH,L,'base','center','pos', [-(OKH/2)+OKD 0]);
air2 = rect2(air2H,L, 'base','center','pos', [-(OKH+air2H/2)+OKD 0]);
kat1 = rect2(H_k,l_k, 'base','center','pos', [delta_k+(H_k/2)+OKD -((D_k/2)+(l_k/2))]);
kat2 = rect2(H_k,l_k, 'base','center','pos', [delta_k+(H_k/2)+OKD ((D_k/2)+(l_k/2))]);
p1=point2(OKD+delta_izm,0);
defect = geomcoerce('solid',{curve2([0+OKD-OKH 0+OKD-OKH],[x-(ld/2) x+(ld/2)]),...
curve2([0+OKD-OKH hd+OKD-OKH],[x+(ld/2) x+(ld*fd(fd_ind)/2)]),...
curve2([hd+OKD-OKH hd+OKD-OKH],[x+(ld*fd(fd_ind)/2) x-(ld*fd(fd_ind)/2)]),...
curve2([hd+OKD-OKH 0+OKD-OKH],[x-(ld*fd(fd_ind)/2) x-(ld/2)])});
clear s p
p.objs={p1};
p.name={'p1'};
s.objs={air1,air2,OK,kat1,kat2,defect};
s.name={'air1','air2','OK','kat1','kat2','defect'};
draw=struct('s',s,'p',p);
fem.geom = geomcsg(draw);
fem.mesh=meshinit(fem,...
'hmax',0.5e-3,...
'hmaxvtx',[11,0.05e-3],...
'hmaxedg',[4,0.2e-3,6,0.0001,7,0.0001,8,0.2e-3,9,0.0001,11,0.0001,12,0.2e-3,15,0.0001,16,0.0001,17,0.0001,18,0.0001,19,0.0001,20,0.0001,21,0.0001,22,0.0001],...
'hmaxsub',[2,0.2e-3]);
% Application mode 1
clear appl
appl.mode.class ='AzimuthalCurrents';
appl.mode.type ='axi';
appl.dim = {'Aphi','redAphi'};
appl.sdim = {'x','z','y'};
appl.module ='ACDC';
appl.sshape = 2;
appl.assignsuffix ='_emqa';
clear prop
prop.analysis='harmonic';
appl.prop = prop;
clear bnd
bnd.type = {'A0','cont','ax'};
bnd.ind = [3,1,1,2,1,2,2,2,2,1,2,2,1,1,2,2,2,2,2,2,2,2,1];
appl.bnd = bnd;
clear equ
equ.sigma = {0,2e6,0,0};
equ.Jephi = {0,0,1e6,1e6};
equ.ind = [1,2,1,1,3,4];
appl.equ = equ;
appl.var = {'nu',f(f_ind)};
fem.appl{1} = appl;
fem.border = 1;
% Multiphysics
fem=multiphysics(fem);
% Extend mesh
fem.xmesh=meshextend(fem);
% Solve problem
fem.sol=femstatic(fem,...
'solcomp',{'Aphi'},...
'outcomp',{'Aphi'},...
'blocksize','auto',...
'ntol',1e-012);
% Integrate
data(data_ind,5+x_ind)=-postint(fem,'Br_emqa',...
'unit','T',...
'recover','off',...
'dl',11,...
'edim',0)*i*2*pi*data(data_ind,5)*pi*r^2;
data(data_ind,5+(2*x_size)-x_ind)=-data(data_ind,5+x_ind);
x_ind=x_ind+1;
end
data_ind
end
end
end
end
Приложение
2
Программа, написанная в среде MatLab для расчета информативных признаков по сформированной базе сигналов.
function [y] = prizn (P)
for k=1:5
for w=1:100
y(k,w)=P(k,w);
end;
end;
% k-ctro4ki
% w-ctolbci
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% sensitive features %%%%%%%%%%%%%%%%%%
for k=6:46
for w=1:100
Z(k,w)=P(k,w);
end;
end;
for w=1:100
for k=6:46
g(k)=Z(k,w);
end;
rez=real(g);
imz=imag(g);
rez=abs(rez);
imz=abs(imz);
mre=max(rez); %mre - max resistanse
for k=6:46
if mre==rez(k)
mr=k; %mr - max resistance index
k=46;
end
end
maxres=g(mr); %maxres - max resistance point (F1)
mrea=angle(maxres);
mrea=(180/pi)*mrea; %mrea - max resistance angle (F2)
y(6,w)=mre;
y(7,w)=mrea;
mim=max(imz); %max reactance
for k=6:46
if mim==imz(k)
mi=k; %mi - max reactance index
k=46;
end
end
maxreact=g(mi); %maxreact - max reactance point (F3)
mima=angle(maxreact);
mima=(180/pi)*mima; %mima - max reactance angle (F4)
y(8,w)=mim;
y(9,w)=mima;
absz=abs(g);
maxz=max(absz); %mabs - max impedance
for k=6:46
if maxz==absz(k)
mz=k; %mz - max impedance index
k=46;
end
end
maximp=g(mz); %maximp - max impedance point (F5)
mimpa=angle(maximp);
mimpa=(180/pi)*mimpa; %mimpa - max impedance angle (F6)
y(10,w)=maxz;
y(11,w)=mimpa;
stang=angle(g(6));
stang=(180/pi)*stang; %stang - starting angle (F7)
endang=angle(g(46));
endang=(180/pi)*endang; %endang - ending angle (F8)
y(12,w)=stang;
y(13,w)=endang;
c=sqrt( ( (real(g(mz))-real(g(mz-1)) )^2) +((imag(g(mz))-imag(g(mz-1)))^2));
b=sqrt(((real(g(mz+1))-real(g(mz)))^2)+((imag(g(mz+1))-imag(g(mz)))^2));
a=sqrt(((real(g(mz+1))-real(g(mz-1)))^2)+((imag(g(mz+1))-imag(g(mz-1)))^2));
turnang=acos(((b^2)+(c^2)-(a^2))/(2*b*c));
turnang=(180/pi)*turnang;
% turnang - turning fase angle at the point of max impedance (F9)
y(14,w)=turnang;
L(1)=sqrt( ((real(g(6)))^2) +((imag(g(6)))^2));
for k=7:46
L(k)=sqrt( ( (real(g(k))-real(g(k-1)) )^2) +((imag(g(k))-imag(g(k-1)))^2));
end
L(47)=sqrt( ( (real(g(46)))^2) +((imag(g(46)))^2));
for k=1:mr
L1(k)=L(k);
end
mrlen=sum(L1); %mrlen - length up to the max resistance point (F10)
totlen=sum(L); %totlen - total length (F11)
y(15,w)=mrlen;
y(16,w)=totlen;
end;
|