«Интегрирование уравнений движения материальной точки, находящейся под действием переменных сил»
Задание: На наклонном участке АВ трубы на груз D, массой m действуют сила тяжести и сила сопротивления R, расстояние от точки А, где V=V0
, до точки В, равно L. На горизонтальном участке ВС на груз действует сила тяжести и переменная сила F = F(t).
Дано:
m = 4, кг
V0
= 12, м/с
Q = 12, Н
R = 0,8V2
, Н
L = 2.5, м
Fx
= -8cos(4t), Н
Определить:
Закон движения груза на участке ВС ( x = f(t) ).
Решение:
1. Пусть груз – материальная точка. Изобразим 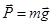 и и 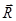 . Проведем ось Ax и составим дифференциальное уравнение в проекции на эту ось: . Проведем ось Ax и составим дифференциальное уравнение в проекции на эту ось:

Далее находим: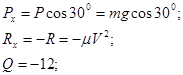
Учитывая, что Vx
= V:
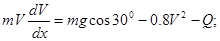 или или 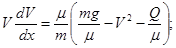
Выведем: 
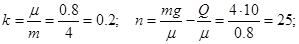
где g = 10 м/с.
Тогда:
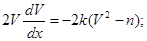
Разделяя переменные и интегрируя:
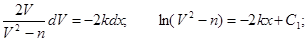
По Н.У. при x = 0: V = V0
, откуда:
 ; ;
Получим:
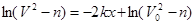 ; ;
Откуда:
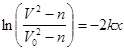 и и 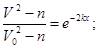
В результате: 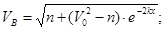
Полагая, что x=L=2.5 и заменяя k и n определим VB
:
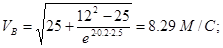
2. Рассмотрим движение на BC.
Рассмотрим движение ВС (V0
= V). Изобразим 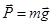 , , 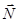 , и , и  . .
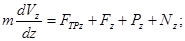 или или 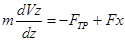 , где , где 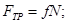
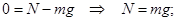

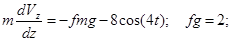
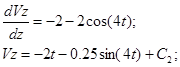
При t=0; V = V0
= VB
= 8.29 м/с:
С2
= VB
= 8.29 м/с.
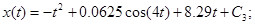
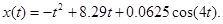

К-3 Вариант 18
 авр авр
   А А
    aA
Cv aA
Cv
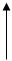 авр авр
  ac ac
 ацс ацс
  Eoa
aцс
C Eoa
aцс
C
aB
    Woa Woa
aB
 О В О В
  Y Y
 aB aB
X

Дано: ОА=10 АВ=10 АС=5 Woa
=2 EOA
=6
Найти: Ускорения во всех точках
Va=Woa*OA=20
Va=Wao*Acv=Wab*AB*sin45
Wab=Va/Cva=4/21/2
Vb=Wab*BCv=Wab*AB*cos45=20
Vc=Wab*CCv=21/2
2*BC/2ctg45=521/2
/2
aA
bp
= Eoa
*OA=60
aA
цс
=WOA
2
*OA=40
aB
цс
= WOA
2
*AB=80
aB=
aA
bp
+aA
цс
+aAB
ЦС
+aAB
bp
X: 21/2
/2*aB=
aA
цс
+aAB
BP
Y: 21/2
/2*aB=
aA
BP
+aAB
ЦС
aAB
BP
=========== ==MOI===\KOI0-U=140-40=100
EAB
=100/10=10
aB=
aA
вp
+aA
цс
+aAC
ЦС
+aAC
вp
aAC
вp
= EAB
*АВ=50
aAC
ЦС
= WAВ
2
*АС=40
X: 21/2
/2*ac=
aA
цс
+aAB
BP
Y: 21/2
/2*ac=
aA
BP
+aAB
ЦС
aC
=( acx
2
+acy
2
)1/2
«Определение скорости и ускорения точки по заданным уравнениям ее движения».
Задание: По заданным уравнениям движения точки М установить вид ее траектории и
для момента времени t = t1 (c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.
Исходные данные:
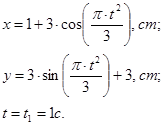
Решение:
Для нахождения траектории точки, возведем в квадрат и приравняем левые части уравнений движения, предварительно выделив из них cos и sin соответственно, в результате получим:
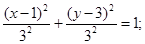 - траектория точки в координатной форме. - траектория точки в координатной форме.
Траектория представляет из себя окружность радиуса r=3 см.
Найдем проекции скорости и ускорения на оси координат дифференцируя по времени уравнения движения:
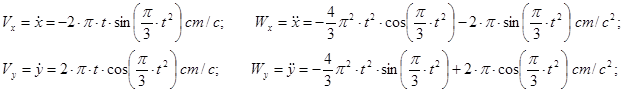
По найденным проекциям определяются модуль скорости и модуль ускорения точки:

Найдем модуль касательного ускорения точки по формуле: 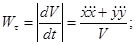
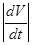 -выражает проекцию ускорения точки на направление ее скорости. Знак «+» при -выражает проекцию ускорения точки на направление ее скорости. Знак «+» при 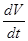 означает, что движение точки ускоренное, направления означает, что движение точки ускоренное, направления 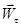 и и 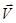 совпадают, знак «-» значит, что движение замедленное. совпадают, знак «-» значит, что движение замедленное.
Модуль нормального ускорения точки: 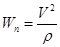 ; Т.к. радиус кривизны известен, но в качестве проверки применим другую формулу для нахождения модуля нормального ускорения: ; Т.к. радиус кривизны известен, но в качестве проверки применим другую формулу для нахождения модуля нормального ускорения: 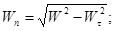
Когда найдено нормальное ускорение, радиус кривизны траектории в рассматриваемой точке определяется из выражения: 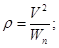
Результаты вычислений занесем в таблицу (для момента времени t = t1
= 1 c):
| Координаты (см) |
Скорость (см/с) |
Ускорение (см/с2
) |
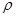 кривизны (см) кривизны (см) |
| x |
y |
Vx |
Vy |
V |
Wx |
Wy |
W |
Wτ |
Wn |
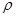 |
| 2.5 |
5.6 |
-5.4 |
3.2 |
6.3 |
-12 |
-8.3 |
14.6 |
5.5 |
13.5 |
2.922 |
Найденный радиус кривизны совпадает с определенным из уравнения траектории точки.
На рисунке показано положение точки М в заданный момент времени
Дополнительное задание. Определение скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения добавляется 3-е уравнение.
Исходные данные:
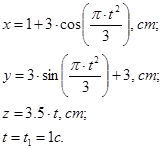
Решение:
Определим пространственную траекторию точки в координатной форме:
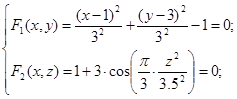 - траектория точки в координатной форме. - траектория точки в координатной форме.
Найдем проекции скорости и ускорения на оси координат дифференцируя по времени уравнения движения:

По найденным проекциям определяются модуль скорости и модуль ускорения точки:

Найдем модуль касательного ускорения точки по формуле: 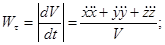
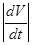 -выражает проекцию ускорения точки на направление ее скорости. Знак «+» при -выражает проекцию ускорения точки на направление ее скорости. Знак «+» при 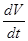 означает, что движение точки ускоренное, направления означает, что движение точки ускоренное, направления 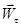 и и 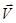 совпадают, знак «-» значит, что движение замедленное. совпадают, знак «-» значит, что движение замедленное.
Модуль нормального ускорения точки: 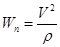 ; Т.к. радиус кривизны не известен, применим другую формулу для нахождения модуля нормального ускорения: ; Т.к. радиус кривизны не известен, применим другую формулу для нахождения модуля нормального ускорения:
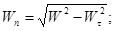
Когда найдено нормальное ускорение, радиус кривизны траектории в рассматриваемой точке определяется из выражения: 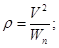
Результаты вычислений занесем в таблицу (для момента времени t = t1
= 1 c):
| Координаты (см) |
Скорость (см/с) |
Ускорение (см/с2
) |
кривизны (см) |
| x |
y |
z |
Vx |
Vy |
Vz |
V |
Wx |
Wy |
Wz |
W |
Wτ |
Wn |
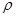 |
| 2.5 |
5.6 |
3.5 |
-5.4 |
3.2 |
3.5 |
7.2 |
-12 |
-8.3 |
0 |
14.6 |
5.3 |
15.5 |
3.6 |
«Определение реакций опор твердого тела».
Задание: Найти реакции опор конструкции.
Дано:
Q = 6, кН
G = 2, кН
a = 60, см
b = 40, см
c = 60, см
Определить:
Реакции опор конструкции.
Решение:
К раме ABCD приложены сила тяжести 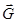 , сила , сила 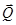 , реакция , реакция  стержня DC и реакции опор A и B. Реакция шарового шарнира А определяется тремя составляющими: стержня DC и реакции опор A и B. Реакция шарового шарнира А определяется тремя составляющими: 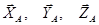 , а реакция петли В двумя: , а реакция петли В двумя: 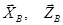 . .
Из этих сил – шесть неизвестных. Для их определения можно составить 6 уравнений равновесия.
Уравнения моментов сил относительно координатных осей:
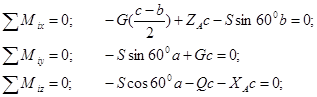
Уравнения проекций сил на оси координат:
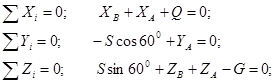
Из этих уравнений находим: решая уравнения, находим неизвестные реакции.
Результаты вычислений заносим в таблицу:
| Силы, кН |
| S |
XA
|
YA
|
ZA
|
XB
|
ZB
|
| 1.15 |
-6.57 |
0.57 |
-1 |
-12.57 |
2 |
Проверка:

Проверка показала, что реакции опор твердого тела найдены правильно.

В 18. Д – 1.
Дано: VA
= 0, a = 30°, f = 0,1, ℓ = 2 м, d = 3 м. Найти: h и t.
Решение: Рассмотрим движение камня на участке АВ. На него действуют силы тяжести G, нормальная реакция N и сила трения F.Составляем дифференциальное уравнение движения в проекции на ось X1
:  = G×sina - F , (F = f×N = fG×cosa) Þ = G×sina - F , (F = f×N = fG×cosa) Þ = g×sina - fg×cosa, = g×sina - fg×cosa,
Дважды интегрируя уравнение, получаем:
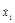 = g×(sina - f×cosa)×t + C1
, x1
= g×(sina - f×cosa)×t2
/2 + C1
t + C2
, = g×(sina - f×cosa)×t + C1
, x1
= g×(sina - f×cosa)×t2
/2 + C1
t + C2
,
По начальным условиям (при t = 0 x10
= 0 и 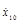 = VA
= 0) находим С1
и С2
: C1
= 0 , C2
= 0, = VA
= 0) находим С1
и С2
: C1
= 0 , C2
= 0,
Для определения VB
и t используем условия: в т.B (при t = t) , x1
= ℓ , 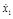 = VB
. Решая систему уравнений находим: = VB
. Решая систему уравнений находим:
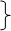 x1
= ℓ = g×(sina - f×cosa)×t2
/2 Þ 2 = 9,81×(sin30° - 0,1×cos30°)×t2
/2 , Þt = 0,99 c , x1
= ℓ = g×(sina - f×cosa)×t2
/2 Þ 2 = 9,81×(sin30° - 0,1×cos30°)×t2
/2 , Þt = 0,99 c ,
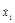 = VB
= g×(sina - f×cosa)×t VB
= 9,81×(sin30° - 0,1×cos30°)×0,99 = 4,03 м/с , = VB
= g×(sina - f×cosa)×t VB
= 9,81×(sin30° - 0,1×cos30°)×0,99 = 4,03 м/с ,
Рассмотрим движение камня на участке ВС.На него действует только сила тяжести G. Составляем дифференциальные уравнения движения
в проекции на оси X , Y : 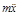 = 0 , = 0 , 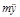 = G , = G ,
Дважды интегрируем уравнения: 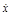 = С3
, = С3
,  = gt + C4
, = gt + C4
,
x = C3
t + C5
, y = gt2
/2 + C4
t + C6
,
Для определения С3
, C4
, C5
, C6
, используем начальные условия (при t = 0): x0
= 0 , y0
= 0 , 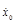 = VB
×cosa , = VB
×cosa , 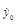 = VB
×sina , = VB
×sina ,
Отсюда находим : 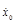 = С3
, ÞC3
= VB
×cosa , = С3
, ÞC3
= VB
×cosa , 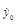 = C4
, ÞC4
= VB
×sina = C4
, ÞC4
= VB
×sina
x0
= C5
, ÞC5
= 0 , y0
= C6
, ÞC6
= 0
Получаем уравнения : 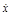 = VB
×cosa , = VB
×cosa ,  = gt + VB
×sina = gt + VB
×sina
x = VB
×cosa×t , y = gt2
/2 + VB
×sina×t
Исключаем параметр t : y = gx2
+ x×tga ,
2V2
B
×cos2
a
В точке С x = d = 3 м , у = h. Подставляя в уравнение VB
и d , находим h: h = 9,81×32
+ 3×tg30° = 5,36 м ,
2×4,032
×cos2
30°
|