БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
кафедра РЭС
реферат на тему:
«Линейные блоковые коды»
МИНСК, 2009
Линейным блоковым (n,k) - кодом называется множество N последовательностей длины n над GF(q), называемых кодовыми словами, которое характеризуется тем, что сумма двух кодовых слов является кодовым словом, а произведение любого кодового слова на элемент поля также является кодовым словом.
Обычно N=qk
, где k - некоторое целое число. Если q=2, линейные коды называются групповыми, так как кодовые слова образуют математическую структуру, называемую группой. При формирование этого кода линейной операцией является суммирование по mod2.
Способы задания линейных кодов
1. Перечислением кодовых слов, т.е. составлении списка всех кодовых слов кода.
Пример. В таблице 1 представлены все кодовые слова (5,3) - кода (ai
- информационные, а bi
- проверочные символы).
| Таблица 1 |
№ |
a1
|
a2
|
a3
|
b1
|
b2
|
| 1 |
0 |
0 |
1 |
1 |
0 |
| 2 |
0 |
1 |
0 |
1 |
1 |
| 3 |
0 |
1 |
1 |
0 |
1 |
| 4 |
1 |
0 |
0 |
0 |
1 |
| 5 |
1 |
0 |
1 |
1 |
1 |
| 6 |
1 |
1 |
0 |
1 |
0 |
| 7 |
1 |
1 |
1 |
0 |
0 |
| 8 |
0 |
0 |
0 |
0 |
0 |
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:
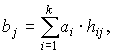
где
j - номер проверочного символа;
i - номер информационного символа;
hij
- коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
b1
= a2
+ a3
;
b2
= a1
+ a2
.
3. Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF(2) включает в себя 2n
векторов (n-последовательностей), а подпространством его является множество из 2k
кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n,k) - код полностью определяется набором из k кодовых слов, принадлежащих этому коду. Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) - код, который был представлен в таблице 1, может быть задан матрицей
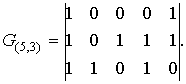
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением
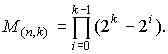
Для исключения неоднозначности в записи G(n,k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид

где
Ik
- единичная матрица, содержащая информационные символы;
Rk,r
- прямоугольная матрица, составленная из проверочных символов.
Пример. Порождающая матрица в систематическом виде для (5,3) - кода

Порождающая матрица G(n,k)
в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид

где Ir
- единичная матрица; - прямоугольная матрица в транспонированном виде матрицы Rk,r
из порождающей матрицы. - прямоугольная матрица в транспонированном виде матрицы Rk,r
из порождающей матрицы.
Пример. Проверочная матрица (5,3) - кода
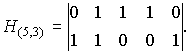
Основные свойства линейных кодов
1. Произведение любого кодового слова на транспонированную проверочную матрицу дает нулевой вектор размерности (n-k) на транспонированную проверочную матрицу дает нулевой вектор размерности (n-k)
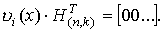
Пример. для кода (5,3)

2. Произведение некоторого кодового слова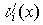 , т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается Si
(x) , т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается Si
(x)
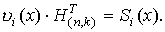
3. Между порождающей и проверочной матрицами в систематическом виде существует однозначное соответствие, а именно:
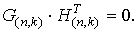
4. Кодовое расстояние d0
(n,k) - кода равно минимальному числу линейно зависимых столбцов проверочной матрицы
Пример.
для кода (5,3):
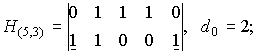
для кода (5,2):

5. Произведение информационного слова на порождающую матрицу дает кодовое слово кода
Пример. для кода (5,3)
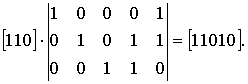
6. Два кода называются эквивалентными, если их порождающие матрицы отличаются перестановкой координат, т.е. порождающие матрицы получаются одна за другой перестановкой столбцов и элементарных операций над строками.
7. Кодовое расстояние любого линейного (n,k) - кода удовлетворяет неравенству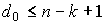 (граница Сингтона). Линейный (n,k) - код, удовлетворяющий равенству (граница Сингтона). Линейный (n,k) - код, удовлетворяющий равенству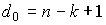 , называется кодом с максимальным расстоянием. , называется кодом с максимальным расстоянием.
Стандартное расположение группового кода
Стандартное расположение группового кода представляет разложение множества всех возможных n-элементных слов, представляющих собой группу, на смежные классы по подгруппе из 2k
кодовых слов, составляющих (n,k)-код (см. таблицу 2).
Образующие или лидеры смежных классов выбираются таким образом, чтобы в их состав вошли наиболее вероятные образцы ошибок в кодовом слове, т.е. образцы ошибок с наименьшим весом.
Пример. Код (5,3) имеет матрицы
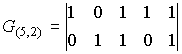 и и 
а стандартное расположение имеет вид,
| 00000 |
10111 |
01101 |
11010 |
| 00001 |
10110 |
01100 |
11011 |
| 00010 |
10101 |
01111 |
11000 |
| 00100 |
10011 |
01001 |
11110 |
| 01000 |
11111 |
00101 |
10010 |
| 10000 |
00111 |
11101 |
01010 |
| 00011 |
10100 |
01110 |
11001 |
| 10001 |
00110 |
11100 |
01011 |
Этот код имеет d0
=3. Он гарантирует исправление одиночных ошибок, конфигурация которых дана в первом столбце.
Процедура исправления ошибок следующая. Принятое кодовое слово анализируют и определяют, в каком столбце оно находится, а затем в качестве исправленного кодового слова берут слово, находящееся в верхней строке.
Однако, если длина кода большая и таблица стандартного расположения также значительная, пользоваться таким алгоритмом неудобно. Поэтому при декодировании используют таблицу синдромов (декодирования), представляющую собой список образцов ошибок (см. первый столбец стандартного расположения) и список соответствующих синдромов, которые однозначно характеризуют каждый смежный класс.
Коды Хэмминга
Кодом Хэмминга называется (n,k)-код, проверочная матрица которого имеет r = n-k строк и 2r
-1 столбцов, причем столбцами являются все различные ненулевые последовательности.
Пример. Для (7,4)-кода Хэмминга
 или или 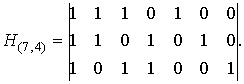
Проверочная матрица любого кода Хэмминга всегда содержит минимум три линейно зависимых столбца, поэтому кодовое расстояние кода равно трем.
Если столбцы проверочной матрицы представляют упорядоченную запись десятичных чисел, т.е. 1,2,3... в двоичной форме, то вычисленный синдром
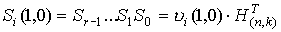
однозначно указывает на номер позиции искаженного символа.
Пример. Для (7,4)-кода Хэмминга проверочная матрица в упорядоченном виде имеет вид
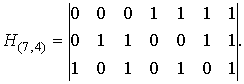
Пусть переданное кодовое слово  ,а принятое слово - ,а принятое слово -  . .
Синдром, соответствующий принятому слову будет равен
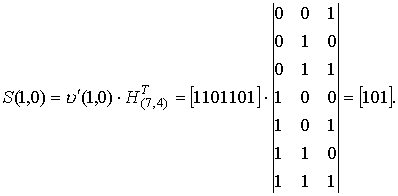
Вычисленный синдром указывает на ошибку в пятой позиции.
Проверочная матрица в упорядоченном виде представляет совокупность проверочных уравнений, в которых проверочные символы занимают позиции с номерами 2i
(i=0,1,2...).
Для (7,4)-кода Хэмминга проверочными уравнениями будут
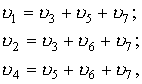
где 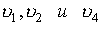 - проверочные символы. - проверочные символы.
Элементы синдрома определяются из выражений

Корректирующая способность кода Хэмминга может быть увеличена введением дополнительной проверки на четность. В этом случае проверочная матрица для рассмотренного (7,4)-кода будет иметь вид
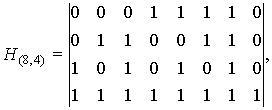 а кодовое расстояние кода d0
=4. а кодовое расстояние кода d0
=4.
Проверочные уравнения используются для построения кодера, а синдромные - декодера кода Хэмминга.
ЛИТЕРАТУРА
1. Лидовский В.И. Теория информации. - М., «Высшая школа», 2002г. – 120с.
2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И.Нефедов, В.И.Халкин, Е.В.Федоров и др. – М.: Высшая школа, 2001 г. – 383с.
3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.
4. Зюко А.Г. , Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г. –368 с.
5. Б. Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003 г. – 1104 с.
|