БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра РТС
РЕФЕРАТ
На тему:
"Метод статистической и гармонической линеаризации. Расчет автоколебаний по критерию Найквиста"
МИНСК, 2008
Метод основан на замене нелинейного преобразования процессов статистически эквивалентными им линейным преобразованиями. Нелинейный элемент заменяется линейным эквивалентом (рис.1). В результате замены система линеаризуется, что позволяет использовать методы исследования линейных систем.
Замена нелинейного преобразования линейным является приближенной и справедливой лишь в некоторых отношениях. Поэтому не существует однозначной эквивалентности при использовании различных критериев.
В частности, если нелинейность определяется безинерционной зависимостью вида
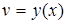 , (1) , (1)
используется два критерия эквивалентности.
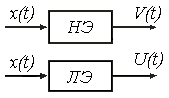
Рис.1.
Первый критерий предполагает равенство на выходе нелинейного элемента и его линейного эквивалента математических ожиданий и дисперсий процессов.
Второй критерий – минимум среднего квадрата разности процессов на выходе нелинейного элемента и его линейного эквивалента.
Процесс на входе и выходе нелинейного элемента представим в виде:
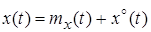 ; (2) ; (2)
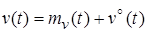 , (3) , (3)
где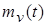 ─ математическое ожидание процесса на выходе НЭ; ─ математическое ожидание процесса на выходе НЭ;
 ─ центрированная случайная составляющая. ─ центрированная случайная составляющая.
Процесс на выходе линейного эквивалента представляется в следующем виде:
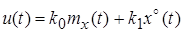 , (4) , (4)
где 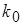 ─ коэффициент передачи линейного эквивалента по математическому ожиданию; ─ коэффициент передачи линейного эквивалента по математическому ожиданию; 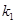 ─ коэффициент передачи по центрированной случайной составляющей. ─ коэффициент передачи по центрированной случайной составляющей.
Воспользуемся первым критерием эквивалентности:
 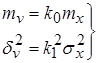 . (5) . (5)
Из этих уравнений находим
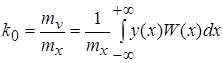 ; ;
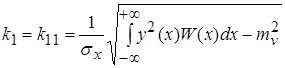 , ,
где 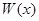 ─ плотность вероятности процесса на входе нелинейного элемента. ─ плотность вероятности процесса на входе нелинейного элемента.
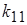 - коэффициент передачи линейного эквивалента по центрированной случайной составляющей (по первому критерию). - коэффициент передачи линейного эквивалента по центрированной случайной составляющей (по первому критерию).
По второму критерию эквивалентности:
 ; ;
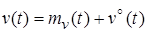 ; ;
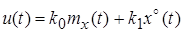 ; ;
 ; ;
Для определения 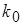 и и 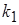 , при которых выполняется условие эквивалентности, найдем частные производные и приравняем их нулю: , при которых выполняется условие эквивалентности, найдем частные производные и приравняем их нулю:
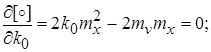 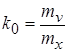 ; ;
 ; ;  ; ; 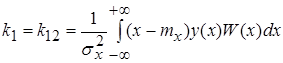 . .
При расчете этих коэффициентов полагают, что распределение на входе нормальное:
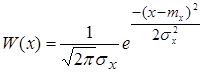 ; ;
Определив величины
 ; ;  . .
для типовых нелинейностей, заменяют последние коэффициентами передачи линейного эквивалента и анализируют систему линейными методами.
Для основных типов нелинейностей и нормальном распределении входного процесса коэффициенты рассчитаны и представлены в виде табличных значений. В частности, для характеристики релейного типа (рис.2)

Рис.2. Характеристика релейного типа:
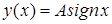 ; ; 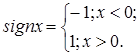
коэффициенты равны:
 ; ; 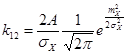 ; ; 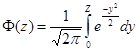 ; ;
Метод гармонической линеаризации
Основы метода.
Метод используется для исследования нелинейных систем, описываемых дифференциальными уравнениями различного порядка. Эффективен для расчета параметров собственных колебаний в системе, используется также для анализа точности при гармоническом задающем воздействии.
Рассмотрим метод применительно к расчету параметров собственных колебаний в нелинейной системе.
Разделим систему на линейную часть и нелинейное звено (рис.3).
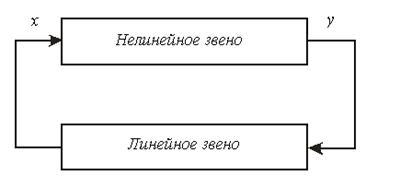
Рис.3. Модель нелинейной системы.
Уравнение линейной части:
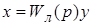 ,(6) ,(6)
При возникновении автоколебаний процесс 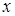 на выходе линейной части не является строго гармоническим, но мы будем полагать, что линейное звено является фильтром нижних частот и подавляет все гармоники, за исключением первой. Это предположение называется гипотезой фильтра. Если она не подтверждается, то ошибки при применении гармонической линеаризации могут быть значительными. на выходе линейной части не является строго гармоническим, но мы будем полагать, что линейное звено является фильтром нижних частот и подавляет все гармоники, за исключением первой. Это предположение называется гипотезой фильтра. Если она не подтверждается, то ошибки при применении гармонической линеаризации могут быть значительными.
 . .
Пусть
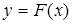 ; ;  . (7) . (7)
Представим  в виде ряда Фурье: в виде ряда Фурье:
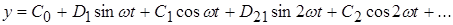 ; (8) ; (8)
Полагаем, что
 . .
Это справедливо, если  симметрична относительно начала координат и отсутствует внешнее воздействие. Полагая, что высшие гармоники подавляются, будем искать только симметрична относительно начала координат и отсутствует внешнее воздействие. Полагая, что высшие гармоники подавляются, будем искать только 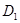 и и 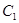
Из уравнения (7) находим:
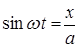 ; ; 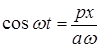 . (9) . (9)
Подставив (8. 20) в (8. 19) и ограничив ряд слагаемыми первой гармоники, получим:
 (10) (10)
где
 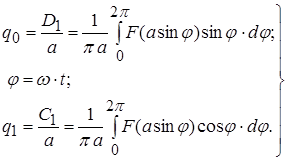 (11) (11)
Таким образом, нелинейное уравнение для  заменили приближенным линейным уравнением (11) для первой гармоники. заменили приближенным линейным уравнением (11) для первой гармоники.
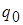 и и  называют гармоническими коэффициентами передачи нелинейного звена. Коэффициенты называют гармоническими коэффициентами передачи нелинейного звена. Коэффициенты 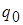 и и  в рассматриваемом случае зависят от амплитуды, при более сложной нелинейной зависимости зависят еще и от частоты. в рассматриваемом случае зависят от амплитуды, при более сложной нелинейной зависимости зависят еще и от частоты.
Рассчитанные значения коэффициентов гармонической линеаризации для типовых нелинейностей можно найти в учебниках и справочной литературе.
Передаточная функция разомкнутой системы может быть представлена в следующем виде:
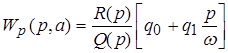 ; ; 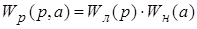 ; ;
где 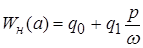 ─ эквивалентная передаточная функция нелинейно - го звена. ─ эквивалентная передаточная функция нелинейно - го звена.
Частотная передаточная функция разомкнутой системы
 . .
Характеристическое уравнение
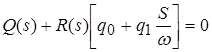 . .
Модуль частотной передаточной функции нелинейного звена
 . .
Фазочастотная характеристика
 ; ( ; (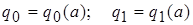 ) )
Модуль определяет отношение амплитуд, а  фазовый сдвиг на выходе относительно входного сигнала. фазовый сдвиг на выходе относительно входного сигнала.
Если  симметрична относительно начала координат, однозначна и не имеет гистерезиса, то симметрична относительно начала координат, однозначна и не имеет гистерезиса, то 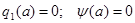 и тогда и тогда
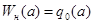 . .
Часто при анализе используется величина обратная  . Она называется гармоническим импедансом нелинейного звена: . Она называется гармоническим импедансом нелинейного звена:
 . .
Расчет автоколебаний по критерию Найквиста
В соответствии с критерием Найквиста строится годограф частотной передаточной функции разомкнутой системы
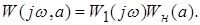
Условием возникновения в системе колебаний является прохождение амплитудно-фазовой характеристики через точку (-1,j0) комплексной плоскости. Для определения условий прохождения годографа через эту точку приравняем
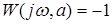 . .
Чтобы решить это уравнение можно, задавая значение амплитуды, строить амплитудно-фазовую характеристику(рис.8.18) Значение амплитуды а=А, при которой АФХ пройдет через точку (-1,j0) будет соответствовать амплитуде собственных колебаний. Значение частоты определяют по частоте в точке (-1,j0).

Рис.4. Амплитудно-фазовая характеристика нелинейной системы.
Тогда искомое колебание
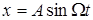 . .
При нелинейной зависимости вида 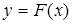 передаточную функцию разомкнутой системы можно представить в виде передаточную функцию разомкнутой системы можно представить в виде
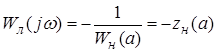 . (12) . (12)
Это уравнение решается графическим методом (рис.5). Строим амплитудно-фазовую характеристику линейного звена и кривую импеданса нелинейного звена. Определяем точку пересечения. Частоту 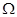 определим по АФХ линейного звена в точке пересечения. Амплитуду А определим по кривой импеданса нелинейного звена. определим по АФХ линейного звена в точке пересечения. Амплитуду А определим по кривой импеданса нелинейного звена.
Чтобы определить являются ли колебания устойчивыми автоколебаниями, нужно задать приращение амплитуды 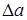 ; при этом точка на импедансе смещается влево вниз. Это будет соответствовать уменьшению ; при этом точка на импедансе смещается влево вниз. Это будет соответствовать уменьшению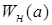 , следовательно, кривая годографа ПФ разомкнутой системы не будет охватывать точку с координатами , следовательно, кривая годографа ПФ разомкнутой системы не будет охватывать точку с координатами 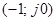 . Поэтому амплитуда колебаний начнет уменьшаться, и система вернется в исходное состояние. То же будет и при отрицательном приращении. . Поэтому амплитуда колебаний начнет уменьшаться, и система вернется в исходное состояние. То же будет и при отрицательном приращении.
Критерий устойчивости периодического режима сводится к тому, чтобы часть кривой 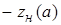 соответствующая меньшим амплитудам, охватывалась амплитудно-фазовой характеристикой линейной части. соответствующая меньшим амплитудам, охватывалась амплитудно-фазовой характеристикой линейной части.
При отсутствии в системе периодических режимов (решения уравнения (8.23)) можно предположить, что система будет устойчива.
Условие устойчивости равновесного состояния (отсутствия автоколебаний): при устойчивой или нейтральной в разомкнутом состоянии линейной части её АФХ не охватывает годограф 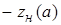 . .
ЛИТЕРАТУРА
1. Коновалов. Г.Ф. Радиоавтоматика: Учебник для вузов. – М.: Высш. шк., 2000.
2. Радиоавтоматика: Учеб. пособие для вузов. / Под ред. А. Бесекерского. - М.: Высш. шк., 2005.
3. Первачев С.В. Радиоавтоматика: Учебник для вузов. - М.: Радио и связь, 2002.
4. Цифровые системы фазовой синхронизации Под ред. И. Жодзишского – М.: Радио, 2000.
|