Статья: Причина периодичности Периодического закона

ПРИЧИНА ПЕРИОДИЧНОСТИ ПЕРИОДИЧЕСКОГО ЗАКОНА

Клюйков Р.С., Клюйков С.Ф.

Первоначально схема построения конфигурации электронной составляющей атомов не выводилась из каких-либо строгих теоретических (тем более - математических) представлений. Она просто основывалась на наблюдаемых изменениях химических свойств и спектров элементов.

Первое физическое обоснование схема получила лишь методами квантовой механики Н.Бора. Появились представления о внешних электронных оболочках, уровнях, подуровнях, о их периодической повторяемости, которыми обуславливалось периодическое изменение химических свойств элементов. Была найдена физическая причина периодичности Периодического закона.

Многообразие современных моделей строения атомов всё ещё основывается на главном постулате Н.Бора: в атоме существует чёткая последовательность вложенных друг в друга сферических электронных оболочек. Однако этим принципом просто рассматривается сформированная Природой последовательность, не объясняется механизм формирования, не показываются закономерности, использованные Природой.

Последовательность заполнения электронных уровней хорошо описывается мнемоническим правилом В.М.Клечковского. Но, опять же – не определяется им. Исследователи отмечают «размывания периодичности», явные нарушения диктуемых этим правилом чётких границ заполняемых подуровней, начиная с шестого периода. Выпускается из виду большая группа элементов (формально – подчиняющихся правилу, но в действительности – более тонко размывающих периодичность): 24Cr, 29Cu, 41Nb, 42Mo, 44Ru, 45Rh, 46Pd, 47Ag, 78Pt, 79Au, 111Rg.

Строгое количественное объяснение периодичности изменения химических и физических свойств элементов оказалось чрезвычайно сложной задачей. По сей день отсутствует математическая причина периодичности Периодического закона.

Идеальная математика[1-3] обобщает порядки, по которым складывалось всё в Природе. Самый простой порядок – сложение натуральных чисел (1я ступень), затем – умножение целых чисел (2я ступень), и т.д.

Рассмотрим, как Природа использовала эти порядки на примере создания ею химических элементов.

Вначале напомним основные физические условия такого создания.

Согласно Периодическому закону Д.И.Менделеева, элементы усложнялись добавлением одного протона в ядро и одного электрона в оболочку каждого атома. Сосредоточим внимание только на строительстве электронных оболочек.

Электроны в оболочке располагаются уровнями, на которых их энергии очень близки. Энергия электрона определяется его четырьмя квантовыми числами:

n - главное (адрес уровней): 1,2,3,4,5,6,7;

l - вспомогательное (адрес подуровней s,p,d,f): 0,1,2,3;

m - магнитное (адрес орбитали): целые числа от –l до +l;

s - спиновое (спин): +1/2, -1/2.

Согласно принципу Паули в атоме не должно быть двух электронов в одинаковом состоянии. Поэтому «добавленные» электроны должны отличаться разными комбинациями их квантовых чисел. При создании нового элемента изменения всех переменных должны быть минимальными!!!

Соблюдая эти физические условия, Природа создала все химические элементы следующими минимальными усложнениями их электронных оболочек. В обозначении электронных формул опустим уже сформированные подуровни и оставим только последние, ещё формируемые (в круглых скобках – нормальная форма оболочки, об этом - ниже).

1H 1s¹ .

2He 1s² .

3Li 2s¹ .

4Be 2s² .

5B 2s² 2p¹ .

6C 2s² 2p² .

7N 2s² 2p³ .

8O 2s² 2p⁴ .

9F 2s² 2p⁵ .

10Ne 2s² 2p⁶ .

11Na 3s¹ .

12Ma 3s² .

13Al 3s² 3p¹ .

14Si 3s² 3p² .

15P 3s² 3p³ .

16S 3s² 3p⁴ .

17Cl 3s² 3p⁵ .

18Ar 3s² 3p⁶ .

19K 4s¹ .

20Ca 4s² .

21Sc 4s² 3d¹ .

22Ti 4s² 3d²

23V 4s² 3d³

24Cr (4s² 3d⁴ ) 4s¹ 3d⁵

25Mn 4s² 3d⁵

26Fe 4s² 3d⁶

27Co 4s² 3d⁷

28Ni 4s² 3d⁸ .

29Cu (4s² 3d⁹ ) 4s¹ 3d¹⁰ .

30Zn 4s² 3d¹⁰ .

31Ga 4s² 4p¹ .

32Ge 4s² 4p² .

33As 4s² 4p³ .

34Se 4s² 4p⁴ .

35Br 4s² 4p⁵ .

36Kr 4s² 4p⁶ .

37Rb 5s¹ .

38Sr 5s² .

39Y 5s² 4d¹ .

40Zr 5s² 4d² .

41Nb (5s² 4d³ ) 5s¹ 4d⁴ .

42Mo (5s² 4d⁴ ) 5s¹ 4d⁵ .

43Tc 5s² 4d⁵ .

44Ru (5s² 4d⁶ ) 5s¹ 4d⁷ .

45Rh (5s² 4d⁷ ) 5s¹ 4d⁸ .

46Pd (5s² 4d⁸ ) 5s⁰ 4d¹⁰ .

47Ag (5s² 4d⁹ ) 5s¹ 4d¹⁰ .

48Cd 5s² 4d¹⁰ .

49In 5s² 5p¹ .

50Sn 5s² 5p² .

51Sb 5s² 5p³ .

52Te 5s² 5p⁴ .

53J 5s² 4p⁵ .

54Xe 5s² 5p⁶ .

55Cs 6s¹ .

56Ba 6s² .

57La (6s² 4f¹ ) 6s² 5d¹ .

58Ce (6s² 4f² ) 6s² 5d¹ 4f¹ .

59Pr 6s² 4f³ .

60Nd 6s² 4f⁴ .

61Pm 6s² 4f⁵ .

62Sm 6s² 4f⁶ .

63Eu 6s² 4f⁷ .

64Gd (6s² 4f⁸ ) 6s² 5d¹ 4f⁷ .

65Tb 6s² 4f⁹ .

66Dy 6s² 4f¹⁰ .

67Ho 6s² 4f¹¹ .

68Er 6s² 4f¹² .

69Tu 6s² 4f¹³ .

70Yb 6s² 4f¹⁴ .

71Lu 6s² 5d¹ .

72Hf 6s² 5d² .

73Ta 6s² 5d³ .

74W 6s² 5d⁴ .

75Re 6s² 5d⁵ .

76Os 6s² 5d⁶ .

77Ir 6s² 5d⁷ .

78Pt (6s² 5d⁸ ) 6s¹ 5d⁹ .

79Au (6s² 5d⁹ ) 6s¹ 5d¹⁰ .

80Hg 6s² 5d¹⁰ .

81Tl 6s² 6p¹ .

82Pb 6s² 6p² .

83Bi 6s² 6p³ .

84Po 6s² 6p⁴ .

85At 6s² 6p⁵ .

86Rn 6s² 6p⁶ .

87Fr 7s¹ .

88Ra 7s² .

89Ac (7s² 5f¹ )7s² 6d¹ .

90Th (7s² 5f² ) 7s² 6d² .

91Pa (7s² 5f³ ) 7s² 6d¹ 5f² , 7s² 6d² 5f¹ .

92U (7s² 5f⁴ ) 7s² 6d¹ 5f³ .

93Np 7s₂ 5f⁵ .

94Np 7s₂ 5f⁶ .

95Np 7s₂ 5f⁷ .

96Cm (7s₂ 5f⁸ ) 7s² 6d¹ 5f⁷ .

97Bk 7s₂ 5f⁹ .

98Cf 7s₂ 5f¹⁰ .

99Es 7s₂ 5f¹¹ .

100Fm 7s₂ 5f¹² .

101Md 7s₂ 5f¹³ .

102No 7s₂ 5f¹⁴ .

103Lr 7s₂ 6d¹ .

104Rf 7s₂ 6d² .

105Db 7s₂ 6d³ .

106Sg 7s₂ 6d⁴ .

107Bh 7s₂ 6d⁵ .

108Hs 7s₂ 6d⁶ .

109Mt 7s₂ 6d⁷ .

110Ds 7s₂ 6d⁸ .

111Rg (7s² 6d⁹ )7s¹ 6d¹⁰ .

112Cp 7s₂ 6d¹⁰ .

113Uut 7s² 7p¹ .

114Ku 7s² 7p² .

115Uup 7s² 7p³ .

116Uuh 7s² 7p⁴ .

117Uus 7s² 7p⁵ .

118Uuo 7s² 7p⁶ .

Проанализируем особенности усложнения строения электронных оболочек. Несмотря на исключения логической последовательности усложнения электронных формул, «исправляемые» однако содержимым в скобках (об этом - ниже), соблюдается следующая закономерность.

Вначале самым простым порядком Идеальной математики - сложением 1й ступени (прибавлением единицы, где единицей служит «добавленный» электрон с определёнными значениями его квантовых чисел n,l,m,s - обозначим его a) создается 1H 1s¹ . Сложением 1й ступени Идеальной математики требуется «добавлять» следующий электрон, абсолютно подобный электрону a, но принцип Паули запрещает это. Поэтому возможности такого порядка усложнения электронных оболочек, жёстко ограниченные строгими физическими условиями, исчерпываются.

Переходим к более сложному порядку Идеальной математики – умножению 2й ступени. Самое простое из них – это умножение двух одинаковых целых чисел. В нашем случае – это образование орбитали из двух одинаковых электронов aa (не трёх, не четырёх…) и создание 2He 1s² . Для удовлетворения принципа Паули у двух электронов a с одинаковыми квантовыми числами n,l,m разные спины s. На этом комбинации самого простого умножения исчерпываются, и размеры пространства первого уровня – тоже. Так Природа построила все элементы первого периода.

Во втором периоде, используя минимальное усложнение - увеличение энергии переходом на второй уровень, опять строим: сложением - 3Li 2s¹ и умножением - 4Be 2s² . Размеры пространства второго уровня позволяют использовать для строительства следующий по сложности порядок Идеальной математики – сочетание 3й ступени (минимальное из возможных) «по два из трёх» (ab,ac,bc). То есть, в орбиталях второго уровня возможно добавление комбинаций сочетания по два из трёх электронов (обозначим их a,b,c), разнящихся своими квантовыми числами n,l,m,s. Всего комбинации нового порядка строительства электронных оболочек обеспечивают возможность присоединения ещё шести «добавленных» электронов. Поэтому таким порядком строятся следующие шесть элементов: 5B 2s² 2p¹ ; 6C 2s² 2p² ; 7N 2s² 2p³ ; 8O 2s² 2p⁴ ; 9F 2s² 2p⁵ ; 10Ne 2s² 2p⁶ . На этом возможности данного порядка, да и пространство второго уровня – исчерпываются. Так Природа построила все элементы второго периода.

При строительстве элементов третьего периода опять, используя минимальное усложнение - увеличение энергии, переходим на третий уровень, и уже на нём начинаем располагать новые «добавленные» электроны: опять сложением - 11Na 3s¹ ; умножением - 12Ma 3s² ; сочетанием - 13Al 3s² 3p¹ , 14Si 3s² 3p² , ... 18Ar 3s² 3p⁶ . Так Природа построила все элементы третьего периода.

Для строительства элементов четвёртого периода пространство третьего уровня позволяет располагать другие «добавленные» электроны, но минимальная энергия целого атома заставляет предварительно заполнить начало следующего, четвёртого уровня: опять сложением - 19K 4s¹ и умножением - 20Ca 4s² . И только после этого продолжается заполнение ранее недостроенного третьего уровня на подуровне 3d следующим по сложности порядком Идеальной математики – размещением 4й ступени, опять минимальным: «по два из трёх» (aa,ab,ac,bc,ba,ca,cb,bb,cc). Но на третьем уровне часть комбинаций такого размещения (aa,ab,ac,bc) уже использована для строительства подуровней 3s² (aa) и 3p⁶ (ab,ac,bc). Неиспользованными остаются только пять орбиталей для комбинаций (ba,ca,cb,bb,cc) – новый вклад, а их образуют десять «добавленных» электронов. Поэтому таким порядком строятся следующие десять элементов: 21Sc… 30Zn. При этом первые пять элементов от 21Sc 4s² 3d¹ до 25Mn 4s² 3d⁵ образуются по комбинациям (ba,ca и начало cb), зеркально повторяющим комбинации(ab,ac и начало bc) сочетания, по которым строились элементы от 5B до 9F и от 13Al до 17Cl. Поэтому элементы Sc-Mn попадают в аналогичные группы Периодической таблицы Д.И.Менделеева, но по «зеркальным» свойствам выделены голубым цветом. Далее, по комбинациям (конец cb и bb,cc), «зеркально» повторяющим комбинацию (aa), образуется особая группа d-переходных металлов 26Fe 4s² 3d⁶ , 27Co 4s² 3d⁷ , 28Ni 4s² 3d⁸ , а также 29Cu 4s¹ 3d¹⁰ (4s² 3d⁹ ) и 30Zn 4s² 3d¹⁰ – все тоже «зеркальные» (например, построенным по комбинации aa: 3Li 1s² 2s¹ и 4Be 1s² 2s² ) и потому «голубые».

Четвёртый период таблицы Д.И.Менделеева заканчивается заполнением подуровня 4p обычным сочетанием «по два из трёх» шести элементов: 31Ga 4s² 3d¹⁰ 4p¹ … 36Kr 4s² 3d¹⁰ 4p⁶ .

Теперь понятна повторяющаяся логика усложнения электронных оболочек очередных элементов пятого периода: от 37Rb 5s¹ до 54Xe 5s² 5p⁶ .

Начало шестого периода – тоже стандартно: сложением - 55Cs 6s¹ и умножением - 56Ba 6s² . Далее продолжает заполняться четвёртый уровень на подуровне 4f, перебором комбинаций теперь уже следующего порядка Идеальной математики с минимальным усложнением - размещением «по два из четырёх» электронов (обозначим их a,b,c,d), опять разнящихся своими квантовыми числами n,l,m,s. При этом всего возможных комбинаций должно быть (aa,ab,ac,bc,ba,ca,cb,bb,cc,ad,bd,cd,dd,da,db,dc). Но на четвёртом уровне, на подуровнях 4s² ,4p⁶ ,4d¹⁰ , уже заполнены комбинации (aa,ab,ac,bc,ba,ca,cb,bb,cc). Осталось заполнить только комбинации (ad,bd,cd,dd,da,db,dc), а в них – четырнадцать «добавляемых» электронов. Поэтому, таким порядком добавления электронов на подуровне 4f строятся следующие четырнадцать элементов: 57La…70Yb. Вот почему они «вывалились» в краткой и полудлинойформах Периодической таблицы (в таблице нет комбинаций, подобных им)в отдельную побочную подгруппу лантаноидов.

Остановимся на явлении «размывания периодичности».

Известно, что наибольшей устойчивостью обладают незаполненные (d⁰ ,f⁰ ), наполовину заполненные (d⁵ ,f⁷ ) и полностью заполненные (d¹⁰ ,f¹⁴ ) подуровни. Поэтому «добавляемому» электрону энергетически выгодно перейти на эти устойчивые или близкие к ним подуровни, нарушая, «размывая» периодичность. Поводом для перехода может служить малейшее возбуждение атома. И вариантов перехода может быть больше одного, например - 91Pa (7s² 5f³ ) 7s² 6d¹ 5f² , 7s² 6d² 5f¹ . Но этим сообщением подчёркивается, что в любом наблюдаемом случае «размывания периодичности» всегда имеется задуманная Природой единственная идеальная форма электронной оболочки атома (приведенная в круглых скобках), назовём её – нормальной. Ранее мы обошли вниманием примеры такого отклонения от нормы: уже пройденные 24Cr(4s² 3d⁴ )4s¹ 3d⁵ , 29Cu (4s² 3d⁹ ) 4s¹ 3d¹⁰ , 41Nb(5s² 4d³ ) 5s¹ 4d⁴ , 42Mo(5s² 4d⁴ ) 5s¹ 4d⁵ , 44Ru (5s² 4d⁶ ) 5s¹ 4d⁷ , 45Rh (5s² 4d⁷ ) 5s¹ 4d⁸ , 46Pd (5s² 4d⁸ ) 5s⁰ 4d¹⁰ , 47Ag (5s² 4d⁹ ) 5s¹ 4d¹⁰ и следующие далее 78Pt (6s² 5d⁸ ) 6s¹ 5d⁹ , 79Au (6s² 5d⁹ ) 6s¹ 5d¹⁰ , 111Rg(7s² 6d⁹ ) 7s¹ 6d¹⁰ , объединяемые в особую группу общим свойством – переходом «добавляемого» электрона с s-подуровня на более ближний, но более устойчивый вновь создаваемый d-подуровень.

Лантаноиды образуются заполнением 4f подуровня. В то же время совсем рядом расположен незаполненный 5d подуровень, а разница энергий между ними настолько мала, что при незначительном возбуждении один или даже два электрона легко переходят с 4f на 5d и становятся валентными.

Родоначальник группы - 57La (6s² 4f¹ )6s² 5d¹ – первый пример отклонения от нормы такого рода: его «добавляемый» (первый для 4f) электрон располагается на 5d¹ , ради создания более устойчивого 4f⁰ . Вместе со следующими далее: 58Ce (6s² 4f² )6s² 5d¹ 4f¹ , 64Gd (6s² 4f⁸ )6s² 5d¹ 4f⁷ , 89Ac (7s² 5f¹ )7s² 6d¹ , 90Th (7s² 5f² )7s² 6d² , 91Pa (7s² 5f³ )7s² 6d¹ 5f² ,7s² 6d² 5f¹ 92U (7s² 5f⁴ )7s² 6d¹ 5f³ , 96Cm (7s² 5f⁸ )7s² 6d¹ 5f⁷ - эти примеры «размывания периодичности» объединяются в другую особую группу общим свойством – переходом «добавляемого» электрона с f-подуровня на более дальний d-подуровень, ради более устойчивого оставляемого f-подуровня.

За этими исключениями опять следуют нормальные лантаноиды 59Tc 6s² 4f³ …63Eu 6s² 4f⁷ и 65Tb 6s² 4f⁹ …70Yb 6s² 4f¹⁴ .

Сам 57La (6s² 4f¹ )6s² 5d¹ справедливо будет поместить первым в верхнем ряду побочной группы, чтобы теперь все 14 лантаноидов (в их нормальной, невозбуждённой форме) были, наконец, вместе рядом, выстроенные по количеству «добавляемых» 4f электронов, от 4f¹ до 4f¹⁴ . Тогда 64Gd (6s² 4f⁸ )6s² 5d¹ 4f⁷ переместится с последнего в верхнем ряду на почётное для его особого статуса место - первое в нижнем ряду. При такой трансформации таблицы становится очевидной природа условного деления лантаноидов на два семейства: цериево – верхний ряд семи элементов 57La…63Eu, построенных по комбинациям (ad,bd,cd и начало dd); тербиево (чаще - иттриево) – нижний ряд семи элементов 64Gd…70Yb, построенных по комбинациям (da,db,dc и конец dd) . Многие свойства этих семейств «зеркально» изламываются на Gd, например: величины ионных радиусов; кристаллографические данные; тетрад-эффект устойчивости комплексных соединений и др. Причина «зеркальности» 4f подуровня подобна рассмотренной выше «зеркальности» 3d подуровня (сравните соответствующие комбинации).

Несмотря на устоявшееся мнение, что следующий элемент 71Lu 6s² 5d¹ тоже относится к лантаноидам и даже размещается вместе с ними (последним) в этой побочной группе, данным сообщением он доказательно исключается из неё. Но, благодаря своим свойствам, очень родственным лантаноидам, он заслуженно размещается в почётной клеточке таблицы, занимаемой прежде самим лантаном. Такое перемещение 71Lu будет справедливым по отношению к 21Sc 4s² 3d¹ и 39Y 5s² 4d¹ , с которыми лантаноиды образуют особую группу редкоземельных элементов (сравните их комбинации). Теперь все нелантаноиды (Sc,Y,Lu) среди редкоземельных элементов окажутся на таблице в равных условиях.

Далее, аналогично подуровням четвёртого и пятого периодов, в шестом периоде продолжают заполняться: подуровень 5d - размещением «по два из трёх» от 71Lu 6s² 5d¹ до 80Hg 6s² 5d¹⁰ , образуя особую группу d-переходных металлов Os,Ir,Pt, а также Au и Hg – все «голубые»; подуровень 6p – сочетанием «по два из трёх», образуя элементы от 81Tl 6s² 5p¹ до 86Em 6s² 6p⁶ . Так Природа построила все элементы шестого периода.

Аналогично шестому, усложняются элементы седьмого периода от 87Fr 7s¹ до 118Uuo 7s² 7p, только «ещё формируемые» подуровни возрастают на единицу.

Так, на подуровне 5f размещением «по два из четырёх» строятся очередные 14 элементов, вновь образующие отдельную побочную подгруппу – актиноидов.

У актиноидов различие энергетических состояний электронов подуровней 5f и 6d ещё меньше, чем у лантаноидов 4f и 5d. Поэтому «добавленные» электроны первых актиноидов легко переходят на 6d, становясь валентными, повышая общую валентность элемента вплоть до +6. Эта сверхлёгкая возбудимость актиноидов создаёт трудности точного установления их действительных электронных конфигураций. От Th до Am энергии заполняемых орбиталей подуровней 5f, 6d, 7s и 7p очень близки, они способны перекрываться, а энергии перехода электронов между ними лежат в пределах обычных химических связей. Но чётко установленная данным сообщением нормальная форма элементов (в круглых скобках) позволяет выстроить актиноиды по-новому.

Отдельная группа актиноидов должна начинаться с самого 89Ac (7s² 5f¹ )7s² 6d¹ . Далее идут: 90Th (7s² 5f² )7s² 6d² , 91Pa (7s² 5f³ )7s² 6d¹ 5f² ,7s² 6d² 5f¹ , 92U (7s² 5f⁴ )7s² 6d¹ 5f³ , 93Np 7s² 5f⁵ , 94Pu 7s² 5f⁶ , 95Am 7s² 5f⁷ – верхний ряд, построенный комбинациями (ad,bd,cd и начало dd); 96Cm (7s² 5f⁸ ) 7s² 6d¹ 5f⁷ , 97Bk 7s² 5f⁹ , 98Cf 7s² 5f¹⁰ , 99Es 7s² 5f¹¹ , 100Fm 7s² 5f¹² , 101Md 7s² 5f¹³ , 102No 7s² 5f¹⁴ – нижний ряд, построенный комбинациями (da,db,dc и конец dd). «Зеркальный» излом свойств актиноидов - на 96Cm (сравните соответствующие комбинации).

Бывший последним в побочной группе актиноидов 103Lr 7s² 6d¹ исключается из неё и помещается в клеточку Периодической таблицы, где был ранее 89Ac. С него начинает заполняться подуровень 6d размещением «по два из трёх» до 112Cp 7s₂ 6d¹⁰ , а потом - подуровень 7p сочетанием «по два из трёх» от 113Uut 7s² 7p¹ до 118Uuo 7s² 7p⁶ , аналогично шестому периоду.

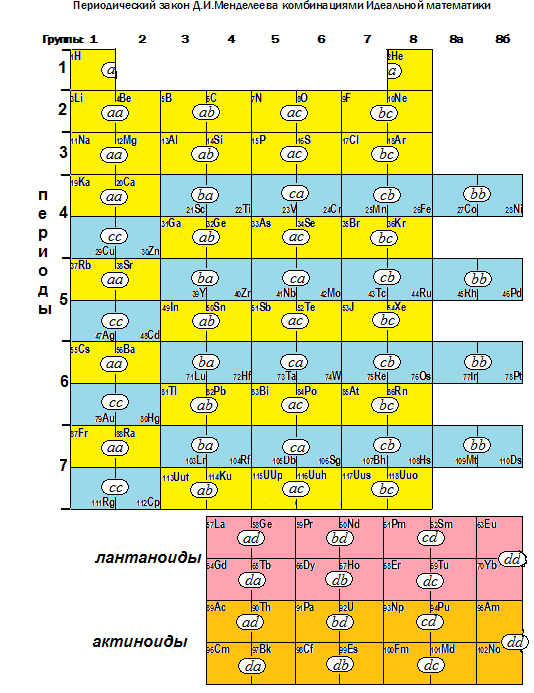
Таким образом, несмотря на отклонения отдельных элементов от задуманной Природой нормальной формы, кажущуюся непоследовательность из-за выполнения жёстких физических условий, наблюдается стабильное, чёткое соблюдение математических операций усложнения электронных оболочек химических элементов в строгой последовательности, начертанной Идеальной математикой:

сложением одной единицы

умножением двух чисел

сочетанием «по два из трёх» чисел

размещением «по два из трёх» чисел

размещением «по два из четырёх» чисел

a

aa

ab,ac,bc

aa,ab,ac,bc,ba,ca,cb,bb,cc

aa,ab,ac,bc,ba,ca,cb,bb,cc,ad,bd,cd,dd,da,db,dc

Чёткое соблюдение последовательности комбинаций математических операций повторялось на каждом следующем периоде (рисунок), неоднократно! Более того, каждая предыдущая операция всеми своими комбинациями постоянно вкладывалась во все последующие. Эта стабильность создала основу повторяемости, преемственности – последовательность комбинаций стала математической причиной периодичности Периодического закона Д.И.Менделеева! Благодаря выявленным комбинациям – периодичность становится очевидной, более наглядной. Именно она позволяет выстраивать таблицу элементов спиралями (следующий виток включает в себя весь опыт предыдущих витков и своё новое) и другими экзотическими пространственно расширяющимися формами.

Комбинаторика Природы ограничилась соединениями только «по два» - не в этом ли причина «двухкомнатных» орбиталей? И этих простейших математических порядков первых четырёх 1й-4й ступеней Идеальной математики хватило для сотворения всего многообразия химических элементов!

Уместен вопрос: есть ли граница натурального ряда химических элементов?

Можно отметить, что образование элементов комбинациями операций Идеальной математики шло следующими этапами.

1й этап. Образуется элемент 1H комбинацией сложения a. Повторением 1го этапа комбинацией умножения aa образуется 1й период.

2й этап. Образуются элементы 2го периода повторением комбинаций всего 1го периода с добавлением новых комбинаций сочетания «по два из трёх» (ab,ac,bc). Повторением комбинаций всего 2го этапа образуются элементы 3го периода.

3й этап. Образуются элементы 4го периода повторением комбинаций всего 2го этапа с добавлением новых комбинаций размещения «по два из трёх» (ba,ca,cb,bb,cc). Повторением комбинаций всего 3го этапа образуются элементы 5го периода.

4й этап. Образуются элементы 6го периода повторением комбинаций всего 3го этапа с добавлением новых комбинаций размещения «по два из четырёх» (ad,bd,cd,dd,da,db,dc). Повторением комбинаций всего 4го этапа образуются элементы 7го периода.

Будет ли следующий 5й этап … «с добавлением новых комбинаций размещения «по два из пяти»»? Или … «с добавлением новых комбинаций размещения «по три из четырёх»»? Очевидно – не будет, так как до сих пор каждое новое усложнение операции Природа повторяла только по два раза! Усложнение операции размещения уже повторилось дважды – предел! Как и завещал Д.И.Менделеев: «В десятом ряду (7м периоде) … есть повод заключить, что здесь мы уже близки к концу возможных форм элементарных соединений (комбинаторики? Авторы)».

Нужно новое усложнение математической операции образования элементов. Идеальная математика подсказывает, что это будет операция её 5й ступени – интегрирование функций.

То есть, следующие (после 118Uuo) усложнения химических элементов должны осуществляться уже не простым численным прибавлением очередных «добавленных» электронов соединениями комбинаторики – все возможные новые комбинации исчерпались! Необходимо организовывать «добавленные» электроны функциональными зависимостями. Новые электронные конфигурации должны выстраиваться определёнными функциональными зависимостями. Но как?

В Идеальной математике слагаемые (интегралы постоянной величины по переменной величине) функциональной зависимости чисел 5й ступени зародились ещё на 4й ступени. Поищем слагаемые усложнения химических элементов 5го этапа на уже пройденных этапах, они должны там проявляться.

Операцию 4й ступени размещение «по два из трёх» Природа впервые использовала в 4м периоде, начиная с 21Sc. И на этом элементе в «долине стабильности», области стабильных нуклонов, закончились лёгкие ядра с A/Z=1. Начиная с Z>20 нуклиды нестабильны к b-распаду в основном состоянии.

С 39Y началось повторное использование операции размещение «по два из трёх». И почти для всех ядер с А>90 выполняется условие возможности их спонтанного деления: потенциальная энергия делящегося ядра превышает сумму масс осколков деления.

С 57La началось использование операции размещение «по два из четырёх». И с этого места таблицы начинается протонная радиоактивность ядер в их основных состояниях.

С 89Ac началось повторное использование операции размещение «по два из четырёх». И отсюда же начинается естественная радиоактивность, нестабильность к a-распаду. 92U – последний из естественных элементов, найденных в Природе. Все более сложные – нестабильны, со всё уменьшающимся полупериодом распада, и давно превратились в более лёгкие, более стабильные элементы.

Таким образом, в формировании электронных оболочек химических элементов очевидна связь математической операции размещение с нестабильностью ядер этих элементов к различного родарадиоактивности, к превращениям элементов. То есть, искомым интегралом дальнейшего (после 118Uuo) усложнения химических элементов на 5м этапе является превращение, видоизменение ядер и их составляющих ядерными реакциями. Ядерные реакции и есть искомые функции 5й ступени Идеальной математики, по которым уже очень давно усложняется далее в Природе мир химических элементов, например – в телах звёзд. Следовательно:

5й этап. Образуются новые химические элементы функциональным складыванием ядерных превращений (ядерные реакции).

6й этап. Образуются новые состояния химических элементов складыванием взаимозависимых ядерных реакций (цепные реакции, мазеры, лазеры).

7й этап. Образуются новые континуумы химических элементов складыванием взаимовлияющих состояний (термоядерные реакции).

8й этап. Образуются новые уровни химических элементов складыванием взаимосвязанных континуумов (атомная бомба, водородная бомба, атомная энергетика).

9й этап. Образуются модели развития химических элементов складыванием их уровней единым направлением по возрастающим критериям (управляемый термоядерный синтез, ТОКАМАК СССР, токамаки других стран).

10й этап. Образуется модель вывода химических элементов складыванием различных их моделей развития единой стратегией по возрастающим приоритетам (международный проект ITER, квантовая телепортация, квантовые компьютеры). И так далее…

Просматривается чёткая дорога, вымощенная операциями Идеальной математики, которой ещё на заре Времён воспользовалась Природа, и по которой следом за ней неосознанно, начиная с Адама и Евы, идут химики и физики к Познанию, к новым открытиям и свершениям.

Не стоит зацикливаться на поиске мифически и магически «стабильных» (Z=126 и 164) элементов. Надо смириться с тем, что таблица Д.И.Менделеева закончилась на 118м элементе, и максимум энергии направить на дальнейшее осознанное совершенствование химии и физики новыми (10й, 11й и т.д.) операциями Идеальной математики, задающей чёткий и абсолютный ритм всему: «…левой! …левой! …». Кто там шагает «правой»?

Литература

1. Клюйков С.Ф. Числа и познание мира.- Мариуполь: Полиграфический центр газеты «ИнформМеню». 1997.- 112с.

2. Клюйков С.Ф. Основи математики системою аксіом, що розширюється // Матеріали IV Міжнародної науково-практичної конференції «Динаміка наукових досліджень '2005». 20-30 червня 2005. Том 26 Математика. – Дніпропетровськ: Наука і освіта. 2005.- С.25-36.

3. Клюйков Р.С., Клюйков С.Ф. Языки программирования и Идеальная математика // Materialy V Miedzynarodowej naukowi-praktycznej konferencji “Naukowa przestzen Europy - 2009”. Volume 17 Matemamyka. Nowoczesne informacyjne technologie.- Przemysl: Nauka i studia. 2009. – 96 str, С 3-16.