МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ИНФОРМАЦИИ
1. Количество информации, и ее мера
На вход системы передачи информации (СПИ) от источника информации подается совокупность сообщений, выбранных из ансамбля сообщений (рис. 1).
Помехи
  x1
y1 x1
y1
x2
y2
……
xn
yn
Рис. 1. Система передачи информации
Ансамбль сообщений
– множество возможных сообщений с их вероятностными характеристиками – {Х, р(х)}
. При этом: Х={х1
, х2
,…, хm
}
– множество возможных сообщений источника; i = 1, 2,…, m
, где m
– объем алфавита; p(xi
)
– вероятности появления сообщений, причем p(xi
)
³
0
и поскольку вероятности сообщений представляют собой полную группу событий, то их суммарная вероятность равна единице
 . .
Каждое сообщение несет в себе определенное количество информации. Определим количество информации, содержащееся в сообщении xi
, выбранном из ансамбля сообщений источника {Х, р(х)}.
Одним из параметров, характеризующих данное сообщение, является вероятность его появления – p(xi
)
, поэтому естественно предположить, что количество информации I(xi
)
в сообщении xi
является функцией p(xi
).
Вероятность появления двух независимых сообщений x1
и x2
равна произведению вероятностей p(x1
,x2
) = p(x1
).p(x2
)
, а содержащаяся в них информация должна обладать свойством аддитивности, т.е.:
I(x1
, x2
) = I(x1
)+I(x2
).
(1)
Поэтому для оценки количества информации предложена логарифмическая мера:
 . (2) . (2)
При этом наибольшее количество информации содержат наименее вероятные сообщения, а количество информации в сообщении о достоверном событии равно нулю. Т. к. все логарифмы пропорциональны, то выбор основания определяет единицу информации: loga
x = logb
x/logb
a.
В зависимости от основания логарифма используют следующие единицы информации:
2 – [бит] (bynary digit
– двоичная единица), используется при анализе ин-формационных процессов в ЭВМ и др. устройствах, функционирующих на основе двоичной системы счисления;
e – [нит] (natural digit
– натуральная единица), используется в математических методах теории связи;
10 – [дит] (decimal digit
– десятичная единица), используется при анализе процессов в приборах работающих с десятичной системой счисления.
Битом
(двоичной единицей информации) – называется количество информации, которое снимает неопределенность в отношении наступления одного из двух равновероятных, независимых событий.
Среднее количество информации для всей совокупности сообщений можно получить путем усреднения по всем событиям:
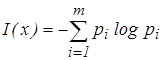 . (3) . (3)
Количество информации, в сообщении, состоящем из n
не равновероятных его элементов равно (эта мера предложена в 1948 г. К. Шенноном):
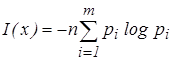 . (4) . (4)
Для случая независимых равновероятных событий количество информации определяется (эта мера предложена в 1928 г. Р. Хартли):
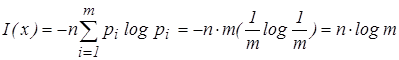 .
(5)
.
(5)
2. Свойства количества информации
1. Количество информации в сообщении обратно – пропорционально вероятности появления данного сообщения.
2. Свойство аддитивности – суммарное количество информации двух источников равно сумме информации источников.
3. Для события с одним исходом количество информации равно нулю.
4. Количество информации в дискретном сообщении растет в зависимости от увеличения объема алфавита – m
.
Пример 1.
Определить количество информации в сообщении из 8 двоичных символов (n
= 8, m
= 2), если вероятности равны: pi0
= pi1
= 1/2.
Количество информации равно:
I = n log m = 8 log2
2 = 8
бит
.
Пример 2.
Определить количество информации в сообщении из 8 двоичных символов (n
= 8, m
= 2), если вероятности равны:
pi0
=
3/4; pi1
= 1/4.
Количество информации равно:
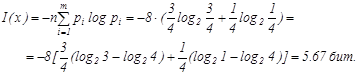
3. Энтропия информации
Энтропия
– содержательность, мера неопределенности информации.
Энтропия
– математическое ожидание H(x)
случайной величины I(x)
определенной на ансамбле {Х, р(х)}
, т.е. она характеризует среднее значение количества информации, приходящееся на один символ.
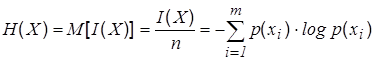 . (6) . (6)
Определим максимальное значение энтропии Hmax
(x)
.Воспользуемся методом неопределенного множителя Лагранжа -l для отыскания условного экстремума функции [6]. Находим вспомогательную функцию:
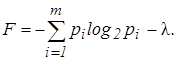 (7)
(7)
Представим вспомогательную функцию F
в виде:
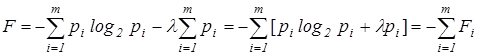 . (8) . (8)
Найдем максимум этой функции
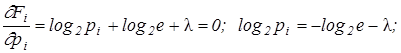 т. к. т. к.
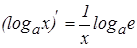 . .
Как видно из выражения, величина вероятности pi
не зависит от i
, а это может быть в случае, если все pi
равны, т.е. p1
=p2
=…=pm
=1/m
.
При этом выражение для энтропии равновероятных, независимых элементов равно:
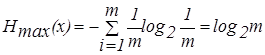 . (9) . (9)
Найдем энтропию системы двух альтернативных событий с вероятностями p1
и p2
. Энтропия равна
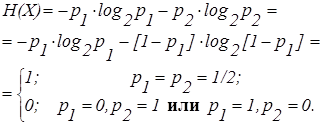
4. Свойства энтропии сообщений
1. Энтропия есть величина вещественная, ограниченная, не отрицательная, непрерывная на интервале 0
£
p
£
1
.
2. Энтропия максимальна для равновероятных событий.
3. Энтропия для детерминированных событий равна нулю.
4. Энтропия системы двух альтернативных событий изменяется от 0 до 1.
Энтропия численно совпадает со средним количеством информации но принципиально различны, так как:
H(x)
– выражает среднюю неопределенность состояния источника и является его объективной характеристикой, она может быть вычислена априорно, т.е. до получения сообщения при наличии статистики сообщений.
I(x)
– определяется апостериорно, т.е. после получения сообщения. С получением информации о состоянии системы энтропия снижается.
5. Избыточность сообщений
Одной из информационных характеристик источника дискретных сообщений является избыточность, которая определяет, какая доля максимально-возможной энтропии не используется источником
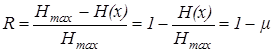 , (10) , (10)
где ?
– коэффициент сжатия.
Избыточность приводит к увеличению времени передачи сообщений, уменьшению скорости передачи информации, излишней загрузки канала, вместе с тем, избыточность необходима для обеспечения достоверности передаваемых данных, т.е. надежности СПД, повышения помехоустойчивости. При этом, применяя специальные коды, использующие избыточность в передаваемых сообщениях, можно обнаружить и исправить ошибки.
Пример 1.
Вычислить энтропию источника, выдающего два символа 0 и 1 с вероятностями p(0) = p(1) = 1/m
и определить его избыточность.
Решение:
Энтропия для случая независимых, равновероятных элементов равна: H(x) = log2
m = log2
2 = 1 [дв. ед/симв.]
При этом H(x) = Hmax
(x)
и избыточность равна R = 0
.
Пример 2.
Вычислить энтропию источника независимых сообщений, выдающего два символа 0 и 1 с вероятностями p(0) = 3/4, p(1) = 1/4
.
Решение:
Энтропия для случая независимых, не равновероятных элементов равна:
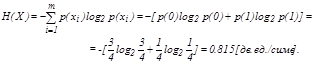
При этом избыточность равна R = 1–0,815=0,18
Пример 3.
Определить количество информации и энтропию сообщения из пяти букв, если число букв в алфавите равно 32 и все сообщения равновероятные.
Решение:
Общее число пятибуквенных сообщений равно: N = mn
= 32
Энтропия для равновероятных сообщений равна:
H
=
I
= –
log
2
1/
N
=
log
2
325
= 5
log
2
32 = 25 бит./симв.
Литература
1 Гринченко А.Г. Теория информации и кодирование: Учебн. пособие. – Харьков: ХПУ, 2000.
2 Цымбал В.П. Теория информации и кодирование. – М.: Высш. шк., 1986.
3 Кловский Д.Д. Теория передачи сигналов. – М.: Связь, 1984.
4 Кудряшов Б.Д. Теория информации. Учебник для вузов Изд-во ПИТЕР, 2008. – 320 с.
5 Цымбал В.П. Теория информации и кодирование. – М.: Высш. шк., 1986.
6 Асанов М.О., Баранский В.А., Расин В.В. Дискретная математика: графы матроиды, алгоритмы. – Ижевск: НИЦ «РХД», 2001, 288 стр.
|