КУРСОВОЙ ПРОЕКТ
по предмету «Моделирование производственных и экономических процессов»
студента группы 1ПМ-03
Литюка Александра Сергеевича
код 2372
2006
Министерство образования и науки Украины
Восточноукраинский национальный университет
имени Владимира Даля
Колледж
Специальность : «Прикладная математика»
ПРОЕКТИРОВАНИЕ МОДЕЛИ ДЛЯ ОПРЕДЕЛЕНТЯ ВРЕМЕНИ ПРОСТОЯ СТАНКОВ НА МАШИНОСТРОИТЕЛЬНОМ ПРЕДПРИЯТИИ
Пояснительная записка
КП.5.080202.МП.15.02.ПЗ
Руководитель
____________ Латкова А.А.
15.12.06.
Выполнил студент
группы 1ПМ-03
____________ Литюк А.С.
11.12.06.
2006
15.02 Министерство обраования и науки Украины
Восточноукраинский науциональный университет
имени Владимира Даля
Колледж
ЗАДАНИЕ
Для курсового проекта
по предмету “Моделирование производственных и экономических процессов”
Студента специальности 5.080202
группы 1ПМ-03___________________
Литюку Александру Сергеевичу__________________________________
Тема задания: «Проектирование модели для определения времени простоя станков на машиностроительном предприятии»_______________________
__________________________________________________________________________________________________________________
Литература
1.Ляшенко И.Н.Линейное и нелинейное программирование.– Киев: Вища школа ,1975.-370с _________________________________________________
2.Дегтярев Ю.И. Исследование операций –Москва: Вища школа ,1986_________
3.Балашевич В.А._____________________________________________
_________________________________________________________
Курсовой проект на указанную тему выполняется в следующем обьеме _________________________________________________________
1 Пояснительная записка
Введение
1 Постановка задачи о переналадке станков как задачи динамического программирования.
2 Методы решения задачи. Метод ветвей и границ.
3 Алгоритм метода ветвей и границ. Схема алгоритма
4 Решение поставленной задачи
4.1 Условие задачи
4.2 Решение задачи вручную
5 Выводы
Литература
Приложения (текст программы, схема программы, расшифровка переменных, описание программы, инструкция пользователю, входная и выходная информация)
2 Расчетная часть
Задача
Определить оптимальную последовательность запуска деталей в производство, если задана матрица затрат на переналадку оборудования:
| № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
∞ |
21 |
11 |
18 |
8 |
15 |
9 |
| 2 |
19 |
∞ |
8 |
3 |
7 |
15 |
25 |
| 3 |
13 |
18 |
∞ |
16 |
1 |
13 |
20 |
| 4 |
16 |
5 |
14 |
∞ |
26 |
14 |
17 |
| 5 |
17 |
9 |
5 |
6 |
∞ |
12 |
19 |
| 6 |
19 |
7 |
21 |
13 |
24 |
∞ |
21 |
| 7 |
10 |
29 |
25 |
11 |
14 |
17 |
∞ |
Сделать анализ решенной задачи.
3 Графическая часть
Лист1 Схема алгоритма метода ветвей и границ_____________________
_________________________________________________________
Лист2 Схема программы_______________________________________
Дата выдачи «_1_»_____09______2006г.
Срок окончания «15»______11____2006г.
Зав. отделением ______________
Руководитель проекта ______________
УТВЕРЖДАЮ
Зав. отделением
……………………………….
«__»_________200_г.
График
работы над курсовым проектом
студента группы 1ПМ-03 Литюка А.С.
№№
п-п
|
Разделы, графы проекта |
Характер работы |
Объём работы |
Срок выполения |
Отметка руководителя о выполнении |
| 1 |
Введение |
Опис. часть |
5 |
1.09-5.09 |
| 2 |
Постановка задачи |
Опис. часть |
5 |
6.09-17.09 |
| 3 |
Методы решения задачи |
Опис. часть |
9 |
18.09-20.09 |
| 4 |
Алгоритм метода ветвей и границ |
Опис. часть |
9 |
21.09-22.09 |
| 5 |
Схема алгоритма |
Граф. часть |
4 |
23.09-24.09 |
| 6 |
Решение поставленной задачи |
Расчет. часть |
13 |
25.09-30.09 |
| 7 |
Составление программы |
Расч. на ЭВМ |
20 |
1.10-15.10 |
| 8 |
Отладка программы |
Расч. на ЭВМ |
17 |
16.10-19.10 |
| 9 |
Инструкция пользователю |
Опис. часть |
2 |
20.10-24.10 |
| 10 |
Граф-кая часть А1 |
Граф. часть |
5 |
25.10-26.10 |
| 11 |
Оформл. Тит.л. и л. содержания |
Графич. часть |
4 |
27.10-1.11 |
| 12 |
Выводы |
Опис. часть |
2 |
2.11-6.11 |
| 13 |
Оформление курсового проекта |
5 |
7.11-8.11 |
Срок сдачи проекта на проверку __9.11-15.11________
День защиты проекта_____16.11-24.11_____________
Руководитель______________________________
Содержание
Введение
1 Постановка задачи о переналадке станков как задачи линейного программирования
2 Методы решения задачи. Метод ветвей и границ
3 Алгоритм метода ветвей и границ. Схема алгоритма
4 Решение поставленной задачи
4.1 Условие задачи
4.2 Решение задачи вручную
5 Выводы
Литература
Приложение А Текст программы
Схема алгоритма
Описание программы
Инструкция пользоватедлю
Приложение Б Входная информация
Выходная информация
Приложение В Графическая часть (1А1)
ВВЕДЕНИЕ
Наиболее распространенная форма организации основного процесса производства-переменно-поточное производство, отличительная особенность которого заключается в периодической перенастройке (переналадке) всего процесса в связи с переходом на другой вид изделий.
Переход с изготовления изделий одного вида на другой (с одной серии на другую) сопровождается потерями и дополнительными издержками производства, к числу которых относятся потери от простоев оборудования, потери от брака в начальный период перехода, расходы по управлению производством.
По существу на любом предприятии каждая из поточных линий время от времени вынуждена перестраиваться с выработки изделий одного вида на другой. Каждый переход, независимо от того, после какой по размеру серии он происходит, вызывает потери времени и дополнительные расходы. Причем суммарные потери, связанные с заданной серией переходов, зависят от последовательности переходов. Если бы этой зависимости не было, то суммарные потери равнялись бы во всех последовательностях одному и тому же числу, и не возникло бы проблемы установления оптимальной последовательности запуска деталей.
1 ПОСТАНОВКА ЗАДАЧИ О ПЕРЕНАЛАДКЕ СТАНКОВ КАК ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Наибольшее распространение в решении задачи календарного планирования обработки т деталей на п станках имеют приближенные методы, основанные главным образом на использовании различных правил предпочтения. Лишь в последнее время стали появляться методы, гарантирующие сходимость к точному решению за конечное число шагов. Рассмотрим один из таких методов, базирующийся на идеях метода ветвей и границ.
Пусть на участке с последовательным движением производства обрабатываются детали с одинаковыми технологическими маршрутами. Передача деталей со станка на станок осуществляется транспортными партиями, совпадающими с партиями обработки. Задана матрица  , где , где 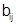 —продолжительность обработки партии деталей i-го наименования на j-м станке. В один и тот же момент на станке обрабатывается только одна деталь. Требуется найти календарное расписание работы участка в виде матриц —продолжительность обработки партии деталей i-го наименования на j-м станке. В один и тот же момент на станке обрабатывается только одна деталь. Требуется найти календарное расписание работы участка в виде матриц 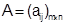 и и 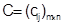 , элементы которых показывают соответственно время начала и окончания обработки каждой детали на каждом станке. Из всех допустимых расписаний необходимо выбрать обеспечивающее наименьшую совокупную длительность производственного цикла обработки всех деталей. , элементы которых показывают соответственно время начала и окончания обработки каждой детали на каждом станке. Из всех допустимых расписаний необходимо выбрать обеспечивающее наименьшую совокупную длительность производственного цикла обработки всех деталей.
При описании алгоритма решения будет использовано понятие «конфликтующие детали». Его сущность можно пояснить на примере. Пусть для матрицы продолжительностей обработки
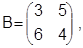
составлено расписание окончания обработки

Из анализа матрицы С видно, что для каждой отдельной детали расписание се обработки является наилучшим, так как обработка планируется таким образом, чтобы детали не пролеживали. В то же время это расписание недопустимо, так как имеются отрезки времени, когда на одном станке должны обрабатываться обе детали одновременно — детали «конфликтуют». Действительно, на первом станке предусмотрена обработка одной детали в интервале (0—3), а другой — в интервале (0—6), на втором станке первая деталь обрабатывается в интервале (3—8). а вторая — в интервале (С—10).
Следовательно, возникает конфликт, который можно ликвидировать, сделав расписание допустимым за счет предпочтения какой-либо детали. Если отдать предпочтение первой детали, расписание примет вид
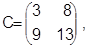
а если второй, то время окончания операций будет
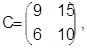
В первом случае совокупная длительность никла 13 часов. во втором— 15. Следовательно, главный вопрос при разрешении конфликта состоит в выборе детали, которой следует отдать предпочтение для обработки на данном станке. В общем случае любая деталь на некотором станке может конфликтовать с несколькими другими. Ниже на числовом примере рассматривается процесс последовательного устранения конфликтов, приводящий в соответствии со схемой метода ветвей и границ к допустимому оптимальному расписанию работы оборудования.
Пусть дана матрица продолжительностей обработки четырех партий деталей на трех станках
 , ,
Требуется определить порядок обработки партий деталей на каждом станке, обеспечивающий наименьшую длительность совокупного цикла.
Первый шаг. Составляем для каждой отдельно взятой детали наилучшее расписание времени окончания ее обработки на каждом из станков в виде матрицы С, элементы которой
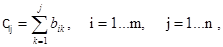
определяются исходя из возможности обработки каждой детали без пролеживания.
Получаем матрицу
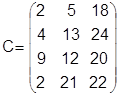 . .
Второй шаг. Проверяем наличие конфликта на первом станке. Поскольку каждая деталь рассматривалась независимо от остальных, то их обработка на первом станке начинается одновременно и протекает в промежутки времени (0—2). (0—4), (0—9). (0—2). Следовательно, все детали конфликтуют друг с другом.
Третий шаг. Разрешая поочередно конфликт в пользу каждой из деталей, находим ту деталь, которую целесообразно на первом станке обрабатывать первой. Для этого выполняем т раз следующие два действия.
1. Строим календарное расписание 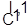 окончания обработки деталей на каждой операции при условии, что на первом станке деталь l запускается первой. окончания обработки деталей на каждой операции при условии, что на первом станке деталь l запускается первой.
Элементы этой матрицы определяются из соотношения
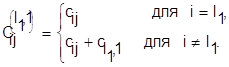
Предположим, что деталь 1 запускается на первом станке первой. Тогда
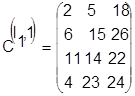 . .
В результате деталь 1 не конфликтует ни с какими другими деталями на нервом станке.
2. Каждому календарному расписанию 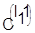 приписываем его оценку приписываем его оценку 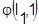 в виде минимально возможного времени окончания Обработки деталей на последнем станке n в предположении, что на первых п — 1 станках конфликты отсутствуют. в виде минимально возможного времени окончания Обработки деталей на последнем станке n в предположении, что на первых п — 1 станках конфликты отсутствуют.
Из матрицы 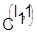 известно возможное время начала обработки любой детали i на последнем станке. Оно совпадает с временем известно возможное время начала обработки любой детали i на последнем станке. Оно совпадает с временем 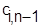 окончания ее обработки на предпоследнем станке. окончания ее обработки на предпоследнем станке.
Чтобы не увеличивать длительность обработки деталей, целесообразно на последнем станке обрабатывать детали в очередности их поступления на этот станок
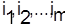 , ,
где

Оценка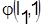 определяется следующим образом. определяется следующим образом.
Первоначально сравниваем 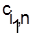 с с  . .
Если  , то время завершения обработки двух деталей i1
и , то время завершения обработки двух деталей i1
и 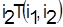 на последней операции будет равно времени окончания обработки детали i2
, т. е. на последней операции будет равно времени окончания обработки детали i2
, т. е.
 . .
Если 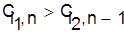 , то , то  . .
Далее сравниваем время завершения обработки на последнем станке двух первых деталей i1
и i2
с временам завершения обработки на предпоследнем стачке детали i3
.Здесь возможны два случая:
1) если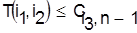 ., то ., то  ; ;
2) если  , то , то 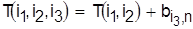 , и т.д. , и т.д.
В результате такого цепного расчета получим минимально возможное время обработки всех деталей 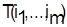 для варианта расписания для варианта расписания 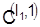 предположении, что все конфликты в нем на первых п — 1 станках устранены. Эту величину и принимаем за нижнюю границу времени окончания обработки деталей по расписанию предположении, что все конфликты в нем на первых п — 1 станках устранены. Эту величину и принимаем за нижнюю границу времени окончания обработки деталей по расписанию 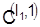
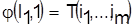 . .
Как видно из матрицы 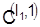 , моменты завершения обработки деталей на предпоследнем, втором станке упорядочены следующим образом: , моменты завершения обработки деталей на предпоследнем, втором станке упорядочены следующим образом:
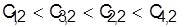 , ,
т. е. детали на последний станок поступают в очередности 1, 3, 2, 4. Выбираем первые две детали 1 и 3 и определяем момент завершения их обработки на последнем станке.
Так как 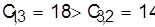 , то , то 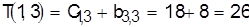 . .
Включаем в рассмотрение третью по порядку деталь 2. Поскольку, 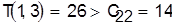 то минимально возможное время обработки первых трех деталей (1, 3, 2) будет то минимально возможное время обработки первых трех деталей (1, 3, 2) будет
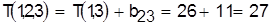 . .
Рассматривая последнюю деталь, видим, что 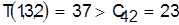 . .
Следовательно,  . .
Отсюда получаем
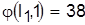 . .
Повторим действия I и 2 для остальных вариантов, когда первой на первом станке обрабатывается деталь 2, 3 или 4.
Разрешая конфликт в пользу детали 2, получаем
 , , 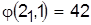 . .
Отдавая предпочтение па первом станке детали 3, получаем расписание и его опенку в виде
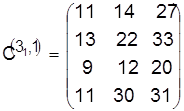 , , 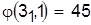 . .
Разрешаем конфликт в пользу детали 4:
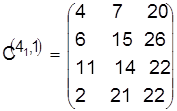 , , 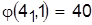 . .
3. Сопоставляем расписания 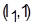 , , 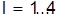 и их оценки и их оценки 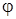 с вершинами дерева, изображающего процесс ветвления всего множества вариантов расписания на подмножества (рисунок 1). с вершинами дерева, изображающего процесс ветвления всего множества вариантов расписания на подмножества (рисунок 1).
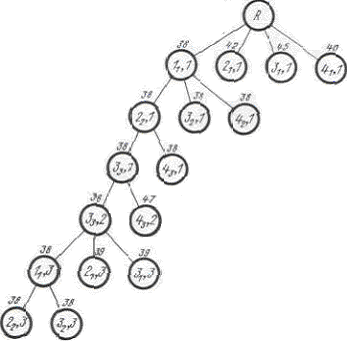
Рисунок 1
Из всех рассмотренных календарных расписаний 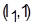 выбираем такое выбираем такое 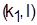 , для которого , для которого
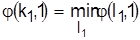 . .
Поскольку наименьшей оценкой является 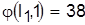 , предпочтение к запуску на первом станке отдается детали l=1. Остальные m-1=3 детали продолжают конфликтовать па первом станке. , предпочтение к запуску на первом станке отдается детали l=1. Остальные m-1=3 детали продолжают конфликтовать па первом станке.
Четвертый шаг. В качестве исходного календарного расписания для дальнейших расчетов берем матрицу 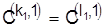 , на основе которой будем определять деталь, подлежащую запуску на нервом станке второй. Для этого построим календарные расписания в виде матриц , на основе которой будем определять деталь, подлежащую запуску на нервом станке второй. Для этого построим календарные расписания в виде матриц 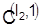 , элементы которых находятся по правилу , элементы которых находятся по правилу

Разрешая конфликты для каждой из т—1 оставшейся детали на первом станке, получим нижнюю границу для каждого расписания 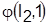 и выберем из всех расписаний то, для которого и выберем из всех расписаний то, для которого
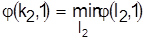 . .
Детальk2
планируется к обработке второй. Выполним эти расчеты для нашего примера.
Разрешая конфликт для детали 2, построим для нее календарное расписание с учетом того, что деталь 1 уже назначена к обработке первой, и найдем его нижнюю границу. Получим
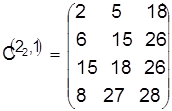 , , 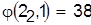 . .
Разрешаем конфликт в пользу детали 3:
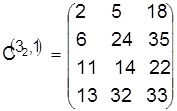 , , 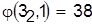 . .
Разрешаем конфликт в пользу детали 4:
 , , 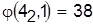 . .
Сопоставим полученные расписания и их оценки с вершинами дерева, разливаемыми из вершины 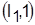 (рисунок 1). (рисунок 1).
Так как оценки для всех вариантов одинаковы, безразлично, какой из деталей отдать предпочтение. Пусть деталь 2 планируется к запуску на первом станке второй.
Пятый шаг.
Аналогичным образом определим деталь, запускаемую на первом станке третьей.
Разрешаем конфликт относительно детали 3:
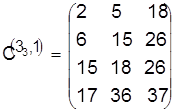 , ,  . .
Разрешаем конфликт относительно детали 4:
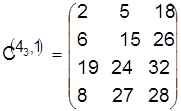 , , 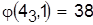 . .
Сопоставляем полученные расписания и их оценки с вершинами дерева, развиваемыми из вершины 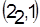 (рисунок 1). Так как оценки, связанные с запуском на первом станке трех первых детален в очередности 1, 2, 3 или 1, 2, 4, одинаковы, безразлично, какой из них отдать предпочтение. Пусть выбрана первая из них, k3
=3, тогда последовательность обработки деталей на первом станке будет 1, 2, 3, 4, с нижней границей, равной 38. (рисунок 1). Так как оценки, связанные с запуском на первом станке трех первых детален в очередности 1, 2, 3 или 1, 2, 4, одинаковы, безразлично, какой из них отдать предпочтение. Пусть выбрана первая из них, k3
=3, тогда последовательность обработки деталей на первом станке будет 1, 2, 3, 4, с нижней границей, равной 38.
Шестой шаг. В результате предыдущих шагов получено календарное расписание 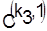 и последовательность запуска партий деталей на первом станке и последовательность запуска партий деталей на первом станке 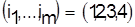 . .
Далее провернем и последовательно разрешаем конфликты на втором станке.
Детали 1, 2, 3, 4 планируются к обработке в интервалах времени соответственно (2—5), (6—15), (15—18),(17—36).
Следовательно, на втором станке деталь 2 запускается после детали I, а детали 3 и 4 конфликтуют.
Разрешим конфликт относительно детали 3.
Для этого на базе 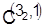 составим расписание, в котором элементы составим расписание, в котором элементы 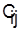 для данной детали и деталей, не участвующих в конфликте, остаются без изменения, а элементы для данной детали и деталей, не участвующих в конфликте, остаются без изменения, а элементы 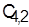 и и  возрастают на величину задержки в поступлении детали 4 на второй станок, которая равна в данном случае разности возрастают на величину задержки в поступлении детали 4 на второй станок, которая равна в данном случае разности 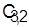 — —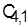 == 1. Получим расписание и оценку нижней границы: == 1. Получим расписание и оценку нижней границы:
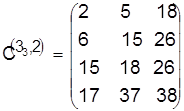 , , 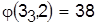 . .
Разрешая конфликт в пользу детали 4, задерживаем подачу детали 3 ко второму станку на 36—15=21, в результате чего расписание и его оценка принимают вид
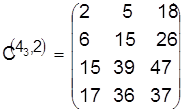 , , 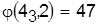 . .
Сопоставляя эти расписания и оценки с вершинами графа, развиваемыми из вершины 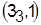 , выбираем расписание , выбираем расписание  , предусматривающее обработку на втором станке третьей по порядку детали 3. , предусматривающее обработку на втором станке третьей по порядку детали 3.
Таким образом, на этом шаге упорядочена очередность запусков партий на втором станке в виде последовательности деталей 1. 2, 3, 4 с оценкой времени совокупного цикла 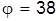 . .
Седьмой шаг. Отправляясь от расписания  , проверяем наличие конфликтующих детален на третьем станке. , проверяем наличие конфликтующих детален на третьем станке.
Детали 1, 2, 3, 4 планируются к обработке в интервалах времени соответственно (5—18), (15—26), (18—26),(37—38).
Конфликтуют три первые детали. Разрешаем конфликт в пользу детали 1:
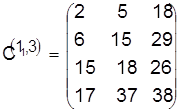 , , 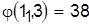 . .
Разрешаем конфликт в пользу детали 2:
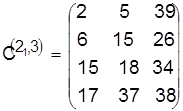 , , 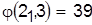 . .
Разрешаем конфликт в пользу детали 3:
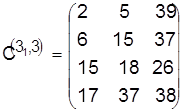 , , 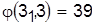 . .
Разветвляем вершину  дерева решений (рисунок 1) в соответствии с полученными оценками. Для определения детали, запускаемой па третьем станке второй, выбираем расписание дерева решений (рисунок 1) в соответствии с полученными оценками. Для определения детали, запускаемой па третьем станке второй, выбираем расписание 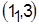 , имеющее меньшую нижнюю границу. , имеющее меньшую нижнюю границу.
Рассматривая его, видим, что на третьем станке конфликтуют детали 2 и 3, обрабатываемые в интервалы времени соответственно (15—29) и (18—26).
Разрешим конфликт, отдавая предпочтение детали 2.
Получим расписание и его оценку:
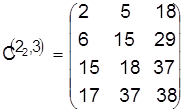 , , 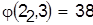 . .
Разрешим конфликт в пользу детали 3:
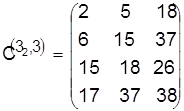 , , 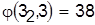 . .
Таким образом, безразлично, какой детали отдать предпочтение. Пусть второй обрабатывается деталь 2. Проверяя расписание 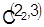 , устанавливаем отсутствие конфликтов па третьем станке. , устанавливаем отсутствие конфликтов па третьем станке.
Мы нашли один из вариантов календарного расписания. Чтобы убедиться в его оптимальности, рассмотрим дерево ветвлений и проанализируем значения нижних границ для всех его оборванных ветвей. Поскольку все нижние оценки не меньше полученной, считаем расписание 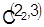 оптимальным. Начало времени обработки партий деталей оптимальным. Начало времени обработки партий деталей
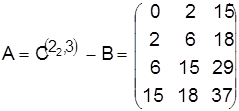 . .
Календарный график работы оборудования, соответствующий расписаниям 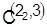 и А.. и А..
Цифры над прямоугольниками — номера деталей, внутри прямоугольника — время начала и окончания обработки партии деталей.
2 МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ. МЕТОД ВЕТВЕЙ И ГРАНИЦ
Комбинаторика
– раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного множества в соответствии с заданными правилами.
Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией
. Поэтому можно сказать, что целью комбинаторного анализа является изучение комбинаторных конфигураций. Это изучение включает в себя вопросы существования комбинаторных конфигураций, алгоритмы их построения, оптимизацию таких алгоритмов, а также решение задач перечисления, в частности определение числа конфигураций данного класса. Простейшим примером комбинаторных конфигураций являются перестановки, сочетания и размещения.
Большой вклад в систематическое развитие комбинаторных методов был сделан Г. Лейбницем (диссертация “Комбинаторное искусство”), Я. Бернулли (работа “Искусство предположений”), Л. Эйлером. Можно считать, что с появлением работ Я. Бернулли и Г. Лейб-ница комбинаторные методы выделились в самостоятельную часть математики. В работах Л.Эйлера по разбиениям и композициям натуральных чисел на слагаемые было положено начало одному из основных методов перечисления комбинаторных конфигураций – методу производящих функций.
Возвращение интереса к комбинаторному анализу относится к 50-м годам ХХ в. в связи с бурным развитием кибернетики и дискретной математики и широким использованием электронно-вычислительной техники. В этот период активизировался интерес к классическим комбинаторным задачам.
Классические
комбинаторные
задачи
– это задачи выбора и расположения элементов конечного множества, имеющие в качестве исходной некоторую формулировку развлекательного содержания типа головоломок.
В 1859 г. У. Гамильтон придумал игру “Кругосветное путешествие”, состоящую в отыскании такого пути, проходящего через все вершины (города, пункты назначения) графа, изображенного на рис. 1, чтобы посетить каждую вершину однократно и возвратиться в исходную. Пути, обладающие таким свойством, называются гамильтоновыми циклами
.
Задача о гамильтоновых циклах в графе получила различные обобщения. Одно из этих обобщений – задача коммивояжера
, имеющая ряд применений в исследовании операций, в частности при решении некоторых транспортных проблем.
Задача коммивояжера (в дальнейшем сокращённо - ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё, как об Великую теорему Ферма обламывали зубы лучшие математики. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы.
Постановка задачи следующая.
Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,1,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?
Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jÎТ=(1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t=(j1
,j2
,..,jn
,j1
), причём все j1
..jn
– разные номера; повторяющийся в начале и в конце j1
,показывает, что перестановка зациклена. Расстояния между парами вершин Сij
образуют матрицу С. Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать функционал
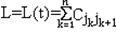
Относительно математизированной формулировки ЗК уместно сделать два замечания.
Во-первых, в постановке Сij
означали расстояния, поэтому они должны быть неотрицательными, т.е. для всех jÎТ:
(последнее равенство означает запрет на петли в туре), симметричными, т.е. для всех i,j:
и удовлетворять неравенству треугольника, т.е. для всех:
В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных задач, которые описываются основной моделью, но всем условиям (2)-(4) не удовлетворяют. Особенно часто нарушается условие (3) (например, если Сij
– не расстояние, а плата за проезд: часто туда билет стоит одну цену, а обратно – другую). Поэтому мы будем различать два варианта ЗК: симметричную задачу, когда условие (3) выполнено, и несимметричную - в противном случае. Условия (2)-(4) по умолчанию мы будем считать выполненными.
Второе замечание касается числа всех возможных туров. В несимметричной ЗК все туры t=(j1
,j2
,..,jn
,j1
) и t’=(j1
,jn
,..,j2
,j1
) имеют разную длину и должны учитываться оба. Разных туров очевидно (n-1)!.
Зафиксируем на первом и последнем месте в циклической перестановке номер j1
, а оставшиеся n-1 номеров переставим всеми (n-1)! возможными способами. В результате получим все несимметричные туры. Симметричных туров имеется в два раз меньше, т.к. каждый засчитан два раза: как t и как t’.
Можно представить, что С состоит только из единиц и нулей. Тогда С можно интерпретировать, как граф, где ребро (i,j) проведено, если Сij
=0 и не проведено, если Сij
=1. Тогда, если существует тур длины 0, то он пройдёт по циклу, который включает все вершины по одному разу. Такой цикл называется гамильтоновым циклом. Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём).
В терминах теории графов симметричную ЗК можно сформулировать так:
Дана полная сеть с nвершинами, длина ребра (i,j)=Сij
. Найти гамильтонов цикл минимальной длины.
В несимметричной ЗК вместо “цикл” надо говорить “контур”, а вместо “ребра” - “дуги” или “стрелки”.
Некоторые прикладные задачи формулируются как ЗК, но в них нужно минимизировать длину не гамильтонова цикла, а гамильтоновой цепи. Такие задачи называются незамкнутыми. Некоторые модели сводятся к задаче о нескольких коммивояжерах, но мы здесь их рассматривать не будем.
Жадный алгоритм
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. “Жадным” этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.
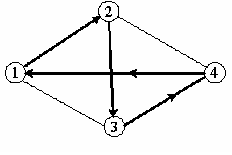
Рисунок 3
Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию “иди в ближайший (в который еще не входил) город”. Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рисунке 3, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм “иди вы ближайший город” выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
В пользу процедуры “иди в ближайший” можно сказать лишь то, что при старте из одного города она не уступит стратегии “иди в дальнейший”.
Как видим, жадный алгоритм ошибается. Можно ли доказать, что он ошибается умеренно, что полученный им тур хуже минимального, положим, в 1000 раз? Мы докажем, что этого доказать нельзя, причем не только для жадного алгоритма, а для алгоритмов гораздо более мощных. Но сначала нужно договориться, как оценивать погрешность неточных алгоритмов, для определенности, в задаче минимизации. Пусть fB
- настоящий минимум, а fA
- тот квазиминимум, который получен по алгоритму. Ясно, что fA
/fB
≥1, но это – тривиальное утверждение, что может быть погрешность. Чтобы оценить её, нужно зажать отношение оценкой сверху:
где, как обычно в высшей математике, ε≥0, но, против обычая, может быть очень большим. Величина ε и будет служить мерой погрешности. Если алгоритм минимизации будет удовлетворять неравенству (5), мы будем говорить, что он имеет погрешность ε.
Предположим теперь, что имеется алгоритм А решения ЗК, погрешность которого нужно оценить. Возьмем произвольный граф G (V,E) и по нему составим входную матрицу ЗК:
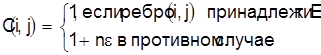
Если в графе G есть гамильтонов цикл, то минимальный тур проходит по этому циклу и fB
= n. Если алгоритм А тоже всегда будет находить этот путь, то по результатам алгоритма можно судить, есть ли гамильтонов цикл в произвольном графе. Однако, непереборного алгоритма, который мог бы ответить, есть ли гамильтонов цикл в произвольном графе, до сих пор никому не известно. Таким образом, наш алгоритм А должен иногда ошибаться и включать в тур хотя бы одно ребро длины 1+nε. Но тогда fA
³(n-1)+(1+nε) так что fA
/fB
=1+nε т.е. превосходит погрешность ε на заданную неравенством (5). О величине ε в нашем рассуждении мы не договаривались, так что ε может быть произвольно велик.
Таким образом доказана следующая теорема.
Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.
Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (4).
Если оно соблюдается, можно предложить несколько алгоритмов с погрешностью 12. Прежде, чем описать такой алгоритм, следует вспомнить старинную головоломку. Можно ли начертить одной линией открытый конверт? На рисунке 4 видно, что можно (цифры на отрезках показывают порядок их проведения). Закрытый конверт одной линией нарисовать нельзя и вот почему. Будем называть линии ребрами, а их перекрестья – вершинами. 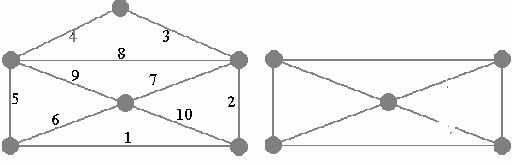
Рисунок 4
Когда через точку проводится линия, то используется два ребра – одно для входа в вершину, одно – для выхода. Если степень вершины нечетна – то в ней линия должна начаться или кончиться. На рис. 3 вершин нечетной степени две: в одной линия начинается, в другой – кончается. Однако на рисунке 4 имеется четыре вершины степени три, но у одной линии не может быть четыре конца. Если же нужно прочертить фигуру одной замкнутой линией, то все ее вершины должны иметь четную степень.
Верно и обратное утверждение: если все вершины имеют четную степень, то фигуру можно нарисовать одной незамкнутой линией. Действительно, процесс проведения линии может кончиться, только если линия придет в вершину, откуда уже выхода нет: все ребра, присоединенные к этой вершине (обычно говорят: инцидентные этой вершине), уже прочерчены. Если при этом нарисована вся фигура, то нужное утверждение доказано; если нет, удалим уже нарисованную часть G’. После этого от графа останется одна или несколько связных компонент; пусть G’ – одна из таких компонент. В силу связности исходного графа G, G’ и G’’ имеют хоть одну общую вершину, скажем, v. Если в G’’ удалены какие-то ребра, то по четному числу от каждой вершины. Поэтому G’’ – связный и все его вершины имеют четную степень. Построим цикл в G’’ (может быть, не нарисовав всего G’’) и через v добавим прорисованную часть G’’ к G’. Увеличивая таким образом прорисованную часть G’, мы добьемся того, что G’ охватит весь G.
Эту задачу когда-то решил Эйлер, и замкнутую линию, которая покрывает все ребра графа, теперь называю эйлеровым циклом. По существу была доказана следующая теорема.
Эйлеров цикл в графе существует тогда и только тогда, когда (1) граф связный и (2) все его вершины имеют четные степени.
Деревянный алгоритм
Теперь можно обсудить алгоритм решения ЗК через построение кратчайшего остовного дерева. Для краткости будет называть этот алгоритм деревянным.
Вначале обсудим свойство спрямления. Рассмотрим какую-нибудь цепь, например, на рис.5. Если справедливо неравенство треугольника, то d[1,3]£d[1,2]+d[2,3] и d[3,5]£d[3,4]+d[4,5] Сложив эти два неравенства, получим d[1,3]+d[3,5]£d[1,2]+d[2,3]+d[3,4]+d[4,5]. По неравенству треугольника получим. d[1,5]£d[1,3]+d[3,5]. Окончательно
d[1,5]£d[1,2]+d[2,3]+d[3,4]+d[4,5]
Итак, если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи. Это обобщение расхожего убеждения, что прямая короче кривой.
Вернемся к ЗК и опишем решающий ее деревянный алгоритм.
1. Построим на входной сети ЗК кратчайшее остовное дерево и удвоим все его ребра. Получим граф G – связный и с вершинами, имеющими только четные степени.
2. Построим эйлеров цикл G, начиная с вершины 1, цикл задается перечнем вершин.
3. Просмотрим перечень вершин, начиная с 1, и будем зачеркивать каждую вершину, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.
Теорема. Погрешность деревянного алгоритма равна 1.
Доказательство. Возьмем минимальный тур длины fB
и удалим из него максимальное ребро. Длина получившейся гамильтоновой цепи LHC
меньше fB
. Но эту же цепь можно рассматривать как остовное дерево, т. к. эта цепь достигает все вершины и не имеет циклов. Длина кратчайшего остовного дерева LMT
меньше или равна LHC
. Имеем цепочку неравенств
Но удвоенное дерево – оно же эйлеров граф – мы свели к туру посредством спрямлений, следовательно, длина полученного по алгоритму тура удовлетворяет неравенству
Умножая (6) на два и соединяя с (7), получаем цепочку неравенств
Т.е. 2fB
>fA
, т.е. fA
/fB
>1+e; e=1.
Теорема доказана.
Таким образом, мы доказали, что деревянный алгоритм ошибается менее, чем в два раза. Такие алгоритмы уже называют приблизительными, а не просто эвристическими.
Известно еще несколько простых алгоритмов, гарантирующих в худшем случае e=1. Для того, чтобы найти среди них алгоритм поточнее, зайдем с другого конца и для начала опишем “brute-forceenumeration” - “перебор животной силой”, как его называют в англоязычной литературе. Понятно, что полный перебор практически применим только в задачах малого размера. Напомним, что ЗК с n городами требует при полном переборе рассмотрения (n-1)!/2 туров в симметричной задаче и (n-1)! Туров в несимметричной, а факториал, как показано в следующей таблице, растет удручающе быстро:
| 5! |
10! |
15! |
20! |
25! |
30! |
35! |
40! |
45! |
50! |
| ~102
|
~106
|
~1012
|
~1018
|
~10125
|
~1032
|
~1040
|
~1047
|
~1056
|
~1064
|
Чтобы проводить полный перебор в ЗК, нужно научиться (разумеется, без повторений) генерировать все перестановки заданного числа m элементов. Это можно сделать несколькими способами, но самый распространенный (т.е. приложимый для переборных алгоритмов решения других задач) – это перебор в лексикографическом порядке.
Пусть имеется некоторый алфавит и наборы символов алфавита (букв), называемые словами. Буквы в алфавите упорядочены: например, в русском алфавите порядок букв аµбµя (символ µ читается “предшествует)”. Если задан порядок букв, можно упорядочить и слова. Скажем, дано слово u=(u1
,u2
,..,um
) – состоящее из букв u1
,u2
,..,um
- и слово v =(v1
,v2
,..,vb
). Тогда если u1
µv1,
то и uµv, если же u1
=v1,
то сравнивают вторые буквы и т.д. Этот порядок слов и называется лексикографическим. Поэтому в русских словарях (лексиконах) слово “абажур” стоит раньше слова “абака”. Слово “бур” стоит раньше слова “бура”, потому что пробел считается предшествующим любой букве алфавита.
Рассмотрим, скажем, перестановки из пяти элементов, обозначенных цифрами 1..5. Лексикографически первой перестановкой является 1-2-3-4-5, второй – 1-2-3-5-4, …, последней – 5-4-3-2-1. Нужно осознать общий алгоритм преобразования любой перестановки в непосредственно следующую.
Правило такое: скажем, дана перестановка 1-3-5-4-2. Нужно двигаться по перестановке справа налево, пока впервые не увидим число, меньшее, чем предыдущее (в примере это 3 после 5). Это число, Pi
-1
надо увеличить, поставив вместо него какое-то число из расположенных правее, от Pi
до Pn
. Число большее, чем Pi
-1
, несомненно, найдется, так как Pi
-
1< Pi
. Если есть несколько больших чисел, то, очевидно, надо ставить меньшее из них. Пусть это будет Pj
,j>i-1. Затем число Pi
-
1 и все числа от Pi
до Pn
, не считая Pj
нужно упорядочить по возрастанию. В результате получится непосредственно следующая перестановка, в примере – 1-4-2-3-5. Потом получится 1-4-2-5-3 (тот же алгоритм, но упрощенный случай) и т.д.
Нужно понимать, что в ЗК с n городами не нужны все перестановки из n элементов. Потому что перестановки, скажем, 1-3-5-4-2 и 3-5-4-2-1 (последний элемент соединен с первым) задают один и тот же тур, считанный сперва с города 1, а потом с города 3. Поэтому нужно зафиксировать начальный город 1 и присоединять к нему все перестановки из остальных элементов. Этот перебор даст (n-1)! разных туров, т.е. полный перебор в несимметричной ЗК (мы по-прежнему будем различать туры 1-3-5-4-2 и 1-2-4-5-3).
Данный алгоритм описан на языке Паскаль (см. Приложения).
Пример 2. Решим ЗК, поставленную в Примере 1 лексикографическим перебором. Приведенная выше программа напечатает города, составляющие лучший тур: 1-2-6-5-4-3 и егодлину 36.
Желательно усовершенствовать перебор, применив разум. В следующем пункте описан алгоритм, который реализует простую, но широко применимую и очень полезную идею.
Алгоритм Дейкстры
Одним из вариантов решения ЗК является вариант нахождения кратчайшей цепи, содержащей все города. Затем полученная цепь дополняется начальным городом – получается искомый тур.
Можно предложить много процедур решения этой задачи, например, физическое моделирование. На плоской доске рисуется карта местности, в города, лежащие на развилке дорог, вбиваются гвозди, на каждый гвоздь надевается кольцо, дороги укладываются верёвками, которые привязываются к соответствующим кольцам. Чтобы найти кратчайшее расстояние между i и k, нужно взять I в одну руку и k в другую и растянуть. Те верёвки, которые натянутся и не дадут разводить руки шире и образуют кратчайший путь между i и k. Однако математическая процедура, которая промоделирует эту физическую, выглядит очень сложно. Известны алгоритмы попроще. Один из них – алгоритм Дейкстры, предложенный Дейкстрой ещё в 1959г. Этот алгоритм решает общую задачу:
В ориентированной, неориентированной или смешанной (т. е. такой, где часть дорог имеет одностороннее движение) сети найти кратчайший путь между двумя заданными вершинами.
Алгоритм использует три массива из n (= числу вершин сети) чисел каждый. Первый массив a содержит метки с двумя значениями: 0 (вершина ещё не рассмотрена) и 1 (вершина уже рассмотрена); второй массив b содержит расстояния – текущие кратчайшие расстояния от vi
до соответствующей вершины; третий массив c содержит номера вершин – k-й элемент ck
есть номер предпоследней вершины на текущем кратчайшем пути из vi
в vk
. Матрица расстояний Dik
задаёт длины дуг dik
; если такой дуги нет, то dik
присваивается большое число Б, равное “машинной бесконечности”.
Теперь можно описать:
Алгоритм Дейкстры
1.
Инициализация.
В цикле от одного до n заполнить нулями массив а; заполнить числом i массив с: перенести i-тую строку матрицы D в массив b;
a[i]:=1; c[i]:=0; {i-номер стартовой вершины}
2.
Общий шаг.
Найти минимум среди неотмеченных (т. е. тех k, для которых a[k]=0); пусть минимум достигается на индексе j, т. е. bj
£bk
; a[j]:=1;
если bk
>bj
+djk
то (bk
:=bj
+djk
; ck
:=j) {Условие означает, что путь vi
..vk
длиннее, чем путь vi
..vj
,vk
. Если все a[k] отмечены, то длина пути vi
..vk
равна b[k]. Теперь надо перечислить вершины, входящие в кратчайший путь}
3.
Выдача ответа.
{
Путь vi
..vk
выдаётся в обратном порядке следующей процедурой:}
3.1. z:=c[k];
3.2. Выдать z;
3.3. z:=c[z]; Если z = 0, то конец, иначе перейти к 3.2.
Для выполнения алгоритма нужно nраз просмотреть массив b из n элементов, т. е. алгоритм Дейкстры имеет квадратичную сложность.
Таким образом, для решения ЗК нужно n раз применить алгоритм Дейкстры следующим образом.
Возьмём произвольную пару вершин
j,k. Исключим непосредственное ребро C[j,k]. С помощью алгоритма Дейкстры найдём кратчайшее расстояние между городами j..k. Пусть это расстояние включает некоторый город m. Имеем часть тура j,m,k. Теперь для каждой пары соседних городов (в данном примере – для j,m и m,k) удалим соответственное ребро и найдём кратчайшее расстояние. При этом в кратчайшее расстояние не должен входить уже использованный город.
Далее аналогично находим кратчайшее расстояние между парами вершин алгоритмом Дейкстры, до тех пор, пока все вершины не будут задействованы. Соединим последнюю вершину с первой и получим тур. Чаще всего это последнее ребро оказывается очень большим, и тур получается с погрешностью, однако алгоритм Дейкстры можно отнести к приближённым алгоритмам.
Практическое применение задачи коммивояжера
Кроме очевидного применения ЗК на практике, существует ещё ряд задач, сводимых к решению ЗК.
Задача о производстве красок
.
Имеется производственная линия для производства n красок разного цвета; обозначим эти краски номерами 1,2… n. Всю производственную линию будем считать одним процессором.. Будем считать также, что единовременно процессор производит только одну краску, поэтому краски нужно производить в некотором порядке Поскольку производство циклическое, то краски надо производить в циклическом порядке p=(j1
,j2
,..,jn
,j1
). После окончания производства краски i и перед началом производства краски jнадо отмыть оборудование от краски i. Для этого требуется время C[i,j]. Очевидно, что C[i,j] зависит как от i, так и от j, и что, вообще говоря,C[i,j]≠C[j,i]. При некотором выбранном порядке придется на цикл производства красок потратить время
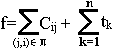
Где tk
- чистое время производства k-ой краски (не считая переналадок). Однако вторая сумма в правой части постоянна, поэтому полное время на цикл производства минимизируется вместе с общим временем на переналадку.
Таким образом, ЗК и задача о минимизации времени переналадки – это просто одна задача, только варианты ее описаны разными словами.
Задача о дыропробивном прессе
. Дыропробивной пресс производит большое число одинаковых панелей – металлических листов, в которых последовательно по одному пробиваются отверстия разной формы и величины. Схематически пресс можно представить в виде стола, двигающегося независимо по координатам x, y, и вращающегося над столом диска, по периметру которого расположены дыропробивные инструменты разной формы и величины. Каждый инструмент присутствует в одном экземпляре. Диск может вращаться одинаково в двух направлениях (координата вращения z). Имеется собственно пресс, который надавливает на подвешенный под него инструмент тогда, когда под инструмент подведена нужная точка листа.
Операция пробивки j-того отверстия характеризуется четверкой чисел (xj
,yj
,zj
,tj
),, где xj
,yj
- координаты нужного положения стола, zj
- координата нужного положения диска и tj
- время пробивки j-того отверстия.
Производство панелей носит циклический характер: в начале и конце обработки каждого листа стол должен находиться в положениях (x0
, y0
) диск в положении z0
причем в этом положении отверстие не пробивается. Это начальное состояние системы можно считать пробивкой фиктивного нулевого отверстия. С параметрами (x0
,y0
,z0
,0).
Чтобы пробить j-тое отверстие непосредственно после i-того необходимо произвести следующие действия:
1. Переместить стол по оси x из положения xi
в положение xj
, затрачивая при этом время t(
x
)
(|xi
-xj
|)=ti
,
j
(
x
)
1. Проделать то же самое по оси y, затратив время ti
,
j
(
y
)
2. Повернуть головку по кратчайшей из двух дуг из положения zi
в положение zj
, затратив время ti
,
j
(
z
)
.
3. Пробить j-тое отверстие, затратив время tj
.
Конкретный вид функций t(
x
)
, t(
y
)
, t(
z
)
зависит от механических свойств пресса и достаточно громоздок. Явно выписывать эти функции нет необходимости
Действия 1-3 (переналадка с i-того отверстия j-тое) происходит одновременно, и пробивка происходит немедленно после завершения самого длительного из этих действий. Поэтому
С[i,j] = max(t(
x
)
, t(
y
)
, t(
z
)
)
Теперь, как и в предыдущем случае, задача составления оптимальной программы для дыропробивного пресса сводится к ЗК (здесь - симметричной).
3 АЛГОРИТМ МЕТОДА ВЕТВЕЙ И ГРАНИЦ
Запишем алгоритм:
1. Положим k == 1.
2. Осуществим приведение матрицы С по строкам и столбцам образуя приведенную матрицу Сk
.
3. Вычислим сумму приводящих констант h(
k
)
—это оценка для множества X, обозначим ее 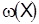 . .
4. Выберем претендентов для включении и множество Y, т. е. все те (i,j), i=1. 2, ..., j==1, 2, ..., 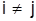 , для которых , для которых 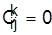 . .
5. Для выделенных претендентов на включение в Y подсчитаем:
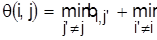 . .
6. Выберем 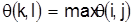 по всем i,j, у которых по всем i,j, у которых  . Пара (k,l) включается в множество Y и является запретной для множества . Пара (k,l) включается в множество Y и является запретной для множества 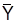 . .
7. Подсчитаем оценку для множества Y, она равна ранее произведенным затратам для множества Х и 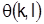 , т. е. , т. е.
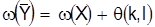 . .
8. Так как из каждого города можно выезжать только один раз, то естественно k-ю строку из дальнейшего рассмотрения исключить Так как в каждый город можно въезжать только один раз, то l-й столбец исключается.
Чтобы избежать образования замкнутых подциклов, естественно запретить переезд из l в k, т. е. клетку (l,k).
9. Полученная усеченная матрица на некотором шаге ветвления становится размерности 2х2 и содержит, очевидно, лишь две допустимые пары городов. Эти пары являются замыкающими для некоторого маршрута без петель.
Итак, момент образования матрицы 2х2 является особым, поэтому в п.9 проверяем, имеет ли полученная усеченная матрица размерность 2х2. Если «да», то переходим к п. 11. Если «нет», то к п. 10.
10. Является ли полученная матрица приведенной? Если «да», то оценка для множества Y равна оценке того множества, из которого Yполучено, т. е. 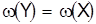 . Если «нет», то осуществляется приведение только что полученной матрицы и подсчитывается . Если «нет», то осуществляется приведение только что полученной матрицы и подсчитывается 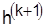 , после чего , после чего
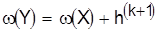 , , 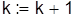
и переходим к п. 4.
11. Проверка условия оптимальности: если оценка замкнутого цикла не больше оценок всех допустимых для дальнейшего ветвления (концевых на ветвях) множеств, то полученный замкнутый маршрут является оптимальным. Если существует хотя бы одно множество с меньшей оценкой, то полученный замкнутый маршрут запоминается. Тогда процесс ветвления должен быть продолжен, исходя из множества с меньшей оценкой.
Блок-схема метода приведена на рисунке 3. Некоторые замечания: блок «матрица 2х2» определяет момент получения замыкающих пар городов для образования замкнутого маршрута; к блоку «восстановление» осуществляется переход и том случае, когда перспективным для дальнейшего ветвления оказалось множество, принадлежащее к совокупности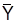 . В этом случае процесс выбора претендентов для дальнейшего ветвления требует восстановления исходной матрицы С. подсчета затрат q, необходимых для выполнение ранее построенного маршрута для множества Х, из которого . В этом случае процесс выбора претендентов для дальнейшего ветвления требует восстановления исходной матрицы С. подсчета затрат q, необходимых для выполнение ранее построенного маршрута для множества Х, из которого 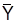 построено, т. е. построено, т. е.
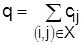 . .
После этого необходимо вычеркнуть строки и столбцы для пар, входящих в Х (аналогично п. 8), и привести полученную матрицу для выбора претендентов для ветвления.
4 РЕШЕНИЕ ПОСТАВЛЕННОЙ ЗАДАЧИ
4.1 Условие задачи
Задача
Определить оптимальную последовательность запуска деталей в производство, если задана матрица затрат на переналадку оборудования:
| № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
∞ |
21 |
11 |
18 |
8 |
15 |
9 |
| 2 |
19 |
∞ |
8 |
3 |
7 |
15 |
25 |
| 3 |
13 |
18 |
∞ |
16 |
1 |
13 |
20 |
| 4 |
16 |
5 |
14 |
∞ |
26 |
14 |
17 |
| 5 |
17 |
9 |
5 |
6 |
∞ |
12 |
19 |
| 6 |
19 |
7 |
21 |
13 |
24 |
∞ |
21 |
| 7 |
10 |
29 |
25 |
11 |
14 |
17 |
∞ |
Сделать анализ решенной задачи.
ВЫВОДЫ
В результате выполненной работы были изичуны эврестический, приближенный и точный алгоритмы решения задач коммивояжера. Точные алгоритмы решения задач коммивояжера – это полный перебор или усовершенствованный перебор. Оба они, особенно первый, не эффективны при большом числе вершин графа.
Для малого числа вершин наиболее эффективный точный метод лексического перебора, для большого числа вершин рациональнее применять метод ветвей и границ. Изучены практические применения задач коммиявожера и задачи n станков.
Особенно рассмотрен метод ветвей и границ в задачах коммивояжера. Приведен алгоритм данного метода, схема алгоритма, а также решена задача на определение оптимальной последовательности запуска деталей в производство, если задана матрица затрат на переналадку оборудования. После чего был произведен анализ решенной задачи.
Также прилагается программана решающая задачу о коммивояжере методом ветвей и границ. Для разработки данной программы была использованя среда разработки Delphi версии 6.0.
Delphi 6.0 представляет собой уникальную систему разработки, в которой технология высокопроизводительной оптимизмпующей компиляции сочетается с визуальными средствами разработки и масштабируемым процессом баз данных.
Данная программа решает задачи разной размерности, что доказывает её универсальность для любых задач данного типа.
ЛИТЕРАТУРА:
1 Балашевич В.А., Алгоритмизация математических методов планирования и управления. - Минск: Вышэйшая школа,1979.-286с
2 Дегтярев Ю.И., Исследование операций.- Москва: Высшая школа,1986.-270с.
3 Ляшенко И.Н. Линейное и нелинейное программирование – Киев: Вища школа,1975.-370с.
ПРИЛОЖЕНИЕ А
(обязательное)
Текст программы
Схема программы
Описание программы
Инструкция пользователю
ПРИЛОЖЕНИЕ Б
(обязательное)
Входная информация
ПРИЛОЖЕНИЕ В
(обязательное)
Выходная информация
|