1 Постановка задач линейного программирования (ЗЛП). Примеры экономических задач, сводящихся к ЗЛП. Допустимые и оптимальные решения
2 Алгоритм Флойда. Постановка задачи
1 Постановка задач линейного программирования (ЗЛП). Примеры экономических задач, сводящихся к ЗЛП. Допустимые и оптимальные решения
В общем виде задача линейного программирования (в дальнейшем ЗЛП) может быть сформулирована как задача нахождения наибольшего значения линейной функции
 (1) (1)
на некотором множестве DÌRn
,где xÎDудовлетворяют системе ограничений




 (2) (2)
и, возможно, ограничениям
 (3) (3)
He умаляя общности, можно считать, что в системе (2) первые т ограничений являются неравенствами, а последующие — l-уравнениями. Очевидно, этого всегда можно добиться за счет простого переупорядочения ограничений. Относительно направления знака неравенства будем предполагать, что левая часть меньше или равна правой. Добиться этого можно, умножив на (-1) обе части тех неравенств, которые имеют противоположный знак. Ограничения (3), вообще говоря, могут быть рассмотрены как частный случай ограничений в форме неравенств, но в силу особой структуры их обычно выделяют отдельно и называют условиями неотрицательности (или тривиальными ограничениями).
Дополнительно следует заметить, что выбор типа искомого экстремума (максимума или минимума) также носит относительный характер. Так, задача поиска максимума функции

эквивалентна задаче поиска минимума функции

Часто условия задачи (1) - (3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращенной матричной форме

где с и x — векторы из пространства Rn
, b — вектор из пространства Rm
, a А — матрица размерности m´ п.
Задачу линейного программирования, записанную в форме (1) - (3), называют общей задачей линейного программирования (ОЗЛП).
Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные xj
наложены условия неотрицательности, то она называется задачей линейного программирования в канонической форме, или канонической задачей линейного программирования (КЗЛП). В матричной форме КЗЛП можно записать в следующем виде:

Поскольку любая оптимизационная задача однозначно определяется целевой функцией f и областью D, на которой отыскивается оптимум (максимум), будем обозначать эту задачу парой (D, f).
Условимся относительно терминологии, которая используется в дальнейшем и является общепринятой в теории линейного программирования.
Планом ЗЛП называется всякий вектор х из пространства Rn
.
Допустимым планом называется такой план ЗЛП, который удовлетворяет ограничениям (1.2)-(1.3), т. е. содержится в области D. Сама область Dназывается при этом областью допустимых планов. Оптимальным планом х*
называется такой допустимый план, при котором целевая функция достигает оптимального (в нашем случае — максимального) значения, т. е. план, удовлетворяющий условию
maxf(x) = f(x*
).
Величина f*
= f(x*
) называется оптимальным значением целевой функции.
Решением задачи называется пара (х*
, f*
), состоящая из оптимального плана и оптимального значения целевой функции, а процесс решения заключается в отыскании множества всех решений ЗЛП.
Примеры экономических задач, сводящихся к ЗЛП.
Несмотря на многообразие задач математического программирования, при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое операционное исследование. Как правило, это:
1.Постановка задачи.
2.Построение содержательной (вербальной) модели рассматриваемого объекта (процесса). На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.
3.Построение математической модели, т. е. перевод сконструированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.
4.Решение задач, сформулированных на базе построенной математической модели.
5.Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная корректировка первоначальной модели.
6.Реализация полученного решения на практике.
Математическое моделирование в исследовании операций является, с одной стороны, очень важным и сложным, а с другой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся попытки выделить общие принципы создания математических моделей приводили либо к декларированию рекомендаций самого общего характера, трудноприложимых для решения конкретных проблем, либо, наоборот, к появлению рецептов, применимых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой математического моделирования на конкретных примерах.
В качестве таких примеров приведем несколько классических экономико-математических моделей и задач, которые могут быть сформулированы на их основе.
Управление портфелем активов.
Рассмотрим проблему принятия инвестором решения о вложении имеющегося у него капитала. Набор характеристик потенциальных объектов для инвестирования, имеющих условные имена от А до F, задается следующей таблицей.
| Название |
Доходность (в %) |
Срок выкупа (год) |
Надежность (в баллах) |
| А |
5,5 |
2001 |
5 |
| В |
6,0 |
2005 |
4 |
| С |
8,0 |
2010 |
2 |
| D |
7,5 |
2002 |
3 |
| Е |
5,5 |
2000 |
5 |
| F |
7,0 |
2003 |
4 |
Предположим, что при принятии решения о приобретении активов должны быть соблюдены условия:
a.суммарный объем капитала, который должен быть вложен, составляет $ 100 000;
b.доля средств, вложенная в один объект, не может превышать четверти от всего объема;
c.более половины всех средств должны быть вложены в долгосрочные активы (допустим, на рассматриваемый момент к таковым относятся активы со сроком погашения после 2004 г.);
d.доля активов, имеющих надежность менее чем 4 балла, не может превышать трети от суммарного объема.
Приступим к составлению экономико-математической модели для данной ситуации. Целесообразно начать процесс с определения структуры управляемых переменных. В рассматриваемом примере в качестве таких переменных выступают объемы средств, вложенные в активы той или иной фирмы. Обозначим их как хА
, хВ
, хС
, хD
, хE
, хF
. Тогда суммарная прибыль от размещенных активов, которую получит инвестор, может быть представлена в виде
 (1) (1)
На следующем этапе моделирования мы должны формально описать перечисленные выше ограничения a-d на структуру портфеля.
a) Ограничение на суммарный объем активов:
xA
+ xB
+ xС
+ xD
+ xE
+ xF
£100 000. (2)
b) Ограничение на размер доли каждого актива:
хА
£25 000, хВ
£25 000, хС
£ 25 000,
xd
£ 25 000, хе
£ 25 000, xf
£25 000. (3)
c) Ограничение, связанное с необходимостью вкладывать половину средств в долгосрочные активы:
хВ
+ хС
³ 50 000 (4)
d) Ограничение на долю ненадежных активов:
xC
+ xD
£ 30 000. (5)
Наконец, система ограничений в соответствии с экономическим смыслом задачи должна быть дополнена условиями неотрицательности для искомых переменных:
хА
³ 0, хB
³0, хC
³ 0, xD
³0, хЕ
³0, xF
³ 0. (6)
Выражения (1)-(6) образуют математическую модель поведения инвестора. В рамках этой модели может быть поставлена задача поиска таких значений переменных ха
, хB
, хC
, xd
, xe
, хF
, при которых достигается наибольшее значение прибыли (т. е. функции (1)) и одновременно выполняются ограничения на структуру портфеля активов (2)-(6).
Перейдем теперь к рассмотрению более общих моделей и задач.
Простейшая задача производственного планирования.
Пусть имеется некоторый экономический объект (предприятие, цех, артель и т. п.), который может производить некоторую продукцию п видов. В процессе производства допустимо использование т видов ресурсов (сырья). Применяемые технологии характеризуются нормами затрат единицы сырья на единицу производимого продукта. Обозначим через ai
,
j
количество i-го ресурса (iÎ1: m), которое тратится на производство единицы j-го продукта (jÎ1:n). Весь набор технологических затрат в производстве j-го продукта можно представить в виде вектора-столбца

а технологию рассматриваемого предприятия (объекта) в виде прямоугольной матрицы размерности т на п:
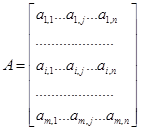
Если j-й продукт производится в количестве xj
, то в рамках описанных выше технологий мы должны потратить a1,
j
xj
первого ресурса, a2,
j
xj
— второго, и так далее, amj
xj
— т-го. Сводный план производства по всем продуктам может быть представлен в виде n-мерного вектора-строки x = (x1,
x2
,...,xj
,...,xn
) . Тогда общие затраты по i-му ресурсу на производство всех продуктов можно выразить в виде суммы

представляющей собой скалярное произведение векторов аj
и х. Очевидно, что всякая реальная производственная система имеет ограничения на ресурсы, которые она тратит в процессе производства. В рамках излагаемой модели эти ограничения порождаются m-мерным вектором b = (b1,
b2
,...,bm
), где bi
— максимальное количество i-го ресурса, которое можно потратить в производственном процессе. В математической форме данные ограничения представляются в виде системы т неравенств:
a1,1
xl
+al,2
x2
+...+al,n
xn
£ bl
,
o2,l
xl
+a2,2
x2
+...+a2,n
xn
£ b2
,
am
,l
xl
+am,2
x2
+...+am,n
xn
£ bn
.(7)
Применяя правила матричной алгебры, систему (7) можно записать в краткой форме, представив левую часть как произведение матрицы А на вектор х, а правую — как вектор b:
Ах £ b. (8)
К системе (8) также должны быть добавлены естественные ограничения на неотрицательность компонентов плана производства: x1
, ³ 0,..., xj
³0, ..., хп
³0, или, что то же самое,
x³ 0. (9)
Обозначив через сj
цену единицы j-го продукта, получим выражение суммарного дохода от выполнения плана производства, задаваемого вектором х:
 (10) (10)
Формулы (8)-(10) являются не чем иным, как простейшей математической моделью, описывающей отдельные стороны функционирования некоторого экономического объекта, поведением которого мы хотим управлять. В рамках данной модели, вообще говоря, можно поставить различные задачи, но, скорее всего, самой «естественной» будет задача поиска такого плана производства xÎRn
, который дает наибольшее значение суммарного дохода, т. е. функции (10), и одновременно удовлетворяет системе ограничений (8)-(9). Кратко такую задачу можно записать в следующем виде:
 где где  (11) (11)
Несмотря на явную условность рассматриваемой ситуации и кажущуюся простоту задачи (11), ее решение является далеко не тривиальным и во многом стало практически возможным только после разработки специального математического аппарата. Существенным достоинством используемых здесь методов решения является их универсальность, поскольку к модели (11) могут быть сведены очень многие как экономические, так и неэкономические проблемы.
Поскольку любая научная модель содержит упрощающие предпосылки, для корректного применения полученных с ее помощью результатов необходимо четкое понимание сути этих упрощений, что, в конечном счете, и позволяет сделать вывод об их допустимости или недопустимости. Наиболее «сильным» упрощением в рассмотренной модели является предположение о прямо пропорциональной (линейной) зависимости между объемами расхода ресурсов и объемами производства, которая задается с помощью норм затрат аi
,
j
. Очевидно, что это допущение далеко не всегда выполняется. Так, объемы расхода многих ресурсов (например, основных фондов) изменяются скачкообразно в зависимости от изменения компонентов объема производства х. К другим упрощающим предпосылкам относятся предположения о независимости цен сj
от объемов хj
, что справедливо лишь для определенных пределов их изменения, пренебрежение эффектом кооперации в технологиях и т. п. Данные «уязвимые» места важно знать еще и потому, что они указывают принципиальные направления совершенствования модели.
2
Алгоритм Флой
д
а. Постановка задачи
Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i, j) равен расстоянию dij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае.
Основная идея метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними (рис. 1). Если выполняется неравенство dij + djk < dik, то целесообразно заменить путь i -> k путем i -> j -> k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.
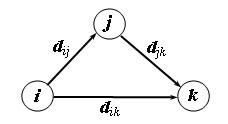
Рис.1. Треугольный оператор
Определяем начальную матрицу расстояния D0 и матрицу последовательности узлов S0. Диагональные элементы обеих матриц помечаются знаком "-", показывающим, что эти элементы в вычислениях не участвуют. Полагаем k = 1:
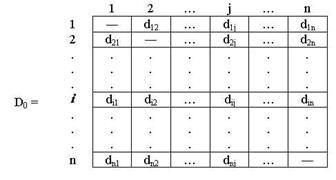
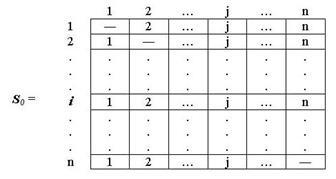
Рис.2. Начальная ситуация
Основной шаг k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементам dij матрицы Dk-1. Если выполняется неравенство dik + dkj < dij, (i <> k, j <> k, i <> j), тогда выполняем следующие действия:
создаем матрицу Dk путем замены в матрице Dk-1 элемента dij на сумму dik + dkj,
создаем матрицу Sk путем замены в матрице Sk-1 элемента sij на k. Полагаем k = k + 1 и повторяем шаг k.
Поясним действия, выполняемые на k-м шаге алгоритма, представив матрицу Dk-1 так, как она показана на рисунке 3. На этом рисунке строка k и столбец k являются ведущими. Строка i - любая строка с номером от 1 до k - 1, а строка p - произвольная строка с номером от k + 1 до n. Аналогично столбец j представляет любой столбец с номером от 1 до k - 1, столбец q - произвольный столбец с номером от k + 1 до n. Треугольный оператор выполняется следующим образом. Если сумма элементов ведущих строки и столбца (показанных в квадратах) меньше элементов, находящихся в пересечении столбца и строки (показанных в кружках), соответствующих рассматриваемым ведущим элементам, то расстояние (элемент в кружке) заменяется на сумму расстояний, представленных ведущими элементами:
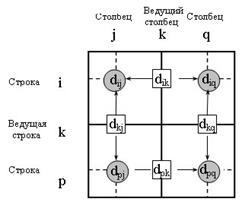
Рис.3. Иллюстрация алгоритма Флойда
После реализации n шагов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам.
Расстояние между узлами i и j равно элементу dij в матрице Dn.
Промежуточные узлы пути от узла i к узлу j определяем по матрице Sn. Пусть sij = k, тогда имеем путь i -> k -> j. Если далее sik = k и skj = j, тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла i к узлу k и от узла k к узлу j.
Пример. Найдем для сети, показанной на рисунке 4, кратчайшие пути между любыми двумя узлами. Расстояние между узлами этой сети проставлены на рисунке возле соответствующих ребер. Ребро (3, 5) ориентированно, поэтому не допускается движение от узла 5 к узлу 3. Все остальные ребра допускают движение в обе стороны:
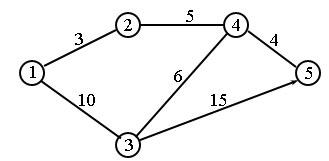
Рис.4. Пример сети
Начальные матрицы D0 и S0 строятся непосредственно по заданной схеме сети. Матрица D0 симметрична, за исключением пары элементов d35 и d53, где d53 равно бесконечности, поскольку невозможен переход от узла 5 к узлу 3:
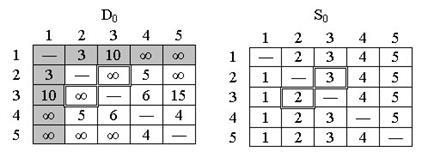
Рис.5. Начальное состояние
В матрице D0 выделены ведущие строка и столбец (k = 1). Двойной рамкой представлены элементы d23 и d32, единственные среди элементов матрицы D0, значения которых можно улучшить с помощью треугольного оператора. Таким образом, чтобы на основе матриц D0 и S0 получить матрицы D1 и S1, выполняем следующие действия.
Заменяем d23 на d21 + d13 = 3 + 10 = 13 и устанавливаем s23 = 1.
Заменяем d32 на d31 + d12 = 10 + 3 = 13 и устанавливаем s32 = 1.
Матрицы D1 и S1 имеют следующий вид:
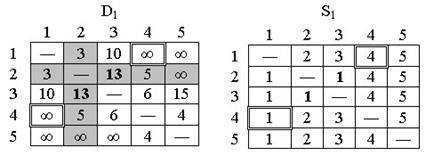
Рис.6. Матрицы D1 и S1
Полагаем k = 2; в матрице D1 выделены ведущие строка и столбец. Треугольный оператор применяется к элементам матрицы D1 и S1, выделенным двойной рамкой.
В результате получаем матрицы D2 и S2:
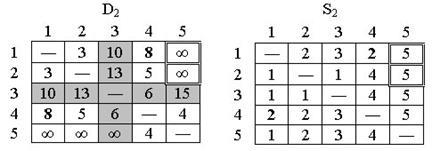
Рис.7. Матрицы D2 и S2
Полагаем k = 3; в матрице D2 выделены ведущие строка и столбец. Треугольный оператор применяется к элементам матрицы D2 и S2, выделенным двойной рамкой. В результате получаем матрицы D3 и S3:
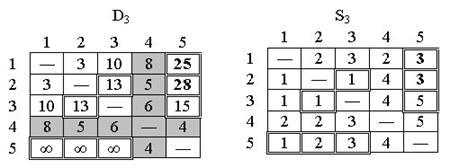
Рис.8. Матрицы D3 и S3
Полагаем k = 4, ведущие строка и столбец в матрице D3 выделены. Получаем новые матрицы D4 и S4:
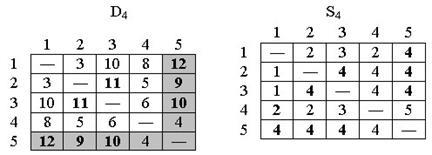
Рис.9. Матрицы D4 и S4
Полагаем k = 5, ведущие строка и столбец в матрице D4 выделены. Никаких действий на этом шаге не выполняем; вычисления закончены.
Конечные матрицы D4 и S4 содержат всю информацию, необходимую для определения кратчайших путей между любыми двумя узлами сети. Например, кратчайшее расстояние между узлами 1 и 5 равно d15 = 12.
Для нахождения соответствующих маршрутов напомним, что сегмент маршрута (i, j) состоит из ребра (i, j) только в том случае, когда sij = j. В противном случае узлы i и j связаны, по крайней мере, через один промежуточный узел. Например, поскольку s15 = 4 и s45 = 5, сначала кратчайший маршрут между узлами 1 и 5 будет иметь вид 1->4->5. Но так как s14 не равно 4, узлы 1 и 4 в определенном пути не связаны одним ребром (но в исходной сети они могут быть связаны непосредственно). Далее следует определить промежуточный узел (узлы) между первым и четвертым узлами. Имеем s14 = 2 и s24 = 4, поэтому маршрут 1->4 заменяем 1->2->4. Поскольку s12 = 2 и s24 = 4, других промежуточных узлов нет. Комбинируя определенные сегменты маршрута, окончательно получаем следующий кратчайший путь от узла 1 до узла 5: 1->2->4->5. Длина этого пути равна 12 километрам.
1. Ляшенко И.Н. Линейное и нелинейное программирование. Киев, 1975г.
2. Моисеев Н.Н. Математические задачи системного анализа. Москва, 1981г.
3. Крушевский А.В. Справочник по экономико-математическим моделям и методам. Киев, 1982г.
|