БЕЛОРУССКИЙ ГОСУДРАСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра инженерной графики
РЕФЕРАТ
На тему:
«Передаточное отношение многоступенчатых передач»
МИНСК, 2008
В простой зубчатой передаче, состоящей из двух находящихся в зацеплении колес, при внешнем зацеплении колеса вращаются в разные стороны, поэтому передаточное отношение (3.6) отрицательное, а в передаче с внутренним зацеплением передаточное отношение положительное, т.е.
i12
= ω1
/ω2
= ±z2
/z1
, (1)
где знак «–» принимают при внешнем зацеплении колес, знак «+» – при внутреннем.
 Передаточное отношение, которое можно воспроизвести одной парой зубчатых колес (исключая червячную передачу) невелико, так как минимальное и максимальное значения чисел зубьев колес ограничены и лимитируются определенными технологическими факторами. При необходимости получения больших передаточных отношений применяют сложные зубчатые механизмы, состоящие из нескольких простых цилиндрических, конических, червячных зубчатых механизмов, соединенных
Передаточное отношение, которое можно воспроизвести одной парой зубчатых колес (исключая червячную передачу) невелико, так как минимальное и максимальное значения чисел зубьев колес ограничены и лимитируются определенными технологическими факторами. При необходимости получения больших передаточных отношений применяют сложные зубчатые механизмы, состоящие из нескольких простых цилиндрических, конических, червячных зубчатых механизмов, соединенных последовательно, т.е. применяют многоступенчатую передачу. Передача вращающего момента осуществляется последовательно с одного вала на другой через зубчатые колеса, причем на каждом промежуточном валу размещают по два колеса, одно из которых является ведомым по отношению к предыдущему, другое – ведущим по отношению к последующему.
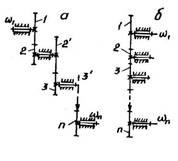
Рассмотрим плоский ступенчатый зубчатый механизм (рис. 1, а), представляющий собой последовательное соединение нескольких простых механизмов. На каждом промежуточном валу находится не менее двух колес, зацепляющихся соответственно с колесами предыдущего и последующего валов. Ведущим является колесо 1, общее передаточное отношение всего механизма i1n = ω1/ωn, где ω1, ωn – соответственно скорости вращения ведущего и выходного n-го звена. Выразим, пользуясь зависимостью, передаточные отношения простых механизмов, состоящих из одной пары колес, находящихся в зацеплении i12
= ω1
/ω2
= –z2
/z1
; i23
= ω2
/ω3
= –z3
/z2'
и т.д. Перемножим полученные соотношения i12
∙i23
∙…∙i(n–1)n
= (ω1
/ω2
)∙(ω2
/ω3)∙…´
´ (ωn–1/ωn) = ω1/ωn, но ω1/ωn = i1n, поэтому
i1n = i12∙i23
∙…∙i(n–1)n, (2)
т.е. передаточное отношение многоступенчатой передачи равно произведению передаточных отношений всех простых зубчатых передач, входящих в механизм. Зависимость можно выразить через числа зубьев колес. Для схемы, представленной на рис. 1, а, она примет вид:
i1n = (–1)k(z2
/z1
)∙(z3
/z2'
)∙…∙(zn
/z(n–1)'
),
где z1
, z2'
, …, zn
– числа зубьев колес передачи; k – число внешних зацеплений. Множитель (–1)k позволяет определить знак передаточного отношения сложного многоступенчатого механизма, т.е. направление вращения выходного звена по отношению к направлению вращения ведущего.
При передаче движения с малым передаточным отношением между валами, находящимися на большом расстоянии друг от друга для уменьшения габаритов передачи или для получения требуемого направления вращения выходного звена применяют последовательное соединение нескольких пар единичных зубчатых колес (рис. 1, б), так называемые рядовые зубчатые механизмы. Полное передаточное отношение такой передачи (1) через известные числа зубьев колес равно i1n = ω1
/ωn
= (–1)k(zn
/z1
), где z1
, zn
– числа зубьев ведущего и выходного колес. Промежуточные колеса влияют только на знак, но не величину передаточного отношения механизма, их называют паразитными.
Когда необходимо передавать движение между пересекающимися или между скрещивающимися осями, используют пространственные многозвенные зубчатые механизмы с применением конических или червячных передач.
Кулачковые механизмышироко применяются в устройствах управления, прерывистого движения.
Простейший кулачковый механизм (рис. 2, а) состоит из кулачка 1, толкателя 2 и стойки, образуя в точке А высшую кинематическую пару 4-го класса. Ведущее звено 1 называется кулачком или эксцентриком. Форма профиля кулачка определяется законом движения толкателя и может быть самой разнообразной, как и закон движения ведомого звена. Кулачковые механизмы позволяют получать любой закон движения ведомого звена, отличаются своей простотой и компактностью, малыми габаритами.
К недостаткам кулачковых механизмов следует отнести большие удельные давления в высшей паре, и следовательно, недолговечность механизма, а также необходимость в силовом замыкании звеньев. Возможно геометрическое замыкание с помощью пазов в кулачке, который направляет движение ведомого звена.
Величина перемещений или закон движения рабочего звена механизма определяется профилем кулачка.

 Рис. 2
По виду преобразуемых движений кулачковые механизмы можно разделить на следующие группы: механизмы, в которых вращательное движение кулачка 1 преобразуется в возвратно-поступательное или качательное движение толкателя 2 (см. соответственно рис. 2, а, б); механизмы, в которых возвратно-поступательное движение кулачка 1 преобразуется в возвратно-поступательное или качательное движение толкателя 2 (см. соответственно рис. 2, в, г); пространственные или коноидные кулачковые механизмы, решающие функции двух переменных, например, φ2
= φ2
(x, φ) (см. рис. 2, д). Эти механизмы имеют две степени свободы. Применяются они в передающих устройствах.
Толкатели кулачковых механизмов в зависимости от вида кинематического элемента толкателя подразделяются на: точечные (см. рис. 2, д), плоские и тарельчатые (см. рис. 2, а), с профилем, очерченным по радиусу или сфере (см. рис. 3.9, д), роликовые или шариковые (см. соответственно рис. 2, в, г).
Механизмы винт – гайкаиспользуются для преобразования вращательного движения в поступательное. Для преобразования поступательного движения во вращательное эти механизмы используются редко (механизм перемещения пленки фотоаппарата).
Достоинствами таких механизмов являются высокая точность и плавность поступательного перемещения, простота конструкции и изготовления, компактность, надежность в работе, возможности получения самотормозящей передачи и создания значительных усилий при малых перемещениях. Недостатки механизмов винт – гайка – большие потери на трение в винтовой паре, что обуславливает низкий КПД и повышенный износ.
Механизмы винт – гайка применяют для перемещения магнитных и оптических головок считывания и записи информации в дисководах ПЭВМ; перемещения координатных столов технологического оборудования при изготовлении полупроводниковых и электронных приборов; настройки волноводов; фокусировки окуляров и объективов: перемещения кареток и суппортов станков; измерительных и регулировочных устройств; рабочих органов роботов, испытательных машин и т.д.
Основными элементами механизмов винт – гайка являются винт 1 и гайка 2 (рис. 3, а). Материалы винта и гайки должны обладать низким коэффициентом трения, высокой износостойкостью и хорошо обрабатываться.
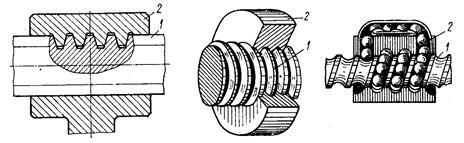
Винт представляет собой цилиндр, на части которого нарезана резьба. Изготавливают винты обычно из сталей 45 и 50, а в кинематических передачах– из пластмасс. Гайка представляет собой втулку или корпус с резьбой в отверстии. Для уменьшения трения скольжения (рис. 3, б) гайки изготавливают из пластмасс, оловянистых бронз типа БрОЦС 6-6-3, латуни Л60 … 62. С целью уменьшения потерь на трение применяют механизмы винт – гайка с трением качения (рис. 3, в). В этой более сложной конструкции резьба заменена винтовыми канавками кругового профиля. Канавки на винте и гайке образуют замкнутую винтовую поверхность, ограничивающую полость, в которую помещаются шарики. Контакт между винтом и гайкой осуществляется посредством шариков. При вращении винта шарики увлекаются в направлении его поступательного движения, попадают в отводной канал в гайке и снова возвращаются в полость между винтом и гайкой.
Простейшие винтовые механизмы могут состоять из двух и трех звеньев. Наибольшее распространение получили трехзвенные схемы. Рассмотрим возможные кинематические схемы винтовых механизмов (рис. 4):
двухзвенный механизм (рис. 4, а). Винт 1 вращается и одновременно движется поступательно, гайка 2 неподвижна. Механизмы с такой схемой обладают наибольшей точностью получения линейных перемещений при ограниченной величине этих перемещений (до 50 мм). Применяют эту схему в измерительных устройствах (микрометры), механизмах настройки волноводов;
– трехзвенный механизм (рис. 4, б). Ведущий винт 1 образует со стойкой вращательную пару и винтовую пару с гайкой 2, которая движется поступательно по неподвижным направляющим. Механизмы с такой схемой обладают меньшей точностью, но значительным линейным перемещением гайки. Используют их для перемещения координатных столов технологического оборудования при изготовлении полупроводниковых приборов и для перемещения магнитных и оптических головок в дисководах ПЭВМ;
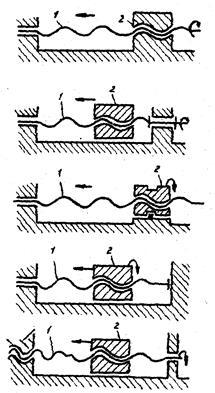
Рис. 4 трехзвенный механизм (рис. 4, в). Ведущим звеном является зафиксированная в осевом направлении вращающаяся гайка 2. Ведомое звено – винт 1 образует со стойкой поступательную кинематическую пару. Механизмы с такой кинематической схемой используются для получения сравнительно грубых установочных перемещений (установка на резкость окуляра бинокля);
двухзвенный механизм (рис. 4, г). Гайка 2 вращается и движется поступательно, винт 1 является стойкой, неподвижен. Механизмы с такой кинематической схемой используют в устройствах для получения сравнительно грубых установочных перемещений;
– трехзвенный механизм с двумя разными резьбами на винте (рис. 4, д) позволяет получать за один оборот винта 1 относительно малые перемещения ведомой гайки 2. Винт 1 вращается и движется поступательно относительно стойки-гайки 3, гайка 2 перемещается поступательно относительно направляющих. Механизм называется дифференциальным и применяется для получения перемещений, равных разности ходов винта в стойке 3 и гайки 2.
В механизмах винт – гайка с трением скольжения резьба нанесена непосредственно на детали винтовой пары. Характеризуется резьба следующими геометрическими параметрами (рис. 5): d – наружный диаметр резьбы; d1
– внутренний диаметр резьбы; d2
– средний диаметр резьбы; р – шаг резьбы–расстояние, измеренное вдоль оси резьбы, между параллельными сторонами соседних витков; рh
–ход резьбы, для однозаходной рh
= р, а для многозаходной – рh
= zр, где z – число заходов; h – рабочая высота профиля; a – угол профиля; g – угол подъема резьбы (рис. 5) образован касательной к винтовой линии в точке на среднем диаметре резьбы и плоскостью, перпендикулярной к оси резьбы, и определяется из выражения
tg g = z p/p d2
. (3)
Геометрические параметры резьб и допуски на их размеры стандартизированы. Резьбы классифицируют по различным признакам:
по форме поверхности, на которую наносится резьба – на цилиндрическую и коническую. Наиболее распространена цилиндрическая резьба. Коническую резьбу применяют для плотных соединений пробок, труб;
по форме профиля – на треугольные, трапецеидальные, прямоугольные, круглые и др.;
по направлению винтовой линии – на правую и левую резьбу. Винты с правой резьбой ввинчивают по часовой и вывинчивают против часовой стрелки. Правое направление имеет абсолютное большинство резьб.
По назначению резьбы делят на крепежные, крепежно-уплотнительные и ходовые. Крепежная резьба должна обладать достаточной прочностью и значительным трением, предохраняющим соединяемые детали от самоотвинчивания. Крепежно-уплотнительные резьбы помимо перечисленных свойств должны обеспечить повышенную плотность соединения. Ходовые резьбы должны быть с малым трением, чтобы уменьшить износ и повысить КПД подвижного резьбового соединения.
Метрическая резьба (см. рис. 5, а) получила наибольшее распространение в резьбовых крепежных соединениях. Имеет профиль равностороннего треугольника с углом профиля a = 60°. Вершины и впадины резьбы для уменьшения концентрации напряжений притуплены по прямой или по дуге. Радиальный зазор в резьбе делает ее негерметичной. Метрические резьбы делятся на резьбы с крупным (основным) и мелким шагом. Резьбы с мелким шагом меньше ослабляют деталь, обладают более высокой динамической прочностью и характеризуются из-за малого угла подъема g винтовой линии повышенным самоторможением. Как крепежные, резьбы с мелким шагом применяются в соединениях, подверженных переменным воздействиям и в тонкостенных деталях. Метрическая резьба обеспечивает лучшее направление винта или гайки в винтовых механизмах из-за малого радиального смещения по сравнению с трапецеидальной резьбой. В механизмах винт-гайка с шагами резьбы до 1 мм применяют только метрические резьбы из-за сложности изготовления с такими шагами ходовых резьб трапецеидального и прямоугольного профилей.
Дюймовая резьба используется для крепежных деталей импортного оборудования, вышедших из строя. Она имеет угол профиля a = 55° и плоскосрезанные вершины треугольного профиля. Параметры резьбы дают в дюймах [один дюйм 1² = 25,4 мм]. Применение дюймовых резьб (кроме трубных) для новых изделий запрещается.
 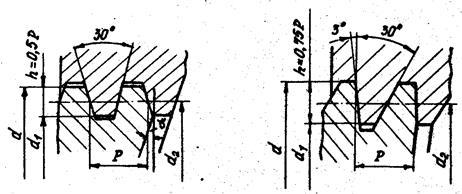
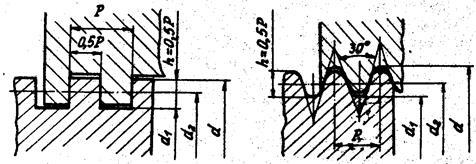 Рис. 5
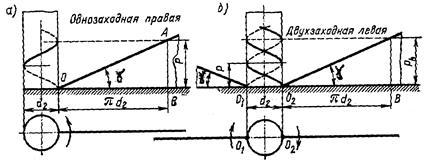 Рис. 6
Трубная резьба представляет собой мелкую дюймовую резьбу, она обеспечивает беззазорность и плотность резьбового соединения за счет скругления вершин и впадин резьбы (см. рис. 5, б). За номинальный диаметр трубной резьбы принимают внутренний диаметр трубы, а наружный диаметр трубной резьбы больше номинального на величину удвоенной толщины стенки трубы. Например, резьба труб ½ ² используется для труб с внутренним диаметром ½ ², наружный диаметр ее равен 20,96 мм. Используется трубная резьба в трубопроводах и для тонкостенных деталей.
Трапецеидальная резьба (см. рис. 5, в) – основная резьба в механизмах винт-гайка. Ее профиль – равнобокая трапеция с углом a = 30°. Резьба имеет меньшие по сравнению с резьбой треугольного профиля потери на трение, больший КПД, обеспечивает высокую точность осевого перемещения ведомого звена. Широко применяется для реверсивных передач винт-гайка.
Упорная резьба (см. рис. 5, г) имеет профиль неравнобокой трапеции с углом a = 30°. Рабочая сторона профиля имеет угол наклона 3°, КПД этой резьбы выше, чем КПД трапецеидальной резьбы. Рекомендуется применять эту резьбу в механизмах винт-гайка при значительных односторонних осевых нагрузках.
Прямоугольная резьба (см. рис. 5, д) с профилем в форме квадрата имеет самый высокий КПД, так как угол профиля резьбы a = 0. Резьба обладает пониженной прочностью. При износе образуются осевые зазоры, которые трудно устранить. Резьба применяется в малонагруженных передачах винт-гайка (перемещение головок записи и считывания информации в дисководах).
Круглая резьба (см. рис. 5, е) имеет угол профиля a = 30°. Профиль резьбы состоит из дуг, сопряженных короткими прямыми линиями. Резьба не стандартизирована. Характеризуется высокой динамической прочностью, имеет ограниченное применение.
В механизмах винт-гайка применяют трапецеидальные, метрические, прямоугольные и упорные резьбы. Наибольшее применение получили трапецеидальные и метрические резьбы. Трапецеидальную резьбу рекомендуют применять с шагом р > 1 мм, метрическую в механизмах с мелкими шагами (р £ 1,0).
КПД винтовых механизмов рассчитывают по формуле
h = tgg / tg(g + rт
), (4)
где g – угол подъема винтовой линии; rт
– приведенный угол трения.
Для резьбы приведенный угол трения
rт
= arctgf¢ = arctg[f / cos(a/2)], (5)
где f¢ – приведенный коэффициент трения скольжения; f – коэффициент трения скольжения между материалами винта и гайки; a – угол профиля резьбы.
Для прямоугольной резьбы a = 0 и f¢ = f, для трапецеидальной резьбы a = 30° и f¢ = 1,04 f; для метрической резьбы a = 60° и f¢ = 1,15 f.
Наибольшим КПД обладает прямоугольная, а наименьшим – метрическая резьба.
Кинематика винтовых механизмов
В технических системах более всего распространены винтовые механизмы, выполненные по схеме, представленной на рис. 6, б. Зависимость линейного перемещения ℓ2
ведомой гайки от угла поворота j1
винта (функция положения) имеет вид
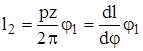 , (6) , (6)
где 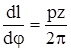 – передаточная функция, или аналог скорости передачи винт-гайка. – передаточная функция, или аналог скорости передачи винт-гайка.
Линейная скорость ведомой гайки
v2
= dl2
/dt = 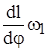 , (6) , (6)
где w1
= dj1
/dt – угловая скорость винта.
Для снижения скорости линейного перемещения гайки при заданной угловой скорости винта w1
уменьшают шаг резьбы р и число ее заходов z принимают равным 1. Скорость перемещения гайки v2
можно уменьшить за счет снижения угловой скорости винта w1
с помощью червячной или многоступенчатой зубчатой передачи (редуктора). Эти редукторы устанавливают между двигателем и передачей винт – гайка. Тогда w1
= wд
/ iд1
, где iд1
– передаточное отношение зубчатого редуктора, wд
– скорость вращения двигателя.
Механизм с дифференциальным винтом (рис. 6, д) имеет две винтовые пары с разными параметрами резьбы. В паре со стойкой 3 винт имеет резьбу с шагом р1
и числом заходов z1
, а в винтовой паре с ведомой гайкой 2 – резьбу с шагом р2
и числом заходов z2
. Аналог скорости поступательного перемещения в соответствующих винтовых парах будет соответственно равен 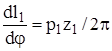 и и 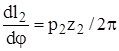 . Функция положения, т.е. зависимость линейного перемещения гайки 2 от угла поворота винта, равна . Функция положения, т.е. зависимость линейного перемещения гайки 2 от угла поворота винта, равна
 , (7) , (7)
где знак минус относится к механизмам с винтом, имеющим резьбы одного направления винтовой линии, а знак плюс – к механизмам с винтом, имеющим резьбы в парах со стойкой 3 и гайкой 2 с разным направлением винтовой линии, например, правую и левую резьбы.
Длина нарезанной части винта Lb
определяется по формуле
Lb
=ℓmax
+ℓr
+Dℓ, (8)
где ℓmax – максимальное перемещение винта или гайки; ℓr – длина резьбы гайки; Dℓ – запас резьбы (2 … 3 витка).
Для обеспечения достаточной прочности и жесткости диаметр винта d выбирают из соотношения d ³ 0,05 Lb.
Механизмы с гибкими звеньями
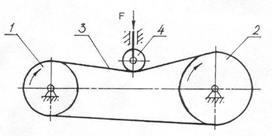
Применяют для передачи вращательного движения между валами при больших межосевых расстояниях и для преобразования вращательного движения в поступательное и наоборот. Ведущее и ведомое жесткие звенья таких механизмов не имеют между собой непосредственного контакта, а передача движения осуществляется посредством гибкого звена, которое может быть как замкнутым, так и разомкнутым. По характеру соединения гибкого звена с ведущим и ведомым звеньями рассматриваемые механизмы подразделяют на передачи трением, передачи зацепления и передачи с жестким креплением гибкого звена к другим звеньям. В передачах трением в качестве гибкого звена используют плоские и клиновидные ремни, пассики, круглые шнуры и ремни, нити (рис. 9, а). Передача состоит из ведущего 1 и ведомого 2 шкивов, а также замкнутого звена 3, надетого на шкивы с натяжением. Таким передачам присущи все достоинства и недостатки фрикционных механизмов непосредственного касания. Необходимым условием нормальной работы передачи трением является натяжение гибкого звена, что достигается обычно при помощи натяжного ролика 4 (см. рис. 9 ). В передачах зацепления гибким звеном служит зубчатый ремень, перфорированная лента, цепь. Преимущества этих передач (см. рис. 9, б) перед передачами трением соответствуют преимуществам зубчатых передач по отношению к фрикционным.
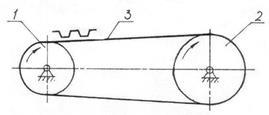 
а б
Рис. 9
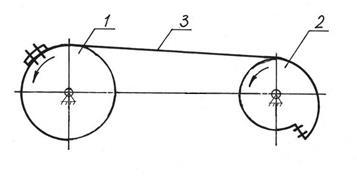
В передачах с жестким креплением разомкнутого гибкого звена к ведущему 1 и ведомому 2 звеньям (рис. 10) исключается возможность его проскальзывания, чем обеспечивается точность передачи. Недостатком таких передач является ограничение вращения ведущего и ведомого звеньев в одном направлении углом, меньшим 2π.
ЛИТЕРАТУРА
1
|
Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное пособие. М.: – Высш. шк., 2001. – 480 с. |
2001 |
| 2 |
Сурин В.М. Техническая механика: Учебное пособие. – Мн.: БГУИР, 2004. – 292 с. |
2004 |
3
|
Ванторин В.Д. Механизмы приборных и вычислительных систем: Учебное пособие. – М.: Высш. шк., 1999. – 415 с.
|
1999 |
|