Контрольная работа: Построение эпюр нормальных и касательных напряжений

Контрольная работа

Материал: сталь 40.

n = 4, a = 1,4 м

P = 1,7qa т, q = 3 т/м

М₀ = 2,3qa² т·м

Решение.

1. Построение эпюр поперечных сил и изгибающих моментов

Определим расчетную нагрузку:

Р_р = Р · n = 1,7 · 3 · 1,4 · 4 = 28,56 т

q_p = q · n = 3 · 4 = 12 т/м

М_р = М₀ · n = 2,3 · 3 · 1,4² · 4 = 54,1 т · м

Q_p = q_p · a = 12 · 1,4 = 16,8 т

Схему нагружения балки заменим ее моделью, в которой действующие на балку связи заменим силами.

Определим реакции опор. Составим следующие уравнения:

∑М_А = 0

Q_p · 0,5a + M_p – P_p · 2a + Q_p · 2,5a + P_p · 3a – R_E · 4a = 0

R_E = (Q_p · 3a + M_p + P_p · a) / 4a = (16,8 · 3 · 1,4 + 54,1 + 28,56 · 1,4) / 4 · 1,4 = 29,4 т

∑М_Е = 0

R_А · 4a - Q_p · 3,5a + M_p + P_p · 2a - Q_p · 1,5a - P_p · a = 0

R_А = (Q_p · 5a - M_p - P_p · a) / 4a = (16,8 · 5 · 1,4 - 54,1 - 28,56 · 1,4) / 4 · 1,4 = 4,2 т

Проверка:

∑F = 0

R_А - Q_p + P_p - Q_p - P_p + R_E = 0

4,2 – 16,8 + 28,56 – 16,8 – 28,56 + 29,4 = 0 – равенство верно.

Построим эпюру поперечных сил методом характерных точек, ходом слева:

F_A ^пр = R_А = 4,2 т

F_В ^лев = F_A ^пр - q_p · а = 4,2 – 12 · 1,4 = -12,6 т

F_В ^пр = F_В ^лев = -12,6 т

F_С ^лев = F_В ^пр = -12,6 т

F_С ^пр = F_С ^лев + Р_р = -12,6 + 28,56 = 15,96 т

F_D ^лев = F_С ^пр - q_p · а = 15,96 - 12 · 1,4 = -0,84 т

F_D ^пр = F_D ^лев - Р_р = -0,84 – 28,56 = -29,4 т

F_Е ^лев = F_D ^пр = -29,4 т

Строим эпюру изгибающих моментов, методом характерных точек ходом слева (рис. 1). Правую часть до рассматриваемого сечения мысленно отбрасываем. Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки.

М_А = 0

М_В ^лев = R_A · a – q_p · a · 0,5a = 4,2 · 1,4 – 12 · 1,4 · 0,5 · 1,4 = -5,88 т · м

М_В ^пр = R_A · a – q_p · a · 0,5a + М_р = 4,2 · 1,4 – 12 · 1,4 · 0,5 · 1,4 + 54,1 = 48,22 т · м

М_С = R_A · 2a – q_p · a · 1,5a + М_р = 4,2 · 2 · 1,4 – 12 · 1,4 · 1,5 · 1,4 + 54,1 = 30,58 т · м

М_D = R_A · 3a – q_p · a · 2,5a + М_р + P_p · a – q_p · a · 0,5a =

= 4,2 · 3 · 1,4 – 12 · 1,4 · 3 · 1,4 + 54,1 +28,56 · 1,4 = 41,16 т · м

М_E = 0

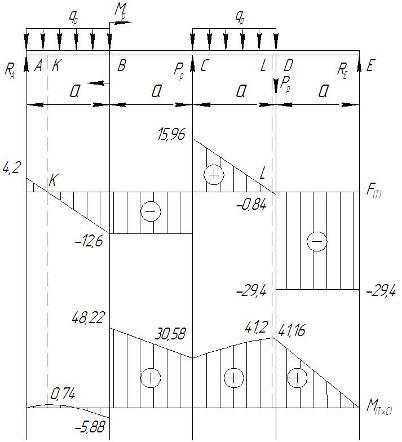
Рис. 1

Необходимо также найти моменты в сечениях К и L.

Прежде чем определить момент в сечении К, необходимо найти расстояние х = АК. Составим выражение для поперечной силы в этом сечении и приравняем его к нулю.

F_K = R_A - q_p · x = 0

x = R_A / q_p = 4,2/12 = 0,35 м

Определим момент в точке К:

М_К = R_A · x – q_p · х · 0,5х = 4,2 · 0,35 – 12 · 0,35 · 0,5 · 0,35 = 0,74 т · м

Аналогично определяем момент в точке L.

x₁ = CL

F_L = R_A – q_p · a +P_p – q_p · x₁ = 0

x₁ = (R_A – q_p · a + P_p )/ q_p = (4,2 – 12 · 1,4 + 28,56)/12 = 1,33 м

М_L = R_A (2a + x₁ ) – q_p · a (1,5a + x₁ ) + M_P + P_P · x₁ - q_p · x₁ · 0,5x₁ =

= 4,2 (2·1,4 + 1,33) – 12 · 1,4(1,5 · 1,4 + 1,33) + 54,1 + 28,56 · 1,33– 12 · 1,33 · 1,33 · 0,5 =41,2 т · м

По найденным точкам строим эпюру изгибающих моментов (рис. 1).

2. Определение необходимого осевого момента сопротивления изгибу из условия прочности

Условие прочности на изгиб:

|σ_max | = |M_max | / W_тр ≤ [σ]

Из эпюры изгибающих моментов:

M_max = 48,22 т · м = 48,22 · 10⁴ Н · м – максимальный изгибающий момент.

[σ] = 650 МПа – допускаемое нормальное напряжение для стали 40.

Требуемый осевой момент сопротивления изгибу из условия прочности:

W_тр ≥ |M_max | / [σ] = (48,22 · 10⁴ ) / 650 · 10⁶ = 0,074 · 10^-2 м³

Исследуем поперечные сечения различных форм (двутавр, швеллер, прямоугольник, квадрат, круг, треугольник)

Круг:

W_кр = πd³ / 32 = W_тр

d = = = 0,2 м

S_кр = πd² / 4 = (3,14 · 0,2² ) / 4 = 0,0314 м² = 314 см² – площадь поперечного сечения.

Квадрат:

W_к = b³ / 6 = W_тр

d = = = 0,16 м

S_к = b² = 0,16² = 0,0256 м² = 256 см² – площадь поперечного сечения.

Прямоугольник:

W_п = ba² / 6 = W_тр ; a > b; возьмем a = 2b.

W_тр = 4b³ / 6; b = = = 0,1 м; a = 2 · 0,1 = 0,2 м

S_п = аb = 0,1 · 0,2 = 0,02 м² = 200 см² – площадь поперечного сечения.

Треугольник. При вычислении напряжения в вершине треугольника.

W_т = bh² / 24 = W_тр ; b – сторона треугольника, h – высота.

Возьмем: h = b /

W_тр = b³ / 48; b = = = 0,33 м; h = 0,33 / = 0,23 м

S_тр = 0,5hb = 0,5 · 0,33 · 0,23 = 0,038 м² = 380 см² – площадь поперечного сечения.

Швеллер.

По справочникам определим швеллер.

Берем швеллер №40. W_x = 761 cм³ ; h = 0,4 м; b = 0,115 м.

S_ш = 61,5 см² – площадь поперечного сечения.

Двутавр.

По справочникам определим двутавр.

Берем двутавр №36. W_x = 743 cм³ ; h = 0,36 м; b = 0,145 м.

S_ш = 61,9 см² – площадь поперечного сечения.

3. Оценка рациональной формы поперечного сечения с точки зрения прочности

Наиболее рациональным по расходу материала является швеллер или двутавр, так как для обеспечения прочности при одинаковых условиях площадь поперечного сечения у них наименьшая. Выбираем двутавр.

4. Проверка выбранного поперечного сечения на прочность касательного напряжения

Условие прочности по касательным напряжениям имеет вид:

τ_max = ≤ [τ]

[τ] = 390 МПа – допускаемое касательное напряжение.

Из эпюры поперечных сил:

Q_max = 29,4 т = 29,4 · 10⁴ Н – максимальная поперечная сила.

Из справочника (двутавр №36):

S_x = 423 см³ = 423 · 10^-6 м³ – статический момент полусечения расположенного выше или ниже нейтральной оси.

I_x = 13380 cм⁴ = 13380 · 10^-8 м⁴ – момент инерции всего сечения относительно нейтральной линии.

b = d = 7,5 мм = 0,0075 м – толщина стенки двутавра.

τ_max = = 124 · 10⁶ Па = 124 МПа

τ_max = 124 МПа ≤ [τ] = 390 МПа

5. Построение эпюр нормальных и касательных напряжений в опасном сечении балки

Определим наибольшие нормальные напряжения в сечении балки с максимальным изгибающим моментом.

σ_max = ± M_max / W_x = ±(48,22 · 10⁴ ) / 0,000743 = ± 648 МПа,

_min

так как для двутавра №36 W_x = 743 см³ = 0,000743 м³ .

Из теории известно, что наибольшие нормальные напряжения при поперечном изгибе возникают в крайних волокнах сечения, в нейтральном слое напряжение равно нулю. Строим эпюру нормальных напряжений. Для этого в произвольном масштабе изображаем сечение двутавра. Параллельно вертикальной оси двутавра проводим нулевую линию и откладываем от нее по разные стороны на уровне крайних волокон σ_max и σ_min . Соединяем эти точки прямой линией.

Наибольшие касательные напряжения найдены выше. τ_max = 124 МПа

Наибольшие касательные напряжения по высоте сечения возникают на уровне нейтральной оси.

Строим эпюру касательных напряжений (рис. 2).

На нулевой линии на уровне нейтральной оси откладываем τ_max . Зная характер эпюры, даем ее полное изображение.

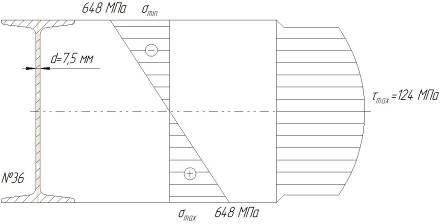
Рис. 2.

6. Проверка на прочность балки по эквивалентным напряжениям

Рассмотрим элемент, вырезанный в районе точки А (рис. 3). На гранях этого элемента, совпадающих с поперечными сечениями, возникают максимальные нормальные напряжения. В точке А возникает линейное напряженное состояние, поэтому условие прочности имеет вид:

σ_max ≤ [σ]

Очевидно, что:

σ_max = σ_А = M_max / W_x = (48,22 · 10⁴ ) / 0,000743 = 648 МПа

σ_max = 648 МПа ≤ [σ] = 650 МПа.

Рассмотрим элемент, вырезанный в районе точки В (рис. 3). На его гранях, совпадающих с поперечными сечениями, возникают максимальные касательные напряжения (точка В находится в нейтральном слое).

τ_max = τ_В = = = 124 · 10⁶ Па = 124 МПа

В точках нейтрального слоя возникает плоское напряженное состояние – чистый сдвиг. Как известно, при чистом сдвиге:

σ₁ = |σ₃ | = τ; то есть:σ₁ = |σ₃ | = τ_max = τ_В = 124 МПа

По гипотезе прочности наибольших касательных напряжений:

σ_экв = σ₁ – (-σ₃ ) = σ₁ + σ₃ = 2τ_В = 2 · 124 = 248 МПа

σ_экв = 248 МПа ≤ [σ] = 650 МПа.

Вероятно опасной точкой может быть точка С (точка на границе полки и стенки двутавра). В этой точке возникают нормальные напряжения, близкие по значению к максимальным и значительные касательные напряжения (рис. 3).

σ_С = = = 604 · 10⁶ Па = 604 МПа

τ_С = = = 91 · 10⁶ Па = 91 МПа

S_x ’ – статический момент площади полки относительно оси х. Принимая полку за прямоугольник с размерами: 145х12,3, находим:

S_x ’ = 145 · 12,3 · 173,85 = 3,1 · 10⁵ мм³ = 3,1 · 10^-4 м³

В точке С возникает плоское напряженное состояние. По гипотезе наибольших касательных напряжений находим:

σ_экв = = = 631 МПа

σ_экв = 631 МПа ≤ [σ] = 650 МПа.

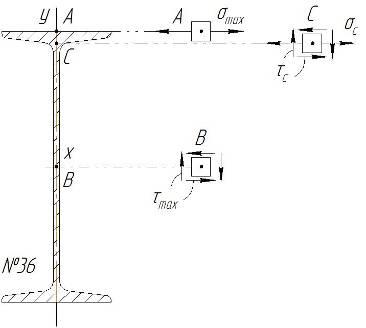
Рис. 3.