Содержание
Вступление
1. Кинетический и силовой расчёт привода
1.1 Кинематическая схема привода
1.2 Выбор двигателя
1.3 Общее передаточное число и разбиение его по степеням
1.4 Силовые и кинематические параметры привода
2. Расчет клиноременной передачи
2.1 Исходные данные для расчёта передачи
2.2 Механический расчет
3. Расчет цилиндрической 3.1. Кинематическая схема передачи и исходные данные для расчета
3.2 Выбор материала и определение допустимых напряжений
3.3 Определение геометрических параметров
3.4 Проверочный расчет передачи
3.5 Определение сил в зацеплении (см. рис. 3.3)
4. Расчёт цилиндрической косозубой передачи || ступени
4.1 Кинематическая схема передачи и исходные данные для расчета
4.2 Выбор материала и определение допустимых напряжений
4.3 Определение геометрических параметров
4.4 Проверочный расчет передачи
4.5 Определение сил в зацеплении (см. рис. 3.3)
5. Условный расчет валов
5.1 Определение диаметров входного валаредуктора
6. Определение конструктивных размеров зубчатых колес
6.1 Размеры зубчатых колес цилиндрической передачи I ступени
6.2 Размеры зубчатых колес цилиндрической передачи II ступени
6.3 Определяем размеры цилиндрического колеса (рис.6.1.)
6.4 Определение диаметров выходного вала
7. Конструктивные размеры корпуса и крышки редуктора
7.1 Определение конструктивных размеров корпуса и крышки редуктора, согласно табл. 4.2, 4.3, [1]
7.2 Размеры необходимые для черчения
8. Выбор шпонок и их проверочный расчет
9. Расчёт промежуточного вала редуктора на статическую способность и долговечность
9.1 Расчет вала на несущую способность
9.2 Расчет вала на прочность
10. Расчет подшипников качения
10.1 Определение реакции в опорах
10.2 Определение коэффициентов
10.3 Определение эквивалентной нагрузки
10.4 Определяем долговечность подшипников
10.5 Выбор муфты
10.6 Проверочный расчёт зубчатой муфты
11. Выбор и проверочный расчёт опор скольжения
Литература
Вступление
Развитие народного хозяйства Украины тесно связано с развитием машиностроения, так как материальная мощность современной страны базируется на технике – машинах, механизмах, аппаратах, приводах, которые выполняют разную полезную работу. В наше время нет ни одной области народного хозяйства, где бы не применялись машины и механизмы в широких масштабах. Благодаря этому осуществляется комплексная механизация в промышленности, в сельском хозяйстве, в строительстве, на транспорте. Это заставляет уделять большое внимание при проектировании и усовершенствования конструкций современных машин и механизмов. Машины и механизмы, которые проектируются, должны иметь высокие эксплуатационные показатели, не большое количество энергии и эксплуатационных материалов, должны быть экономичными, как в процессе производства, так и в процессе эксплуатации, удобными и безопасными в обслуживании.
1. Кинетический и силовой расчёт привода
Согласно техническому заданию на курсовой проект по дисциплине «Детали машин» необходимо спроектировать привод цепного конвейера, который состоит из двигателя, клиноременной передачи, двухступенчатого цилиндрического ора и муфты. При проектировании деталей привода использованы современные критерии оценки их работоспособности – прочность, жесткость и износостойкость. Кинематический и силовой расчеты привода
1.1 Кинематическая схема привода
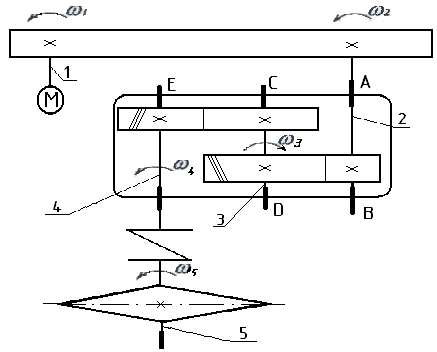
Рис 1.1
Таблица 1.1
Исходные данные для кинематического и силового расчета привода
| Название параметров |
Обозначения в формулах |
Единица измерения |
Величина параметра |
| Окружная сила |
F1 |
Н |
28000 |
| Скорость |
 |
м/с |
0,5 |
| Число зубьев |
z |
- |
9 |
| Шаг цепи |
р |
мм |
160 |
| Режим работы |
P |
- |
С |
| Число смен |
T |
- |
1 |
1.2 Выбор двигателя
Работа над курсовым проектом по дисциплине «Детали машин» подготавливает студентов к решению более сложных задач общетехнического характера в своей дальнейшей практической деятельности.
Определяем необходимое усилие на валу 1 двигателя, кВт,
 кВт кВт
где
N
5
– усилие на приводном валу 5, кВт
, ηобщ
- общий кпд.
 кВт, кВт,
ηобщ
= η12
η23
η34
η45
= 0,95· 0,95· 0,96· 0,98 = 0,85,
гдеη12=
ηкр
=
0,95 – кпд между 1 и 2 валами; η23
= ηцп
· η кр
=
0,96·0,99=0,95 – кпд между 2 и 3 валами; η34
=ηцп·
ηоп
=
0,97·0,99=0,96 – кпд между 3 и 4 валами; η45
= ηм·
ηоп
ηоп
=1·0,99·0,99=0,98 – кпд между 4 и 5 валами.
Средние значения кпд принимаем из [1], табл. 1.1
ηкр
=
0,95-кпд клиноременной передачи;
ηцп
=0,97-кпд цилиндрической передачи;
ηоп
=0,99-кпд в опорах;
ηм
=1,0-кпд муфты.
Принято, что валы привода установлены на подшипниках качения.
Определяем угловую скорость и частоту вращения вала электродвигателя.
 рад/с рад/с
где  рад/с – угловая скорость на 5 валу рад/с – угловая скорость на 5 валу
где 
 - общее передаточное отношение привода. - общее передаточное отношение привода.
 , ,
Средние значения ориентировочных передаточных чисел принимаем из [2], табл. 5.5, с 74.
  - ориентировочное передаточное число клиноременной передачи; - ориентировочное передаточное число клиноременной передачи;  - ориентировочное передаточное число цилиндрической передачи I ступени; - ориентировочное передаточное число цилиндрической передачи I ступени;  - ориентировочное передаточное число цилиндрической передачи II ступени; - ориентировочное передаточное число цилиндрической передачи II ступени;  - ориентировочное передаточное число муфты. - ориентировочное передаточное число муфты.
Определяем частоту вращения вала 1
 об/мин. об/мин.
Выбираем электродвигатель исходя из условий   . .
Из [3], табл.2.4, с.23, выбираем электродвигатель 4АН180М6,
 кВт кВт
 об/мин и для дальнейших расчётов выполняем переход от об/мин и для дальнейших расчётов выполняем переход от  к к 
 рад/с рад/с
1.3 Общее передаточное число и разбиение его по степеням
Определяем действительное общее передаточное число привода при выбранном двигателе.

Проводим разбиение  по степеням. по степеням.
Принимаем  ; ;  ; ;  . .
Тогда 
1.4 Силовые и кинематические параметры привода
Определяем мощности на валах:
 кВт
; кВт
;  кВт
; кВт
;
 кВт ; кВт ;  кВт; кВт;
 кВт
(див.розд.1.2.1.) кВт
(див.розд.1.2.1.)
Определяем угловые скорости валов:
 рад/с; рад/с;
 рад/с; рад/с;
 рад/с; рад/с;
 рад/с; рад/с;
 рад/с. рад/с.
Определяем крутящие моменты на валах:
 Нм
; Нм
;  Нм; Нм;
 Нм; Нм;
 Нм
; Нм
;
 Нм
. Нм
.
Результаты расчётов сводятся в табл.1.2 и являются исходными данными для всех следующих расчётов.
Таблица 1.2
Результаты кинетического и силового расчётов привода
Параметры
№ вала
|
N, кВт |
ω рад/с |
М,Нм
|
 |
 |
| 1 |
16,5 |
102,05 |
161,7 |
2,98 |
47,68 |
| 2 |
15,7 |
34,24 |
458,5 |
| 4 |
| 3 |
14,9 |
8,56 |
1740 |
| 4 |
| 4 |
14,3 |
2,14 |
6682 |
| 1 |
| 5 |
13 |
2,4 |
6542 |
2. Расчет клиноременной передачи
Схема клиноременной передачи

Рис 2.1
2.1 Исходные данные для расчёта передачи
Таблица 2.1
Исходные данные для расчета передачи
Параметры
№шва
|
N, кВт |
w, рад/с |
М, Нм |
ид12 |
и добщ |
| 1 |
16,5 |
102,05 |
161,7 |
2,98 |
47,68 |
| 2 |
15,7 |
34,24 |
458,5 |
2.2 Механический расчет
Сечение ремня по табл. 5.6 ([8], с. 69)
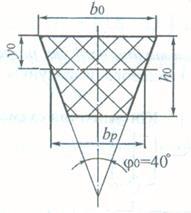
Рис 2.2
При заданном значении М принимаем сечение ремня (В).
Диаметр меньшего шкива
Минимально допустимый диаметр шкива dmin
= 63 мм
.
Для повышения коэффициента полезного действия передачи, увеличения долговечности и тяговой способности ремней, уменьшение числа ремней принимаем d
1
=100 мм.
Диаметр большего шкива: d
2
=
d
1
·i
кл
=100∙2,98=298
Скорость ремня:  ; ;
где v
– скорость ремня,  м/с. м/с.
Частота вращения ведомого вала  ; ;
где n
2
– частота вращения ведомого вала, об/мин
.; - коэффициент скольжения; принимаем - коэффициент скольжения; принимаем  = 0,01 = 0,01
 об/мин
. об/мин
.
Ориентировочное межосевое расстояние
Принимаем a
0
=400 мм.
Длина ремня
 ; ;
где L
- длина ремня, мм;
 ; ;
 ; ;
 мм. мм.
В соответствии с ГОСТ 1284.1-80 принимаем L
= 1600 мм.
Окончательное межосевое расстояние
 ; ;
 мм. мм.
Принимаем a
= 500 мм.
Наименьшее расстояние, необходимое для надевания ремня
a
наим
= a
- 0,01L
;
a
наим
= 500-0,01·1600 = 484 мм.
Наибольшее расстояние, необходимое для компенсации вытяжки ремня
a
наиб
= a
- 0,025L
;
a
наиб
= 500-0,025·1600 = 460 мм.
Коэффициент динамичности и режима работы
с
р
= 1,1
Угол обхвата
 ; ;
где  - угол обхвата, º; - угол обхвата, º;

По табл. 5.7 ( 5, с.71) величина окружного усилия р0
, передаваемого одним ремнем р0
=124 Н (на один ремень)
Допускаемое окружное усилие на один ремень
[р]=р0
×Сα
×СL
×CР
,
где Сα
=1-0,003(180-α1
)=1- 0,003(180-156,24)=0,93
Коэффициент, учитывающий длину ремня
 , так как расчетная длина L=1600=L0 , так как расчетная длина L=1600=L0
Коэффициент режима работы Ср
=1, следовательно
[р]=824∙0,93=757
где р0
=814 ( по табл. 5,7 [8], с. 71 )
Окружное усилие
 Н Н
Расчетное число ремней  ; ;  . .
Принимаем Z
= 4
3. Расчет цилиндрической 3.1. Кинематическая схема передачи и исходные данные для расчета
Кинематическая схема передачи

Рис.3.1.
Исходные данные для расчета передачи Таблица 3.1.
параметры
№ вала
|
N, кВт |
ω, рад/с |
M,Нм |
ид34 |
идобщ |
| 2 |
15,7 |
34,24 |
458,5 |
4,0 |
47,68 |
| 3 |
14,9 |
8,56 |
1740 |
3.2 Выбор материала и определение допустимых напряжений
Материалы зубчатых колес
Для уравновешивания долговечности шестерни и колеса, уменьшения вероятности заедания и лучшей приработки твердость зубьев шестерни необходимо выбирать большей, чем твердость колеса: НВш
= НВк
+
(20…50).
Так как к габаритам передачи не накладываются жесткие условия, то для изготовления зубчатых колес, из [6], принимаем материалы для шестерни – сталь 50
, для колеса – сталь 40.
Параметры материалов зубчатых колес сводим в таблицу 3.2.
Таблица 3.2
Материалы зубчатых колес.
| Материал |
Термообработка |
Предел теку-чести, σт, МПа |
Твердость, НВ |
| Шестерня |
Сталь 50 |
нормализация |
380 |
180 |
| Колесо |
Сталь 40 |
нормализация |
340 |
154 |
Допустимые контактные напряжения:
 , ,
где σН
lim
– граница контактной долговечности поверхности зубцов, соответствует базовому числу циклов изменения напряжений NН0
= 30 НВ2,4
, (при твердости поверхности зубьев ≤350 НВ,
σН
lim
b
= 2 НВ
+70):
σН
l
im
b
ш
= 2·180+70=430МПа, σН
lim
b
к
=2· 154 + 70=378 МПа;
NН0ш
= 30·1802,4
= 7,76·106
, NН0к
= 30 · 1542,4
= 5,3·106
;
S
Н
– коэффициент безопасности (запас прочности), учитывается от термообработки и характера нагрузок, принимаем S
Н
= 1,1, [6];
КН
L
– Коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется из соотношения NН0
и дополнения (NΣ
·КНЕ
); КНЕ
– коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем КНЕ
= 0,06.
NΣ
- суммарное число циклов нагрузки зубьев за все время службы передачи:
 , ,
где Lh
–время службы передачи, для односменной работы Lh
=1·104
час.
 , ,  . .
NΣш
· КНЕ
=1,96 · 108
· 0,06 = 1,17 · 106
< NН0ш
= 7,76 · 106
,
NΣк
· КНЕ
= 0,49 · 108
· 0,06 =2,9 · 106
< NН0ш
=
5,3 ·106
.
Так как в обоих случаях NН0
>NΣ
· КНЕ
, то коэффициент долговечности
 , ,
 . .
 Мпа
; Мпа
;  МПа МПа
Допустимые напряжения на изгиб.
 , ,
где σF
limb
– граница выносливости поверхности зубцов при изгибе, соответствует базовому числу циклов смены напряжений NFо
= 4 · 106
, [6], (при твердости поверхности зубьев ≤350 НВ,
σF
limb
= НВ
+ 260):
σF
limb
ш
= 180 +260 = 440МПа,
σF
limb
к
= 154 + 260 = 414 МПа;
SF
–
коэффициент безопасности (запас прочности), из [2], принимаемSF
= 1,8, KFL
– коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется соотношением NF0
и (NΣ
KF
Е
); KF
Е
– коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем KF
Е
= 0,02.
NΣ
m
·KF
Е
= 1,05·108
·0,02 = 2,1·106
< NF0
= 4·106
,
NΣк
·KF
Е
= 0,26·108
·0,02 = 0,52·106
< NF0
= 4·106
.
Так как в обоих случаях NF0
> NΣ
KF
Е
, то согласно [ ], коэффициент долговечности:
 ; ;  . .
KFC
- коэффициент реверсивности нагрузки, для нереверсивной передачиКН
L
– 1,0, [6].
 ; ; 
Допустимые максимальные контактные напряжения.
[σН
]max
= 2,8 σТ
.
[σН
]max
ш
= 2,8·380 = 1064 МПа
, [σН
]max
к
=2,8·340=952 МПа.
Допустимые максимальные напряжения на изгиб.
[σF
]max
= 0,8 σТ
.
[σF
]max
ш
= 0,8·380 = 304 МПа.,
[σF
]max
к
=
0,8·340 = 272 МПа
.
3.3 Определение геометрических параметров
Межосевое расстояние.
Из условий контактной усталости поверхности зубьев:
 , ,
где Ка
– коэффициент межосевого расстояния, из [6], для косозубых передач Ка
= 4300 Па1/3
;  - коэффициент ширины зубчатого венца по межосевому расстоянию, из [6], для косозубой передачи принимаем - коэффициент ширины зубчатого венца по межосевому расстоянию, из [6], для косозубой передачи принимаем
ψ
ba
= 0,45; и
= ид
34
= 4;
КНβ
– коэффициент распределения нагрузки по ширине венца зубчатого колеса, из [6], табл.1.2, в зависимости от ψ
bd
= 0,5 ψ
ba
(и+
1) = 0,5 · 0,45 · (4+1) = 1,13, для косозубой передачи КНβ
= 1,046;[σН
] – наименьшее из двух значений (шестерни и колеса) допустимых контактных напряжений, МПа
.
 , ,

Определение модуля.
Первоначальное значение расчетного модуля зубьев определяется

где β
– угол наклона зубьев, для косозубой передачи β
= 20°;
Zш
– число зубьев шестерни, согласно [6] принимаем Zш
= 20;
Zш
– число зубьев колеса, Zк
= Zш
и
= 20·4 = 80.
Согласно [6], табл.1.3, принимаем m
п
=
5 мм.
- ширина: b
к
= ψ
d
а
аw
= 0,45 · 266 = 119,7 мм.
Принимаем b
к
= 120 мм.
3.4 Проверочный расчет передачи
Расчет на контактную усталость.

где ZН
– коэффициент, учитывающий форму спряженных поверхностей зубьев: для косозубых - ZН
= 1,75, [6];
ZМ
= 275 · 103
Па1/2
- коэффициент учитывающий механические свойства материалов зубчатых колес, [6];
ZЕ
- коэффициент суммарной длинны контактный линий спряженных зубьев: для косозубых - ZЕ
= 0,8, [6];
КН
= КНа
КН β
КН
V
– коэффициент нагрузки : КНа
– коэффициент распределения нагрузки между зубьями из [6], табл. 1.4, КН а
= 1,15; КН β
= 1,046, см. разд.3.3.1, КН
V
– коэффициент динамической нагрузки, из [6], табл. 1.4, при
 ; К
HV
=1.02; КН
=1,15∙1,046∙1,02=1,22. ; К
HV
=1.02; КН
=1,15∙1,046∙1,02=1,22.

Так как σН
= 363 находится в пределах (0,9…1,0)[σН
], то расчет можем считать завершенным:  . .
Расчет на контактную прочность.
 , ,
где Кп
=2,2, [σН
]max
– наименьшее из двух значений (шестерни и колеса) допустимых максимальных контактных напряжений, МПа

Условие выполняется.
расчет на усталость при изгибе.
Определяем отдельно для шестерни и колеса по формуле
 , ,
где - Y
F
- коэффициент формы зуба, из [6], табл. 1.7, по эквивалентному числу зубьев Z
V
,
для косозубой передачи:  , YFш
=3,92; , YFш
=3,92;  ,YFк
= 3,6. ,YFк
= 3,6.
Y
E
- коэффициент перекрытия зубьев, согласно [6] принимаем Y
E
=1,0.
Yβ
- коэффициент наклона зубьев, согласно [6] для косозубых передач принимается:
КF
= КFа
К Fβ
КF
V
- коэффициент нагрузки: КFа
– коэффициент распределения нагрузки между зубьями для косозубых - КFа
=1,0, [6], табл. 1,8; К Fβ
–коэффициент
Геометрические размеры цилиндрической зубчатой передачи

Рис 3.2.
Геометрический расчет передачи (см. рис. 3.2).
Межосевое расстояние

Принимаем аw
= 266 мм.
Уточняем угол наклона зубьев

Размеры шестерни:
- делительный диаметр: 
- диаметр вершин зубьев: d
аш
= d
ш
+ 2mn
= 106,4+ 2 · 5= 116,4мм;
- диаметр впадин: d
ƒш
= d
ш
– 2,5mn
= 106,4 – 2,5 · 5= 93,9мм;
- ширина: b
ш
=b
к
+ 5 мм
= 120 + 5 = 125 мм.
Размеры колеса:
-делительный диаметр 
- диаметр вершин зубьев:d
ак
= d
к
+ 2mn
= 425,5 +2 · 5 = 696 мм
;
- диаметр впадин: d
ƒк
= d
к
– 2,5mn
= 425,5 – 2,5 · 5 = 413 мм;
распределения нагрузки по ширине венца зубчатого колеса, из [6], табл. 1.9, в зависимости от ψ
ba
= 1, 13 (см. разд. 3.3.1.) для косозубой передачи К Fβ
= 1,09; КF
V
- коэффициент динамической нагрузки, выбирается из табл. 1.10, [6], при КF
V
= 1,05; КF
= 1,00 · 1,09 · 1,05 = 1,14.


Условия выполняются.
Расчет на прочность при изгибе.
Выполняется отдельно для шестерни и колеса при действии кратковременных максимальных нагрузок (в период пуска двигателя).
σF
ma
х
= σF
Кп
≤ [σF
]max΄
где Кп
– коэффициент перегрузки, из [2], табл. 1, с. 249 - Кп
=2,2.
σF
ma
х ш
= 114 · 2,2 = 250,8 МПа
≤ [σF
]max
ш
= 304 МПа,
σF
ma
х к
= 92 · 2,2 = 202,4 МПа
≤ [σF
]max
к
= 272 МПа.
Условия выполняются.
3.5 Определение сил в зацеплении (см. рис. 3.3)
- окружная сила 
- радиальная сила 
- осевая сила Fаш
= Fак
= F
t
к
tgβ
= 8651· tg
19,95
0
= 3139 Н
Схема сил в зацеплении
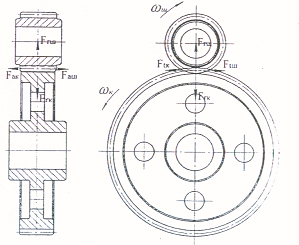
Рис.3.3.
4. Расчёт цилиндрической косозубой передачи || ступени
4.1 Кинематическая схема передачи и исходные данные для расчета
Кинематическая схема передачи
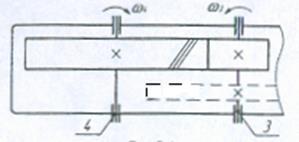
Рис.4.1.
Исходные данные.
Таблица 4.1.
Исходные данные для расчета передачи
параметры
№ вала
|
N, кВт |
ω, рад/с |
M,Нм |
ид34 |
идобщ |
| 3 |
14,9 |
8,56 |
1740 |
4 |
47,68 |
| 4 |
14,3 |
2,14 |
6682 |
4.2 Выбор материала и определение допустимых напряжений
Материалы зубчатых колес.
Для уравновешивания долговечности шестерни и колеса, уменьшения вероятности заедания и лучшей приработки твердость зубьев шестерни необходимо выбирать большей, чем твердость колеса: НВш
= НВк
+
(20…50).
Так как к габаритам передачи не накладываются жесткие условия, то для изготовления зубчатых колес, из [6], принимаем материалы для шестерни – сталь 50
, для колеса – сталь 40.
Параметры материалов зубчатых колес сводим в таблицу 3.2.
Таблица 4.2.
Материалы зубчатых колес
| Материал |
Термообработка |
Предел теку-чести, σт, МПа |
Твердость, НВ |
| Шестерня |
Сталь 50 |
нормализация |
380 |
180 |
| Колесо |
Сталь 40 |
нормализация |
340 |
154 |
Допустимые контактные напряжения:
 , ,
где σН
lim
– граница контактной долговечности поверхности зубцов, соответствует базовому числу циклов изменения напряжений NН0
= 30 НВ
2,4
, (при твердости поверхности зубьев ≤350 НВ,
σН
lim
b
= 2 НВ
+70):
σН
l
im
b
ш
= 2·180+70=430МПа, σН
lim
b
к
=2· 154 + 70=378 МПа;
NН0ш
= 30·1802,4
= 7,76·106
, NН0к
= 30 · 1542,4
= 5,3·106
;
KFL
– коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется соотношением NF0
и (NΣ
KF
Е
); KF
Е
– коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем KF
Е
= 0,02.
NΣ
m
·KF
Е
= 1,05·108
·0,02 = 2,1·106
< NF0
= 4·106
,
NΣк
·KF
Е
= 0,26·108
·0,02 = 0,52·106
< NF0
= 4·106
.
Так как в обоих случаях NF0
> NΣ
KF
Е
, то согласно [ ], коэффициент долговечности:
 ; ;
 . .
KFC
- коэффициент реверсивности нагрузки, для нереверсивной передачи КН
L
– 1,0, [6].
 ; ; 
Допустимые максимальные контактные напряжения.
[σН
]max
= 2,8 σТ
.
[σН
]max
ш
= 2,8·380 = 1064 МПа
, [σН
]max
к
=2,8·340=952 МПа.
Допустимые максимальные напряжения на изгиб.
[σF
]max
= 0,8 σТ
.
[σF
]max
ш
= 0,8·380 = 304 МПа.,
[σF
]max
к
=
0,8·340 = 272 МПа
.
4.3 Определение геометрических параметров
Межосевое расстояние.
Из условий контактной усталости поверхности зубьев:
 , ,
где Ка
– коэффициент межосевого расстояния, из [6], для косозубых передач Ка
= 4300 Па1/3
;  - коэффициент ширины зубчатого венца по межосевому расстоянию, из [6], для косозубой передачи принимаем - коэффициент ширины зубчатого венца по межосевому расстоянию, из [6], для косозубой передачи принимаем
ψ
ba
= 0,45; и
= ид
34
= 4;
КНβ
– коэффициент распределения нагрузки по ширине венца зубчатого колеса, из [6], табл.1.2, в зависимости от ψ
bd
= 0,5 ψ
ba
(и+
1) = 0,5 · 0,45 · (4+1) = 1,13, для косозубой передачи КНβ
= 1,046;[σН
] – наименьшее из двух значений (шестерни и колеса) допустимых контактных напряжений, МПа
.
 , ,

Определение модуля.
Первоначальное значение расчетного модуля зубьев определяется

S
Н
– коэффициент безопасности (запас прочности ), зависит от термообработки и характера нагрузок, принимаем S
Н
= 1,1, [6];
КН
L
– Коэффициент долговечности, который учитывает время службы и режим нагрузок передачи, определяется из соотношения NН0
и дополнения (NΣ
·КНЕ
); КНЕ
– коэффициент интенсивности режима нагрузки, из [6], табл. 1.1, для легкого режима принимаем КНЕ
= 0,06.
NΣ
- суммарное число циклов нагрузки зубьев за все время службы передачи:
 , ,
где Lh
–время службы передачи, для односменной работы Lh
=1·10 4
час.
 , ,  . .
NΣш
· КНЕ
=0,49 · 108
· 0,06 = 2,94 · 106
< NН0ш
= 7,76 · 106
,
NΣк
· КНЕ
= 0,12 · 108
· 0,06 = 0,72 · 106
< NН0ш
=
5,3 ·106
.
Так как в обоих случаях NН0
>NΣ
· КНЕ
, то коэффициент долговечности
 , ,
 . .
 Мпа
; Мпа
;  МПа МПа
Допустимые напряжения на изгиб.
 , ,
где σF
limb
– граница выносливости поверхности зубцов при изгибе, соответствует базовому числу циклов смены напряжений NFо
= 4 · 106
, [6], (при твердости поверхности зубьев ≤350 НВ,
σF
limb
= НВ
+ 260):
σF
limb
ш
= 180 +260 = 440МПа,
σF
limb
к
= 154 + 260 = 414 МПа;
SF
–
коэффициент безопасности (запас прочности), из [2], принимаемSF
= 1,8,
где β
– угол наклона зубьев, для косозубой передачи β
= 20°;
Zш
– число зубьев шестерни, согласно [6] принимаем Zш
= 20;
Zш
– число зубьев колеса, Zк
= Zш
и
= 20·4 = 80.
Согласно [6], табл.1.3, принимаем m
п
=
8,0 мм
.
- ширина: b
к
= ψ
d
а
аw
= 0,45 · 425 = 191,25 мм
.
Принимаем b
к
= 220 мм
.
4.4 Проверочный расчет передачи
Расчет на контактную усталость. распределения нагрузки по ширине венца зубчатого колеса, из [6], табл. 1.9, в зависимости от ψ
ba
= 1, 13 (см. разд. 3.3.1.) для косозубой передачи К Fβ
= 1,09; КF
V
- коэффициент динамической нагрузки, выбирается из табл. 1.10, [6], при ν = 1,77 м/с, КF
V
= 1,05; КF
= 1,00 · 1,09 · 1,05 = 1,14.


Условия выполняются.
Расчет на прочность при изгибе.
Выполняется отдельно для шестерни и колеса при действии кратковременных максимальных нагрузок (в период пуска двигателя).
σF
ma
х
= σF
Кп
≤ [σF
]max΄
где Кп
– коэффициент перегрузки, из [2], табл. 1, с. 249 - Кп
=2,0.
σF
ma
х ш
= 103 · 2,2 = 226,6 МПа
≤ [σF
]max
ш
= 304 МПа,
σF
ma
х к
= 84 · 2,2 = 184,8 МПа
≤ [σF
]max
к
= 272 МПа.
Условия выполняются.
4.5 Определение сил в зацеплении (см. рис. 3.3)
- окружная сила 
- радиальная сила 
- осевая сила Fаш
= Fак
= F
t
к
tgβ
= 20470 · tg
20° = 7450 Н
Схема сил в зацеплении

Рис.4.3.

где ZН
– коэффициент, учитывающий форму спряженных поверхностей зубьев: для косозубых - ZН
= 1,75, [6];
ZМ
= 275 · 103
Па1/2
- коэффициент учитывающий механические свойства материалов зубчатых колес, [6];
ZЕ
- коэффициент суммарной длинны контактный линий спряженных зубьев: для косозубых - ZЕ
= 0,8, [6];
КН
= КНа
КН β
КН
V
– коэффициент нагрузки : КНа
– коэффициент распределения нагрузки между зубьями из [6], табл. 1.4, КН а
= 1,15; КН β
= 1,046, см. разд.3.3.1, КН
V
– коэффициент динамической нагрузки, из [6], табл. 1.4, при
 ; К
HV
=1.02; КН
=1,15∙1,046∙1,02=1,22. ; К
HV
=1.02; КН
=1,15∙1,046∙1,02=1,22.

Так как σН
= 363 находится в пределах (0,9…1,0)[σН
], то расчет можем считать завершенным:  . .
Расчет на контактную прочность.
 , ,
где Кп
=2,2, [σН
]max
– наименьшее из двух значений (шестерни и колеса) допустимых максимальных контактных напряжений, МПа

Условие выполняется.
расчет на усталость при изгибе.
Определяем отдельно для шестерни и колеса по формуле
 , ,
где - Y
F
- коэффициент формы зуба, из [6], табл. 1.7, по эквивалентному числу зубьев Z
V
,
для косозубой передачи:  , YFш
=3,92; , YFш
=3,92;  ,YFк
= 3,6. ,YFк
= 3,6.
Y
E
- коэффициент перекрытия зубьев, согласно [6] принимаем Y
E
=1,0.
Yβ
- коэффициент наклона зубьев, согласно [6] для косозубых передач принимается:
КF
= КFа
К Fβ
КF
V
- коэффициент нагрузки: КFа
– коэффициент распределения нагрузки между зубьями для косозубых - КFа
=1,0, [6], табл. 1,8; К Fβ
–коэффициент
Геометрические размеры цилиндрической зубчатой передачи

Рис 4.2.
Геометрический расчет передачи (см. рис. 4.2).
Межосевое расстояние

Принимаем аw
= 425 мм
.
Уточняем угол наклона зубьев

Размеры шестерни:
- делительный диаметр: 
- диаметр вершин зубьев: d
аш
= d
ш
+ 2mn
= 170 + 2 · 8,0 = 186мм;
- диаметр впадин: d
ƒш
= d
ш
– 2,5mn
= 170 – 2,5 · 8,0 = 150 мм
;
- ширина: b
ш
b
к
+ 5 мм
= 220 + 5 = 225 мм
.
Размеры колеса:
-делительный диаметр 
- диаметр вершин зубьев:d
ак
= d
к
+ 2mn
= 680 +2 · 8,0 = 696 мм
;
- диаметр впадин: d
ƒк
= d
к
– 2,5mn
= 680 – 2,5 · 8,0 = 660 мм;
5. Условный расчет валов
При отсутствии данных о моменте изгиба, диаметр вала определяют приблизительно по известному крутящему моменту из условий прочности на кручение по заниженным значениям допустимых напряжений:

где i-
номер вала, j
- номер участка ступенчатого вала, Мi
- крутящий момент на i-
тому валу, принимаем из табл.
1.2. Согласно рекомендаций [4], с.53, принимаем пониженные допускаемые напряжения кручения, для валов редукторов общего назначения, [τк
] = 25 МПа.
5.1 Определение диаметров входного валаредуктора
Схема входного вала редуктора

Рис. 5.1.

Согласно [7], с. 6 полученный диаметр округляем до ближнего большего значения из стандартного ряда Ra
40 ГОСТ6636-69.
Принимаем d
21
= 50 мм.
Диаметры других участков вала выбираем из стандартного ряда Ra
40 ГОСТ6636-69.
Принимаем d
22
=60 мм
d
23
= 60 мм
d
24
= 65 мм.
.2. Определение диаметров промежуточного вала редуктора
Схема промежуточного вала редуктора

Рис. 5.1.

6. Определение конструктивных размеров зубчатых колес
6.1 Размеры зубчатых колес цилиндрической передачи
I
ступени
Устанавливаем способ изготовления шестерни и вала – вместе или отдельно. Согласно рекомендаций [1], если  - отдельно, - отдельно,  – вместе, где d
fш
- диаметр впадин шестерни (d
fш
= 200,7 мм
, см. разд.3.3.3.11),
d
вш
- диаметр участка вала под шестерню (d
вш
= 60 мм
,
см. разд. 5.2) – вместе, где d
fш
- диаметр впадин шестерни (d
fш
= 200,7 мм
, см. разд.3.3.3.11),
d
вш
- диаметр участка вала под шестерню (d
вш
= 60 мм
,
см. разд. 5.2)
 -выполняем вместе. -выполняем вместе.
6.2 Размеры зубчатых колес цилиндрической передачи
II
ступени
Устанавливаем способ изготовления шестерни и вала – вместе или отдельно. Согласно рекомендаций [1], если  - отдельно, - отдельно,  – вместе где d
fш
– диаметр впадин шестерни,,d
fш
=150 мм,
d
вш
- диаметр участка вала под шестерню d
вш
=
d
24
=75 мм. – вместе где d
fш
– диаметр впадин шестерни,,d
fш
=150 мм,
d
вш
- диаметр участка вала под шестерню d
вш
=
d
24
=75 мм.
 -
выполняется отдельно. -
выполняется отдельно.
6.3 Определяем размеры цилиндрического колеса (рис.6.1.)
Схема колеса зубчатого

Рис.6.1.
Согласно [7], с.6 полученный диаметр округляем до ближайшего большего значения из стандартного ряда Ra
40 ГОСТ6636-69.
Принимаем d
31
= 70 мм
.
Диаметры других участков вала выбираем из стандартного ряда Ra
40 ГОСТ6636-69.
Принимаем d
32
= 75 мм
;
d
33
= 80 мм
.
6.4 Определение диаметров выходного вала
Схема выходного вала редуктора

Рис. 5.2.

Согласно [7], с.6 полученный диаметр округляем до ближайшего большего значения из стандартного ряда Ra
40 ГОСТ6636-69.
Принимаем d
41
= 110 мм
.
Диаметры других участков вала выбираем из стандартного ряда Ra
40 ГОСТ6636-69.
Принимаем d
42
= 115 мм
;d
43
= 120 мм
;d
44
= 130 мм
.
d
45
= 140 мм.
Общая ширина зубчатого венца в=
220 мм.
Диаметр ступицы d
с
= 1,6d
в
= 1,6 · 130 = 208 мм
Длина ступицы lс
= (1,2…1,5)d
в
= 1,5 · 130 = 195 мм
.
Принимаем 220 мм
Толщина обода δ0
= (2,5…4)mn
4 · 8 = 32 мм
Толщина диска с
= (0,2…0,4)b
= 0,4·220 = 88 мм
Принимаем 90 мм
.
Диаметр отверстий в диске d
отв
= 0,25[d
об
–(d
в
+ 2 δст
)],
где , d
об
= df
ш
- 2 δ0
= 660 – 2 · 39 = 582 мм
.
, d
об
= df
ш
- 2 δ0
= 660 – 2 · 39 = 582 мм
.
d
отв
= 0,25[582–(130+ 2 ·
39)] = 93,5 мм
,
принимаем d
отв
= 95 мм
.
Диаметр центров отверстий в диске
d
0
= 0,5(d
в
2 δс
+d
об
) = 0,5 · (130 +2 · 38 + 582) = 395 мм
.
7. Конструктивные размеры корпуса и крышки редуктора
7.1 Определение конструктивных размеров корпуса и крышки редуктора, согласно табл. 4.2, 4.3, [1]
Толщина стенки корпуса редуктора:
δ
= 0,025aw
+ 3 = 0,025 · 425 + 3 = 13,6 ≈ 14 мм
,
где aw
– межосевое расстояние зубчатых передач редуктора.
Толщина стенки крышки редуктора:
δ1
= 0,02аw
+ 3 = 0,02 · 425 + 3 = 11,5 ≈ 12 мм
.
Толщина верхнего фланца корпуса:
S
= (1,5…1,75) · δ
=(1,5…1,75) ∙14 = 21…24,5 = 24 мм
.
Толщина нижнего фланца корпуса:
S
2
= 2,35 δ
= 2,35 ∙14 = 32,9 ≈ 33мм.
Толщина фланца крышки редуктора:
S
1
= (1,5…1,75) · δ1
=(1,5…1,75) ·12 = 18…21 = 20 мм
.
Диаметр фундаментных болтов:
d
1
= 0,072aw
+ 12 = 0,072 · 425 + 12 = 37,9 ≈ 39 мм
,
Диаметр болтов, стягивающих корпус и крышку возле бобышек:
d
2
= (0,7…0,75) ·d
1
=(0,7…0,75) ∙39 = 27,3…29,25 = 27 мм
.
Диаметр болтов, стягивающих фланцы корпуса и крышки редуктора:
d
3
= (0,5…0,6) ·d
1
=(0,5…0,6) ∙24 = 12…14,4 = 14мм.
Ширина опорной поверхности нижнего фланца корпуса:
m
= k + 1,5 δ
= 60 + 1,5 ∙ 14 = 81мм.
Толщина ребер корпуса:
с1
= (0,8…1) · δ
= (0,8…1) ·∙14 = 10,4…14 = 12мм.
7.2 Размеры необходимые для черчения
Минимальный зазор между колесом и корпусом:
b
= 1,2 δ
= 1,2 · 14 = 16,8 мм
.
Расстояние от внутренней стенки до торца вращающейся детали:
е1
= (1,0…1,2) ∙
δ
= (1,0…1,2) ∙14 = 14…16,8 = 12мм.
Расстояние от внутренней стенки до радиального торца вращающейся детали:
е2
= (0,5…1,0) ∙ δ
= (0,5…1,0) ∙14 = 7,0…14 = 10мм.
Расстояние от окружности выступов наибольшего колеса до дна редуктора: b
0
= (0,5…10)m
= (5…10) ∙8 = 50…80мм.
Размеры отверстий под подшипники редуктора принимаем в зависимости от размеров подшипника, согласно рекомендаций с. 141, [1].
Оставшиеся необходимые геометрические размеры корпуса и крышки принимаем конструктивно на основе рекомендаций с. 140-8. Эскизная компоновка редуктора
8. Выбор шпонок и их проверочный расчет
Выполняем проверочный расчет шпонки на смятие. Результаты расчетов сводим в таблицу 8.2.
Таблица 8.2.
Результаты проверочных расчетов шпонок на смятие
Схема шпоночного соединения

Рис. 8.1.
Для передачи крутящего момента зубчатые колеса, шкивы, муфты соединяются с валами при помощи призматических шпонок.
Геометрические размеры поперечных сечений (b, h) призматических шпонок выбираем в зависимости от диаметров валов. Длины шпонок принимаем на 5…10 мм
меньше длин ступиц в ряду стандартных значений, приведенных в табл.5.19, [1].
В качестве материала шпонок используем – Сталь 45, нормализованную [σзм
] = 140 МПа
и [τзр
] = 100 МПа, с.
191, [1].
Размеры сечений шпонок и пазов по ГОСТ 10748-79 выбираем из табл. 5.19, [1] и сводим в таблицу 8.1
Таблица 81
Параметры и размеры шпоночных соединений
| Номер вала и название шпонки |
Диам. вала d1 мм |
Мкр,
Нм
|
Размеры шпонки, мм |
| b |
h |
l |
t1 |
t2 |
| 2– шпонка под ведомый шкив клиноременной передачи |
50 |
458,5 |
18 |
11 |
80 |
7 |
4,4 |
| 2- шпонка под шестерню цилиндрической передачи I ступени |
55 |
458,5 |
20 |
12 |
90 |
7,5 |
4,9 |
| 3 – шпонка под колесо цилиндрической передачи I ступени |
75 |
1740 |
22 |
14 |
100 |
9 |
5,4 |
| 3 – шпонка под шестерню цилиндрической передачи II ступени |
75 |
1740 |
22 |
14 |
100 |
9 |
5,4 |
| 4 – шпонка под колесо цилиндрической передачи II ступени |
130 |
6542 |
36 |
20 |
180 |
12 |
8,4 |
| 4 – шпонка под зубчатую муфту |
110 |
6542 |
32 |
18 |
150 |
11 |
7,4 |
При эскизном проектировании размещаем детали передач (шестерни и зубчатые колеса), валы, подшипники, складываем эскизную компоновку цилиндрического редуктора.
По определенном размерам зубчатых передач, валов, корпуса и крышки(см. разд. 3, 4, 5, 6,) строим на миллиметровой бумаге формата А1 эскиз коническо – цилиндрического редуктора, в масштабе 1:4. При оформлении эскиза редуктора вычерчиваем конструкцию колес и его корпуса. Подшипники и болтовые соединения вычерчиваем упрощенно.
Подшипники качения выбираются из [3], ориентируясь на диаметры валов и характер нагрузки в передачах. В нашем случае выбираем подшипники №7312, №7314, №7224. В зависимости от их номера, который вмещает сведения о типе и серии подшипника выписываем габаритные размеры, которые используем в эскизной компоновке.
Размеры крышек под подшипники редуктора принимаем в зависимости от размеров подшипников, согласно рекомендаций с. 14.1, [1].
Другие необходимые геометрические размеры принимаем конструктивно, на основе рекомендаций с. 140-143, [1].
Для расчетов промежуточного вала из компоновочного чертежа прямым измерением определяем расстояние между точками приложения сил: l
1
= 108мм,
l
2
= 184мм
иl
3
= 156мм
.
После согласования параметров редуктора, проверочных расчетов валов и подшипников качения, чертим общий вид 143, [1].проверочный расчет шпонок на срез. Результаты вносим в таблицу 8.3.
Таблица 8.3
Результаты проверочного расчета шпонок на срез
Условия прочности на деформации смятия и срез выполняются.
Порядок построения сил выполняем в следующей последовательности:
- вычерчиваем кинематическую схему привода;
- обозначаем опоры валов латинскими буквами А, В, С, D, E, F, обозначаем точки приложения сил К1
, К2
, К3
, К4
, приводим пространственную систему координат X, Y, Z к которой осуществляется привязка действующих сил;
- выполняем построения схемы сил в точках их приложения, способность и долговечность

9. Расчёт промежуточного вала редуктора на статическую способность и долговечность
9.1 Расчет вала на несущую способность
Силы, действующие на вал во время работы редуктора:
- силы, действующие на цилиндрическую шестерню II ступени: окружная сила Ft
ш
= 20470 Н,
Радиальная сила Fr
ш
=7928 Н;
Осевая сила Fa
ш
=7450 Н.
- силы, действующие на цилиндрическое колесо I ступени Ftk
= 8651 Н;
радиальная сила Frk
= 3349 Н;
осевая сила F
ак
= 3139 Н.
Вычерчиваем расчетную схему вала (рис.9.1) и определяем размеры между опорами и точками приложения сил (расстояние определяем по первой эскизной компоновке редуктора измерением, допустив, что силы приложенные по середине колеса и шестерни): l
1
= 108 мм,
l
2
= 184 мм
,l
3
= 156 мм.
Находим реакции в опорах от сил в вертикальной и горизонтальной плоскости:
- в вертикальной х
0у
ΣМ
F
(
D
)
=0.
 . .

RDX
= RCX
–
Fr
ш
+
Frk
= 7262 - 7928 + 3349 = 2683 Н
- в горизонтальной z
Ox
ΣМ
F
(
D
)
=0
ΣМ
F
(
D
)
= - Ft
ш
∙(
l
1
+
l
2
)+
Ftk
∙
l
1
+
Rc
z
(
l
1
+
l
2
+
l
3
) = 0

RDZ
= - Rc
z
+
Ft
ш
+
Ftk
= - 11256 + 20470 – 8651 = 562Н
Выполняем построения эпюр моментов изгиба в вертикальной и горизонтальной плоскостях, суммарного крутящего момента и изгиба.
Момент изгиба в вертикальной плоскости:
в m.K3
: МК3
= RDX
· l
1
=2683 · 0,108 = 290 Нм;
в m.K4
: МК4
= RCX
· l
3
=7262 · 0,156 = 1132,8 Нм;
Момент изгиба в горизонтальной плоскости
в m.K4
: МК4
= RDz
· l
1
=
562 · 0,108 = 61Нм;
Суммарный момент изгиба определяется по формуле:
в m.K3
: 
в m.K4
: 
Определяем приведенный (эквивалентный) момент в опасном сечении.
Исходя из анализа построенных эпюр моментов опасное сечение вала находится на шестерне цилиндрической передачи II ступени (точка К4
).
Значение эквивалентного момента в m.K4
:
 . .

– коэффициент, табл. 5.3., [1] для материала вала
– сталь 40. [σ1
], σ0
- допустимые напряжения для материала вала соответственно при симметричном и при пульсирующем циклах нагрузки, табл. 5.3., [1].

Определяем диаметр вала в опасном сечении:

Полученный диаметр округляем до ближайшего большего значения из стандартного ряда R
а
40 ГОСТ 6636-69.
С учетом шпоночного паза принимаем d
32
= 75мм.
Диаметр вала в этом сечении, принятый в условном расчете
d
32
= 75,0мм,
т.е. условие выполняется.
9.2 Расчет вала на прочность
Для опасного сечения быстроходного вала, который имеет конструктивный концентратор напряжений – переход от меньшего диаметра к большему (между участками под подшипник и шестерню), определяем характеристики напряжений, [1], с.173- 185.
- границы выносливости:
для напряжений изгиба при симметричном цикле:
σ
-1
= 043σВ
=0,43 · 800 = 344 МПа, σ
m
= 0 МПа;
для напряжений кручения при пульсирующем цикле:
τ-1
= 0,58 σ
-1
= 0,58 · 344 = 199,52 МПа; τm
= τа
=2,79 МПа;
-амплитуды напряжений:
при симметричном цикле:

где МЗ
j
– суммарный момент изгиба в m. К4
, Нм,

Рис. 11 .1.
З
j
– осевой момент в сечении опор j
– того участка вала. Для сечения в m. К4
, м3
.

где d –
диаметр вала под подшипник,
при пульсирующем цикле:

где W
к
j
– полярный момент сечения опор j
– того участка вала. Для сечения под шпонку, м3
.

Выбираем коэффициенты:
- эффективные коэффициенты конструкционных напряжений при изгибе - Кσ
= 1,75, при кручении - Кτ
=1,50, табл. 5.11, [1].
- масштабные коэффициенты, учитывающие снижения границы выносливости с увеличением размеров вала: при изгибе - έσ
= 0,745; при кручении- έ
r
= 0,745, табл. 5.16, [1].
- коэффициенты учитывающие свойства материалов до асимметрии цикла напряжений:
при изгибе – ψσ
=0,02 + 2·10-4
· 800 = 0,18 МПа;
при кручении - ψτ
=0,5ψσ
= 0,5· 0,18 = 0,09 МПа.
Определяем коэффициент запаса прочности опасного сечения:

где Ѕσ
и Ѕτ
– коэффициенты запаса прочности при действии изгиба и кручения.
[Ѕ
] –
допустимое значениекоэффициенты запаса прочности. Для редукторных валов [Ѕ
] ≥2,5…3,0, с.185, [1].
 , ,
 , ,

Условие выполняется.
10. Расчет подшипников качения
Исходные данные для расчета:
Диаметры вала под подшипники – 70 мм
Реакции в опорах: Rсх
= 7262 Н,
R
DX
=2683Н,
RCZ
=
11256,
ROZ
=
562H
Осевые силы: F
фш
= 7450 Н,
F
ок
= 3139Н.
Угловая скорость: ω3
=
18,3 рад/с.

Pис. 12.1
10.1 Определение реакции в опорах
Определяем результативную радиальную реакцию в каждой опоре вала (для схемы нагрузки):
 , ,
где Rпх
= R
nz
–
радиальные реакции в опоре, в горизонтальной и вертикальной плоскостях.
Индекс «п»- опора.
 ; ;
 . .
Выбираем роликовые однорядные подшипники №7314 с такими основными параметрами:
d
= 70 мм, D
= 150 мм, B
= 35 мм
.
C
= 168 кН
– динамическая грузоподъемность;
С0
= 137 кН
– статическая грузоподъемность;
е
= 1,5tga
=1,5 tg
140
= 0,37.
Результирующая осевая сила:
F
a
= Fаш
Fак
=
7450 –3139=
1713 Н.
Определяем по соотношению  коэффициент осевой нагрузки. коэффициент осевой нагрузки.
Определяем составляющие осевых реакций Sп
в подшипниках от радиальных реакций Rrn
:для радиально-упорных шариковых подшипников:
- для опоры А:
SC
=
eRrC
=0.37∙13395=4956H
;
для опоры В:
SD
=
eRrD
=
0.37∙2741=1014.0
H
.
Определение осевых реакций R
ап
подшипников.
Осевые реакции определяем исходя из схемы размещения подшипников, принимаем схему – «в распор»:

Рис.10.2.
-в т. D
ΣF
=-
SC
+
Fa
+
SD
=-4956+4311+1014=369H
>0.
тогда
RaD
=
Fa
+
SC
=
4311+4956=9267H
-в т. С
Σ
F
=-
SD
-
Fa
+
SC
=-
1014-4311+4956=-369H
.>0
тогда
RaC
=
SC
=
4956H
.
10.2 Определение коэффициентов
V
-коэффициент оборота кольца, V
=
1,0 (вращается внутреннее кольцо);
реакции подшипников:
- для опоры С

- для опоры D

10.3 Определение эквивалентной нагрузки
Pen
=(
X
∙
V
∙
Rrn
+
Y
∙
Ran
)∙
Kσ
KT
:
- опора С: РеС
=(1∙1∙13395+0∙4956)∙1,3∙1,0=17413,5Н
;
- опора D: PeD
=(0.4∙1∙2741+1.88∙9267)∙1.3∙1.0=24074H
.
10.4 Определяем долговечность подшипников
 , ,
где пi
- частота вращения i-того вала, об/мин,
 . .
р=10/3- для роликовых подшипников.
Опора С:  ч, ч,
Опора D:  ч, ч,
Срок работы привода Lh
=1∙104
ч подшипники (опора С и опора D) обеспечивают.
10.5 Выбор муфты
Расчётный крутящий момент, который передаёт муфта в данном приводе определяется по формуле:
М
max
=
KP
M
н
=1,5∙6682=10023Нм,
где KP
= 1,5 – коэффициент, который учитывает условия эксплуатации установки, принимаем по табл. 7.1. , [1].
Мн
– номинальный крутящий момент на валу.
Выбираем зубчатую муфту МЗ 6, табл. 17.6.,[9] с такими параметрами:
М=11800 Нм
, d
в
= 105 мм,
nmax
=2500 об/мин.
Геометрические размеры муфты, см. рис. 12.2.
B
= 50 мм,
D
=320 мм,
D
1
=230 мм,
D
2
=140 мм,
L
=255 мм.
Размеры зацепления зубчатой муфты:
m
=4,0 мм,
z
=48,
b
=30 мм.
Муфты зубчатые используют для соединения валов, которые передают большие крутящие моменты, где точное установление валов невозможно или возникают значительные осложнения. Зубчатые муфты отличаются компактностью и высокой выносливостью нагрузок.
Компенсирующая способность муфты достигается созданием зазоров между зубьями и приданием бочкообразной формы зубьям.
10.6 Проверочный расчёт зубчатой муфты

Рис. 10.5.
11. Выбор и проверочный расчёт опор скольжения
В качестве опор конвейера принимаем подшипники скольжения, разъёмные с двумя болтами по ГОСТ 11607-65 с чугунными вкладышами с СЧ 18 для которого определяем допустимые значения параметров:  , ,  , табл. 9.1, [8]. , табл. 9.1, [8].
Конструктивные размеры корпуса выбранного подшипника определяем согласно С.594, [8] в зависимости от диаметра вала:
d
В
=110 мм
, d
1
=32 мм
, B
=130 мм,
b
=110 мм
, H
=200 мм
, h
=
110 мм
, h
1
= 40 мм,
L
=370 мм
, A
=310 мм
,
A
1
=
190 мм
, шпилька
М24х100.
Схема подшипника скольжения

Рис. 11.1.
Проверяем выбранный подшипник по двум критериям:
- условие износа ( долговечность )
 , ,
где F
0
=
Ft
=28000 H
– окружная сила, см. раздел 1.1.
- условие теплоустойчивости

где  - скорость скольжения. - скорость скольжения.
Оба условия выполняются, значит опоры скольжения удовлетворяют
При проверочном расчёте у зубчатых муфт рассчитывают рабочие поверхности зубов на износ (определяется граничное значение удельного давления на зубцы муфты).

где d
0
– диаметр делительного круга, м,
d
0
=
mz
=
4,0∙48=192 мм,
b
– длина зуба зубчатой втулки, м,
[q] – допустимое значение удельного давления для материала зубов, МПа
, табл. 17.6, [9].
Литература
1. Киркач Н.Ф., Баласанян Р.А.. Расчёт и проектирование деталей машин [Учеб. Пособие для техн. вузов]. – 3-е изд., перераб. и доп. – Х.: Основа,1991.- 276 с.: схем.
2. Расчёты деталей машин: Справ. Пособие / А.В. Кузьмин, И.М. Чернин, Б.С. Козинцов. – 3-е изд., перераб. и доп. – Мн.: Выс. шк., 1986. – 400 с.: ил.
3. Курсовое проектирование деталей машин: Справ. Пособие. Часть 1 / А.В. Кузьмин, Н.Н. Макейчик, В.Ф. Калачев и др.-Мн.: Выс. школа ,1982-208 с.,ил.
4. Курсовое проектирование деталей машин: Справ. Пособие. Часть 2 / А.В. Кузьмин, Н.Н. Макейчик, В.Ф. Калачев и др.-Мн.: Выс. школа ,1982-334 с.,ил.
5. Методичні вказівки для виконання курсового проекту з курсу „Деталі машин” (Розділ „Пасові передачі ”) для студентів спец. 31.11 заочної форми навчання / Гончарук О.М., Стрілець В,М., Шинкаренко І.Т., - Рівне, У||ВГ, 1990.-24 с.
6. Методические указания по выполнению курсового проекта по курсу «Детали машин» (Раздел «Расчёт закрытых зубчатых и червячных передач») для студентов специальности 1514 заочной формы обучения / Стрелец В.Н,, Шинкаренко И,Т.- Ровно, УИИВГ, 1988 – 41 с.
7. Методичні вказівки для виконання курсового проекту з курсу „Деталі машин” (Розділ „Розрахунки валів і підшипників кочення”) для студентів спец. 31.11 заочної форми навчання / Стрілець В,М., Шинкаренко І.Т., - Рівне, У||ВГ, 1990.-16 с.
С.А. Чернавский, Г.М. Ицкович и др.. Курсовое проектирование деталей машин, М: Машиностроение, 1979-351
|