Постановка задачі оптимального керування
1. Об’єкт керування
Розглянемо систему (об’єкт керування), поведінка якої характеризується двома видами параметрів – параметрами стану та параметрами керування.
Керована система – це система, що функціонує під впливом певного фактора, який здатний регулювати її еволюцію.
Як правило, існує безліч способів керування об'єктом з метою переведення системи в заданий стан. У зв'язку із цим виникає задача знайти такий спосіб керування, що у певному розумінні є оптимальним. При цьому система може зазнавати випадкових впливів. Для того, щоб вибирати із усіх можливих способів керування найкращий, необхідно визначити критерій якості.
Якщо еволюція системи за заданих початкових умов однозначно визначається завданням керування в кожний момент часу і не залежить від випадкових зовнішніх впливів, то система називається детермінованою.
Стан динамічного об'єкта у фіксований момент часу описується набором параметрів  , …, , …,  , які називаються фазовими координатами (фазовими змінними), а вектор , які називаються фазовими координатами (фазовими змінними), а вектор  називається фазовим вектором. Стан об'єкта в будь-який момент часу задається точкою називається фазовим вектором. Стан об'єкта в будь-який момент часу задається точкою  -вимірного простору -вимірного простору  , що називається фазовим простором. Величини , що називається фазовим простором. Величини  , …, , …,  залежно від контексту задачі визначають координати об'єкта, швидкість об'єкта та ін. залежно від контексту задачі визначають координати об'єкта, швидкість об'єкта та ін.
Рух об'єкта супроводжується зміною його фазових координат у часі  , тобто фазовий вектор є функцією змінної , тобто фазовий вектор є функцією змінної  : :  . .
Під час руху фазова точка 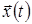 описує у фазовому просторі криву, що називається фазовою траєкторією. описує у фазовому просторі криву, що називається фазовою траєкторією.
Сукупність усіх фазових станів, у яких може перебувати керований об'єкт, складає множину станів  простору простору  . Таким чином, у будь-який момент часу повинні виконуватися обмеження на фазові координати: . Таким чином, у будь-який момент часу повинні виконуватися обмеження на фазові координати:
 : :  .(1) .(1)
Множина фазового простору, що включає ті фазові стани, які є бажаними з точки зору цілей керування даним об’єктом, називається множиною мети керування  , ,  . .
Керування об'єктом у кожний момент часу задається вектором керування  , ,  , де , де  , …, , …,  – параметри керування. – параметри керування.
У загальному випадку стан об'єкта в будь-який момент часу  залежить від того, яким було керування залежить від того, яким було керування  до моменту часу до моменту часу  і не залежить від майбутнього керування. і не залежить від майбутнього керування.
У реальних об'єктах керування не може бути довільним, що пов'язано або з конструктивними особливостями об'єкта, або з обмеженістю ресурсів, або з умовами експлуатації об'єкта. У просторі керування  (просторі всіх можливих керувань) виділяється деяка множина (просторі всіх можливих керувань) виділяється деяка множина  , що називається множиною припустимих керувань і містить сукупність тих функцій , що називається множиною припустимих керувань і містить сукупність тих функцій
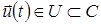 , ,  ,(2) ,(2)
які, виходячи з умов задачі, можуть бути обрані за керування даною системою серед всіх можливих функцій керування. У прикладних задачах, як правило, область керування  є обмеженою замкнутою множиною. є обмеженою замкнутою множиною.
Найчастіше за керування обирають кусково-неперервні вектор-функції, для яких кожна координата  має на будь-якому кінцевому інтервалі скінченне число точок розриву першого роду має на будь-якому кінцевому інтервалі скінченне число точок розриву першого роду  , причому для визначеності припускають, що , причому для визначеності припускають, що
 , ,  , ,
і, крім того, керування  неперервно на кінцях відрізка неперервно на кінцях відрізка  . .
Кусково-неперервні керування  , такі що , такі що  , називаються припустимими. , називаються припустимими.
Припустимим процесом називається пара функцій  , де , де  – припустиме керування, а – припустиме керування, а 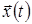 – відповідна йому фазова траєкторія. – відповідна йому фазова траєкторія.
Детермінованість керованого об'єкта означає, що вибір керування  , ,  за заданих початкових умов однозначно визначає траєкторію руху за заданих початкових умов однозначно визначає траєкторію руху 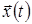 , ,  . .
Існує два підходи для визначення оптимального керування. Перший полягає в тому, що оптимальне керування будується як функція часу  . Таке керування називається програмним керуванням. Із прикладної точки зору такий підхід є недосконалим, тому що не враховує впливів на систему зовнішніх факторів. . Таке керування називається програмним керуванням. Із прикладної точки зору такий підхід є недосконалим, тому що не враховує впливів на систему зовнішніх факторів.
Другий підхід полягає в тому, що оптимальне керування будується як функція фазових координат, тобто  . Таке керування називають синтезуючим (або позиційним), а відповідну задачу – задачею синтезу оптимальних керувань. Таке керування враховує поточний стан системи, але його пошук значно складніший порівняно з пошуком програмного керування. . Таке керування називають синтезуючим (або позиційним), а відповідну задачу – задачею синтезу оптимальних керувань. Таке керування враховує поточний стан системи, але його пошук значно складніший порівняно з пошуком програмного керування.
Характер зміни фазової траєкторії об'єкта у часі задається законом руху. У теорії детермінованого керування найчастіше розглядаються динамічні системи за законом руху у формі диференціальних рівнянь
 .(3) .(3)
Тут  – вектор-функція, компоненти якої неперервні по всій сукупності змінних і неперервно диференційовані по змінних – вектор-функція, компоненти якої неперервні по всій сукупності змінних і неперервно диференційовані по змінних  . Отже, якщо відоме керування . Отже, якщо відоме керування  , ,  , то траєкторія об'єкта , то траєкторія об'єкта 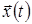 може бути визначена як розв’язок диференціального рівняння може бути визначена як розв’язок диференціального рівняння
 . .
Якщо для функції  виконуються перераховані вище умови, то остання система задовольняє теоремі існування та єдиності розв’язку для задачі Коші, тобто за заданих початкових умов виконуються перераховані вище умови, то остання система задовольняє теоремі існування та єдиності розв’язку для задачі Коші, тобто за заданих початкових умов  вона має єдиний розв’язок в околі точки вона має єдиний розв’язок в околі точки  . .
Задача керування рухом полягає в тому, щоб відшукати припустиме керування, яке реалізує ціль. Це означає, що потрібно відшукати таку кусково-неперервну функцію  , визначену на відрізку , визначену на відрізку 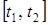 , для якої система (3) має розв’язок , для якої система (3) має розв’язок 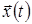 , який задовольняє початковій умові , який задовольняє початковій умові  , обмеженню , обмеженню  і кінцевій умові і кінцевій умові  . Отже, задача детермінованого керування зводиться до розв’язання крайової задачі для системи . Отже, задача детермінованого керування зводиться до розв’язання крайової задачі для системи  -го порядку (3) за заданих обмежень (1) і (2). -го порядку (3) за заданих обмежень (1) і (2).
2. Крайові умови задачі оптимального детермінованого керування
Якщо множина мети керування  збігається з усім фазовим простором збігається з усім фазовим простором  , то задача оптимального керування називається задачею з вільним кінцем траєкторії. У цьому випадку роль крайових умов відіграють початкові умови , то задача оптимального керування називається задачею з вільним кінцем траєкторії. У цьому випадку роль крайових умов відіграють початкові умови 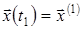 . .
2. Якщо задані початкові 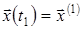 і кінцеві умови і кінцеві умови 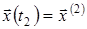 , то задача оптимального керування називається двоточковою задачею або задачею з фіксованими кінцями. При цьому інтервал часу керування , то задача оптимального керування називається двоточковою задачею або задачею з фіксованими кінцями. При цьому інтервал часу керування  може бути заданий або підлягає визначенню. Для даної задачі множина мети керування може бути заданий або підлягає визначенню. Для даної задачі множина мети керування  складається з єдиної точки складається з єдиної точки 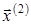 . .
3. Якщо значення координат (всіх або частини) вектора стану 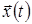 задані для декількох фіксованих моментів часу задані для декількох фіксованих моментів часу 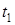 , ,  , …, , …,  , то задача оптимального керування називається багатоточковою задачею керування. , то задача оптимального керування називається багатоточковою задачею керування.
4. У задачах з рухомими кінцями необхідно визначити керування, що переводить об'єкт із деякого заздалегідь невідомого стану  в деякий стан в деякий стан  , де множини , де множини  , ,  відомі. Якщо відомі. Якщо  і і  вироджуються в точки, то задача оптимального керування стає задачею із фіксованими кінцями. вироджуються в точки, то задача оптимального керування стає задачею із фіксованими кінцями.
Якщо час 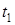 і і  початкових і кінцевих крайових умов початкових і кінцевих крайових умов  і і  відомий, то задача оптимального керування називається задачею з фіксованим часом. Якщо ж відомий, то задача оптимального керування називається задачею з фіксованим часом. Якщо ж  невідомо, то задача називається задачею з вільним часом. невідомо, то задача називається задачею з вільним часом.
3. Критерії якості
Найчастіше задача керування має безліч розв’язків, тобто існує безліч керувань, які дозволяють досягти бажаної мети. У такому випадку виникає задача, як серед всіх припустимих керувань вибрати таке, для якого керований процес буде, в певному розумінні, найкращим. Інакше кажучи, якщо якість процесу можна оцінити деякою числовою характеристикою  – критерієм якості, то задача полягає у виборі такого керування, що забезпечить його оптимальне значення. Далі вважатимемо, що оптимальним є мінімальне значення критерію – критерієм якості, то задача полягає у виборі такого керування, що забезпечить його оптимальне значення. Далі вважатимемо, що оптимальним є мінімальне значення критерію  . Отже, задача оптимального керування полягає в тому, щоб визначити таке керування . Отже, задача оптимального керування полягає в тому, щоб визначити таке керування
 , що реалізує ціль, і для якого функціонал , що реалізує ціль, і для якого функціонал  набуває найменшого можливого значення: набуває найменшого можливого значення:
 .(4) .(4)
Процес  з (4) називається оптимальним процесом, а відповідні йому керування з (4) називається оптимальним процесом, а відповідні йому керування  і фазова траєкторія і фазова траєкторія  – оптимальним керуванням і оптимальною траєкторією. – оптимальним керуванням і оптимальною траєкторією.
Припустимий процес  називається локально оптимальним у задачі з фіксованим часом називається локально оптимальним у задачі з фіксованим часом 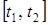 , якщо для певного , якщо для певного  і для будь-якого припустимого процесу і для будь-якого припустимого процесу  , що задовольняє умові , що задовольняє умові
 , ,  , ,
має місце нерівність  . .
Якщо відрізок 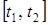 не фіксований, то локально оптимальним процесом називається припустимий процес не фіксований, то локально оптимальним процесом називається припустимий процес  на інтервалі часу на інтервалі часу  , для якого існує таке , для якого існує таке  , що для будь-якого процесу , що для будь-якого процесу  , заданого на інтервалі часу , заданого на інтервалі часу 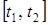 , такого що , такого що
 , ,  , ,  , , 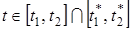 , ,
має місце умова  . .
Існують такі типи критеріїв якості.
Для керування процесами (3) найчастіше використовуються інтегральні критерії:
 .(5) .(5)
Інтегральні критерії розділяються на:
а) інтегральний критерій оптимальної швидкодії:

з підінтегральною функцією 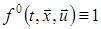 ; ;
б) інтегральний квадратичний критерій з підінтегральною функцією
 , ,
де  ; ;
 , ,  – коефіцієнти, серед яких є хоча б один ненульовий. – коефіцієнти, серед яких є хоча б один ненульовий.
Вивчення системи може проводитися як на скінченному, так і на нескінченному інтервалі часу, тому в інтегралі (5)  ; ;
в) енергетичні критерії якості з підінтегральними функціями
 або або  , ,
де  ; ;
 , ,  – коефіцієнти, серед яких хоча б один ненульовий; – коефіцієнти, серед яких хоча б один ненульовий;
г) змішаний інтегральний критерій з підінтегральною функцією
 . .
2. Термінальні критерії якості:
 , ,
наприклад, критерій кінцевого стану:
 . .
Даний критерій використовують, якщо необхідно привести систему в заданий кінцевий стан  у момент часу у момент часу  з мінімальною помилкою. У цьому випадку критерій кінцевого стану матиме вигляд з мінімальною помилкою. У цьому випадку критерій кінцевого стану матиме вигляд
 . .
3. Змішані критерії якості:
 , ,
які можна привести до інтегрального вигляду:
 . .
4. Задачі з дискретним часом
Дотепер ми розглядали процеси з неперервним часом, наприклад, процеси з законом руху у вигляді систем диференціальних рівнянь. Іноді важливими є лише значення станів системи в деякі дискретні моменти часу, або сам метод розв’язання потребує зробити дискретизацію задачі, тобто замінити диференціальні рівняння різницевими. У обох цих випадках використовують системи різницевих рівнянь вигляду
 , ,  , ,
або
 ,(6) ,(6)
де  , а , а  – число кроків дискретизації процесу. – число кроків дискретизації процесу.
Початкові та кінцеві умови для задачі (6) мають вигляд:
 , ,  .(7) .(7)
Аналоги інтегрального та термінального критеріїв якості для процесу (6) мають наступний вигляд.
1. Необхідно визначити такі вектори  , ,  , …, , …,  і і  , ,  , …, , …,  , на яких величина , на яких величина

набуває мінімального значення за умов (6), (7).
2. Необхідно визначити такі вектори  , ,  , …, , …,  і і  , ,  , …, , …,  , на яких величина , на яких величина

набуває мінімального значення за умов (6), (7).
5. Основні питання теорії оптимального керування
1. Керованість. Перед розв’язанням задачі оптимального керування необхідно з'ясувати питання про те, чи існує хоча б одне припустиме керування  , що переводить динамічний об'єкт із множини початкових станів , що переводить динамічний об'єкт із множини початкових станів  у множину кінцевих станів у множину кінцевих станів  , тобто чи існує таке припустиме керування , тобто чи існує таке припустиме керування  , для якого вектор фазових станів , для якого вектор фазових станів 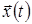 задовольняє початковим і кінцевим умовам. Якщо таке керування існує, то об'єкт називається керованим із множини задовольняє початковим і кінцевим умовам. Якщо таке керування існує, то об'єкт називається керованим із множини  у множину у множину  . Інакше розв’язування задачі не має сенсу. . Інакше розв’язування задачі не має сенсу.
2. Існування оптимального керування. Якщо об'єкт керований, виникає питання про те, чи існує оптимальне керування. З математичної точки зору воно має важливе значення, оскільки математика працює з моделями реальних об'єктів, а відсутність у моделі оптимального керування може вказувати на те, що сама модель побудована невірно.
3. Необхідні умови оптимальності. Навіть у простих задачах може виявитися безліч припустимих керувань, які переводять систему із множини початкових станів у множину кінцевих станів (за умови, що оптимальне керування існує). Тому розв’язувати задачу оптимального керування перебором усіх можливих варіантів найчастіше неефективно. Виділити із усієї множини припустимих керувань підозрілі на оптимальність можна за допомогою необхідних умов оптимальності. Отже, задача пошуку оптимального керування зводиться до його пошуку серед тих керувань, які задовольняють необхідним умовам оптимальності, наприклад, принципу максимуму Понтрягіна.
4. Достатні умови оптимальності. Навіть у випадку використання необхідних умов оптимальності клас підозрілих на оптимальність керувань часто залишається досить широким. Вибрати з нього дійсно оптимальні керування можна за допомогою достатніх умов оптимальності. Якщо деяке керування із класу підозрілих на оптимальність задовольняє достатнім умовам оптимальності, то це гарантує його оптимальність. Можуть існувати задачі, у яких достатнім умовам задовольняють відразу кілька керувань. У цьому випадку вони всі є оптимальними.
5. Єдиність оптимального керування. Важливе значення має питання про те, чи є отримане оптимальне керування єдиним, тому що в цьому випадку може значно спроститися його реалізація для реальних керованих об'єктів.
|