Предмет:
Статистическая динамика систем автоматического управления
тема:
Прохождение случайного сигнала через дискретную и нелинейную систему. Прохождение случайного сигнала через дискретную систему
Рассмотрим дискретную систему, схема которой представлена на рис.1.
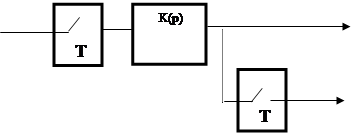 x y x y
Rxx(t) Ryy[nT]
Sxx(w) S*yy(w)
Рис. 1
Корреляционная функция выхода равна
 (1) (1)
где (2N+1) - число отсчетов. Определим соотношения для спектральных плотностей входного и выходного сигнала. Выполним дискретное преобразование Фурье

С учетом

получим выражения для спектральных плотностей
 (2) (2)
Корреляционные функции равны:
 (3) (3)
Статистические характеристики сигналов в дискретных системах
Для дискретных систем можно использовать методы статистической динамики, разработанные для непрерывных систем с учетом некоторых особенностей.
Основной временной характеристикой непрерывной системы при случайных воздействиях является корреляционная функция
 (4) (4)
Для дискретных систем она представляет решетчатую функцию
 (5) (5)
Среднее квадратичное отклонение или дисперсия
 (8.6) (8.6)
Преобразования Фурье для непрерывных и дискретных систем
 (7) (7)
Примеры решений задач
Пример 1. Для заданной спектральной плотности непрерывного сигнала определить дискретную спектральную плотность
 . Определить . Определить  . .
Решение:
1. Для заданной спектральной плотности определим корреляционную функцию
 
2. Определим дискретную корреляционную функцию

3. Определим дискретную спектральную плотность

4. Определим дискретную спектральную плотность в форме z -
преобразования, выполнив подстановку z = epT
.

Проверка: Определим дискретную корреляционную функцию

Спектральная плотность равна
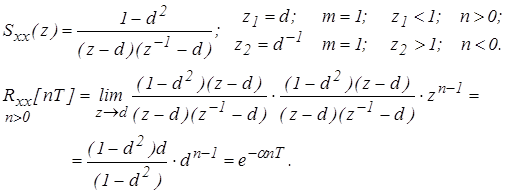
Так как корреляционная функция является четной то

Пример 2. Определить дискретную спектральную плотность  и корреляционную функцию и корреляционную функцию выходного сигнала для заданной системы (рис.3), если спектральная плотность входного сигнала имеет вид выходного сигнала для заданной системы (рис.3), если спектральная плотность входного сигнала имеет вид
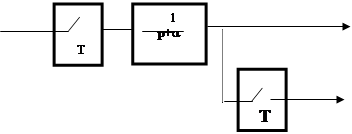 x y x y
Rxx(t) Ryy[nT]
Sxx(w) S*yy(w)
Рис. 3
Решение:
Для заданной

передаточная функция дискретной системы равна

Определим дискретную спектральную плотность и корреляционную функцию выхода
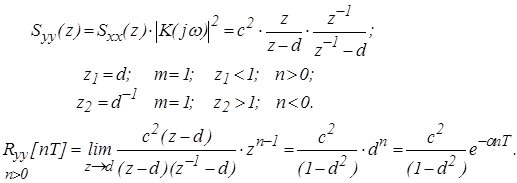
Аналогично определим дискретную корреляционную функцию выхода для левой ветви

Так как корреляционная функция является четной, то

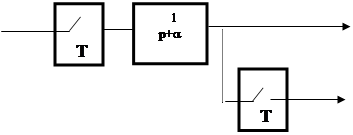
Пример 3. Определить дискретную спектральную плотность  и корреляционную функцию и корреляционную функцию выходного сигнала для заданной системы (рис.4), если корреляционная функция входного сигнала имеет вид выходного сигнала для заданной системы (рис.4), если корреляционная функция входного сигнала имеет вид

 x y x y
Rxx(t) Ryy[nT]
Sxx(w) S*yy(w)
Рис. 4
Решение: Определим дискретную передаточную функцию

Для заданной корреляционной функции входного сигнала дискретная спектральная плотность равна:

Определим дискретную спектральную плотность и корреляционную функцию выхода
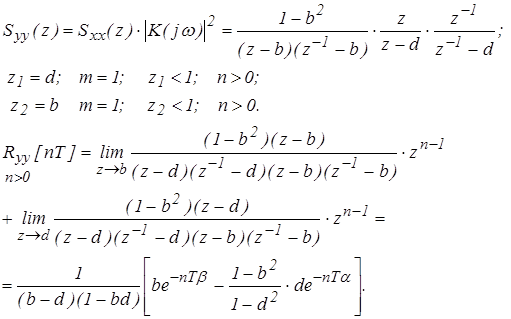
Так как корреляционная функция является четной то

Пример 4. Определить дискретную спектральную плотность  для заданной системы (рис.5), если корреляционная функция входного сигнала имеет вид для заданной системы (рис.5), если корреляционная функция входного сигнала имеет вид 
 x u y x u y
 _ _
Rxx(t) Ryy[nT]
Sxx(w) S*yy(w)
Рис.5
Решение: Спектральная плотность равна

Пример 5. Для заданной системы (Рис.6) определить , если , если  а алгоритм функционирования цифровой части описывается уравнением: а алгоритм функционирования цифровой части описывается уравнением:

 x y x y
-
Рис.6
Решение: В соответствии с алгоритмом функционирования цифровой части запишем его передаточную функцию

Исходную сему можно представить в виде (рис.7)
Рис.7Определим передаточную функцию разомкнутой системы


Определим передаточную функцию замкнутой системы

Спектральной плотности непрерывного сигнала

соответствует дискретная спектральная плотность (см. пример 1)

Спектральная плотность выходного сигнала равна:

Прохождение случайного сигнала через нелинейную систему
В статистической динамике линейных систем используются методы усреднения по времени (корреляционные функции и спектральные плотности), в статистической динамике нелинейных систем используют методы усреднения по множеству (законы распределения).
Рассмотрим нелинейное безинерционное звено с заданной характеристикой z =
j (x),
на вход которого подается случайный сигнал x (t)
с заданным законом распределения f (x) (
рис.8)Определить закон распределения f (z).
Допустим, характеристика нелинейного элемента является монотонной, а плотность вероятности с нормальным распределением (рис.9а, б).
а) б)Рис.9
Каждому значению x
соответствует определенное значение z
. Рассмотрим некоторую область] x1
, x1
+
dx [
P (x1
< X < x1
+ dx) = f (x) dx;
P (z1
< Z < z1
+ dz) = f (z) dz.
Из условия равенства вероятностей принадлежности сигнала на входе области x1
<
X <
x1
+
dx
и сигнала на выходе области z1
<
Z <
z1
+
dz
можно определить f (
z)
f (x) dx = f (z) dz; f (z) =f (x) dx/dz.
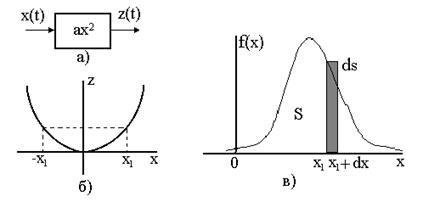
Рис.10
Пример 9.1. На вход нелинейного звена с заданной характеристикой поступает случайный сигнал с симметричным нормальным распределением (рис.10). Определить плотность распределения сигнала на выходе звена. Нормальное центрированное (симметричное) распределение имеет вид

Плотность распределения сигнала на выходе звена можно определить из соотношения

При изменении входной величины - ¥ < x
< ¥, выходная величина изменяется в пределах 0 < z
< ¥, т.е. каждому значению x
соответствует два значения z
, поэтому можно записать
 
Если  , то , то  при этом можно записать выражение для плотности распределения на выходе нелинейного звена при этом можно записать выражение для плотности распределения на выходе нелинейного звена

Литература
1. Вероятностные методы в вычислительной технике. Под ред.А.Н. Лебедева и Е.А. Чернявского - М.: Высш. Шк., 1986. - 312 с.
2. Гальперин М.В. Автоматическое управление Изд-во: ИНФРА-М, ИЗДАТЕЛЬСКИЙ ДОМ, 2004с. - 224с.
3. Справочник по теории автоматического управления. /Под ред.А. А. Красовского - М.: Наука, 1987. - 712 с.
4. Теория автоматического управления: Учебник для вузов. Ч1/Под ред.А. А. Воронова - М.: Высш. Шк., 1986. - 367 с.
|