Министерство образования и науки Российской Федерации
Тольяттинский филиал Московского государственного университета пищевых производств
Кафедра Менеджмента пищевых производств
Курсовая работа
по дисциплине «Методы и средства измерений, испытаний и контроля»
на тему «Разработка программы определительных испытаний»
Студентка группы:
Преподаватель:
Тольятти 2008
Содержание
Введение
1 Разработка программы испытаний
1.1Общие положения
1.2 Объект испытаний
1.3 Цель испытаний
1.4 Место проведения и обеспечения испытаний
1.5 Объем и методика испытаний
1.6 Обработка результатов испытаний
1.6.1 Постановка задачи
1.6.2 Вычисление основных характеристик выборки
1.6.3 Формирование статистического ряда и графическое представление данных
1.6.4 Подбор подходящего закона распределения вероятностей
1.6.5 Определение показателей надежности объекта испытаний
1.6.6 Протокол испытаний
2 Пример обработки результатов испытаний для восстанавливаемого объекта испытаний
2.1 Постановка задачи
2.2 Вычисление основных характеристик выборки
2.3 Формирование статистического ряда и графическое представление данных
2.4 Подбор подходящего закона распределения вероятностей
2.5 Определение показателей надежности объекта испытаний
Заключение
Список использованных источников
Введение
Испытанием – это экспериментальное определение количественных и качественных характеристик свойств объекта как результата воздействия на него при его функционировании или моделировании.
Испытания опытных образцов, установочных и первых промышленных партий, контрольные периодические испытания серийной продукции – это основа построения всей системы разработки и постановки продукции на производство.
Постоянное повышение требований к качеству выпускаемой продукции, рост сложности современной техники, создание новых видов продукции с использованием последних достижений науки и техники определили значительное расширение видов испытаний, увеличение их сложности и трудоемкости.
Испытания являются неотъемлемой частью взаимоотношений заказчика и изготовителя продукции, предприятия-изготовителя конечной продукции и предприятий-смежников, поставщика и потребителя при внутреннем и международном товарообмене.
Все испытания по своему назначению разделяют на четыре группы: исследовательские, контрольные, сравнительные и определительные.
Целью данной курсовой работы является определение реального уровня надежности выбранного объекта испытаний – электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40, предназначенный для привода различных бытовых приборов.
1. Разработка программы испытаний
Программа испытаний – это обязательный для выполнения организационно-методический эксперимент.
Программа устанавливает цели испытаний, объект испытаний, объем и методику проводимых экспериментов, порядок, условия, место и сроки проведения испытаний, ответственность за обеспечение и проведение испытаний, ответственность за оформление протоколов и отчетов по испытаниям.
Немаловажную роль в программе испытаний играет план проведения испытаний. В плане указываются работы необходимые для проведения испытаний, изготовления образцов, приемка образцов, измерение и определение параметров образцов объекта испытаний, подготовка испытательного оборудования, оформление результатов испытаний, согласование утверждения протокола испытаний и др.
Основной задачей определительных испытаний является определение характеристик изделия или материала. Существенным является правильно сформулировать цели испытания.
Цель испытания раскрывает его назначение, которое должно отображаться в наименовании испытаний.
1.1 Общие положения
Настоящая программа испытаний составлена на основании следующих нормативно-технических документов:
- ГОСТ 27.410-87 «Методы контроля показателей надежности и планы контрольных испытаний на надежность»;
- ГОСТ 11828-86 «Машины электрические вращающиеся. Общие методы испытаний»;
- ГОСТ 10159—79 «Машины электрические вращающиеся коллекторные. Методы испытаний»
1.2 Объект испытаний
Главным признаком объекта испытаний является то, что по результатам его испытаний принимается то или иное решение, а именно его годность или выбраковывание, предъявление на следующие испытания, возможность серийного выпуска и т.д.
Объектом испытаний является электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40.
Таблица 1 – Габаритные установочные и присоединительные размеры электродвигателей
№
|
Наименование параметра |
Тип двигателя |
| ДК 60 - 40 - 15 УХЛ4 |
| 1 |
Напряжение питания, В |
220±22 |
| 2 |
Частота питания, Гц |
50±1 |
| 3 |
Вращаюший момент, Нхм |
0,026±0,003 |
| 4 |
Частота вращения, об./мин. |
+3000
15000
-1500
|
| 5 |
Ток, А не более |
0,48 |
| 6 |
Коэффициент полезного действия, % |
45 -6,8 |
| 7 |
Масса двигателя, кг не более |
0,35 |
| 8 |
Lmax, мм |
90 |
| 9 |
L1, мм |
19,5 |
| 10 |
L2, мм |
4,5+0,5 |
| 11 |
d, мм |
4-0,012 |
| 12 |
Средняя наработка до отказа, не менее, ч |
100 |
| 13 |
Средний срок службы двигателя, не менее, лет |
10 |
Электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40 применяется для привода кофемолок и других бытовых приборов.
1.3 Цель испытаний
Целью испытаний является определение фактических показателей надежности объекта исследования, таких как: среднее время безотказной работы T(средняя наработка до отказа), вероятность безотказной работы объекта в течение времени P(t), вероятность отказа Q(t), плотность распределения времени до отказа f(t), интенсивность отказа λ(t) в момент времениt.
1.4 Место проведения и обеспечение испытаний
Испытательный центр ОАО «ПЭМЗ», аккредитованный Федеральным агентством по техническому регулированию и метрологии для проведения испытаний с целью сертификации.
1.5 Объем и методика испытаний
Испытания проводятся по плану [NUN], согласно которому испытывают одновременно N=100
объектов, отказавшие во время испытаний объекты не восстанавливают и не заменяют, испытания прекращают, когда число отказавших объектов достигло N
=100.
1.6 Обработка результатов испытаний
1.6.1 Постановка задачи
Требуется определить показатели надежности объекта испытаний по опытным данным определительных испытаний.
На испытания поставлено N = 100 объектов. Моменты отказов объекта испытаний представлены в таблице 2. Все объекты работают до своего отказа и после отказа не ремонтируются. Требуется определить статистические и теоретические показатели надежности объекта: T
, P
(
t
),
Q
(
t
)
, f
(
t
)
, λ(
t
).
Таблица 2 –
Моменты отказов объектов, в часах
| 350 |
244 |
69 |
234 |
145 |
196 |
389 |
23 |
251 |
127 |
| 226 |
118 |
219 |
204 |
120 |
180 |
406 |
182 |
74 |
240 |
| 206 |
257 |
181 |
104 |
130 |
341 |
245 |
9 |
226 |
161 |
| 147 |
71 |
219 |
361 |
162 |
112 |
67 |
182 |
34 |
76 |
| 143 |
60 |
119 |
190 |
281 |
437 |
226 |
307 |
41 |
148 |
| 228 |
37 |
296 |
51 |
254 |
44 |
190 |
143 |
795 |
117 |
| 191 |
14 |
392 |
157 |
16 |
203 |
89 |
346 |
303 |
40 |
| 377 |
319 |
258 |
37 |
68 |
235 |
385 |
128 |
111 |
640 |
| 136 |
224 |
174 |
601 |
35 |
71 |
345 |
132 |
197 |
35 |
| 331 |
83 |
97 |
178 |
328 |
194 |
110 |
120 |
106 |
109 |
1.6.2 Вычисление основных характеристик выборки
Основными числовыми характеристиками выборочной совокупности является: выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое (или стандартное) отклонение, наименьшие и наибольшие значения, размах выборки, асимметрия, эксцесс.
Для расчета указанных характеристик в Excel необходимо поставить курсор в ячейку, в которую будет записано значение характеристики, вызвать соответствующую функцию и в качестве ее аргумента указать блок ячеек со статистическими данными.
Для удобства следующих операций значения случайной величины Z (статистические данные) перепишем на другой лист в прямоугольный блок ячеек, например А1:J10.
Значения вычисляемых характеристик будет располагаться в ячейках F12 по F19.
Таблица 3 – Расчет выборочных характеристик
| A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
| 1
|
99 |
91 |
104 |
114 |
97 |
91 |
99 |
101 |
99 |
95 |
| 2
|
109 |
98 |
119 |
84 |
102 |
120 |
107 |
97 |
110 |
102 |
| 3
|
88 |
99 |
99 |
104 |
103 |
110 |
96 |
85 |
109 |
89 |
| 4
|
79 |
100 |
111 |
103 |
89 |
92 |
109 |
99 |
91 |
86 |
| 5
|
100 |
90 |
102 |
91 |
89 |
95 |
98 |
87 |
117 |
100 |
| 6
|
95 |
98 |
97 |
107 |
90 |
112 |
85 |
101 |
94 |
87 |
| 7
|
99 |
93 |
104 |
90 |
90 |
109 |
89 |
95 |
102 |
88 |
| 8
|
100 |
98 |
93 |
104 |
107 |
98 |
104 |
112 |
100 |
105 |
| 9
|
115 |
113 |
94 |
110 |
93 |
94 |
82 |
100 |
94 |
102 |
| 10
|
90 |
94 |
102 |
110 |
90 |
99 |
93 |
87 |
115 |
97 |
| 11
|
| 12
|
Выборочное среднее |
98,68 |
| 13
|
Выборочная дисперсия |
76,86626 |
| 14
|
Выборочное ср. квадр. отклонение |
8,767341 |
| 15
|
Наименьшее значение |
79 |
| 16
|
Наибольшее значение |
120 |
| 17
|
Размах выборки |
41 |
| 18
|
Асимметрия |
0,282254 |
| 19
|
Эксцесс |
-0,38419 |
Вычисление выборочных характеристик осуществляется по формулам:
- выборочное среднее F12 = СРЗНАЧ (A1:J10);
- выборочная дисперсия F13 = ДИСП (A1:J10);
- выборочное среднее квадратическое отклонение
F14 = СТАНДОТКЛОН (A1:J10) или F14 = КОРЕНЬ (F13);
- Наименьшее значение: F15 = МИН(A1:J10);
- Наибольшее значение: F16 = МАКС(A1:J10);
- Размах выборки: F17 = F16-F15;
- Асимметрия: F18 = СКОС(A1:J10);
- Эксцесс: F19 = ЭКСЦЕСС(A1:J10).
1.6.3 Формирование статистического ряда и графическое представление данных
Для наглядного представления статистических данных воспользуемся группировкой. Числовая ось при этом разбивается на интервалы, и для каждого интервала подсчитывается число элементов выборки, которые в него попали. Группировка данных производится в следующей последовательности:
наименьшее значение округляется в меньшую сторону, а наибольшее – в большую сторону до «хороших» чисел хmin
и хmax
;
выбирается количество групп k, удовлетворяющее неравенству; иногда оно определяется по формуле k=[5lgn]. Если объем выборки n=100, то k=10;
находится шаг по формуле:
 , ,
где R = хmax
- хmin
– длина промежутка, в котором содержатся статистические данные;
определяются границы частичных интервалов:
а0
= х
min
, а1
= а0
+
h
,
a
2
=
a
1
+
h
, … ,
ak
=
ak
-1
+
h
= х
max
;
в каждом интервале вычисляются средние значения
 ; ;
для каждого интервала [ai
-1
,ai
], i = 1,2, …,k находятся:
– частоты ni
, т.е. число выборочных значений, попавших в интервал;
– относительные частоты  ; ;
– накопленные частоты wi
=
n
1
+
n
2
+ … +
ni
;
– накопленные относительные частоты  . .
Для выборочной совокупности (таблица 2) результаты группировки представим в таблице 4. Сначала укажем объем выборки, максимальное и минимальное значение, размах выборки, количество групп и шаг:
А22 = 100, В22 = 120, С22 = 70, D22 = B22 – C22, E22 = 10, F22 = D22/E22.
В ячейках А24:H24 укажем заголовки будущей таблицы. В этой таблице колонки В и С можно заполнить соответствующими формулами, представленными выше, для определения границ интервалов. Колонку D заполним по формуле: D30 = (B25+C25)/2, с последующим копированием в ячейки D26:D34.
Таблица 4 – Группировка статистических данных
| A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
| n
|
Xmax
|
Xmin
|
R
|
k
|
h
|
| 22
|
100 |
120 |
70 |
50 |
10 |
5 |
| 23
|
| 24
|
Группа |
Левая граница |
Правая граница |
Середина |
Частота |
Относ. частота |
Накоп. частота |
Накоп. относ. частота |
| 25
|
1 |
70 |
75 |
72,5 |
0 |
0 |
0 |
0 |
| 26
|
2 |
75 |
80 |
77,5 |
1 |
0,01 |
1 |
0,01 |
| 27
|
3 |
80 |
85 |
82,5 |
4 |
0,04 |
5 |
0,05 |
| 28
|
4 |
85 |
90 |
87,5 |
16 |
0,16 |
21 |
0,21 |
| 29
|
5 |
90 |
95 |
92,5 |
18 |
0,18 |
39 |
0,39 |
| 30
|
6 |
95 |
100 |
97,5 |
24 |
0,24 |
63 |
0,63 |
| 31
|
7 |
100 |
105 |
102,5 |
16 |
0,16 |
79 |
0,79 |
| 32
|
8 |
105 |
110 |
107,5 |
11 |
0,11 |
90 |
0,9 |
| 33
|
9 |
110 |
115 |
112,5 |
7 |
0,07 |
97 |
0,97 |
| 34
|
10 |
115 |
120 |
117,5 |
3 |
0,03 |
100 |
1 |
Для заполнения колонки Е выделим ячейки Е25:Е34 и воспользуемся функцией ЧАСТОТА, указав массив статистических данных и массив правых границ интервалов: { = ЧАСТОТА (А1:J10; C25:C34)}
Одновременным нажатием клавиш заполним остальные выделенные ячейки.
Колонку F заполним с помощью формулы:
F25 = E25/$A$22, с последующим копированием в ячейки F26:F34
Колонку G заполним с помощью формулы:
G25 = E25, G26 = G25 + E26, с последующим копированием в ячейки G32:G39
Колонку H заполним с помощью формулы:
H25 = G25/$A$22, с последующим копированием в ячейки H26:H34
Данные, собранные в таблице 4 наглядно представим с помощью:
полигон частот – графическая зависимость частот (относительных частот) от середины интервалов (рисунок 1).
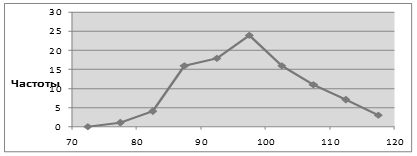
Рисунок 1 – Полигон частот
кумуляты частот – графическая зависимость накопленных частот (накопленных относительных частот) от середины интервалов (рисунок 2).
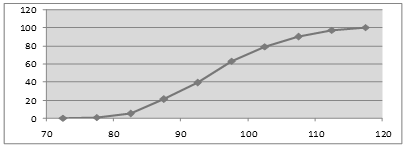
Рисунок 2 – Кумулята частот
1.6.4 Подбор подходящего закона распределения вероятностей
Далее рассмотрим некоторые известные распределения, такие как экспоненциальное, нормальное и гамма-распределение, с целью проверки подчиняется ли наше распределение вероятностей заданному.
Проверка на соответствие данных испытаний распределению производится перебором трех распределений, указанных выше, включая заданное, а именно гамма-распределение.
Чтобы иметь полную информацию о распределении случайной величины, надо знать параметры этого распределения. Таким образом, математическое ожидание случайной величины t равно выборочной средней, а среднее квадратическое отклонение случайной величины t – выборочному среднему квадратическому отклонению. Указанные характеристики находятся в ячейках F12 и F14 соответственно. Поместим эти значения в ячейки А2 и В2 соответственно (таблица 5).
Определим параметры экспоненциального (λ), нормального (m – математическое отклонение и σ – среднее квадратическое отклонение) и гамма-распределения (α и β) в соответствии с формулами:
 , ,  , , 
B5 = 1/A2;
B8 = A2;
B9 = B2;
B12 = (A2/B2)^2;
B13 = B2^2/A2.
Таблица 5 – Значения плотностей распределения
| A
|
B
|
C
|
D
|
E
|
| 1
|
Матем. ожидание |
Ср. кв. отклон. |
| 2
|
98,68 |
8,767340682 |
| 3
|
| 4
|
Параметры экспоненциального распределения |
| 5
|
λ |
0,0101 |
| 6
|
| 7
|
Параметры нормального распределения |
| 8
|
m
|
98,6800 |
| 9
|
σ |
8,767340682 |
| 10
|
| 11
|
Параметры гамма-распределения |
| 12
|
α |
126,6842 |
| 13
|
β |
0,7789 |
| 14
|
| 15
|
Середина |
Плотность относит. частот |
Плотность экспоненц. распред. |
Плотность нормал. распред. |
Плотность гамма- распред. |
| 16
|
72,5000 |
0 |
0,0049 |
0,0005 |
0,0003 |
| 17
|
77,5000 |
0,002 |
0,0046 |
0,0025 |
0,0019 |
| 18
|
82,5000 |
0,008 |
0,0044 |
0,0083 |
0,0080 |
| 19
|
87,5000 |
0,032 |
0,0042 |
0,0202 |
0,0213 |
| 20
|
92,5000 |
0,036 |
0,0040 |
0,0355 |
0,0374 |
| 21
|
97,5000 |
0,048 |
0,0038 |
0,0451 |
0,0456 |
| 22
|
102,5000 |
0,032 |
0,0036 |
0,0414 |
0,0399 |
| 23
|
107,5000 |
0,022 |
0,0034 |
0,0274 |
0,0259 |
| 24
|
112,5000 |
0,014 |
0,0032 |
0,0131 |
0,0128 |
| 25
|
117,5000 |
0,006 |
0,0031 |
0,0045 |
0,0049 |
В ячейках В16:В25 вычислим плотности относительных частот как частное от деления относительных частот (ячейки F25:F34) на шаг (ячейка $F$22) из таблицы 4.
Плотности экспоненциального, нормального и гамма-распределений рассчитываются в соответствии с формулами:
С16 = ЭКСПРАСП (А16;$B$5;ЛОЖЬ);
D16 = НОРМРАСП (А16;$B$8;$B$9;ЛОЖЬ);
E16 = ГАММАРАСП (А16;$B$12;$B$13;ЛОЖЬ).
Затем копируем их в блок ячеек С17:Е25.
После чего строим гистограмму частот, совмещенную с плотностью каждого из указанных ранее распределений. Графическое изображение гистограммы кривых различных распределений приведены на рисунках 3- 5.
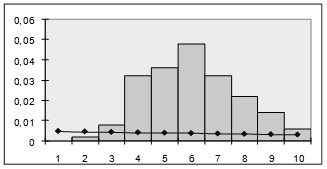
Рисунок 3 – Сглаживание гистограммы плотностью экспоненциального распределения
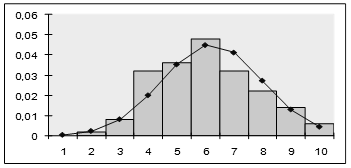
Рисунок 4 – Сглаживание гистограммы плотностью нормального распределения
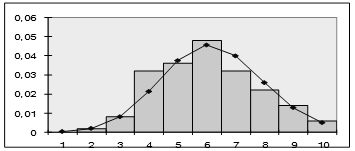
Рисунок 5 – Сглаживание гистограммы плотностью гамма-распределения
Используя критерий χ2
, установим, верна ли принятая гипотеза о том, что статистические данные подчиняются нормальному распределению.
Для применения критерия χ2
необходимо, чтобы частоты ni
, соответствующие каждому интервалу, были не меньше 5. Для этого при необходимости объединим рядом стоящие интервалы, а их частоты суммируем. Далее вычислим следующую сумму:
 , ,
где pi
– теоретическая вероятность того, что случайная величина Х примет значение из интервала [ai
-1
,ai
].
Предположим, что случайная величина t имеет функцию распределения F(t), поэтому pi
= F(ai
) – F(ai
-1
).
Образец расчетов по предыдущей формуле для трех распределений представлен в таблице 6.
В колонке А содержатся левые, а в колонке В – праве границы интервалов. В колонке С находятся соответствующие частоты. В колонке D рассчитываются теоретические вероятности в зависимости от вида распределения.
Для экспоненциального распределения:
D31 = ЭКСПРАСП (B31; $B$5; ИСТИНА) – ЭКСПРАСП (А31; $B$5; ИСТИНА);
Для нормального распределения:
D40 = НОРМРАСП (В40; $B$8; $B$9; ИСТИНА) – НОРМРАСП (А40; $B$8; $B$9; ИСТИНА);
Для гамма-распределения:
D49 = ГАММАРАСП (В49; $B$12; $B$13; ИСТИНА) – ГАММАРАСП (А49; $B$12; $B$13$ ИСТИНА).
В колонке Е рассчитываются слагаемые соотношения по формуле:
Е31 = (С31-100*В31)^2/(100*D31), которая копируется в другие ячейки колонки Е.
После чего для каждого рассмотренного распределения определим итоговые суммы:
Е38 = СУММ(E34:E39);
Е47 = СУММ(E42:E47);
Е56 = СУММ(Е50:Е55).
Которые равны соответственно 659,6862; 5,2199 и 3,8740.
Гипотеза о виде закона распределения должна быть принята, если вычисленное значение χ2
выч
достаточно мало, а именно не превосходит критического значения χ2
кр
, которое определяется по распределению χ2
в зависимости от заданного уровня значимости α и числа степеней свободы r=k’
– s – 1. где k’
– количество интервалов после объединения; s – число неизвестных параметров распределения, которые были определены по выборке.
В данном примере r = 7 – 2 – 1 = 2
Критическое значение рассчитывается по формуле:
Е57 = ХИ2ОБР(0,05;4), из таблицы 6 видно, оно равно 9,4877.
Поскольку 5,2199<9,4877, то принимается гипотеза о том, что статистические данные имеют нормальное распределение с параметрами α = = 98,68и σ = 8,7673 соответственно.
Таблица 6 – Подбор распределения на основе критерия χ2
| А
|
B
|
С
|
D
|
E
|
| 29
|
Левая граница |
Правая граница |
Частота |
Вероятности |
χ² |
| 30
|
Экспоненциальное распределение |
| 31
|
70 |
85 |
5 |
0,069374468 |
0,5411 |
| 32
|
85 |
90 |
16 |
0,020878363 |
92,7028 |
| 33
|
90 |
95 |
18 |
0,019846835 |
129,2349 |
| 34
|
95 |
100 |
24 |
0,018866271 |
259,1934 |
| 35
|
100 |
105 |
16 |
0,017934153 |
112,5378 |
| 36
|
105 |
110 |
11 |
0,017048088 |
50,6805 |
| 37
|
110 |
120 |
10 |
0,031610928 |
14,7957 |
| 38
|
Сумма |
659,6862 |
| 39
|
Нормальное распределение |
| 40
|
70 |
85 |
5 |
0,058804812 |
0,1318 |
| 41
|
85 |
90 |
16 |
0,101737571 |
3,3365 |
| 42
|
90 |
95 |
18 |
0,176260064 |
0,0079 |
| 43
|
95 |
100 |
24 |
0,222500256 |
0,1376 |
| 44
|
100 |
105 |
16 |
0,204663183 |
0,9747 |
| 45
|
105 |
110 |
11 |
0,137173828 |
0,5383 |
| 46
|
110 |
120 |
10 |
0,090811892 |
0,0930 |
| 47
|
Сумма |
5,2199 |
| 48
|
Гамма-распределение |
| 49
|
70 |
85 |
5 |
0,053672643 |
0,0251 |
| 50
|
85 |
90 |
16 |
0,107072418 |
2,6163 |
| 51
|
90 |
95 |
18 |
0,185399233 |
0,0157 |
| 52
|
95 |
100 |
24 |
0,224931406 |
0,1009 |
| 53
|
100 |
105 |
16 |
0,197757868 |
0,7209 |
| 54
|
105 |
110 |
11 |
0,129724735 |
0,2999 |
| 55
|
110 |
120 |
10 |
0,090713209 |
0,0951 |
| 56
|
Сумма |
3,8740 |
| 57
|
Критическое значение критерия |
9,4877 |
1.6.5 Определение характеристик надежности системы
После подтверждения гипотезы о виде закона распределения, определим характеристики надежности системы. Ббыло установлено, что случайная величина имеет плотность распределения вероятностей:

Основными характеристиками надежности невосстанавливаемой системы являются вероятность безотказной работы, и вероятность отказа в течение времени t
.
Данные характеристики вычисляются по формулам:
В64 = 1 - НОРМРАСП (А64; $B$8; $B$9; ИСТИНА);
С64 = 1 - В64;
Плотность распределения и интенсивность отказа рассчитаем по следующим формулам:
D64 = НОРМРАСП (А64; $B$8; $B$9; ЛОЖЬ);
E64 = D64/B64.
Далее скопируем формулы в ячейки В64:В74, С64:С74, D64:D74, E64:E74 соответственно.
В результате будет получена таблица вычисленных ранее значений (таблица 7) и построены их графики (рисунки 6,7,8).
Таблица 7 – Значения показателей надежности объекта испытаний
| А
|
B
|
C
|
D
|
E
|
| 63
|
t |
P(t) |
Q (t) |
f (t) |
λ (t) |
| 6
4
|
63,611 |
1,000 |
0,000 |
0,000 |
0,000 |
| 6
5
|
74,000 |
0,998 |
0,002 |
0,001 |
0,001 |
| 6
6
|
84,000 |
0,953 |
0,047 |
0,011 |
0,012 |
| 6
7
|
94,000 |
0,703 |
0,297 |
0,039 |
0,056 |
| 6
8
|
104,000 |
0,272 |
0,728 |
0,038 |
0,139 |
| 6
9
|
114,000 |
0,040 |
0,960 |
0,010 |
0,245 |
| 70
|
124,000 |
0,002 |
0,998 |
0,001 |
0,363 |
| 71
|
134,000 |
0,000 |
1,000 |
0,000 |
0,485 |

Рисунок 6 – График вероятности безотказной работы и вероятности отказа

Рисунок 7 – График плотности распределения вероятности

Рисунок 8 – График интенсивности отказа
1.6.6 Протокол испытаний
ИСПЫТАТЕЛЬНЫЙ ЦЕНТР
«ПЭМЗ-электро»
аттестат № РОСС RU.0004.13ЛРН02
ПРОТОКОЛ ИСПЫТАНИЙ № 13
ЗАКАЗЧИК:
ОАО «Старт», 445028, г. Тольятти, ул. Революционная 72а.
ПРОИЗВОДИТЕЛЬ ПРОДУКЦИИ:
ООО «Электротех», г. Самара, ул. Новосадовая 3.
ВИД ИСПЫТАНИЯ:
Определение фактических показателей надежности электродвигателя однофазного коллекторного переменного тока типа ДК 60 – 40.
ПРОДОЛЖИТЕЛЬНОСТЬ ИСПЫТАНИЙ:
10.09.2008 г. – 25. 12. 2008 г.
ДОГОВОР №:
По заявке от 01.09.2008 г.
ТЕКСТ:
2 стр.
ЦЕЛЬ ИСПЫТАНИЯ:
Определение реального уровня надежности у предъявляемых объектов по опытным данным определительных испытаний.
ОТБОР ОБРАЗЦОВ:
Дата отбора: 15.09.2008 г.
Место отбора: склад
Другие сведения: отбор образцов и их подготовка к испытаниям по ГОСТ Р 11828-86.
ХАРАКТЕРИСТИКА ОБРАЗЦОВ:
Вид продукции: электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40.
Другие сведения: средняя наработка до отказа не менее 90 ч.
МЕТОДИКА ИСПЫТАНИЙ:
Испытания проводились по плану [NUN], согласно которому испытывались одновременно 100 объектов, отказавшие во время испытаний объекты не подлежали восстановлению и не заменялись, испытания прекращались, когда число отказавших объектов достигло также 100.
РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
Значения показателей надежности объекта испытаний приведены в таблице.
| t |
P(t) |
Q (t) |
f (t) |
λ (t) |
| 63,611 |
1,000 |
0,000 |
0,000 |
0,000 |
| 74,000 |
0,998 |
0,002 |
0,001 |
0,001 |
| 84,000 |
0,953 |
0,047 |
0,011 |
0,012 |
| 94,000 |
0,703 |
0,297 |
0,039 |
0,056 |
| 104,000 |
0,272 |
0,728 |
0,038 |
0,139 |
| 114,000 |
0,040 |
0,960 |
0,010 |
0,245 |
| 124,000 |
0,002 |
0,998 |
0,001 |
0,363 |
| 134,000 |
0,000 |
1,000 |
0,000 |
0,485 |
Заключение:
Результаты испытаний: электродвигатели соответствуют требованиям по средней продолжительности горения.
Руководитель ИЦ «ПЭМЗ-электро» Д.В. Айдаров
Руководитель группы испытаний ИЦ «ПЭМЗ-электро» А. А. Телепова
2. Пример обработки результатов испытаний для невосстанавливаемого объекта испытаний
Постановка задачи
На испытаниях находится N
= 56 объектов с восстановлением. В течение периода Т
= 600 часов регистрируются моменты времени отказов элементов (таблица 8). Предполагается, что отказавшие элементы заменяют идентичными по надежности элементами. Требуется определить показатели надежности элемента, характеризующие время его работы между соседними отказами: Т,
P
(
t
),
Q
(
t
)
, f
(
t
), λ(
t
).
Испытания проводятся по плану [NRT], согласно которому одновременно начинают испытания N=56 объектов, отказавшие во время испытаний объекты заменяют новыми, испытания прекращают при истечении времени испытаний или наработки T.
Обработка статистических данных предусматривает их группировку в 10 частичных интервалах (классах). Уровень значимости принять равным 0,05.
Таблица 8 – Время между отказами элементов
| Номер элемента |
Моменты отказа на периоде времени 600 часов |
| 1 |
104; 93; 107; 118; 89; 86 |
| 2 |
86; 98; 116; 82; 110; 103 |
| 3 |
106; 112; 94; 83; 98; 91 |
| 4 |
94; 106; 102; 107; 89; 91 |
| 5 |
117; 96; 103; 117; 83 |
| 6 |
94; 92; 107; 108; 106 |
| 7 |
90; 96; 84; 107; 99; 99 |
| 8 |
104; 106; 99; 103; 94; 82 |
| 9 |
99;95; 106; 119; 111 |
| 10 |
109; 118; 104; 95; 98 |
2.2 Вычисление основных характеристик выборки
Основными числовыми характеристиками выборочной совокупности являются: выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое (или стандартное) отклонение, наименьшее и наибольшее значения, размах выборки, асимметрия, эксцесс.
Значения вычисляемых характеристик расположим в ячейках с F12 по F19, как показано в таблице 9.
Таблица 9 – Расчет выборочных характеристик
| A
|
B
|
C
|
D
|
E
|
F
|
| 1
|
104 |
93 |
107 |
118 |
89 |
86 |
| 2
|
86 |
98 |
116 |
82 |
110 |
103 |
| 3
|
106 |
112 |
94 |
83 |
98 |
91 |
| 4
|
94 |
106 |
102 |
107 |
89 |
91 |
| 5
|
117 |
96 |
103 |
117 |
83 |
| 6
|
94 |
92 |
107 |
108 |
106 |
| 7
|
90 |
96 |
84 |
107 |
99 |
99 |
| 8
|
104 |
106 |
99 |
103 |
94 |
82 |
| 9
|
99 |
95 |
106 |
119 |
111 |
| 10
|
109 |
118 |
104 |
95 |
98 |
| 11
|
| 12
|
Выборочное среднее |
100,0892857 |
| 13
|
Выборочная дисперсия |
100,7373377 |
| 14
|
Выборочное ср. квадр. отклонение |
10,03679917 |
| 15
|
Наименьшее значение |
82 |
| 16
|
Наибольшее значение |
119 |
| 17
|
Размах выборки |
37 |
| 18
|
Асимметрия |
0,012585618 |
| 19
|
Эксцесс |
-0,711512555 |
Вычислим числовые характеристики выборочной совокупности по формулам:
Выборочное среднее: F12 = CРЗНАЧ(A1:F10);
Выборочная дисперсия: F13 = ДИСП(A1:F10);
Выборочное среднее квадратическое отклонение:
F14 = СТАНДОТКЛОН(A1:F10);
Наименьшее значение: F15 = МИН(A1:F10);
Наибольшее значение: F16 = МАКС(A1:F10);
Размах выборки: F17 = F16-F15;
Асимметрия: F18 = СКОС(A1:F10);
Эксцесс: F19 = ЭКСЦЕСС(A1:F10).
2.3 Формирование статистического ряда и графическое представление данных
Для наглядного представления статистических данных воспользуемся группировкой. Группировка данных производится в той же последовательности, что и в пункте 1.6.2 данной работы.
Для выборочной совокупности (таблица 8) результаты группировки представим в таблице 10. Сначала укажем объем выборки, максимальное и минимальное значение, размах выборки, количество групп и шаг:
А22 = 56, В22 =120, С22 = 80, D22 = B22 – C22, E22 =10, F22 = D22/E22
В этой таблице колонки В и С заполним левыми и правыми границами соответственно. Колонку D заполним по формуле:
D25 = (B25+C25)/2, с последующим копированием в ячейки D26:D34.
Таблица 10 – Группировка статистических данных
| A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
| 2
1
|
n
|
Xmax
|
Xmin
|
R
|
k
|
h
|
| 2
2
|
56 |
120 |
80 |
40 |
10 |
4 |
| 2
3
|
| 2
4
|
Группа |
Левая граница |
Правая граница |
Середина |
Частота |
Относ. частота |
Накоп. частота |
Накоп. относ. частота |
| 2
5
|
1 |
80 |
84 |
82 |
5 |
0,0892 |
5 |
0,0892 |
| 2
6
|
2 |
84 |
88 |
86 |
2 |
0,0357 |
7 |
0,125 |
| 27
|
3 |
88 |
92 |
90 |
6 |
0,1071 |
13 |
0,2321 |
| 28
|
4 |
92 |
96 |
94 |
9 |
0,1607 |
22 |
0,3928 |
| 29
|
5 |
96 |
100 |
98 |
7 |
0,125 |
29 |
0,5178 |
| 30
|
6 |
100 |
104 |
102 |
7 |
0,125 |
36 |
0,6428 |
| 31
|
7 |
104 |
108 |
106 |
10 |
0,1785 |
46 |
0,8214 |
| 32
|
8 |
108 |
112 |
110 |
4 |
0,0714 |
50 |
0,8928 |
| 33
|
9 |
112 |
116 |
114 |
1 |
0,0178 |
51 |
0,9107 |
| 34
|
10 |
116 |
120 |
118 |
5 |
0,0892 |
56 |
1 |
Для заполнения колонки Е выделим ячейки Е25:Е34 и воспользуемся функцией ЧАСТОТА, указав массив статистических данных и массив правых границ интервалов: { = ЧАСТОТА (А1:F10; C25:C34)}
Одновременным нажатием клавиш заполним остальные выделенные ячейки.
Колонку F заполним с помощью формулы:
F25 = E25/$A$22, с последующим копированием в ячейки F26:F34
Колонку G заполним с помощью формулы:
G25 = E25, G26 = G25 + E26 с последующим копированием в ячейки G27:G34
Колонку H заполним с помощью формулы:
H25 = G25/$A$22, с последующим копированием в ячейки H26:H34
Данные, собранные в таблице 10 наглядно представим с помощью:
полигон частот – графическая зависимость частот (относительных частот) от середины интервалов (рисунок 9).
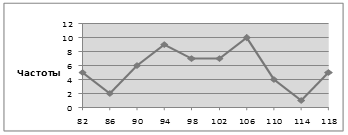
Рисунок 9 – Полигон частот
кумуляты частот – графическая зависимость накопленных частот (накопленных относительных частот) от середины интервалов (рисунок 10).
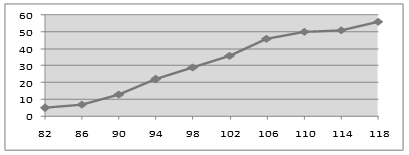
Рисунок 10 – Кумуляты частот
2.4 Подбор подходящего закона распределения вероятностей
Далее рассмотрим некоторые известные распределения, такие как равномерное, нормальное и гамма-распределение, с целью проверки подчиняется ли наше распределение вероятностей заданному.
Проверка на соответствие данных испытаний распределению производится перебором трех распределений, указанных выше, включая заданное, а именно равномерное.
Чтобы иметь полную информацию о распределении случайной величины, надо знать параметры этого распределения. Таким образом, математическое ожидание случайной величины t равно выборочной средней, а среднее квадратическое отклонение случайной величины t – выборочному среднему квадратическому отклонению. Указанные характеристики находятся в ячейках F12 и F14 соответственно. Поместим эти значения в ячейки А2 и В2 соответственно (таблица 11).
Определим параметры равномерного (a и b), нормального (m – математическое отклонение и σ – среднее квадратическое отклонение), экспоненциального и гамма-распределения (α и β) в соответствии с формулами:
 , ,  , ,  , ,  , , 
B5 = 1/A2;
B8 = A2-В2*КОРЕНЬ(3);
B9 = А2+В2*КОРЕНЬ(3);
B12 = (A2/B2)^2;
B13 = B2^2/A2;
B16 = (A2/B2)^2;
B17 = B2^2/A2.
Таблица 11 – Значения плотностей распределения
| A
|
B
|
C
|
D
|
E
|
F
|
| 1
|
Матем. ожидание |
Ср. кв. отклон. |
| 2
|
100,0892 |
10,0367 |
| 3
|
| 4
|
Параметры экспоненциального распределения |
| 5
|
λ |
0,0100 |
| 6
|
| 7
|
Параметры равномерного распределения |
| 8
|
а
|
82,7050 |
| 9
|
b
|
117,4735 |
| 10
|
| 11
|
Параметры нормального распределения |
| 12
|
m
|
100,0893 |
| 13
|
σ |
10,0367 |
| 14
|
| 15
|
Параметры гамма-распределения |
| 16
|
α |
99,4454 |
| 17
|
β |
1,0065 |
| 18
|
| 19
|
Середина |
Плотность относит. частот |
Плотность экспоненц. распред. |
Плотность нормал. распред. |
Плотность гамма- распред. |
Плотность равномер. распред. |
| 20
|
82 |
0,0223 |
0,0044 |
0,0078 |
0,0076 |
0 |
| 21
|
86 |
0,0089 |
0,0042 |
0,0148 |
0,0156 |
0,0287 |
| 22
|
90 |
0,0267 |
0,0041 |
0,0240 |
0,0257 |
0,0287 |
| 23
|
94 |
0,0401 |
0,0039 |
0,0331 |
0,0349 |
0,0287 |
| 24
|
98 |
0,0312 |
0,0038 |
0,0389 |
0,0397 |
0,0287 |
| 25
|
102 |
0,0312 |
0,0036 |
0,0390 |
0,0383 |
0,0287 |
| 26
|
106 |
0,0446 |
0,0035 |
0,0334 |
0,0317 |
0,0287 |
| 27
|
110 |
0,0178 |
0,0033 |
0,0244 |
0,0229 |
0,0287 |
| 28
|
114 |
0,0044 |
0,0032 |
0,0152 |
0,0145 |
0,0287 |
| 29
|
118 |
0,0223 |
0,0031 |
0,0081 |
0,0081 |
0 |
В ячейках В20:В29 вычислим плотности относительных частот как частное от деления относительных частот (ячейки F25:F34) на шаг (ячейка $F$22) из таблицы 10.
Плотности равномерного, нормального, экспоненциального и гамма-распределений рассчитываются в соответствии с формулами:
С20 = ЭКСПРАСП (А20;$B$5;ЛОЖЬ);
D20 = НОРМРАСП (А20; $B$12; $B$13; ЛОЖЬ);
E20 = ГАММАРАСП (А20; $B$16; $B$17; ЛОЖЬ).
F20 = ЕСЛИ(А20<$B$8; 0; ЕСЛИ(A20>=$B$9; 1/($B$9-$B$8); 0));
Затем копируем их в блок ячеек С21:F21.
После чего строим гистограмму частот, совмещенную с плотностью каждого из указанных ранее распределений. Графическое изображение гистограммы кривых различных распределений приведены на рисунках 11- 13.
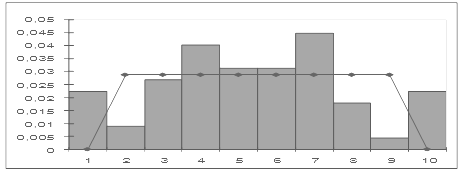
Рисунок 11 – Сглаживание гистограммы плотностью равномерного распределения
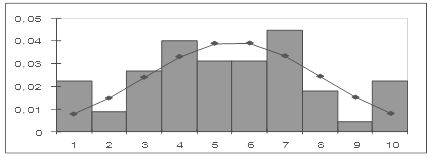
Рисунок 12 – Сглаживание гистограммы плотностью нормального распределения

Рисунок 13 – Сглаживание гистограммы плотностью гамма-распределения

Рисунок 14 – Сглаживание гистограммы плотностью экспоненциального распределения
Используя критерий χ2
, установим, верна ли принятая гипотеза о том, что статистические данные подчиняются равномерному распределению, так, чтобы ошибка не превышала заданного уровня значимости α (вероятность того, что будет отвергнута правильная гипотеза).
Для применения критерия χ2
необходимо, чтобы частоты ni
, соответствующие каждому интервалу, были не меньше 5. Для этого при необходимости объединим рядом стоящие интервалы, а их частоты суммируем. Далее вычислим следующую сумму:
 , ,
где pi
– теоретическая вероятность того, что случайная величина Х примет значение из интервала [ai
-1
,ai
].
Предположим, что случайная величина t имеет функцию распределения F(t), поэтому pi
= F(ai
) – F(ai
-1
).
Образец расчетов по предыдущей формуле для трех распределений представлен в таблице 6.
В колонке А содержатся левые, а в колонке В – праве границы интервалов. В колонке С находятся соответствующие частоты. В колонке D рассчитываются теоретические вероятности в зависимости от вида распределения.
Для экспоненциального распределения:
D35 = ЭКСПРАСП (B35; $B$5; ИСТИНА) – ЭКСПРАСП (А35; $B$5; ИСТИНА);
Для равномерного распределения:
D65 = ЕСЛИ (B65<$B$8; 0; ЕСЛИ (B65<=$B$9; (B24-$B$8) / ($B$6-$B$9); 1)) – ЕСЛИ (A24<$B$8; 0; ЕСЛИ (A24<=$B$9; (A24-$B$8) / ($B$6-$B$9); 1));
Для нормального распределения:
D45 = НОРМРАСП (В45; $B$12; $B$13; ИСТИНА) – НОРМРАСП (А45; $B$12; $B$13; ИСТИНА);
Для гамма-распределения:
D55 = ГАММАРАСП (В55; $B$16; $B$17; ИСТИНА) – ГАММАРАСП (А55; $B$16; $B$17; ИСТИНА).
В колонке Е рассчитываются слагаемые соотношения по формуле:
Е35 = (С35-56*D35)^2/(56*D35), которая копируется в другие ячейки колонки Е.
После чего для каждого рассмотренного распределения определим итоговые суммы:
Е43 = СУММ(E35:E42);
Е53 = СУММ(E45:E52);
Е63 = СУММ(Е55:Е62);
Е73 = СУММ(Е65:Е72).
Которые равны соответственно 349,8344; 14,8995; 15,1459; 16,7324.
Гипотеза о виде закона распределения должна быть принята, если вычисленное значение χ2
выч
достаточно мало, а именно не превосходит критического значения χ2
кр
, которое определяется по распределению χ2
в зависимости от заданного уровня значимости α и числа степеней свободы r=k’
– s – 1.
где k’
– количество интервалов после объединения;
s – число неизвестных параметров распределения, которые были определены по выборке.
В данном примере r = 7 – 2 – 1 = 5
Критическое значение рассчитывается по формуле:
Е74 = ХИ2ОБР(0,05;5), из таблицы 12 видно, оно равно 16,7496.
Поскольку 16,7324<16,7496, то принимается гипотеза о том, что статистические данные имеют равномерное распределение с параметрами a = 82,7050 и b = 117,4735 соответственно.
Таблица 12 – Подбор распределения на основе критерия χ2
| А
|
B
|
С
|
D
|
E
|
| 33
|
Левая граница |
Правая граница |
Частота |
Вероятности |
χ² |
| 34
|
Экспоненциальное распределение |
| 35
|
80 |
84 |
5 |
0,0176 |
16,3293 |
| 36
|
84 |
92 |
8 |
0,0331 |
20,2945 |
| 37
|
92 |
96 |
9 |
0,01562 |
75,4446 |
| 38
|
96 |
100 |
7 |
0,01501 |
45,1229 |
| 39
|
100 |
104 |
7 |
0,01442 |
47,4663 |
| 40
|
104 |
108 |
10 |
0,01385 |
109,6166 |
| 41
|
108 |
116 |
5 |
0,02611 |
8,5589 |
| 42
|
116 |
120 |
5 |
0,01229 |
27,0014 |
| 43
|
Сумма |
349,8344 |
| 45
|
Нормальное распределение |
| 46
|
80 |
84 |
5 |
0,0317 |
5,8201 |
| 47
|
84 |
92 |
8 |
0,1556 |
0,0590 |
| 48
|
92 |
96 |
9 |
0,1317 |
0,3576 |
| 49
|
96 |
100 |
7 |
0,1546 |
0,3175 |
| 50
|
100 |
104 |
7 |
0,1551 |
0,3280 |
| 51
|
104 |
108 |
10 |
0,1331 |
0,8698 |
| 52
|
108 |
116 |
5 |
0,1588 |
1,7057 |
| 53
|
116 |
120 |
5 |
0,03281 |
5,4419 |
| 54
|
Сумма |
14,8995 |
| 55
|
Гамма-распределение |
| 56
|
80 |
84 |
5 |
0,0310 |
6,1243 |
| 57
|
84 |
92 |
8 |
0,1652 |
0,1697 |
| 58
|
92 |
96 |
9 |
0,1388 |
0,1927 |
| 59
|
96 |
100 |
7 |
0,1576 |
0,3788 |
| 60
|
100 |
104 |
7 |
0,1522 |
0,2729 |
| 61
|
104 |
108 |
10 |
0,1265 |
1,1969 |
| 62
|
108 |
116 |
5 |
0,1497 |
1,3685 |
| 63
|
116 |
120 |
5 |
0,03281 |
5,4421 |
| 64
|
Сумма |
15,1459 |
| 65
|
Равномерное распределение |
| 66
|
80 |
84 |
5 |
0,03727 |
4,0719 |
| 67
|
84 |
92 |
8 |
0,2300 |
1,8522 |
| 68
|
92 |
96 |
9 |
0,1150 |
1,0151 |
| 69
|
96 |
100 |
7 |
0,1150 |
0,0482 |
| 70
|
100 |
104 |
7 |
0,1150 |
0,0482 |
| 71
|
104 |
108 |
10 |
0,1150 |
1,9643 |
| 72
|
108 |
116 |
5 |
0,2300 |
4,8254 |
| 73
|
116 |
120 |
5 |
0,0423 |
2,9070 |
| 74
|
Сумма |
16,7324 |
| 75
|
Критическое значение критерия |
16,74960237 |
2.5 Определение показателей надежности объекта испытаний
После подтверждения гипотезы о виде закона распределения, определим показатели надежности объекта.
Таким образом, было установлено, что случайная величина принадлежит множеству с плотностью распределения вероятностей:

Найдем основными показатели надежности. Они вычисляются по формулам:
В78 = ($B$6-А50)/($B$6-$B$5);
С78 = 1 – В78;
Плотность распределения и интенсивность отказа рассчитаем по следующим формулам:
D78 = 1/($B$9-$B$8);
E78 = D78/B78.
Далее скопируем формулы в ячейки В79:В84, С79:С84, D79:D84, E79:E84 соответственно.
В результате будет получена таблица вычисленных ранее значений (таблица 13) и построены их графики (рисунки 14,15,16).
Таблица 13 – Значения показателей надежности объекта испытаний
| А
|
B
|
C
|
D
|
E
|
| 78
|
82,7050 |
1 |
0 |
0,028761673 |
0,028761673 |
| 79
|
88 |
0,847708081 |
0,152291919 |
0,028761673 |
0,033928747 |
| 80
|
93 |
0,703899717 |
0,296100283 |
0,028761673 |
0,040860469 |
| 81
|
98 |
0,560091352 |
0,439908648 |
0,028761673 |
0,051351753 |
| 82
|
103 |
0,416282988 |
0,583717012 |
0,028761673 |
0,069091636 |
| 83
|
108 |
0,272474623 |
0,727525377 |
0,028761673 |
0,105557253 |
| 84
|
113 |
0,128666259 |
0,871333741 |
0,028761673 |
0,223537026 |
| 85
|

Рисунок 14 – График вероятности безотказной работы и вероятности отказа

Рисунок 15 – График плотности распределения вероятности
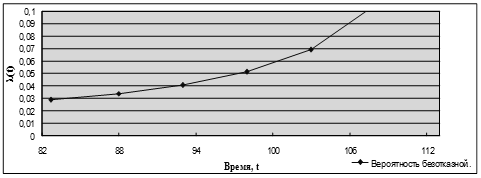
Рисунок 16 – График интенсивности отказа
Заключение
Поставленные перед нами цели курсовой работы по определению фактических показателей надежности невосстанавливаемого объекта испытания – электродвигателя однофазного коллекторного переменного тока типа ДК 60 – 40 – выполнены.
|