МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ХТУРЭ
Кафедра ОРТ
РАСЧЕТНО – ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОЙ РАБОТЕ
по курсу "Основы теории цепей"
Тема: Расчет характеристик и переходных процессов в электрических цепях
Выполнил:
студент группы ВEЗ-09-3
Моисеев В.П.
Проверил:
Долбин А.А.
Харьков 2009
СОДЕРЖАНИЕ
Задание
Введение
1. Определение характеристического сопротивления Z(w)
2. Определение классическим методом переходной характеристики  и построение ее графика и построение ее графика
3. Нахождение импульсной характеристики цепи  с использованием ее связи с с использованием ее связи с  , построение графика , построение графика 
4. Определение комплексного коэффициента передачи цепи 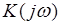 , построение графиков АЧХ и ФЧХ , построение графиков АЧХ и ФЧХ
5. Нахождение передаточной функции цепи 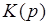 и установление ее связей с и установление ее связей с  и и 
6. Расчет отклика цепи на произвольное, построение графика отклика
Заключение
Список использованных источников
Приложение А
ЗАДАНИЕ
Схема и параметры цепи:
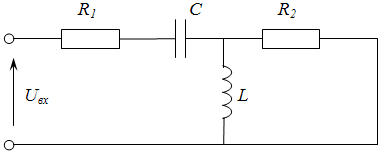
R1
=2 Ом; R2
= 800 Ом;
L = 2,3 мкГн;
C = 338 пФ.
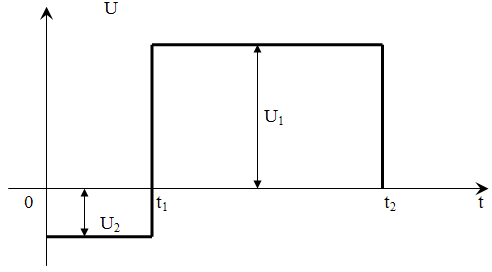
Параметры воздействия в виде импульса, показанного на рисунке ниже:
U1
= -16B; U2
=48B.
t1
= 14мкс; t2
= 28мкс.
Временная диаграмма импульсного воздействия  : :
ВВЕДЕНИЕ
Основная цель данной работы – закрепление и углубление знаний по разделам курса и формирование практических навыков применения методов анализа теории цепей, имеющих большое значение для изучения последующих дисциплин и для специальности радиоинженера в целом. Значение комплексного коэффициента передачи цепи, временных характеристик линейных цепей и методов анализа переходных процессов в линейных цепях, необходимо для изучения основных методов расчета радиотехнических устройств (спектрального, временного и операторного). Овладение этими методами позволяет выбирать в каждом конкретном случае наиболее рациональный, вытекающий из принципа работы устройства метод, а решение одной и той же задачи различными методами предохраняет от ошибок.
1. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО СОПРОТИВЛЕНИЯ Z(w)
Для определения характеристического сопротивления нужно составить уравнение:
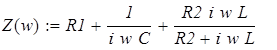
Приобразуем его:
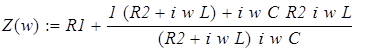 , ,

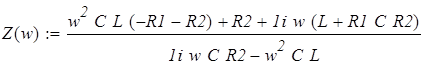 . .
Найдём модуль характеристического сопротивления ôZ(w)ô:
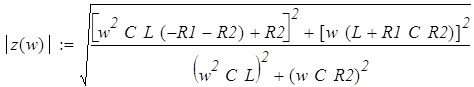 . .
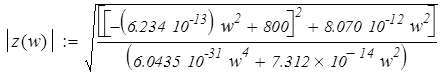
Подставив числовые значения, получим:
График зависимости модуля характеристического сопротивления от частоты показан на рисунке 1.1. Результаты расчетов представлены в дополнении А.
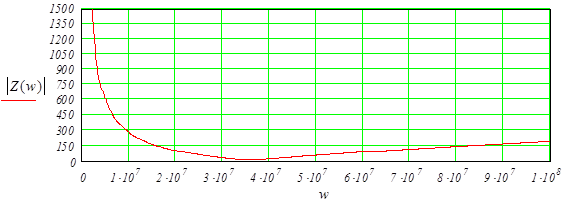
Рисунок 1.1 – График зависимости модуля характеристического сопротивления от частоты
Рассмотрим поближе тот промежуток зависимости модуля характеристического сопротивления от частоты, где он приближается к минимуму (рисунок 1.2).

Рисунок 1.2 – График зависимости модуля характеристического сопротивления от частоты (точка минимума)
Как видно из результатов расчетов, представленных в дополнении А, минимальное значение модуля характеристического сопротивления находится на частоте 3,58 ×107
рад/с.
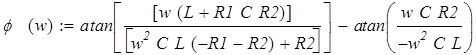
Найдём фазочастотную характеристику. Она равняется arctg от соотношения нериальной части к реальной характеристического сопротивления:
Подставив числовые значения, получим:
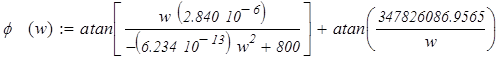
График ФЧХ представлен на рисунке 1.3.
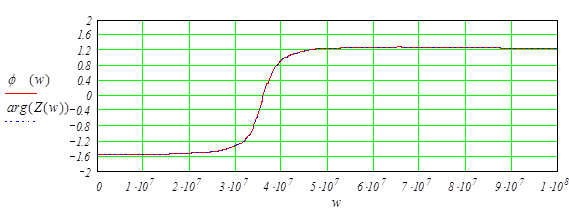
Рисунок 1.3 – График фазо - частотной характеристики
2. ОПРЕДЕЛЕНИЕ КЛАССИЧЕСКИМ МЕТОДОМ ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ  , ПОСТРОЕНИЕ ГРАФИКА , ПОСТРОЕНИЕ ГРАФИКА 
Поскольку схема содержит два накопительных элемента (C и L) в различных ветвях, данная цепь является цепью второго порядка. В ней возможны либо апериодический, либо колебательный режим. Для выяснения этого составим характеристическое уравнение и определим его корни.
Для определения корней характеристического уравнения можно воспользоваться следующей методикой – записать входное сопротивление в операторной форме 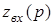 и приравнять его к нулю. В данной задаче получаем: и приравнять его к нулю. В данной задаче получаем:
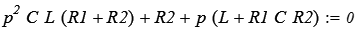 (1.1) (1.1)
откуда, находим корни этого уравнения.
Поскольку они комплексные, то:
 (1.2) (1.2)
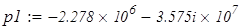
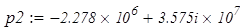
Цепь имеет колебательный характер, поэтому свободную составляющую решения можно определять в виде затухающего колебания:
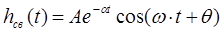 , (1.3) , (1.3)
где  и q - постоянные интегрирования. и q - постоянные интегрирования.
В данном случае  , так как ток в принужденном режиме через ёмкость С не пойдёт. , так как ток в принужденном режиме через ёмкость С не пойдёт.
Итак,
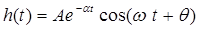
Чтобы определить постоянные интегрирования нужно составить два уравнения для начальных значений  и и  . .
Начальное значение 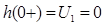 , т.к. по закону коммутации ток в начальный момент времени через индуктивность L равен току до включения. , т.к. по закону коммутации ток в начальный момент времени через индуктивность L равен току до включения.
Для нахождения произвольной переходной характеристики продифференцируем по времени по времени 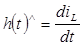 . .
Из курса ОРЭ известно, что напряжение на ёмкости равно:
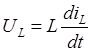 , откуда , откуда 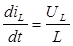 , ,
 , , 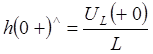 , ,
 . .
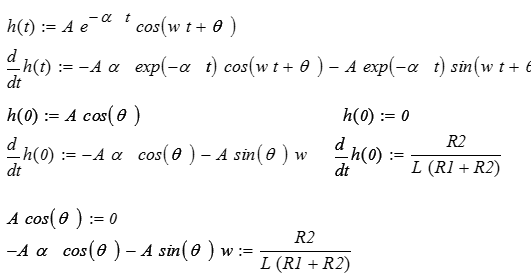
Учтя всё это можно составить систему уравнений:
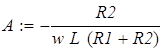 
Решение системы уравнений и подстановка данных приводит к значению:
Переходная характеристика после подстановки значений имеет вид:
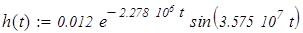
или
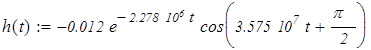
Её график изображен на рисунке 2.3. Расчетные данные находятся в приложении А.
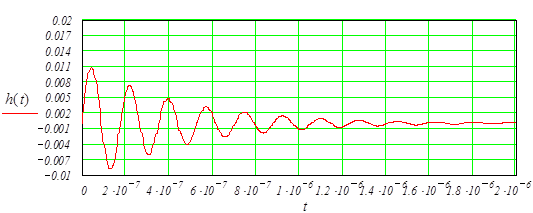
Рисунок 2.3 – График зависимости переходной характеристики 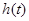
3. НАХОЖДЕНИЕ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ ЦЕПИ  С ИСПОЛЬЗОВАНИЕМ ЕЕ СВЯЗИ С С ИСПОЛЬЗОВАНИЕМ ЕЕ СВЯЗИ С  , ПОСТРОЕНИЕ ГРАФИКА , ПОСТРОЕНИЕ ГРАФИКА 
Импульсная характеристика вычисляется с помощью зависимости от  по формуле: по формуле:
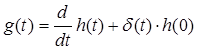 (3.1) (3.1)
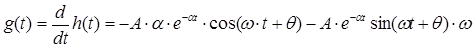 (3.2) (3.2)
В импульсной характеристике отсутствует дельта функция, поскольку  . .
После подстановки значений:
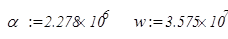
получим
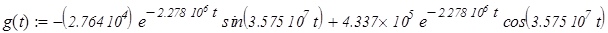
График импульсной функции изображен на рисунке 3.1. Расчетные данные находятся в приложении А.
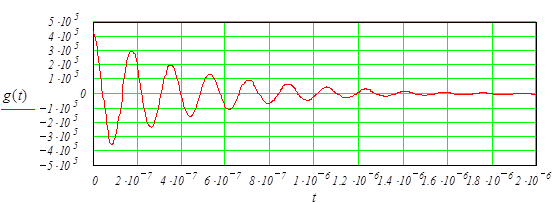
Рис.3.1 – График зависимости импульсной функции 
4. ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ЦЕПИ 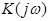 , ПОСТРОЕНИЕ ГРАФИКОВ АЧХ И ФЧХ , ПОСТРОЕНИЕ ГРАФИКОВ АЧХ И ФЧХ
Комплексный коэффициент передачи может быть представлен в показательной форме записи:
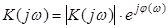 , (4.1) , (4.1)
где  - модуль комплексного коэффициента передачи; - модуль комплексного коэффициента передачи;
 - аргумент комплексного коэффициента передачи. - аргумент комплексного коэффициента передачи.
Модель комплексного коэффициента передачи представляет собой АЧХ цепи, а аргумент - ФЧХ цепи. Его можно найти из соотношения:

Напряжение на резисторе R2 равно напряжению на индуктивности L.
Выходя из этого, можно записать:

Комплексный коэффициент передачи при этом:
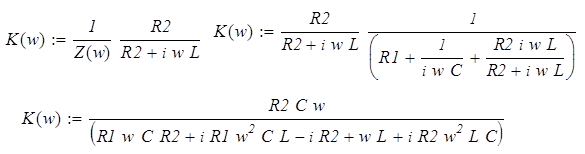
Выделим мнимую часть числа и найдём модуль (АЧХ):

Подставим значения в выведенные формулы и получим:
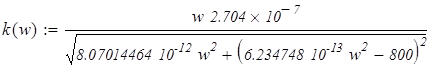
Аргумент комплексного коэффициента передачи (аргумент - ФЧХ цепи): комплексного коэффициента передачи (аргумент - ФЧХ цепи):
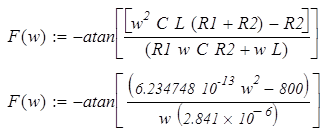
Г
рафики АЧХ , ФЧХ представлены на рисунках 4.1и 4.2 соответственно
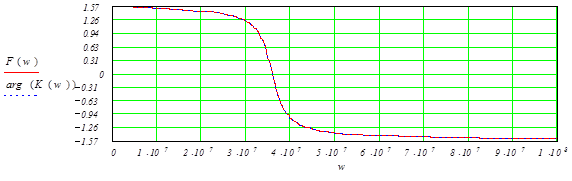
Рисунок 4.1 -АЧХ
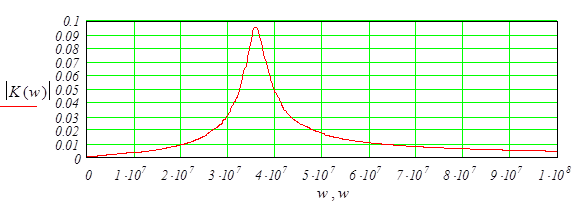
Рисунок 4.2 – ФЧХ
5. НАХОЖДЕНИЕПЕРЕДАТОЧНОЙ ФУНКЦИИ 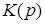 И УСТАНОВЛЕНИЕ ЕЕ СВЯЗИ С И УСТАНОВЛЕНИЕ ЕЕ СВЯЗИ С  И И 
Формально выражения для комплексного коэффициента передачи  и передаточной функцией и передаточной функцией  отличаются только переменной отличаются только переменной  для для и и для для 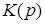 . .

Произведём замену:

Подставив значение

получим:
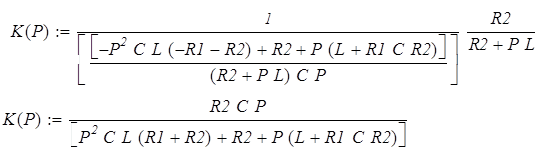
Умножим и поделим, прибавим и отнимем комплексно сопряженные числа:
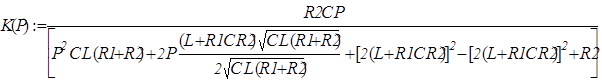
Сведём по формуле квадратов:
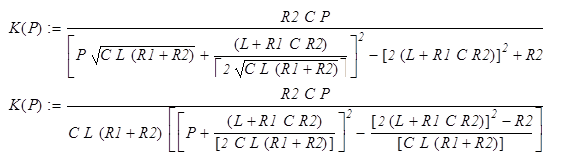
Подставив числовые значения и сделав еще некоторые преобразования получим:

Зная, что

запишем импульсную характеристику:
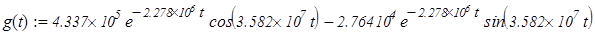
Зная, что

получим переходную характеристику:
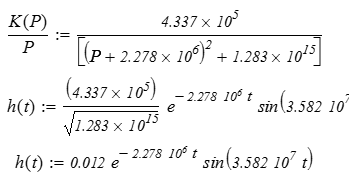
Полученные выражения для  и и совпадают с определенными в п.2 и п.3. совпадают с определенными в п.2 и п.3.
6. РАСЧЕТ ОТКЛИКА ЦЕПИ НА ПРОИЗВОЛЬНОЕ, ПОСТРОЕНИЕ ГРАФИКА ОТКЛИКА
Опишем входной сигнал (напряжение) с помощью простой функции:

Учитывая то, что вид реакции цепи - iL
запишем на каждом временном интервале функцию тока через напряжение:
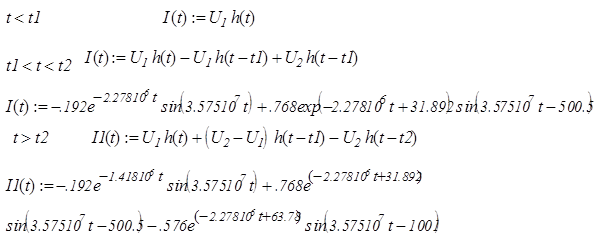
ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы были изучены классический и операторный методы нахождения временных характеристик. Классический метод оказался более прост, так как требовал меньше математических выкладок, для определения  и и  . Временные характеристики, найденные этими двумя методами совпали. Был применен комплексный метод для нахождения частотных характеристик цепи. . Временные характеристики, найденные этими двумя методами совпали. Был применен комплексный метод для нахождения частотных характеристик цепи.
Также были приобретены практические навыки применения интегралов наложения для расчета переходных процессов и прохождения простейших сигналов через цепи.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Основы теории цепей: Методические указания к курсовой работе для студентов – заочников специальности 23.01 "Радиотехника"/ Сост. Коваль Ю.А., Праги О.В. – Харьков: ХИРЭ, 1991. – 63 с.
2. Зернов Н.В., Карпов В.Г. "Теория электрических цепей". Издание 2-е, перераб. и доп., Л.,"Энергия",1987.
Приложение А
Результаты расчетов частотных характеристик

|