Національний технічний університет України
"Київський політехнічний інститут"
Курсова робота
з курсу: "Електронні системи керування та регулювання"
на тему: "Розрахунок трьохфазного мостового випрямляча"
Київ 2008
Зміст
Вступ
1.Теоретичні відомості про роботу пристрою
1.1 Силова частина. Трифазна вентильна схема (схема Ларіонова)
1.2 Система керування
2. Розрахунок силової частини
3. Розрахунок системи керування
4. Моделювання перехідного процесу
5. Дослідження стійкості
6. Висновки
7.Література
Додатки
Вступ
Схеми випрямлячів трифазного живлення застосовуються в основному для живлення споживачів середньої й великої потужності. Первинна обмотка трансформаторів таких випрямлячів складається із трьох фаз і з'єднується або в зірку, або в трикутник. Вторинні обмотки трансформатора (їх може бути трохи) також трифазні. За допомогою спеціальних схем з'єднання вторинних обмоток і всього випрямляча можна одержати випрямлення напруга із числом пульсацій за період  , кратним шести. Зі збільшенням числа пульсацій у випрямленій напрузі значно скорочуються габаритні розміри електричних фільтрів, що згладжують, або взагалі відпадає необхідність у них. , кратним шести. Зі збільшенням числа пульсацій у випрямленій напрузі значно скорочуються габаритні розміри електричних фільтрів, що згладжують, або взагалі відпадає необхідність у них.
Випрямлячі трифазного живлення рівномірно навантажують мережа трифазного струму й відрізняються високим коефіцієнтом використання трансформатора.
Схеми випрямлячів трифазного живлення використовуються для живлення статичних навантажень активного й активно-індуктивного характеру, статичних навантажень із проти-ерс., а також динамічних навантажень у вигляді електродвигунів постійного струму. Останній вид навантаження варто розглядати як проти-ерс. з індуктивністю.
Проектування схем вентильних перетворювачів є одним з важливих напрямків у силовий перетворювальної схемотехніці.
Основа проектування сучасних силових перетворювачів - методи розрахунку процесів у силових ланцюгах з вентилями, які по своїй математичній моделі є зручними для аналізу й синтезу перетворювальних схем.
1. Теоретичні відомості про роботу пристрою
1.1 Силова частина
Трифазна вентильна схема (схема Ларіонова).
Вентилі 1,3,5 утворять катодну, а вентилі 2,4,6 - анодну групи (рис.1.1.). З катодної групи струм пропускає той вентиль, до анода якого підводить більша позитивна напруга.
Нумерація вентилів у даній схемі відповідає порядку їхнього вступу в роботу за умови дотримання фазировки трансформатора (рис.1.1.).

Рис.1.1. Схема Ларіонова
У будь-якому проміжку часу повинні бути включені два вентилі – один з катодної, а іншої з анодної групи. Почергова робота різних пар вентилів у схемі приводить до появи на опорі Rd
випрямленої напруги, що складає із частин лінійних напруг вторинних обмоток трансформатора (вісь 2 на рис.1.2) [1, 2].
З рис.1.2 (осі 1 і 2) видно, що моменти комутації збігаються з моментами проходження через нуль лінійних напруг (коли рівні дві фазних напруги).
У проміжку ( 0-01) найбільше позитивне значення має напруга ua
, подаване до анода вентиля 1, а найбільше негативне значення – напруга ub
, що підводиться до катода вентиля 6. Отже, у цьому проміжку одночасно включені вентилі 1 і 6. Через вентиль 1 позитивна напруга ua
підводить до нижнього затискача, а через вентиль 6 негативна напруга ub
підводить до верхнього затискача опору Rd
. Тому випрямлене напруга ud
= ua
- ub
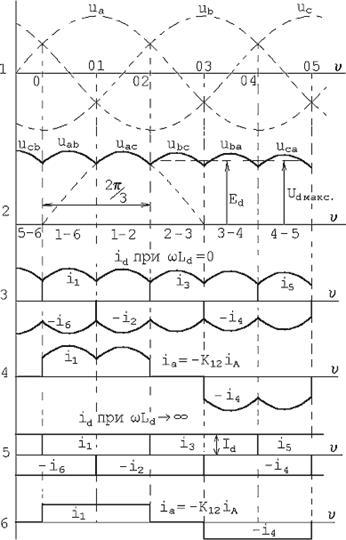
Рис.1.2. Криві струмів і напруги при α
=0.
У точці 01 напруга ub
= uc
, тому з анодної групи включається вентиль 2. Тому що правіше крапки 01 напруга uc
має найбільше негативне значення, вентиль 6 вимикається. У проміжку ( 01-02) одночасно включені вентилі 1 і 2 і випрямлена напруга:
ud
= ua
- uc.
Очевидно, що амплітуда випрямленої напруги:
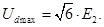
До кожного закритого вентиля прикладене лінійна напруга, тому амплітуда зворотної напруги
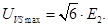
Число пульсацій випрямленої напруги m=
6.
Постійна складова випрямленої напруги (середнє значення) обчислюється для інтервалу повторюваності випрямленої напруги, рівного  : :
 . (1) . (1)
де Е
2
– діюче значення фазної напруги вторинних обмоток трансформатора.
Діюче значення струму вторинної обмотки (вісь 6):
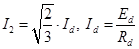 . (2) . (2)
Діюче значення струму первинної обмотки:
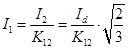 . (3) . (3)
Максимальне значення струму вентиля:
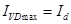 . (4) . (4)
Середнє значення струму вентиля:
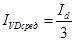 . (5) . (5)
Діюче значення струму вентиля:
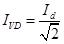 . (6) . (6)
Нехай кут керування  . У трифазній мостовій схемі на керованих вентилях імпульси, що відмикають, надходять із затримкою на кут ,
щодо нулів лінійних напруг або моментів перетинання синусоїд фазних напруг (рис.1.3). . У трифазній мостовій схемі на керованих вентилях імпульси, що відмикають, надходять із затримкою на кут ,
щодо нулів лінійних напруг або моментів перетинання синусоїд фазних напруг (рис.1.3).
У результаті затримки моментів комутації тиристорів на кут α
середнє значення випрямленої напруги, утвореного з відповідних частин лінійних напруг, знижується доти, поки крива миттєвих значень випрямленої напруги ud
залишається вище нуля, що відповідає діапазону зміни кута керування  , випрямлений струм id
буде безперервним поза залежністю від характеру навантаження. Тому при кутах , випрямлений струм id
буде безперервним поза залежністю від характеру навантаження. Тому при кутах  середнє значення випрямленої напруги для активного й активно-індуктивного навантаження буде дорівнює середнє значення випрямленої напруги для активного й активно-індуктивного навантаження буде дорівнює
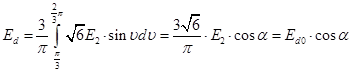 . (7) . (7)
При кутах 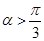 і активному навантаженні в напрузі ud
і струмі id
з'являються інтервали з нульовим значенням (рис.1.4.), тобто наступає режим роботи з переривчастим випрямлений струмом. і активному навантаженні в напрузі ud
і струмі id
з'являються інтервали з нульовим значенням (рис.1.4.), тобто наступає режим роботи з переривчастим випрямлений струмом.
Середнє значення випрямленої напруги для цього випадку може бути виражене в такий спосіб:
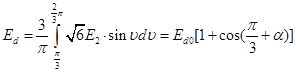 ,(8) ,(8)
де
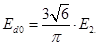

Рис.1.3. Діаграми струмів і напруг при кутах  . .
У режимі з переривчастим струмом id
для забезпечення роботи даної схеми, а також для її первісного запуску на вентилі схеми варто подавати здвоєні імпульси, що відмикають, з  інтервалом або одиночні, але із тривалістю, більшої, інтервалом або одиночні, але із тривалістю, більшої,  ніж . Це пояснюється тим, що для утворення замкнутого ланцюга протікання струму id необхідно забезпечити одночасне включення вентиля анодної групи й вентиля катодної групи. ніж . Це пояснюється тим, що для утворення замкнутого ланцюга протікання струму id необхідно забезпечити одночасне включення вентиля анодної групи й вентиля катодної групи.
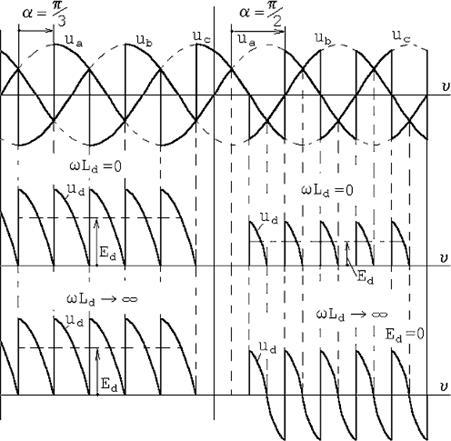
Рис.1.4. Діаграми напруг при кутах 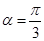 і і 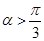
При зміні кута  від 0 до від 0 до  регулювальна характеристика для активного й активно-індуктивного навантаження описується формулою: регулювальна характеристика для активного й активно-індуктивного навантаження описується формулою:

При активно-індуктивному навантаженні й кутах 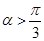 , якщо , якщо  або відношення або відношення 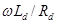 таке, що забезпечується режим безперервного струму id
, середнє значення випрямленої напруги також визначається по формулі: таке, що забезпечується режим безперервного струму id
, середнє значення випрямленої напруги також визначається по формулі:
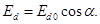
При 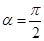 середнє значення середнє значення  стає рівним нулю, виходить, це відповідає рівності площ позитивної й негативної ділянок кривій випрямленої напруги, що свідчить про відсутність у ньому постійної складової (крива 2 на рис.1.5). стає рівним нулю, виходить, це відповідає рівності площ позитивної й негативної ділянок кривій випрямленої напруги, що свідчить про відсутність у ньому постійної складової (крива 2 на рис.1.5).
Починаючи з кута 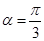 при активному навантаженні регулювальна характеристика описується формулою (крива 1 на рис.2.5): при активному навантаженні регулювальна характеристика описується формулою (крива 1 на рис.2.5):
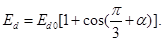
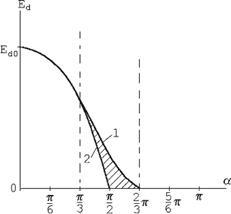
Рис.1.5. Регулювальні характеристики: 1 - при активному навантаженні; 2 - при активно-індуктивному навантаженні.
Заштрихована область на рис.1.5 відповідає сімейству регулювальних характеристик у режимі з переривчастим струмом id
при різних значеннях 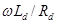 . .
Приймемо індуктивність Ld
настільки великий, що струм навантаження id
до моменту відмикання наступного вентиля не встигає пройти через нуль. Коли струм через нуль не проходить, він наростає від інтервалу до інтервалу й установлюється протягом ряду періодів (звичайно трьох, чотирьох).
У трифазній мостовій схемі до навантаження R
-L
підключена напруга:

де  , а кут природного включення вентилів при , а кут природного включення вентилів при  становить становить 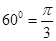 . .
Струм через навантаження визначається диференціальним рівнянням
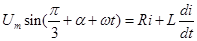 (9) (9)
Загальний інтеграл рішення рівняння (9)
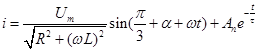 (10) (10)
де 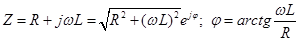 - кут навантаження; - кут навантаження; 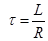 - постійна часу ланцюга навантаження; - постійна часу ланцюга навантаження;  – постійна інтегрування, обумовлене в кожному конкретному випадку з початкових умов. – постійна інтегрування, обумовлене в кожному конкретному випадку з початкових умов.
Для визначення струму в будь-якому інтервалі часу зручно скористатися різницевими рівняннями.
У загальному випадку до навантаження R-L
може бути підключена напруга із противо ЕДС

де E0
– противо-ерс, наприклад, акумуляторна батарея або якір двигуна постійного струму. При впливі противо-едс можна одержати режим переривчастих струмів, де рівняння (9) і (10) недійсні.
1.2 Система керування
Система керування (СУ) випрямляча призначена для формування керуючих імпульсів необхідної амплітуди й тривалості; для твердої синхронізації їх з напівперіодами фазних напруг; для розподілу керуючих імпульсів по трьох каналах, відповідно до числа фаз випрямляча; для стабілізації вихідної напруги шляхом автоматичної зміни кута керування α
при впливі дестабілізуючих факторів.
Принципова схема, шестиканальної системи керування, у якій реалізований метод ШІМ-1, наведена на рис.1.6. Схема побудована при використанні операційних підсилювачів загального призначення.
Синусоїдальна напруга фази А
, що знімається c додаткової (синхронізуючої) обмотки силового трансформатора TV1
,надходить на вхід синхронізатора, зібраного за схемою симетричного двостороннього обмежника напруги на діодах VD1
, VD2
.Через нелінійність вольтамперных характеристик діодів на виході синхронізатора формується трапецеїдальна напруга з амплітудою U
огр
, рівної спаданню напруги на відкритому діоді й тривалістю фронту ωtф
. Прямий струм через діоди обмежується резисторами R1
, R2
.
З виходу обмежника трапецеїдальний сигнал надходить на вхід операційного підсилювача DA1
з метою збільшення крутості фронтів і наданні напрузі прямокутної форми з амплітудою U
п
.
Дана напруга призначена керування польовим транзистором VТ1
.
Для того щоб час відкритого стану транзистора було багато менше періоду СУ включає RC-
ланцюжок, що складається з C1
і R3
.
Під час відкритого стану транзистора VТ1
відбувається заряджання конденсатора С2
до вихідної напруги підсилювача зворотного зв'язка (ПЗЗ), зібраного на мікросхемі DA4.
Розряджається конденсатор постійним струмом. Джерело струму складається з ОУ DA2,
резисторів R4
, R5
, R6
і транзистора VТ2.
Напруга конденсатора С2
надходить на вхід, що інвертує, компаратора DA
3 і рівняється з порівняльним значенням.
Доти поки на конденсаторі буде напруга на виході компаратора буде 0. Дана напруга відображає кут регулювання.
Позитивний імпульс вихідної напруги компаратора через обмежуючий резистор R7
надходить у ланцюг бази транзистора VТ3
, що виконує функцію вихідного підсилювача потужності. При відмиканні транзистора в його колекторному ланцюзі протікає імпульс керуючого струму з амплітудою Iу0
, під дією якого світлодіод оптрона випромінює світловий імпульс і переводить силовий тиристор фази А
у включений стан. Для обмеження амплітуди керуючого струмі включається резистор R9
. В інтервалі часу, коли вихідна напруга компаратора негативно, транзистор VT3
закритий.
Стабілізація вихідної напруги здійснюється ланцюгом зворотного зв'язка, що складає з вимірювального елемента, джерела опорного (еталонного) напружена й підсилювача зворотного зв'язка. Функцію вимірювального елемента в схемі виконує дільник напруги R14
, R15
, R16
, підключений до вихідних клем випрямляча. Частина вихідної напруги, що знімається з нижнього плеча дільника, рівняється з еталонною напругою опорного стабілітрона VD3
.
Необхідний струм стабілізації встановлюється резистором R17
.
Різниця між вихідною й еталонною напругою підсилюється підсилювачем зворотного зв'язка (мікросхема DA4
) надходить через транзистор VТ1
на конденсатор С2
, а також на входи компараторів каналів формування імпульсів фаз B
і С.
Необхідний коефіцієнт підсилення ПЗЗ установлюється резисторами R11
, R12
. При зміні напруги на навантаженні під дією дестабілізуючих факторів, наприклад при його збільшенні, напруга на не вході, що інвертує, ПЗЗ зростає. Це приведе до збільшення напруги на його виході, внаслідок чого конденсатор С2
буде довше розряджатися, тобто кут α
буде зростати. У результаті вихідна напруга зменшиться майже до первісної. При зменшенні напруги на навантаженні (наприклад, внаслідок зменшення напруги в мережі або збільшення струму навантаження) напруга на виході ПЗЗ зростає й кут керування α
зменшується.
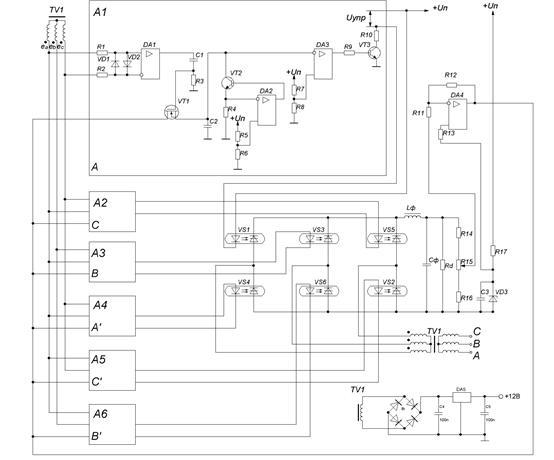
Рис.1.6.
2. Розрахунок силової частини
Трифазна схема Ларіонова зображена на рис. 2.1.
Вихідні дані:
f=
50 Гц;
UC
=
220 B;
δUC
=
+/-10% B;
UH
=
36 B;
δUH
=
+/-1% B;
ΔUH
=
+/-10% B;
Кп = 2%;
Рн = 2000 Вт;
Рн хв = 200 Вт.
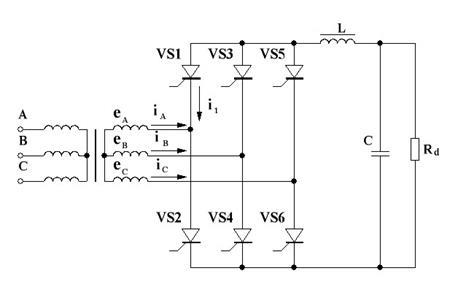
Рис. 2.1.
Розрахунок граничних значень випрямленої напруги й мережного:
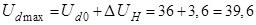 B;
B;
 B;
B;
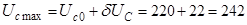 B;
B;
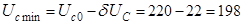 B.
B.
Розрахунок діапазону регулювання випрямляча:
Дана схема трифазного випрямляча буде працювати в режимі безперервного струму навантаження й позитивного выпрямленного напруги, при цьому кут регулювання змінюється в межах 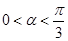 .
.
Регулювальна характеристика описується вираженням:

Задаємося мінімальним кутом регулювання  .
.
Визначаємо 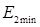 при
при 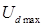 й
й  :
:
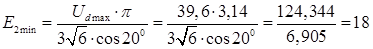 B.
B.
Коефіцієнти зміни живлячої напруги (Е1
=UC
):
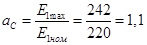 ;
;
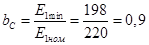 .
.
Номінальна й максимальна фазна напруга на вторинній обмотці:
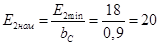 B;
B;
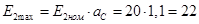 B;
B;
Максимальний кут регулювання  :
:
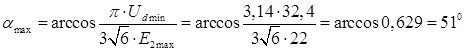 ;
;
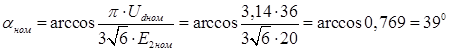 .
.
Діапазон регулювання 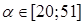 . .
Розрахунок і підбор вентилів:
Середній струм тиристорів випрямляча:
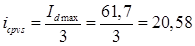 А;
А;
 А;
А;
Діюче значення струму тиристорів:
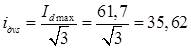 А;
А;
Зворотна напруга на вентилях випрямляча:
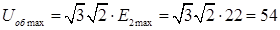 В. В.
Тиристори: ТЕ 132-40-3
з параметрами: максимальний середній струм  А; струм керування А; струм керування 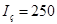 мА; максимальний струм керування мА; максимальний струм керування 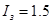 А; максимальна зворотна напруга А; максимальна зворотна напруга 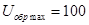 В; максимальне спадання напруги у відкритому стані В; максимальне спадання напруги у відкритому стані  В; діапазон робочої температури В; діапазон робочої температури 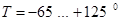 С. С.
Розрахунок LC
- фільтра.
Для розрахунку фільтра необхідно знайти значення коефіцієнта пульсацій по першої гармоніки:
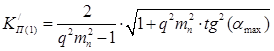 ;
;
Де mn
= 1-1- число пульсацій, q = 1-1- № гармоніки.
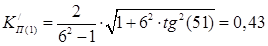 ;
;
Розрахуємо значення індуктивності L
:
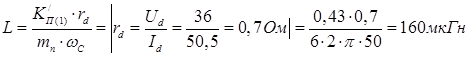 ;
;
Добутку LC
:
 ; де
; де 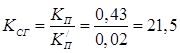 ;
;
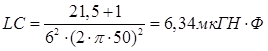 ; ;
Розрахунок значення ємності конденсатора З
:
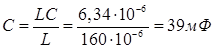 ;
;
Вибираємо електролітичний конденсатор фірми Panasonic
ECOSIAA394DA
.
Розрахунок дроселя L
:
Початкові умови:
L
= 160 мкГн;
f
= 300 Гц;
Ід
=62А;
Сердечник стрічковий броньового типу. Магнітопровід зі сталі З423 з товщиною стрічки 0,15мм. Індукція Вm
= про,9 Тл.
Розрахунок ведемо за методикою, викладеної в книзі Мелешина В.И. "Транзисторна перетворювальна техніка". З таблиці для даного типу сердечника й магнітопроводу записуємо значення Kj
= 366 А/див2
і в
= -0,12.
Діюча напруга на обмотці:
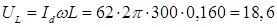 В;
В;
Добуток ScSo
при коефіцієнті заповнення вікна Ки = 0,4:
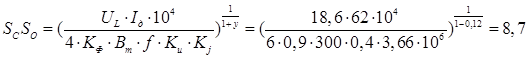 см4
;
см4
;
З довідника вибирається сердечник ШЛ 12*25 з параметрами:
а
= 12, в
= 25, з
=12, h
= 30 мм, So
= 3,6 див2
, ScSo
= 10,8 див4
, lc
= 10,2 див, активний перетин сердечника ScKc
=2,42 див2
, ScKcSo
= 8,712 див4
.
Число витків дроселя:
 ;
;
Знаходження повітряного зазору:
 мм.
мм.
Коефіцієнт витріщання магнітного потоку в зазорі:
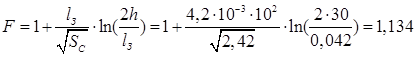 ;
;
Уточнення необхідного числа витків:
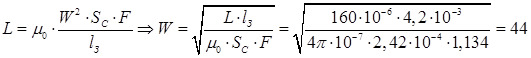 ;
;
Визначення щільність струму:
 А/мм2
. А/мм2
.
Розрахунок перетину проведення:
 мм2
. мм2
.
Вибираємо проведення ПЭТВ перетином 2,217 мм2
і з питомим опором 0,00791.
Розрахунок опору дроселя:
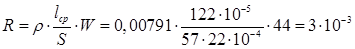 Ом. Ом.
Розрахунок трансформатора.
Коефіцієнт трансформації:
 . .
Габаритна потужність трансформатора:
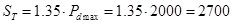 ВА. ВА.
Тип магнітопроводу: ТЛ25х40.
Активний опір трансформатора  й індуктивність розсіювання й індуктивність розсіювання  обмоток трансформатора: обмоток трансформатора:
 ; ;
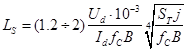 ; ;
де  — щільність струму в обмотках трансформатора, А/мм2
; — щільність струму в обмотках трансформатора, А/мм2
;
 — амплітуда магнітної індукції, Т. — амплітуда магнітної індукції, Т.
Визначаємо  , ,  : : 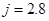 А/мм2
, А/мм2
,  Т. Т.
Визначаємо  , ,  : :
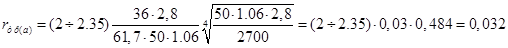 Ом; Ом;
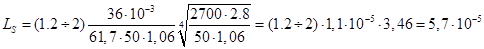 Гн. Гн.
Визначимо  : :
 Ом. Ом.
Визначимо  : :
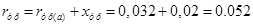 Ом. Ом.
Максимальне значення струмів первинної й вторинної обмоток трансформатора:
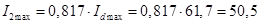 А; А;
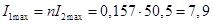 А. А.
3. Розрахунок системи керування
Напругу Uac
обираємо рівною 10В. Для того, щоб струм на вході операційного підсилювача був 10мА обираємо резистори R1
, R2
по 0,5 кОм кожний. Діоди вибираємо ВА607, що відповідають схемному рішенню. Операційний підсилювач обираємо МС34063.
Розрахунок RC
-ланки:
Час імпульсу встановлюємо 10мкс, номінал резистора  =5кОм, тоді ємність конденсатора обчислюється: =5кОм, тоді ємність конденсатора обчислюється:
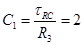 нФ. нФ.
Польовий транзистор VT1
вибираємо IRML2402.
Конденсатор С2
повинен розрядитись за 0,47 мс струмом джерела струму в 0,1 мА визначається за формулою:
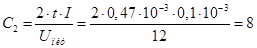 нФ. нФ.
Розрахунок резисторів R4
,R5
,R6
:
Обираємо напругу на резисторі R4
рівною 1 В,  кОмж кОмж
Обираємо напругу на резисторі R6
рівною 1 В, опір R6
= 1 кОм, тоді R5
= 1 1кОм.
Розрахунок резисторів R7
,R8
:
Резистори R7
,R8
повинні забезпечити рівень компорирування на половини напруги живлення, їх номінали однакові, по 10кОм.
Розрахунок підсилювача на біполярному транзисторі VT3
:
Біполярний транзистор VT3
вибираємо ВС848.
Резистор
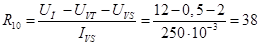 Ом; Ом;
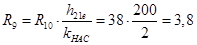 кОм. кОм.
Розрахунок підсилювача сигналу помилки:
Коефіцієнт підсилення обираємо рівним 20.
R11
= 100 кОм, R12
= 20* R11
=2 МОм, R13
= R11
= 100 кОм
Розрахунок формувача опорної напруги:
Напруга на R16
:
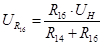 ; ;
Задаємося 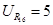 В, R16
= 5 кОм, тоді R14
= 31 кОм, а R15
= 0,1R16
= 500 Ом, В, R16
= 5 кОм, тоді R14
= 31 кОм, а R15
= 0,1R16
= 500 Ом,
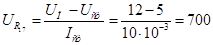 Ом. Ом.
Конденсатор С3
обираємо 0,22 мкФ.
Діаграми роботи системи керування (для одного вентиля) зображено на рис. 3.1.

Рис. 3.1.
4. Моделювання перехідного процесу
Для моделювання процесів в схемі, ми маємо скласти диференційні рівняння, що описують роботу схеми. Перед тим як скласти систему рівнянь необхідно зобразити схему заміщення і обумовити спрощення моделей елементів. Всі ветилі мають однакові параметри та однаковий опір у відкритому стані, дросель замінюється індуктивністю та послідовно під’єднаним опором, напруга на всіх обмотках трансформатора однакова, лише зміщена по фазі, враховується опір обмоток, опір конденсатора не враховуємо.
Схема заміщення зображена на рис.4.1.

Рис.4.1.
Оскільки форма напруги періодична то достатньо дослідити лише два відрізки часу коли відкритими є два вентильних елемента протягом  . Періодом Т будемо вважати сусідні моменти природної комутації. Кут керування обираємо номінальний . Періодом Т будемо вважати сусідні моменти природної комутації. Кут керування обираємо номінальний  . Для зручності перейдемо в області часу, кут . Для зручності перейдемо в області часу, кут  замінимо на замінимо на  с и в радіани с и в радіани  . .
Протягом періоду Т структура схеми заміщення не міняється, змінюється лише напруга U
.
Система диференційних рівнянь має наступній вигляд:
 ; ;
В залежності від інтервалу напруга U
буде рівною:
 , ,  . .
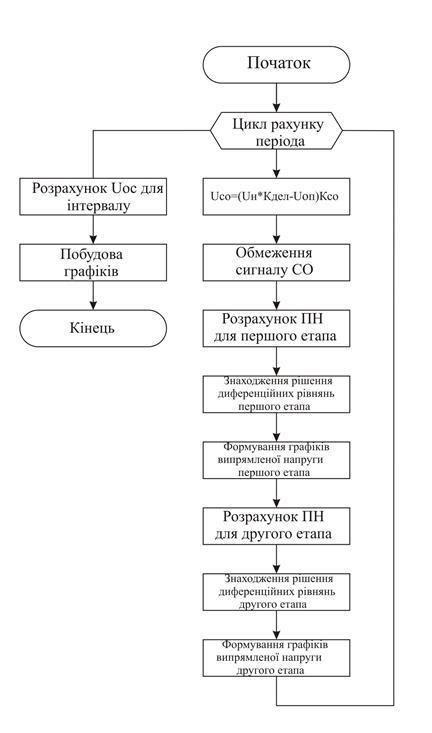
Отриману систему рівнянь використаємо при моделюванні перехідних процесів у схемі. Моделювання будемо здійснювати за допомогою програми MathLab 7.5. Блок-схема програми моделювання перехідних процесів у схемі наведено у Додатку №1.
В результаті моделювання були отримані графіки струму індуктивності, напруги на ємності, випрямленої напруги та основних напруг системи керування: ГПН та сигналу помилки.
Графік перехідного процесу показано на рис. 4.2.

Рис. 4.2.
Більш детально графіки в момент пуску та для усталеного режиму показано на рис. 4.3 та 4.4 відповідно.

Рис. 4.3.
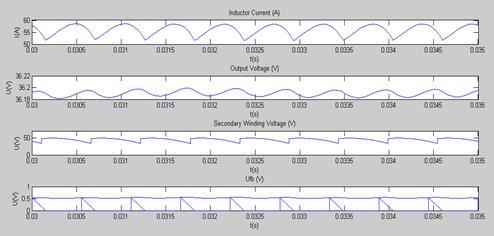
Рис. 4.4.
5. Дослідження стійкості
Дослідження стійкості будь-якої системи можна розбити на етапи:
1. Складання рівнянь на окремих інтервалах роботи;
2. Об’єднання отриманих рівнянь;
3. Лінеаризація рівнянь відносно однієї із змінних стану;
4. Знаходження розв’язку усталеного режиму;
5. Дослідження стійкості по характеристичному рівнянню.
Рівняння для кожного інтервалу роботи схеми ми знайшли в попередньому пункті, при досліджені перехідного процесу:
Для зручності написання систем об’єднаємо послідовно підключені опори  Ом. Ом.
1. 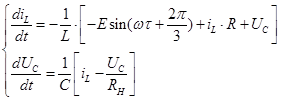 ; ;
2. 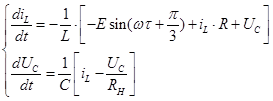 . .
Систему керування можна описати наступною системою рівнянь:
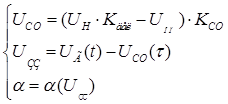 , ,
де,  - сигнал помилки, - сигнал помилки,  - вихідна напруга, - вихідна напруга,  - опорна напруга, - опорна напруга,  - сигнал зворотнього зв’язку, - сигнал зворотнього зв’язку,  - коефіцієнт підсилення , - коефіцієнт підсилення ,  - функція, що приймає значення 1 при високому рівні на виході СК, а 0 – при низькому. - функція, що приймає значення 1 при високому рівні на виході СК, а 0 – при низькому.
Використаємо  для того, щоб об’єднати системи рівнянь для двох інтервалів роботи схеми. для того, щоб об’єднати системи рівнянь для двох інтервалів роботи схеми.
 . .
Представимо отриману систему рівнянь у матричній формі:
 , ,
де
 , ,  , , . .
Лінеаризуємо отриману систему в "малому". Знайдем диференціали по змінним стану від правої і лівої частин системи. Ввівши позначення  , ,  , отримаємо рівняння , отримаємо рівняння
 , ,
де  , , , , . .
Оскільки матриця  не залежить від змінних стану не залежить від змінних стану  та та  , то , то  . .
 , ,
 , ,
де  – –  -функція Дірака. -функція Дірака.
Використаємо наступну властивість  -функції -функції
 , ,   , ,
 ; ;
 . .
оскільки  , то можемо записати: , то можемо записати:
 . .
Використовуючи властивість  -функції -функції  , визначимо значення добутку: , визначимо значення добутку:
 . .
Оскільки

то  ; ;
 , ,
де матриця S
має вигляд:
 . .
Визначимо матриці А1
та А2
:
 , ,  , , . .
Знайдемо розв’язок рівняння на інтервалі постоянства структури з використанням неперервного перетворення Лапласа на інтервалі  . .
 ,де ,де  . .
Застосуємо неперервне перетворення Лапласа до лівої і правої частини рівняня:
 . .
Рішаючи отримане матричне рівняння отримаємо:
 , де , де  – зворотня матриця; – зворотня матриця;
 , , . .
Для переходу в часову область використаємо зворотнє перетворення Лапласа, в результаті чого отримаємо:
 , ,
де  . .
Знайдемо розв’язок рівняння на інтервалі постоянства структури з використанням неперервного перетворення Лапласа на інтервалі  : :
 ,де ,де  . .
Застосуємо неперервне перетворення Лапласа до лівої і правої частини рівняня:
 . .
Рішаючи отримане матричне рівняння отримаємо:
 , ,
де  – зворотня матриця. – зворотня матриця.
Для переходу в часову область використаємо зворотнє перетворення Лапласа, в результаті чого отримаємо:
 ; ;
де  . .
Підставимо в рівняння для інтервалу  значення часу значення часу  , а в рівняння для інтервалу , а в рівняння для інтервалу  – значення часу – значення часу  , після чого підставимо перше рівння у друге: , після чого підставимо перше рівння у друге:
 ; ;
 ; ;
 . .
Отримане рівняння визначає стійкість у "малому" початкової нелінійної системи в околі установившогося режиму  . .
Застосуємо дискретне перетворення Лапласа до отриманого рівняння:
 , ,
де  – дискретне зображення Лапласа – дискретне зображення Лапласа  ; ;  – початкове значення вектору – початкове значення вектору  : :  . Перетворивши отримане рівняння отримаємо: . Перетворивши отримане рівняння отримаємо:
 . .
В результаті відкриття визначника  , знаходимо характеристичний многочлен: , знаходимо характеристичний многочлен:
 ; ;

 . .
Зробимо заміну змінних  ; ;
 ; ;
 , , . .
Корені даного рівняння знаходяться в середині кола одиничного радіуса і тому можна зробити висновок, що дана схема являється стійкою.
6. Висновки
У даній курсовій роботі був виконаний розрахунок перехідного процесу, що виникає при включенні пристрою, і стійкості в "малому" сталому режимі, на прикладі трьохфазного мостового випрямляча із ШІМ першого роду. При виконанні курсової роботи була спроектована принципова схема пристрою. Схему такого випрямляча можна віднести до схем зі постійною структурою й аналізувати неї на інтервалах роботи, де змінюється напруга.. Для розрахунку перехідного процесу були складені диференціальні рівняння й по них побудовані графіки, елементи силової частини при цьому замінялися їхніми ідеалізованими моделями. Також був проведений розрахунок стійкості системи, що показав, що дана система є стійкою.
7. Література
1. Г.С. Найвельт и др. "Источники электропитания радиоэлектронной аппаратуры. Справочник". М.: Радио и связь, 1985
2. Перетворювальна техніка. Частина 1: Підручник./ В. С. Руденко, В. Я. Ромашко, В. Г. Морозов. – К.: ІСДО, 1996.– 262 с.
3. Замкнутые системы преобразования электрической энергии. Под ред. Д-ра техн. наук В.Я. Жуйкова. – Киев, "Техника", 1989.
4. Методические указания к курсовой работе по курсу "Преобразовательная техника" для студентов специальности "Промышленная электроника" всех форм обучения. Сост.: В. С. Руденко, В. Г. Морозов, В. Я. Ромашко. – Киев: КПИ, 1984. – 56с.
Додаток 1.
Додаток 2.
function main;
Rv1=37*10^(-3);
Rv2=Rv1;
Rdr=80*10^(-3);
Rd=0.648;
Ld=160*10^(-6);
C=39*10^(-3);
E=20*sqrt(6);
U0=0;
I0=0;
t=0;
K=-3500;
U_start=0;
Kfb=20;
Pi=3.1415;
L=Pi/7;
s=0;
Z=0;
Y=[0, 0];
t=0;
PhaseShift=2*Pi/3;
Ufb=0;
Uref=5;
D=0;
Dx=0;
Dt=0;
Dtx=0;
Ufb=0;
O=0;
P=0;
w=2*Pi*300;
for f=1:100
s=0;
Z=0;
Dtx=0;
Dx=0;
U_start=(Y(end,2)*5/36-Uref)*Kfb;
if (U_start<0)
U_start=0;
end
Dtx(1)=0;
Dtx(2)=-U_start/K;
if (Dtx(2)>((Pi/3)/w))
Dtx(2)=(Pi/3)/w;
end
Dx(1)=U_start;
Dx(2)=K*Dtx(2)+U_start;
Y0=[Y(end,1),Y(end,2)];
[s,Z]=ode113(@F_first, [0 (Dtx(2)+10^-8)], Y0);
s=s+t(length(t));
Y=[Y;Z];
t=[t;s];
n=0;
Ox=0;
Px=0;
for x=0:0.000001:Dtx(2)+10^-8
n=n+1;
Ox(n)=E*sin(w*x+PhaseShift);
Px(n)=x;
end
Px=Px+P(length(P));
P=[P, Px];
O=[O, Ox];
PhaseShift=PhaseShift-Pi/3;
PhaseShift=PhaseShift+(Dtx(2)+10^-8)*w;
Dtx(3)=(Pi/3)/w;
Dx(3)=0;
s=0;
Z=0;
Y0=[Y(end,1),Y(end,2)];
[s,Z]=ode113(@F_first, [0 (Dtx(3)-Dtx(2))+10^-8], Y0);
s=s+t(length(t));
Y=[Y;Z];
t=[t;s];
n=0;
Ox=0;
Px=0;
for x=0:0.000001:(Dtx(3)-Dtx(2))
n=n+1;
Ox(n)=E*sin(w*x+PhaseShift);
Px(n)=x;
end
Px=Px+P(length(P));
P=[P, Px];
O=[O, Ox];
PhaseShift=PhaseShift+(Dtx(3)-Dtx(2))*w;
Dtx=Dtx+Dt(length(Dt));
D=[D, Dx];
Dt=[Dt, Dtx];
end
for x=1:length(t)
Ufb(x)=(Y(x, 2)*5/36-Uref)*Kfb;
if (Ufb(x)<0)
Ufb(x)=0;
end
end
I=Y;
I(:, 2)=[];
subplot(4,1,1);
plot(t,I);
xlabel('t(s)');
ylabel('I(A)');
title('Inductor Current (A)');
hold on;
I=Y;
I(:, 1)=[];
subplot(4,1,2);
plot(t,I);
title('Output Voltage (V)');
xlabel('t(s)');
ylabel('U(V)');
subplot(4,1,3);
plot(P,O);
xlabel('t(s)');
ylabel('U(V)');
title('Secondary Winding Voltage (V)');
subplot(4,1,4);
plot(t,Ufb);
hold on;
plot(Dt, D);
title('Ufb (V)');
xlabel('t(s)');
ylabel('U(V)');
function G = F_first(t, y)
Ud=E*sin(w*t+PhaseShift);
G=[-1/Ld*(-Ud+y(1)*(Rv1+Rv2+Rdr)+y(2)); 1/C*(y(1)-y(2)/Rd)];
end
end
|