Счетчики и делители
1. Понятие и назначение счетчика
Счетчик предназначен для подсчета количества единиц информации (счетных импульсов). Поступление единицы информации заключается в воздействии на вход счетчика перепада напряжения 0 – 1 при входе или 1 – 0 при инверсном входе. Так как один импульс содержит тот и другой перепады, то его и отождествляют с единицей информации независимо от типа входа счетчика.
Счетчик имеет Kn
устойчивых состояний, каждое из которых повторяется после подсчета Kn
счетных импульсов. Иначе говоря, счет импульсов осуществляется с коэффициентом (модулем) пересчета Kn
.
По способу кодирования числовой информации различают счетчики с позиционным (единичным, двоичным, десятичным и т.д.) и непозиционным (например, в кодах Грея) кодированием. В счетчиках с позиционным кодированием числовое выражение текущего состояния определяется формулой:
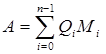
где n – количество разрядов; Qi
– логическое значение разряда (Qi
=0,1); Mi
– вес i-го разряда.
В счетчиках с непозиционным кодированием разряды не имеют постоянныхвесов, и числовое выражение состояния предписывается каждому набору значений Qi
. Этот тип счетчиков встречается на практике существенно реже, чем счетчики с позиционным кодированием.
Ниже рассматриваются наиболее распространенные счетчики, ведущие счет в двоичной системе счисления, - двоичные счетчики основу их построения положены n счетных триггеров. Каждому из них ставится в соответствие один определенный вес из набора: 20
, 21
,...,2n
-1
. Количество поступивших импульсов представляется в виде суммы
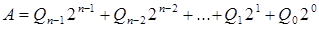
или для краткости записи – в виде позиционного набора Qn
-1
Qn
-2
… Q1
Q0
. Максимальный коэффициент пересчета двоичного счетчика Kn
=2n
.
Счетчики подразделяются еще по другим классификационным признакам. По назначению различают суммирующие, вычитающие реверсивные; по способу запуска – асинхронные и синхронные; по способу организации переноса – с последовательным, сквозным и параллельным переносами.
Основными параметрами счетчиков являются: разрешающая способность, время установления и емкость.
Разрешающая способность—это минимальный период следования счетных импульсов Tст
, при которых сохраняется работоспособность счетчика. Обратная величина
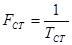
характеризует максимальную частоту счета.
Время установления Tуст
– это интервал между началом подачи на вход счетного импульса и моментом окончания самого продолжительного переходного процесса в счетчике.
Параметры Tст
и Tуст
характеризуют быстродействие счетчика.
Емкость счетчика определяется максимальным числом импульсов, которое он может зарегистрировать. Численно емкость равна коэффициенту пересчета Kп
.
Делители—это те же счетчики, но имеют, как правило, один выход, на котором появляется импульсный сигнал после каждых Kп
счетных импульсов. Нередко предусматривается возможность изменять коэффициент деления Kп
с помощью специального управляющего кода. В принципе делители можно строить и на основе двоичных счетчиков, подключив к выходам дешифратор какого-либо одного состояния.
В большинстве практических случаев интегральные пересчетные устройства делаются комбинированными – счетчиками-делителями. С этой целью счетчик дополняют дешифратором старшего состояния, выходной сигнал которого может быть использован как сигнал переноса при наращивании разрядности с помощью нескольких микросхем, либо как выходной сигнал делителя.
2. Счетчики с последовательным переносом
2.1 Суммирующие счетчики
Суммирующий счетчик должен функционировать так, чтобы при поступлении на его вход одного импульса записанное в нем число увеличилось на единицу. Принцип построения суммирующего счетчика следует из правила прибавления к двоичному числу единицы. В соответствии с этим правилом, например, трехразрядный счетчик должен последовательно принимать состояния 000, 001, 010, 011, 100, …, 111.
Видно, что триггер младшего разряда переключается каждым счетным импульсом, т.е. входом счетчика служит вход этого триггера. Состояния второго и третьего триггеров меняются соответственно каждым вторым и четвертым импульсом. Это обеспечивается последовательным соединением триггеров.
Из правила прибавления к двоичному числу единицы также известно, что изменение значения i-го разряда происходит тогда, когда до прибавления очередной единицы все предыдущие разряды были единицами. Отсюда следует правило: если триггеры имеют прямой счетный вход, то он подключается к инверсному выходу предыдущего триггера; если имеет инверсный вход, то он подключается к прямому выходу.
Иллюстрирующий пример трехразрядного суммирующего счетчика с временными диаграммами работы и условным изображением приведен на рис. 1. Счетчик может принимать 8 различных состояний, которые повторяются через каждые 8 входных импульсов (Kn
=8). С наибольшей частотой переключается триггер младшего разряда, следовательно, разрешающая способность счетчика определяется временем задержки переключение триггера (Тст
=Ттг
). Это положение распространяется на все типы двоичных счетчиков.
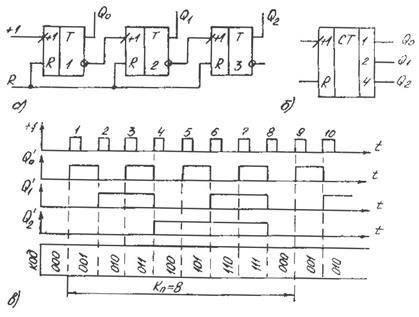
Рисунок 1 – схема (а), условное графическое обозначение (б) ивременные диаграммы трехразрядного суммирующего счетчикас последовательным переносом.
Данный счетчик называют счетчиком с последовательным переносом, так как переключение триггера i-го разряда происходит в результате последовательного переключения всех предыдущих триггеров младших разрядов, т. е. информация распространится по цепочке триггеров последовательно. Время установления счетчика
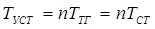 . .
Это говорит о том, что если, например, необходимо снимать информацию после каждого входного импульса, период следования их должен быть T>nTТГ
.
Существенное ухудшение быстродействия с ростом разрядности – основнй недостаток счетчиков с последовательным переносом.
2.2 Вычитающие счетчики
При подаче на вход вычитающего счетчика одного счетного импульса ранее записанное в нем число уменьшается на единицу.Принципы построения вычитающих счетчиков основаны на правилах вычитания двоичных чисел и отличаются от принципов построения суммирующих счетчиков лишь тем, что если триггеры имеют прямой вход +1, то его подключают к прямому выходу предыдущего триггера, если вход инверсный, то подключают к инверсному выходу.
На рис. 2 приведен пример, аналогичный рис. 1. Здесь дополнительный вход S позволяет предварительно устанавливать все триггеры в единичное состояние.

Рис.2
Заметим, что данный счетчик можно рассматривать как суммирующий, а суммирующий (рис. 1) — как вычитающий при инвертировании выходных сигналов Qi
, или съеме информации с выходов Qi
.
2.3 Реверсивные счетчики
Они могут работать как в режиме суммирования, так и вычитания Переключение режимов осуществляется коммутацией счетных входов всех триггеров (кроме триггера младшего разряда) инверсным или прямым выходам предыдущих триггеров (рис. 3). Переключение режима выполняет сигнал разрешения Е'. При Е'=1 прямой вход i-го триггера коммутируется к прямому выходу (i – l)-го триггера, что соответствует режиму вычитания. При E’=0 вход подключается к инверсному выходу, и триггер становится суммирующим.
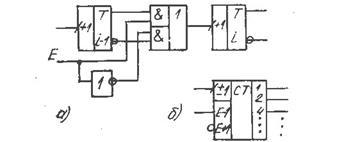
Рис. 3
Универсальность реверсивного счетчика достигается ценой введения дополнительно n-1 логических элементов и ухудшения быстродействия:

где tЗД.СР
– среднее время задержки переключения ЛЭ И-ИЛИ.
Заметим, что правило соединения информационных входов триггеров для получения суммирующих и вычитающих счетчиков распространяется и на счетчики с ускоренным переносом. Поэтому с целью сокращения материала ниже рассматриваются счетчики только суммирующего типа.
3. Счетчики со сквозным переносом
Как известно, триггер i-го разряда переключается, если (i - 1)-й триггер к моменту поступления на его вход очередного счетного сигнала T’i
-1
находился в единичном состоянии, т.е. имеет место Q’i
-1
T’i
-1
= 1. Поэтому с целью ускорения переноса можно входной сигнал T’i
‑1
пропустить на вход i-го триггера с помощью элемента И, минуя (i-1)-й триггер (рис 4).
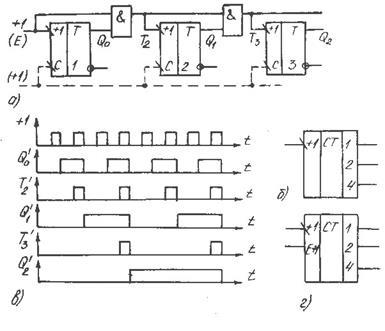
Рис. 4
Триггеры могут быть асинхронными и синхронными. Соответственно этому счетчики получаются асинхронными или синхронными. Счетчик на рис. 4 будет синхронным, если в качестве счетного входа использовать вход синхронизации С, показанный пунктиром.
Из временных диаграмм для асинхронного счетчика, представленных на рис. 4 в, видно, что благодаря схеме переноса на входы второго, третьего и т. д. триггеров транзитом передаются соответственно каждый второй, четвертый и т.д. входные импульсы. При этом прохождение импульсов на вход последнего триггера задерживается на время переноса
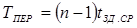 . .
Время установления счетчика
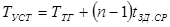 . .
Принимая во внимание, что время задержки прохождения сигнала через ЛЭ И меньше, чем через триггер, выигрыш в быстродействии у счетчиков со сквозным переносом по сравнению со счетчиками с последовательным переносом очевиден. Однако здесь, больше объем оборудования.
У синхронного счетчика со сквозным переносом счетным входом является объединенный вход синхронизации Cвсех триггеров, благодаря чему они переключаются одновременно. Информационный вход первого триггера становится входом разрешения режима счета Е (на рис. 4, а обозначение входов для данного варианта показано в скобках, а условное изображение приведенона рис. 4,г). При E’ = 1 все сигналы T’I
=0, и счетчик находится в режиме хранения. При Е' = 1 устанавливается режим счета.
Время переноса и время установления здесь такие же, как и у асинхронного счетчика. Однако поскольку в асинхронном счетчике в течение всего времени TУСТ
идет непрерывное (с задержкой tЗД.СР
) переключение триггеров, то для съема информации необходимо дополнительное время, т.е. увеличение периода следования входных импульсов. В синхронном счетчике триггеры переключаются одновременно (по счетному импульсу) и лишь потом происходит перенос в цепи логических элементов. Значит, для съема информации дополнительного времени не требуется – можно использовать время TПЕР
. В этом смысле быстродействие синхронного счетчика выше, чем асинхронного.
4. Счетчики и делители с коэффициентомпересчета, отличным от 2n
Большое распространение получили счетчики и делители с Kn
≠ 2n
. Так, в цифровых индикаторных устройствах доминируют двоично-десятичные счетчики (Kn
= 10).
Принцип построения счетчиков с Kn
≠ 2n
сводится к следующему. Берут такое число nтриггеров, чтобы выполнялось условие
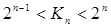 . .
Затем схемным путем исключают 2n
-Kn
, избыточных состояний. Чаще всего исключают старшие состояния, реже – младшие или промежуточные. Делается это либо с помощью дешифратора определенного состояния, который своим выходным сигналом принудительно устанавливает счетчик в исходное состояние, либо с помощью обратных связей между триггерами.
На рис. 5 приведен пример декадного (двоично-десятичного) счетчика с исключением старших избыточных состояний.
Начальное состояние у него нулевое: A0
{0000}. При поступлении входных импульсов счет идет как в обычном двоичном счетчике. Как только устанавливается состояние A10
{1010}, на выходе элемента И, играющего роль дешифратора, вырабатывается сигнал y=Q1
Q3
=1, и счетчик принудительно переводится в начальное состояние A0
.
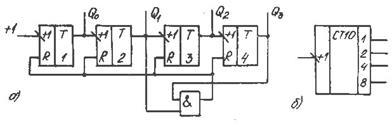
Рис. 5
Примером использования обратных связей для исключения избыточных состояний может служить ИС 133ИЕ2 (рис. 6,а). Она содержит T-триггер D1 и двоично-пятеричный счетчик на триггерах D2, D3, D4. Благодаря обратной связи с выхода Q3
триггера D4 на вход Jтриггера D2, а также обратной связи в самом триггере D4 (с выхода Q3
на вход К), обеспечивается соответственно блокировка действия пятого счетного импульса на триггер D2 и установка триггера D4 пятым импульсом в нулевое состояние (рис. 6,б). Таким образом, после пятого импульса получается A0
{000}.
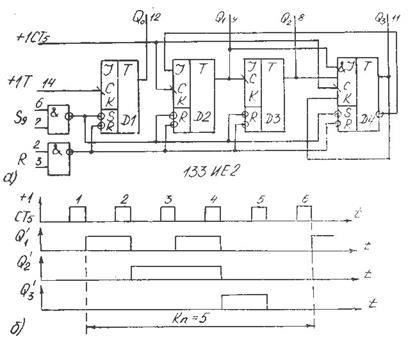
Рис. 6
Если выход Q0
триггера D1 соединить со входом +1СТ, а счетные импульсы подавать на вход +1Т, то счетчик становится двоично-десятичным с Kn
= 10.
Как отмечалось ранее, принцип построения делителей во многом аналогичен принципу построения счетчиков. Они имеют, как правило, один выход, на котором за интервал пересчета появляется импульсов в коэффициент деления раз меньше, чем поступают на вход
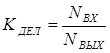 . .
Выделяются эти импульсы с помощью дешифратора состояний.
Менять коэффициент KДЕЛ
в делителях можно так же, как счетчиках с Kn
≠ 2n
, т.е. путем исключения различного числа избыточных состояний, но и программно – с помощью внешних управляющих сигналов. Такой способ реализован, например, в ИС 564ИЕ15. Она позволяет получать КДЕЛ
= 3...21327 с шагом единица.
Нашел распространение также способ, при котором коэффициент пересчета счетчика, составляющего основу делителя, не меняется, а производится выбор дешифраторов, настроенных на выделение различных состояний счетчика. Данный способ построения делителей иллюстрируется на примере ИС 133ИЕ8 (рис. 7).

Рис. 7
Делитель состоит из шестиразрядного двоичного счетчика с параллельным переносом, дешифраторов состояний на ЛЭ1…ЛЭ6, выходы которых объединены в один выход yэлементом ИЛИ-НЕ (ЛЭ7), а также дешифратора-формирователя сигнала переноса CRи вспомогательных логических элементов. Каждый дешифратор включается в работу при подаче на него управляющего сигнала K’i
= 1.
Дешифраторы настроены на выделение неодинаковых состояний. Например, дешифратор на ЛЭ1 выделяет состояния 0, 2, 4 и т.д. через 2, на ЛЭ2 - 1, 5, 9 и т. д. через 4 на ЛЭ3 – 3, 11, 19 и т.д. через 8. Поэтому сигналы (импульсы) на выходах дешифраторов во времени не совпадают, и на общем выходе yполучается их сумма.
Таким образом, за один цикл работы, который содержит 26
= 64 входных импульсов, число импульсов на выходе yбудет меньше и определяется числом
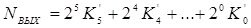
в соответствии с кодовой комбинацией на входах K0
…K5
. Коэффициент деления
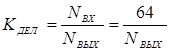 . .
Если только один из сигналов K’i
= 1, то NВЫХ
= 2i
и коэффициент деления – целое число. В остальных случаях коэффициент деления – число дробное.
Следует обратить внимание на то, что если входная последовательность импульсов периодическая, то выходная последовательность будет периодической только тогда, когда коэффициент деления - целое число, в других случаях выходные импульсы распределены во времени неравномерно.
С целью увеличения диапазона перестройки коэффициента деления, микросхемы соединяют последовательно. Сигналы переноса играют роль входных по отношению к последующим микросхемам.
|