Міністерство транспорту та зв’язку України
Одеська національна академія зв’язку ім. О.С. Попова
Кафедра інформатизації та управління
КУРСОВА РОБОТА
з дисципліни “Теорія автоматичного керування ”
Виконала:
студентка 3-го курсу
групи КТ-3.09
Лузіна Т.А.
варіант №14
Керівники:
Кушнiр I. C.
Харабет О. М.
Одеса 2010
Зміст
1. Визначення перехідної функції об’єкта керування
2. Побудова кривої розгону об’єкту
3. Обчислення і побудова комплексно-частотної характеристики (КЧХ) об’єкта
4. Побудова межі cтiйкостi АСР
5. Обчислення оптимальних параметрів регулятора
6. Побудова КЧХ розімкнутої автоматичної системи регулювання.
Визначення запасу сталості за модулем і фазою
7. Вибір налаштувань ПІ-регулятора за методикою Л.І. Кона
8. Вибір налаштувань ПІ - регулятора за методикою А.П. Копеловича
Висновки
Список літератури
Вихідні дані:
KM
=3.2 од.
T1
=45 c
T2
=11 c
t = 7 c
ΔN=50 од. збурення
m=0,37 кореневий показник коливальності.
Побудова кривої розгону.
Математичний опис діючого об’єкта керування в АСР у вигляді диференційного рівняння:
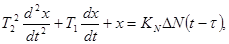
Розв’язання цього рівняння зручно виконувати зі застосовуванням способу операторного перетворення Лапласа. Відповідно до цього передатна функція об’єкта по каналу збурення:
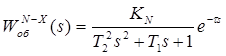
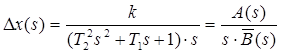
Для переходу від зображення вихідної функції до її оригіналу ∆x (t) можна застосовувати метод О. Хевісайда. Формула Хевісайда:
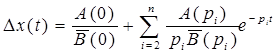
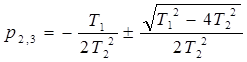
Якщо корені характеристичного рівняння p2
, p3
- речовинні і уявні, розв’язання:
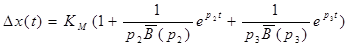
Km: =3.2
τ: =7
T1: =45 T2: =11 m: =0.37 ΔN: =50
P2: = - 0.024 P3: = - 0.348
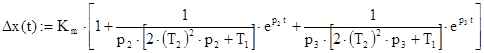
Крива розгону ПІ - регулятора наведена на рис.1:
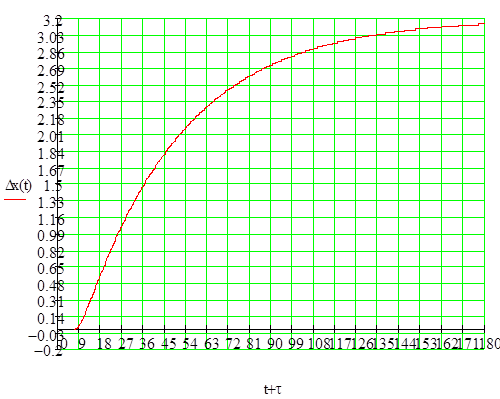
Рисунок 1. Крива розгону на виході об’єкта.
Перевід задачі в частотну область здійснюється шляхом формальної заміни повною комплексною незалежною змінною s її чисто комплексною частиною ωj:
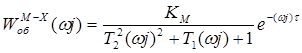
Дійсну і уявну частини КЧХ об’єкта по каналу регулювання можна визначити формулами:
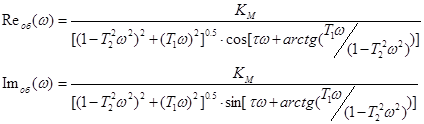
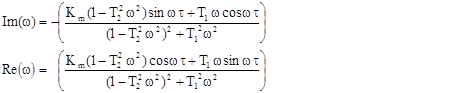
Для побудови КЧХ об’єкта без запізнення використовувались формули
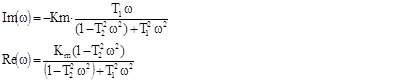
На рис.2. наведені КЧХ об’єкту без запізнення та з запізненням.
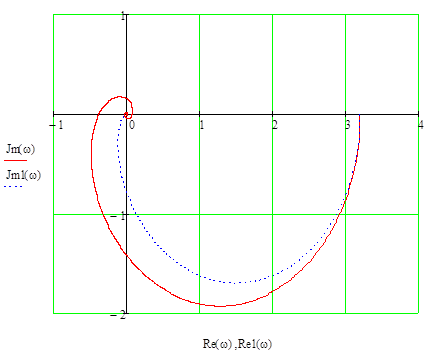
Рисунок 2. - КЧХ об’єкту:
a) з запізненням (суцільний); б) без запізнення (пунктирний).
Вирази для визначення настройок, відповідних межі сталості АСР:
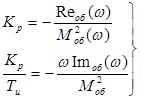
Кожному значенню колової частоти відповідає пара значень параметрів настройок Кр
і Кр/
Тu
. Для даної АСР межа області сталості повинна розташовуватися у верхній площині параметрів.
Після побудови межі стiйкості визначаємо значення точки максимуму:
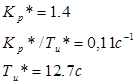
Межа стiйкості наведена на рис.3.
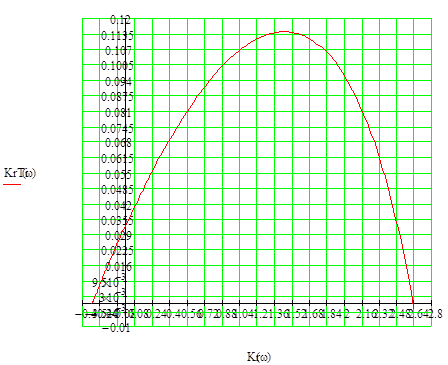
 Рисунок 3. Побудова межі стiйкості АСР.
Визначенню підлягають налаштування, що найкраще забезпечують заданий ступінь коливальності для ПП або ступінь загасання ПП:
 
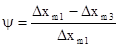
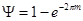
Виконавши формальну заміну s на  одержимо
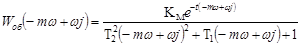
Для побудови розширеної КЧХ об’єкту: за дійсною та фіктивною частинами.
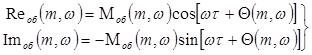
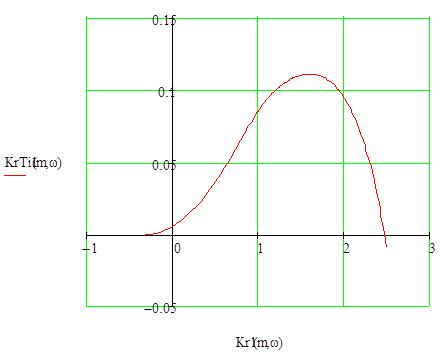
Рисунок 4. - РКЧХ об’єкту при m=0,37
З графіку ми бачимо, що оптимальними настройками для даної АСР буде Кр=1.6;
Кр/Тu=0.12;
Тu=13.3с.
Як і раніше, дана КЧХ - Wpc ( ) вираховується і будується за дійсною і фіктивною складовими.
Або з урахуванням КЧХ ПІ-регулятора.
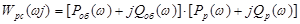
Звідси отримуємо:
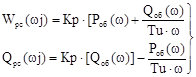
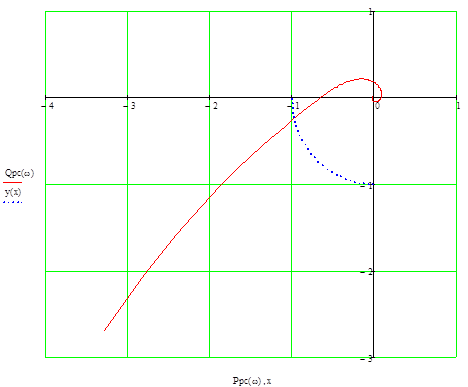
Рисунок 5- Побудова КЧХ розімкненої системи АСР
З цього графіку знайдені параметри С та g - запаси сталості за модулем та фазою відповідно:
С=0.3; γ = o
.
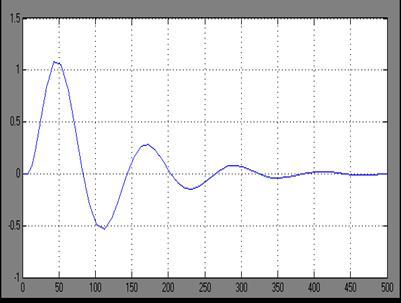
Рисунок 6 - Графік перехідного процесу регулювання в АСР (налаштування регулятора знайденi за методом РКЧХ).
З рисунку 5 знайдемо:
ΔХ1=1.1;
ΔХ3=0.25;
Tp=400c;
Ψ=0.77;
γ= 0
;
C=0.3;
Всi розрахунки зведенi до таблицi 1.
Відокремлюваною особливістю методики є апроксимація складного об’єкта ланцюгом простих інерційних ланок 1-го порядку.
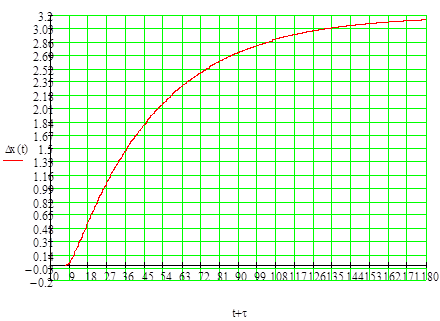
Рисунок 7. Обробка кривої розгону об’єкту регулювання
Та=56с
τ =7с
а= τ / Та =0.12
m=0.37
q=2
Знайдемо із показників с=2.12 і к= 1.09 значення Кр і Тu:
Тu=7*2.12=14.84с, Кр=1.09/3.2=0.34.
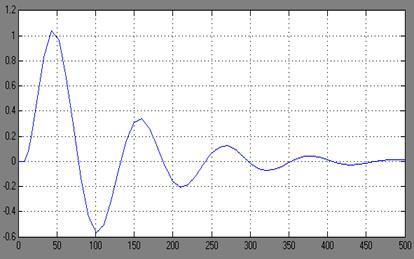
Рисунок 8. - Графік перехідного процесу регулювання в АСР (налаштування регулятора знайденi за методом Кона)
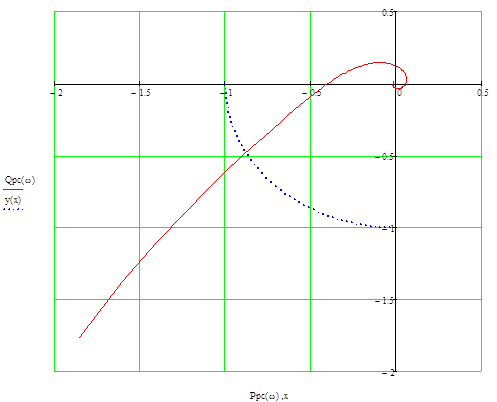
Рисунок 9- Побудова КЧХ розімкненої системи АСР
З рисунку 8 знайдемо:
ΔХ1=1.1;
ΔХ3=0.35;
Tp=400c;
Ψ=0.68;
γ= 0
;
C=0.6
m=0.18
Всi розрахунки зведенi до таблицi 1.
Методика Копеловича дає можливість задовольнити вимогу до якості ПП регулювання шляхом попереднього вибору типу регулятора. В практиці часто бувають обмежені максимальні динамічні відхилення регульованих величин від заданого значення 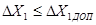 і час регулювання tP
≤ tPдоп
З нормограмми для вибору налаштувань ПI та- регулятора з рис.3 обираємо свої параметри:
t/Тu
=0.12;
Знайдемо, що
Kp=2.18;
Тu
=24.5c.
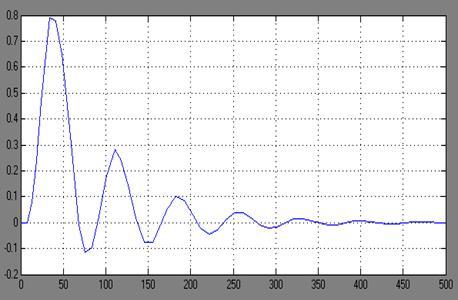
Рисунок 10. - Графік перехідного процесу регулювання в АСР (налаштування регулятора знайденi за методом Копеловича)
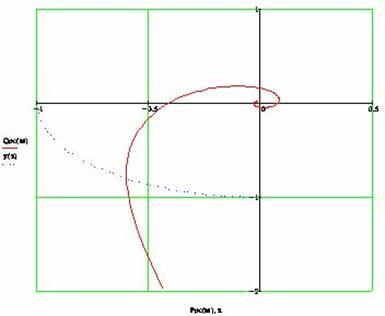
Рисунок 11 - Побудова КЧХ розімкненої системи АСР
З рисунку 10 знайдемо:
ΔХ1 = 0.8;
ΔХ3 = 0.3;
Tp = 400c;
Ψ = 0.63;
γ =;
C = 0.6;
m = 0.16;
Всi розрахунки зведенi до таблицi 1.
Таблиця 1. - Зведена таблиця основних результатів курсової роботи
Спосіб
визначення настройок
|
Кр |
Тu |
m |
ΔХ1 |
ΔХ3 |
C |
γ |
Ψ |
Tp |
| Метод розширеної КЧХ |
1.6 |
13.3 |
0.37 |
1.1 |
0.25 |
0.3
|
0.77 |
400 |
Метод Кона
|
0.34 |
14.84 |
0.18 |
1.1 |
0.35 |
0.6 |
0.91 |
400 |
| Метод Копеловича |
2.18 |
24.5 |
0.16 |
0.8 |
0.3 |
0.6 |
0.63 |
450 |
При виконанні курсової роботи були закріплені одержанні знання з теорії лінійних одноконтурних автоматичних систем регулювання.
За результатами обчислення координат була побудована крива розгону об’єкта; обчислені координати і побудована КЧХ обיєкта з запізненням та без запізнення; побудована межа тривалості АСР в координатах КР -
КР
/Tи
; були визначені оптимальні настройки ПІ - регулятора різними методами; побудована КЧХ розімкненої АСР.
Порівнюючи налаштування, отримані за методиками Кона, Копеловича, з налаштуванням, отриманими з точки максимуму, зробили висновок:
метод Копеловича не досить точний, тому що в ньому застосовуються номограми, по яким визначалися налаштування, допускають допускають велику похибку (в тому числі через те, що в них використовується логарифмічна шкала). Перехідний процес при настройках, вибраних по методикам Кона, дає найбільш прийнятний результат ніж інші. Але ні один з методів не являється досить добрим, у кожного є свої переваги й недоліки, тому їх потрібно обирати в конкретній ситуації вже інженеру-наладчику АСР самостійно.
1. Методические указания и таблицы для выбора настроек ПИ- и П - регуляторов в одноконтурных системах регулирования тепловых объектов с запаздыванием. / Л.И. Кон. - Одесса: ОПИ, 1975
2. Климовицкий М.Д., Копелович А.П. Автоматический контроль и регулирование в чёрной металлургии: Справочник. - М.: Металлургия, 1967. - с.372-378; 417-425.
3. Попович М.Г., Ковальчук О.В. Теорія автоматичного керування: Підручник для вищих технічних закладів освіти. - К.: Либідь, 1997.
|
