Министерство Российской Федерации
Томский политехнический университет
__________________________________________________________________
Е.Л. Собакин
ЦИФРОВАЯ СХЕМОТЕХНИКА
Часть
I
Учебное пособие
Томск 2002
УДК 681.325.6
Собакин Е.Л. Цифровая схемотехника
. Учеб. пособие. Ч.I. - Томск: Изд. ТПУ, 2002. - 160с.
В пособии изложены основные вопросы курса лекций для студентов специальности 210100 - Управление и информатика в технических системах. Пособие подготовлено на кафедре автоматики и компьютерных систем ТПУ, соответствует учебной программе дисциплины и предназначено для студентов института дистанционного образования.
Печатается по постановлению Редакционно-издательского Совета Томского политехнического университета
Рецензенты:
В.М. Дмитриев - профессор, доктор технических наук, заведующий кафедрой теоретических основ электротехники Томского университета систем управления и радиоэлектроники;
С.И. Королёв - директор ТОО НПО «Спецтехаудитсервис»,
кандидат технических наук, старший научный сотрудник.
Темплан 2002
ã Томский политехнический университет, 2002
Введение
Данное учебное пособие предназначено для студентов высших учебных заведений, обучающихся по специальности 210100 - "Информатика и управление в технических системах". Оно составлено на основе курса лекций, прочитанных автором в Томском политехническом университете в течение ряда лет, и посвящено систематическому изложению методов формализованного построения устройств цифровой техники на микросхемах широкого применения.
В пособии содержатся краткие сведения по интегральным микросхемам, достаточные для определения основных технических показателей и характеристик цифровых устройств, для уяснения их принципа действия и выполнения технических расчётов.
Дисциплину "Цифровая схемотехника" следует рассматривать как продолжение курса «Электроника», который студенты должны освоить предварительно, так как требуются знания элементной базы аналоговых электронных устройств.
Большинство современных систем автоматики, вычислительные системы, системы передачи и обработки информации выполняются на устройствах цифровой техники либо полностью, либо частично. Поэтому знание принципов применения цифровых устройств и построения на их основе систем различного назначения имеет актуальное значение и большую практическую ценность как в инженерной деятельности, так и при исследованиях методологического характера.
Материал пособия условно можно разделить на три части: 1) Основы микроэлектроники; 2) Комбинационные устройства цифровой техники; 3) Последовательностные логические устройства цифровой техники.
Приступая к освоению курса, следует изучать материал в порядке перечисления указанных частей, так как последующий материал основан на знании предыдущего, и изменение последовательности может привести к затруднениям в его усвоении. Это усугубляется ещё и тем, что в иных учебных пособиях и специальной технической литературе используются различные термины и понятия для пояснения одних и тех же явлений, процессов, выполняемых преобразований и т.д. Различие же в используемых понятиях или их некорректность ведёт к непониманию сущности излагаемого материала и, как следствие, возникновению трудностей в его усвоении.
Первые два из указанных разделов вошли в первую часть настоящего пособия (Ч1). Третьему разделу посвящено отдельное пособие.
В1
. Применение цифровых устройств
В настоящее время, в связи с созданием и широким внедрением в инженерную практику микропроцессорных устройств и систем, не ослабевает и вновь стимулируется интерес к цифровым методам обработки и передачи информации. Названные методы, в свою очередь, придают системам ряд положительных свойств и качеств. Повышается верность передаваемой информации, достигается высокая скорость и производительность систем обработки информации, обеспечивается приемлемая их стоимость, высокая надёжность, малое потребление энергии и т. д.
Решаемые этими системами задачи весьма разнообразны и предопределяют функции устройств, образующих конкретную систему. Поэтому устройства и их функции целесообразно рассматривать именно в свете тех задач, которые решаются системами и, в частности, тех подзадач, которые выполняются отдельными устройствами либо блоками.
Основными типовыми задачами
, возникающими при автоматическом или автоматизированном управлении и контроле производственными или иными процессами, являются:
* сбор
информации (её получение);
·преобразование
информации (масштабирование, нормализация, фильтрация, кодирование и т. д.);
* передача-приём
информации;
* обработка и использование
информации;
* хранение
информации.
В зависимости от целевого назначения и основных функций различают:
Чтобы уяснить взаимосвязь указанных задач, место и роль электронных цифровых устройств, используемых в названных системах, рассмотрим обобщённые структурные схемы этих систем и функциональное назначение их составных частей.
В1.1. Системы автоматического управления
Управлять
- означает знать состояние (положение) управляемого объекта и в соответствии с заданным алгоритмом (алгоритмом управления
) воздействовать на объект, стремясь устранить возникающие отклонения.
Поэтому управление в общем случае связано с выполнением следующих действий:
* получение информации о состоянии объекта;
* сопоставление полученной информации с заданной информацией о состоянии объекта;
* формирование управляющих сигналов (воздействий);
* воздействие на объект с целью приведения его в требуемое состояние.
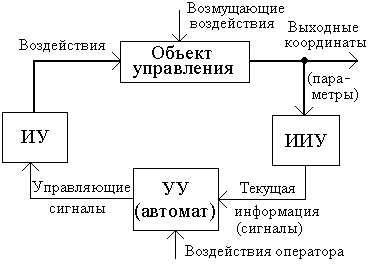
В соответствии с перечисленными действиями в систему автоматического управления (САУ) в общем случае должны входить информационно-измерительное устройство, устройство управления и исполнительное устройство (рис. В1).
 Информационно-измерительное устройство
(ИИУ) получает информацию об объекте управления (ОУ) и предварительно её обрабатывает. Получение информации заключается в формировании первичных сигналов, значения которых пропорциональны значениям параметров, характеризующих состояние ОУ. Под объектом можно понимать как отдельную производственную установку, так и производственный процесс в целом. А под параметрами - "выходные координаты" объекта. Это могут быть, например, значения температуры, давления, расхода материалов или энергии и тому подобное. Поскольку большинство таких координат-параметров представлены в аналоговой форме и характеризуются бесконечным множеством значений, то сигналы должны быть нормализованы по своим параметрам, масштабированы и иметь унифицированную форму. Информационно-измерительное устройство
(ИИУ) получает информацию об объекте управления (ОУ) и предварительно её обрабатывает. Получение информации заключается в формировании первичных сигналов, значения которых пропорциональны значениям параметров, характеризующих состояние ОУ. Под объектом можно понимать как отдельную производственную установку, так и производственный процесс в целом. А под параметрами - "выходные координаты" объекта. Это могут быть, например, значения температуры, давления, расхода материалов или энергии и тому подобное. Поскольку большинство таких координат-параметров представлены в аналоговой форме и характеризуются бесконечным множеством значений, то сигналы должны быть нормализованы по своим параметрам, масштабированы и иметь унифицированную форму.
Поэтому в ИИУ должны быть первичные измерительные преобразователи и датчики, аналого-цифровые преобразователи и другие функциональные узлы, с помощью которых выполняются следующие преобразования:
* значений физических величин в унифицированные аналоговые сигналы постоянного или переменного тока;
· масштабирование или нормирование сигналов по уровню и форме;
· преобразование аналоговых сигналов в дискретные (цифровые) сигналы;
кодирование сигналов и некоторые другие преобразования.
Сигналы о текущих значениях координат поступают на устройство управления
(УУ). В функции этого устройства входит сравнение текущих значений с заданными значениями координат и формирование по результатам сравнения сигналов управления (управляющих сигналов). Заданные значения могут вводиться человеком-оператором либо автоматически программно. В первом случае в качестве УУ может использоваться автоматический регулятор или несколько автоматических регуляторов, уставки которым определяет и задаёт человек. Во втором случае УУ представляет собой программный автомат мини- либо микроЭВМ и роль человека-оператора сводится к вводу программы и первоначальному пуску системы.
Для выполнения указанных функций от УУ требуется выполнять арифметические и логические операции по вычислению значений и сравнению сигналов, кратковременному и долговременному запоминанию (хранению) сигналов и формированию управляющих унифицированных сигналов. Последние содержат информацию, на основе которой далее формируются воздействия на объект управления (управляющие воздействия), приводящие его в требуемое состояние.
Непосредственно воздействия требуемой физической природы формирует исполнительное устройство
(ИУ). Оно преобразует управляющие сигналы, например, в виде напряжения постоянного или импульсного тока, в скорость вращения исполнительного двигателя, в механическое перемещение клапана на паропроводе и так далее. Для выполнения этих преобразований потребуются: преобразователи цифровых сигналов в аналоговые; преобразователи электрических сигналов - в неэлектрические; усилительные устройства и т.д. При этом в качестве промежуточных могут потребоваться преобразователи кодов цифровых сигналов, либо формы представления сигналов. Например, кодов двоичных чисел в пропорциональное количество импульсов, однофазных сигналов в многофазные, используемые для управления шаговыми двигателями и т. д.
Под действием возмущающих воздействий объект выходит из нормального состояния (режима), а САУ возвращает его в требуемый (нормальный) режим работы. Процесс управления протекает в реальном масштабе времени, то есть со скоростью, определяемой характером физических процессов. Если управляющие воздействия запаздывают во времени либо чрезмерны, то может возникнуть неустойчивый режим работы системы, при котором координаты объекта могут принять недопустимые значения и либо сам объект, либо отдельные устройства системы выйдут из строя - возникнет аварийный режим. Поэтому в теории САУ основными
являются проблемы обеспечения устойчивости и точности управления.
Большинство из перечисленных преобразований могут быть выполнены с помощью цифровых микроэлектронных устройств. Полностью цифровым является УУ, когда оно строится на основе управляющих микроЭВМ либо на цифровых микросхемах.
На цифровых микросхемах выполняются цифровые датчики физических величин, а так же частично аналого-цифровые и цифро-аналоговые преобразователи сигналов.
В1.2. Системы передачи информации (СПИ)
При увеличении расстояния между ИИУ и УУ (рис. В1), а также между УУ и ИУ, возникает задача передачи информации
. Необходимость передачи информации на значительные расстояния возникает не только в пространственно развитых системах автоматического управления и контроля, но и в системах
других видов связи
(телеграфной, телефонной, телефаксной и др.). Кроме того, необходимость передачи информации возникает в вычислительных системах, системах передачи данных, телемеханических системах и т. д. Эта задача осложняется тем, что в процессе передачи по линиям связи
искажаются параметры сигналов
и это, в свою очередь, может привести к искажению информации - к снижению её верности (вероятности правильного её приёма). Искажение же сигналов обусловлено действием помех
, возникающих в линиях связи
. Помехи, как правило, имеют случайный характер и по своим параметрам могут и не отличаться от параметров сигналов. Поэтому они "способны" искажать сигналы и даже "воспроизводить" информацию -трансформировать передаваемое сообщение
. Последнее самое нежелательное событие в передаче информации.
Чтобы обеспечить высокую верность и максимальную скорость (эффективность
) передачи информации, требуются дополнительные преобразования сигналов и специальные методы их передачи.
К таким преобразованиям относятся кодирование
и обратная процедура -декодирование информации
(и сигналов). Кодирование
-
есть процедура преобразования сообщения в сигнал
. При этом преобразования осуществляются по определённым правилам,
совокупность которых называется кодом
.
Кодирование информации выполняется на передающей стороне, а декодирование на приёмной. Различают помехоустойчивое кодирование и эффективное
. Цель помехоустойчивого
кодирования
-
построить (сформировать) сигнал, менее подверженный действию помех, придать ему такую структуру, чтобы возникшие в процессе передачи ошибки на приёмной стороне можно было бы обнаружить либо исправить
. И, тем самым, обеспечить высокую верность передачи.
Цель эффективного
кодирования
-
обеспечить максимальную скорость передачи информации, так как её ценность во многом определяется, насколько своевременно она получена
. Согласно этому требованию закодированное сообщение должно нести требуемое количество информации и, в то же самое время, иметь минимальную длину, чтобы на передачу потребовалось минимум времени.
Передача сигналов (и информации) осуществляется по каналам связи
. Канал связи
-это тракт (путь) независимой передачи сигналов от источника к соответствующему приёмнику (получателю) информации.
Каналы связи образуются техническими средствами - каналообразующей аппаратурой - и так же, как и линии связи подвержены влиянию помех.
Одной из основных решаемых в СПИ задач является задача создания требуемого числа каналов связи. Эффективность и помехоустойчивость передачи во многом определяется используемыми каналами связи. Под помехоустойчивостью понимают способность системы
(сигнала, кода) правильно выполнять свои функции в условиях действия помех
.
Обычно одну и ту же систему можно использовать для передачи информации от многих источников к соответствующему числу приёмников (получателей). Поэтому образование требуемого числа каналов с необходимой помехозащищённостью возлагается на устройство связи. При этом в устройстве связи могут выполняться следующие преобразования: модуляция и демодуляция
сигналов; усиление передаваемых в линию и принимаемых из линии
связи сигналов; ограничение по уровню и частотному спектру
сигналов и некоторые другие.
В зависимости от области использования (применения) СПИ возникает необходимость в дополнительных преобразованиях таких, как преобразование формы сигналов, их физической природы, нормирование параметров поступающих извне сигналов и сигналов, выдаваемых системой на внешние устройства; временное хранение передаваемых в канал связи и выдаваемых системой сигналов.
Перечисленные преобразования предопределяют функциональный состав передающей и приёмной аппаратуры систем передачи информации (рис.В2).
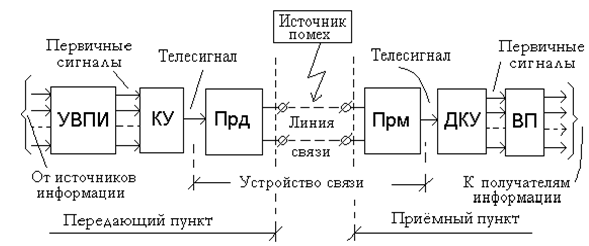 |
Как видно по схеме, передача осуществляется в одном направлении - слева направо. Устройство ввода и первичного преобразования информации (УВПИ) преобразует поступающие от источников информации сигналы в унифицированные «первичные» сигналы, которые невозможно непосредственно передать на большие расстояния. Обычно, эти унифицированные сигналы представляют собой напряжение постоянного тока с фиксированными значениями по уровню. В блоке УВПИ первичные сигналы сохраняются на время передачи (в буферном запоминающем устройстве), после чего стираются из памяти. Кодирующее устройство (КУ) преобразует первичные сигналы в кодированные сигналы, имеющие определённую структуру и формат, допускающие возможность передачи их (сигналов) на большие расстояния («телесигналы»). Как правило, это устройство является комбинационным, хотя в ряде случаев может быть выполнено и последовательностным (многотактным). Здесь реализуются логические и арифметические операции процедур кодирования.
Основным назначением устройства связи (рис. В2) является создание или организация каналов связи
на предоставленной линии связи. Линия связи
- это материальная среда между передатчиком (Прд) и приёмником (Прм) системы. На рисунке условно показана двухпроводная линия электрической связи. Однако могут использоваться радиолинии и волоконно-оптические линии связи и другие. В зависимости от типа линии в Прд и Прм выполняются различные преобразования сигналов с целью согласования их параметров и характеристик с параметрами и характеристиками линии связи и преобразования, направленные на повышение помехоустойчивости
сигналов.
На приёмной стороне принятые из линии связи кодированные сигналы вновь преобразуются декодирующим устройством (ДКУ) в первичные сигналы. При этом в принятых сигналах процедурами декодирования обнаруживаются и могут исправляться ошибки и, тем самым, обеспечивается требуемая верность передачи информации. А выходные преобразователи
(ВП) преобразуют эти первичные сигналы в форму и вид (физическую природу), которую могут воспринимать получатели информации.
Следует отметить, что большинство функциональных «узлов» и «блоков», показанных на рис.В2, могут быть выполнены на цифровых микросхемах. Поэтому системы передачи информации, как правило, являются цифровыми.
В1.3. Системы обработки информации
(вычислительные системы)
Перечисленные выше типовые задачи могут быть решены и формализованы математическими и логическими методами. В свою очередь названные методы оперируют простейшими операциями (арифметическими или логическими), выполнением которых над некоторыми «исходными данными» получается новый результат, ранее неизвестный. Эта общность методов решения разнообразных задач по обработке информации позволила создать отдельный класс устройств и систем, целевым назначением которых (первоначально) была автоматизация вычислительных процедур - электронные вычислительные машины (ЭВМ). На современном этапе развития вычислительной техники ЭВМ «превратились» в компьютеры, на основе которых строятся современные компьютерные системы обработки и передачи информации. Обобщённая структурная схема некоторой вычислительной системы приведена на рис.В3.
 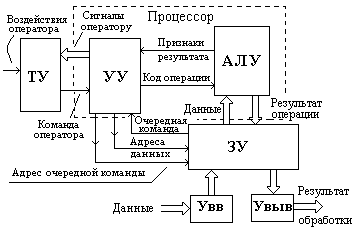
Обрабатываемые данные предварительно через устройство ввода
Увв
поступают на запоминающее устройство
ЗУ
, где сохраняются на всё время обработки. В этом же ЗУ хранится и программа обработки поступающей информации.
Программа работы системы так же, как и «данные», хранятся в запоминающем устройстве в виде многоразрядных двоичных чисел, записанных в ячейки ЗУ по определённым адресам (адресам ячеек памяти). Двоичные числа, совокупность которых отображает программу обработки данных, структурированы на определённое число частей, каждая из которых имеет определённое назначение. В простейшем случае имеются следующие части: 1) код операции, которую надо выполнить с двумя двоичными числами, отображающими значения «данных» и называемыми «операндами»; 2) адрес первого операнда; 3) адрес второго операнда. Совокупность этих частей образует «команду».
Работа ЭВМ заключается в последовательном выполнении команд, заданных программой. Координирует работу всех блоков во времени и управляет ими управляющее устройство
УУ
. А непосредственно логические и арифметические операции (действия) над операндами выполняет арифметико-логическое устройство
АЛУ
, которое по сигналу от УУ «код операции» каждый раз настраивается на выполнение конкретной операции.
Устройство управления расшифровывает поступившую от ЗУ команду (рис. В3 «очередная команда»), код операции направляет на АЛУ и оно готовится к выполнению соответствующей операции. Затем формирует сигналы выборки из ЗУ операндов (см. сигнал «Адреса данных») и определяет адрес очередной команды, которую следует выполнить на следующем такте работы ЭВМ («Адрес очередной команды»). По сигналам от УУ из ЗУ считываются операнды, и АЛУ выполняет необходимые действия. При этом образуется промежуточный результат («Результат операции»), который также сохраняет ЗУ. В зависимости от результата выполнения операции может появиться необходимость изменения последовательности выполнения команд, либо прекратить обработку данных, либо вывести оператору сообщения об ошибках. Для этой цели с АЛУ на УУ поступает сигнал «Признак результата». Процесс обработки введённых данных (информации) продолжается до тех пор, пока не будет извлечена команда «Конец вычислений», либо оператор по своему усмотрению не остановит процесс обработки данных.
Полученный результат обработки также хранится в ЗУ и может быть выведен через устройство вывода
Увыв
по окончании процесса обработки либо в ходе процесса, если это предусмотрено программой.
Для «общения» оператора с ЭВМ предусматриваются терминальные устройства
ТУ
, предназначенные для ввода оператором команд и других сообщений и для вывода оператору «сообщений» со стороны ЭВМ.
На рис.В3 не показаны связи управляющего устройства, обеспечивающие синхронизацию работы всех составных частей ЭВМ. Широкими стрелками отображается возможность параллельной передачи данных (одновременной передачи всех разрядов многоразрядных двоичных чисел).
Практически все показанные на рис.В3 блоки (кроме терминальных устройств) могут быть полностью выполнены только на цифровых интегральных микросхемах (ИМС). В частности, УУ, АЛУ и часть ЗУ (регистровая память - СОЗУ) могут быть выполнены в виде одной ИМС большой степени интеграции. Названная совокупность блоков образует микропроцессор
- центральный процессор ЭВМ, выполненный средствами интегральной технологии на одном кристалле полупроводника.
Устройства ввода и вывода данных, как правило, состоят из буферных запоминающих регистров, служащих для временного хранения, соответственно, вводимых и выводимых данных и для согласования системы с внешними устройствами.
Запоминающее устройство (ЗУ) обычно разделяют на две части: оперативное ЗУ (ОЗУ) и постоянное ЗУ. Первое служит для хранения промежуточных результатов вычислений, его «содержимое» постоянно изменяется в процессе обработки данных. ОЗУ работает в режимах «считывания» и «записи» данных. А второе, постоянное ЗУ (ПЗУ), служит для хранения стандартных подпрограмм и некоторых системных (служебных) подпрограмм, управляющих процессами включения и выключения ЭВМ. Как правило, ПЗУ выполняется на программируемых пользователем ИМС ПЗУ (ППЗУ), либо заранее запрограммированных на заводах-изготовителях ИМС ПЗУ, либо перепрограммируемых пользователем ПЗУ (РеПЗУ). Обычно это энергонезависимые запоминающие устройства, в которых записанная информация не «разрушается» даже при их отключении от источника питания.
В состав АЛУ входят одноимённого названия ИМС, выполняющие логические и арифметические операции с двоичными числами, логические элементы и ряд других функциональных узлов, служащих для сравнения чисел - цифровые компараторы, для увеличения быстродействия выполняемых арифметических операций, например «блоки ускоренного переноса» и т.д.
В состав УУ входят таймерные устройства, задающие тактовую частоту работы системы и, в конечном итоге, определяющие её производительность, дешифраторы кодов команд, программируемые логические матрицы, регистры, блоки микропрограммного управления, а также «порты» ввода-вывода.
Все перечисленные функциональные узлы выполняются в виде интегральных цифровых устройств.
Основными проблемами
вычислительных систем являются, во-первых, повышение их производительности
(быстродействия). И, во-вторых, обеспечение работы систем в реальном «масштабе» времени
.
Первая проблема носит общесистемный характер и решается путём применения новой элементной базы и специальных методов обработки информации.
Вторая проблема возникает при использовании вычислительных систем для управления производственными процессами и заключается в том, что скорости протекания производственных и вычислительных процессов должны быть согласованы. Действительно, функционирование вычислительной системы (ВС) происходит в так называемом «машинном» времени, когда за единицу времени принимается некоторый фиксированный и неделимый интервал времени, называемый «тактом работы» ЭВМ или компьютера, тогда как реальные физические процессы, например технологические процессы, протекают в реальном времени, измеряемом в секундах, долях секунды, в часах и т.д. Чтобы применение ЭВМ стало возможным, необходимо скорость обработки информации сделать не менее скорости протекания реальных физических процессов. Решение этой проблемы достигается организацией специальных методов обмена информацией (данными) управляющей ЭВМ с периферийными устройствами и применением специальных, так называемых интерфейсных схем и устройств
. В функции интерфейсных схем входит:
· определение адреса внешнего устройства, требующего обмена информацией с процессором либо с запоминающим устройством системы;
· формирование сигналов прерывания работы процессора ВС и инициализация перехода к программе обслуживания объекта, запросившего прерывание. Это осуществляется по специальной системе приоритетов
;
· реализация очередей на обслуживание внешних устройств;
· согласование по параметрам и времени сигналов обмена и т.д.
Благодаря современным достижениям в области интегральной технологии в изготовлении микроэлектронных устройств, созданию микроЭВМ и компьютеров, характеризующихся малыми габаритами, малым потреблением энергии и приемлемой стоимостью, стало возможным их применение в составе систем самого различного назначения. При этом эти системы приобретают новые качества и становятся многофункциональными с возможностью гибкого перехода от одного режима работы к другому путём простого изменения конфигурации систем. В свою очередь, эти достоинства открывают новые перспективы в применении компьютерных систем в самых разнообразных областях человеческой деятельности: в науке, в медицине, в образовании и подготовке кадров и тем более в технике.
Например, телефонная связь традиционно осуществлялась аналоговыми устройствами, когда человеческая речь передавалась (по проводам) сигналами в виде переменных токов звуковых частот. Теперь же наметился интенсивный переход к цифровой телефонной связи, при которой аналоговые сигналы (от микрофона) преобразуются в цифровые, передаваемые на большие расстояния без существенных искажений. На приёмной стороне эти цифровые сигналы вновь преобразуются в аналоговые и доводятся до телефона. Переход к цифровой связи позволяет повысить качество передачи речи, кроме того, телефонную сеть можно использовать для других услуг: охранной сигнализации; пожарной сигнализации; для «конференцсвязи» нескольких абонентов и так далее.
В2. Сравнительная оценка цифровых и аналоговых устройств
микроэлектронной техники
Решая вопрос о построении или проектировании, какого либо устройства, следует предварительно принять решение о направлении проектирования, - каким будет устройство? -Аналоговым
либо дискретным
(цифровым)? В свою очередь, это решение можно принять, зная достоинства и недостатки тех и других устройств. Предварительно дадим определения понятиям «аналоговые» и «цифровые» устройства.
Аналоговым
называется такое устройство
, у которого все сигналы входные, выходные и промежуточные (внутренние) являются непрерывными, описываются непрерывными математическими функциями. Эти сигналы характеризуются бесконечным множеством значений по уровню (состояниям) и непрерывны во времени, хотя диапазон изменения значений непрерывного сигнала ограничен. Поэтому иногда такие устройства называют устройствами непрерывного действия
.
Дискретными устройствами
или устройствами дискретного действия
называют такие, у которых входные, выходные и промежуточные сигналы характеризуются счётным множеством значений по уровню и существованием в определённые интервалы времени. Такие сигналы можно отобразить в той или иной позиционной системе счисления (соответствующими цифрами). Например, в десятичной системе счисления либо двоичной системе счисления. Двоичное представление сигналов нашло наибольшее применение в технике и в формальной логике при исчислении высказываний и при выводе умозаключений из нескольких посылок. Поэтому дискретные устройства называют логическими
(по аналогии с формальной двоичной логикой) или цифровыми
, принимая во внимание возможность описания их с помощью чисел позиционной системы счисления.
Недостатки технических средств аналоговой техники
1. Наличие «дрейфа» и «шумов». Дрейф
- это медленное изменение сигнала, обусловленное дискретной природой явлений, по отношению к заданному его значению. Например, для электрических сигналов дискретную природу протекания электрического тока обуславливают электроны и «дырки», являющиеся носителями электрических зарядов. Шумы
- это случайные изменения сигнала, вызванные внешними или внутренними факторами, например, температурой, давлением, напряжённостью магнитного поля Земли и т.д.
2. Методологические трудности в определении понятий «равенство нулю» и «равенства аналоговых сигналов». И как следствие существование проблемы «обеспечения заданной точности (погрешности)» преобразований и передачи сигналов.
3. Возможность появления неустойчивых режимов работы и существование проблемы «обеспечения устойчивости» работы систем и устройств. Неустойчивый режим характеризуется возникновением в устройстве или системе незатухающих колебаний в изменении некоторых сигналов. В электронике это явление широко используется при построении генераторов импульсов и генераторов гармонических колебаний.
4. Технические трудности в реализации запоминающих устройств и устройств временной задержки аналоговых сигналов.
5. Недостаточный уровень интеграции аналоговых элементов и их универсальности.
6. Сравнительно малая дальность передачи аналоговых сигналов, обусловленная рассеянием энергии в линиях связи.
7. Сравнительно большое потребление энергии, так как аналоговые элементы работают на линейных участках их переходных характеристик и «потребляют» энергию в начальных (исходных) состояниях.
Достоинства технических средств аналоговой техники
1. Адекватность отображения физических процессов и закономерностей: и те и другие описываются непрерывными зависимостями. Это позволяет существенно упрощать принципиальные технические решения аналоговых устройств и систем.
2. Оперативность и простота изменения режимов работы: часто достаточно изменить сопротивление резистора или ёмкость конденсатора, чтобы неустойчивый режим сменился на устойчивый либо обеспечить заданный переходный процесс в устройстве.
3. Отсутствие необходимости в преобразовании аналоговых величин в дискретные. Эти преобразования сопровождаются погрешностью и определённой тратой времени.
Достоинства технических средств цифровой техники
1. Возможность программного управления, что увеличивает гибкость изменения структуры и алгоритма функционирования систем, позволяет упростить реализацию адаптивных законов управления.
2. Простота обеспечения заданной надёжности, точности и помехоустойчивости работы систем.
3. Простота обеспечения совместимости устройств с устройствами обработки информации в цифровой форме (ЭВМ, компьютерами).
4. Высокая степень конструктивной и функциональной интеграции, универсальности с возможностью построения систем по типовым проектным решениям. В свою очередь это позволяет сокращать затраты на производство и эксплуатацию систем и устройств.
5. Возможность проектирования формальными логическими методами, что позволяет сокращать сроки проектирования устройств и даёт возможность изменения функций устройств (и систем на их основе) методами агрегатного построения в процессе эксплуатации.
Недостатки технических средств цифровой техники
1. Необходимость преобразования аналоговых сигналов в дискретные. Эти преобразования сопровождаются появлением погрешности и задержками во времени.
2. Относительная сложность изменения режимов работы. Для этого необходимо менять структуру системы либо алгоритм её функционирования.
3. Сложность процессов анализа функционирования систем, как при проверке правильности их работы, так и при поиске возникающих неисправностей. Цифровые устройства характеризуются большой функциональной сложностью, что требует специальных «диагностических» устройств, которые изучаются в специальной области техники, называемой технической диагностикой
.
4. Повышенные требования к культуре производства и к культуре обслуживания технических средств цифровой техники. В свою очередь, это стимулирует необходимость повышения квалификации обслуживающего персонала и требует от него высокой квалификации.
Сравнительный анализ перечисленных достоинств и недостатков даёт вывод в пользу
технических средств цифровой техники
. Поэтому в настоящее время цифровые устройства широко внедряются, казалось бы, в традиционные области аналоговой техники: телевидение, телефонную связь, в технику звукозаписи, радиотехнику, в системы автоматического управления и регулирования.
1. Основы микроэлектронной техники
1.1. Основные понятия и определения
Микроэлектроника - основное направление электроники, которое изучает проблемы конструирования, исследования, создания и применения электронных устройств с высокой степенью функциональной
и конструктивной
интеграции
.
Микроэлектронное изделие
, реализованное средствами интегральной технологии и выполняющее определённую функцию по преобразованию и обработке сигналов, называется интегральной микросхемой
(ИМС) или просто интегральной схемой
(ИС).
Микроэлектронное устройство
- совокупность взаимосвязанных ИС, выполняющая законченную достаточно сложную функцию (либо несколько функций) по обработке и преобразованию сигналов. Микроэлектронное устройство может быть конструктивно оформлено в виде одной микросхемы либо на нескольких ИМС.
Под функциональной интеграцией
понимают увеличение числа реализуемых (выполняемых) некоторым устройством функций. При этом устройство рассматривается как единое целое
, неделимое. А конструктивная интеграция
- это увеличение количества компонентов в устройстве, рассматриваемом как единое целое
. Примером микроэлектронного устройства с высокой степенью конструктивной и функциональной интеграции, является микропроцессор
(см. выше), который, как правило, выполняется в виде одной «большой» ИМС.
Схемотехника
является частью микроэлектроники, предметом которой являются методы построения
устройств различного назначения на микросхемах широкого применения
. Предметом же цифровой схемотехники
являются методы построения (проектирования) устройств только на цифровых ИМС.
Особенностью цифровой схемотехники
является широкое применение для описания процессов функционирования устройств формальных
либо формально-естественных языков
и основанных на них формализованных методов проектирования
. Формальными языками являются булева алгебра
(алгебра логики, алгебра Буля) и язык «автоматных» логических функций -алгебра состояний и событий
. Благодаря использованию формализованных методов, достигается многовариантность
в решении прикладных задач, появляется возможность оптимального выбора схемотехнических решений
по тем или иным критериям.
Формальные методы
характеризуются высоким уровнем абстракции - отвлечения, пренебрежения частными свойствами описываемого объекта. Акцентируется внимание только на общих закономерностях во взаимных связях между компонентами объекта - его составными частями. К таким “закономерностям”, например, относятся правила арифметических действий в алгебре чисел (правила сложения, вычитания, умножения, деления). При этом отвлекаются от смысла чисел (количество ли это яблок, либо столов и т.д.). Эти правила строго формализованы, формализованы и правила получения сложных арифметических выражений, а также процедуры вычислений по таким выражениям. В таких случаях говорят, формальными являются и синтаксис
и грамматика языка
описания.
У формально-естественных языков синтаксис формализован, а грамматика (правила построения сложных выражений) подчиняется грамматике естественного языка, например русского либо английского. Примерами таких языков являются различные табличные языки описания. В частности, теоретической базой описания цифровых устройств является «Теория конечных автоматов» [1] или «Теория релейных устройств и конечных автоматов» [2].
1.2. Классификация микроэлектронных устройств
Всё многообразие микроэлектронных устройств (МЭУ) можно классифицировать по различным признакам:
· по принципу и характеру действия;
· по функциональному назначению и выполняемым функциям;
· по технологии изготовления;
· по области применения;
· по конструктивному исполнению и техническим характеристикам и так далее.
Рассмотрим теперь более детально разделение МЭУ по классификационным признакам.
По принципу
(характеру) действия
все МЭУ подразделяются на аналоговые
и цифровые
. Выше уже были даны понятия аналоговых и дискретных устройств и, в том числе цифровых. Здесь же отметим, если в дискретных устройствах все сигналы принимают только два условных значения - логического нуля (лог.0) и логической единицы (лог.1), то устройства называют логическими
. Как правило, все цифровые устройства относятся к логическим устройствам.
В зависимости от выполняемых функций (функционального назначения) различают следующие микроэлектронные устройства:
I. Аналоговые
1.1. Усилительные устройства (усилители).
1.2. Функциональные преобразователи, выполняющие математические операции с аналоговыми сигналами (например, интегрирование, дифференцирование и т.д.).
1.3. Измерительные преобразователи и датчики физических величин.
1.4. Модуляторы и демодуляторы, фильтры, смесители и генераторы гармонических колебаний.
1.5. Запоминающие устройства.
1.6. Стабилизаторы напряжений и токов.
1.7. Интегральные микросхемы специального назначения (например, для обработки радио- и видеосигналов, компараторы, коммутаторы и т.д.).
II. Цифровые МЭУ
2.1. Логические элементы.
2.2. Шифраторы, дешифраторы кодов и кодопреобразователи.
2.3. Запоминающие элементы (триггеры).
2.4. Запоминающие устройства (ОЗУ, ПЗУ, ППЗУ, ПЛМ и др.).
2.5. Арифметико-логические устройства.
2.6. Селекторы, формирователи и генераторы импульсов.
2.7. Счётные устройства (счётчики импульсов).
2.8. Цифровые компараторы, коммутаторы дискретных сигналов.
2.9. Регистры.
2.10. Микросхемы специального назначения (например, таймерные, микропроцессорные комплекты ИС и т.д.).
Приведённая классификация далеко не исчерпывающая, но позволяет сделать вывод, что номенклатура цифровых устройств значительно шире номенклатуры аналоговых МЭУ.
Кроме перечисленных, существуют микросхемы преобразователей уровней сигналов, например триггеры Шмита, у которых входные сигналы являются аналоговыми, а выходные - дискретными, двоичными. Такие микросхемы занимают промежуточное положение. Аналогично, микросхемы аналого-цифровых и цифро-аналоговых преобразователей (АЦП и ЦАП), коммутаторы аналоговых сигналов, управляющиеся дискретными сигналами, следует отнести к «промежуточным» МЭУ.
В зависимости от количества реализуемых функций различают однофункциональные
(простые) и многофункциональные
(сложные) МЭУ. В многофункциональных устройствах функции могут выполняться одновременно
либо последовательно
во времени. В зависимости от этого, в первом случае, устройства называют устройствами «параллельного» действия, а во втором случае - устройствами последовательного действия или «последовательностными». Если настройка многофункционального устройства на выполнение той или иной функции осуществляется путём коммутации входов (физической перекоммутацией электрических цепей), то такое устройство называют устройством с «жёсткой логикой
» работы. А если изменение выполняемых функций производится с помощью дополнительных внешних сигналов (на так называемых управляющих входах), то такие МЭУ следует отнести к «программно-управляемым». Например, ИМС арифметико-логических устройств (АЛУ) могут реализовать арифметические либо логические операции с двумя многоразрядными двоичными числами. А настройка на выполнение арифметических (либо логических) операций осуществляется одним дополнительным внешним сигналом, в зависимости от значения которого будут выполняться желаемые действия. Поэтому АЛУ следует отнести к программно-управляемым МЭУ.
По технологии изготовления
все ИМС делятся на:
1. Полупроводниковые;
2. Плёночные;
3. Гибридные.
В полупроводниковых
ИС все компоненты и соединения выполнены в объёме и на поверхности кристалла полупроводника. Эти ИС делятся на биполярные
микросхемы (с фиксированной полярностью питающих напряжений) и на униполярные
- с возможностью смены полярности питающего напряжения. В зависимости от схемотехнического исполнения «внутреннего содержания» биполярные микросхемы делятся на следующие виды:
· ТТЛ - транзисторно-транзисторной логики;
· ТТЛш - транзисторно-транзисторной логики с транзисторами и диодами Шотки;
· ЭСЛ - эмиттерно-связанной логики;
· И2
Л - инжекционной логики и другие.
Микросхемы униполярной технологии выполняются на МДП-транзисторах («металл–диэлектрик–полупроводник»), либо на МОП-транзисторах («металл–окисел–полупроводник»), либо на КМОП-транзисторах (комплиментарные «металл – окисел – полупроводник»).
В плёночных
ИС все компоненты и связи выполняются только на поверхности кристалла полупроводника. Различают тонкоплёночные
(с толщиной слоя менее 1 микрона) и толстоплёночные
с толщиной плёнки более микрона. Тонкоплёночные ИС изготавливаются методом термовакуумного осаждения и катодного распыления, а толстоплёночные - методом шелкографии с последующим вжиганием присадок.
Гибридные
ИС состоят из «простых» и «сложных» компонентов, расположенных на одной подложке. В качестве сложных компонентов обычно используются кристаллы полупроводниковых либо плёночных ИС. К простым относятся дискретные компоненты электронной техники (транзисторы, диоды, конденсаторы, индуктивности и т.д.). Все эти компоненты конструктивно располагаются на одной подложке и на ней также выполняются электрические соединения между ними. Причём одна подложка с расположенными на ней компонентами образуют один «слой» гибридной ИС. Различают однослойные
и многослойные
гибридные ИС. Многослойная гибридная ИС способна выполнять достаточно сложные функции по обработке сигналов. Такая микросхема равносильна по действию «микроблоку» устройств, либо, если она предназначена для самостоятельного применения, действию «целого» блока.
Кроме того, любые микросхемы оцениваются количественным показателем
их сложности
. В качестве такого показателя используется «степень
интеграции
» -k
,
равная десятичному логарифму от общего количества N
компонентов, размещённых на одном кристалле полупроводника, то есть
k
= lq
N
. (1)
В соответствии с формулой (1) все микросхемы делятся на микросхемы 1-й, 2-й, третьей и так далее степеней интеграции. Степень интеграции лишь косвенно характеризует сложность микросхем, поскольку принимается во внимание только конструктивная
интеграция. Фактически же сложность микросхемы зависит и от количества взаимных связей между компонентами.
В инженерной практике используется качественная характеристика сложности микросхем в понятиях «малая», «средняя», «большая» и «сверхбольшая» ИС.
В табл.1.1 приведены сведения о взаимном соответствии качественных и количественных мер сложности ИС по их видам.
Таблица 1.1
| Наименование ИС |
Вид ИС |
Технология изготовления |
Количество компонентов на кристалле |
Степень интеграции k
|
Малая (МИС)
|
Цифровая |
Биполярная |
1…100 |
1-я и 2-я
|
| Униполярная |
| Аналоговая |
Биполярная |
1…30 |
Средняя (СИС)
|
Цифровая |
Биполярная |
101…500 |
3-я
|
| Униполярная |
101…1000 |
| Аналоговая |
Биполярная |
31…100
|
| Униполярная |
Большая (БИС)
|
Цифровая |
Биполярная |
501…2000 |
4-я
|
| Униполярная |
1001…10000 |
| Аналоговая |
Биполярная |
101…300
|
| Униполярная |
Сверхбольшая (СБИС)
|
Цифровая |
Биполярная |
Более 2000 |
5-я
|
| Униполярная |
Более 10000 |
Аналоговая
|
Биполярная |
Более 300
|
| Униполярная |
Из анализа табл.1.1 следует, что в сравнении с цифровыми ИС аналоговые микросхемы при одинаковых степенях интеграции имеют в своём составе (на кристалле полупроводника) более чем в три раза, меньшее число компонентов. Это объясняется тем, что активные компоненты (транзисторы) аналоговой микросхемы работают в линейном режиме и рассеивают большее количество энергии. Необходимость отвода тепла, выделяющегося при рассеянии энергии, ограничивает количество компонентов, размещаемых на одном кристалле. У цифровых микросхем активные компоненты работают в ключевом режиме (транзисторы либо заперты, либо открыты и находятся в режиме насыщения). В этом случае рассеиваемая мощность незначительна, и количество выделяемого тепла также незначительно и следовательно число компонентов на кристалле может быть размещено больше. (Размеры кристаллов стандартизованы и ограничены.) При униполярной технологии объём кристалла, занимаемый под полевой транзистор приблизительно в три раза меньше объёма, занимаемого биполярным транзистором (n
-
p
-
n
или p
-
n
-
p
типа). Этим объясняется тот факт, что активных компонентов на кристалле стандартных размеров в униполярной микросхеме можно разместить больше.
По конструктивному исполнению
в зависимости от функциональной сложности микроэлектронные устройства подразделяются:
- на простые микросхемы (ИМС);
- на микросборки;
- на микроблоки.
ИМС
- микроэлектронное изделие, изготавливаемое в едином технологическом цикле
, пригодное для самостоятельного применения или в составе более сложных изделий (в том числе, микросборок и микроблоков). Микросхемы могут быть бескорпусными и иметь индивидуальный корпус, защищающий кристалл от внешних воздействий.
Микросборка
- микроэлектронное изделие, выполняющее достаточно сложную функцию (функции) и состоящее из электрорадиокомпонентов и микросхем, изготавливаемое с целью миниатюризации радиоэлектронной аппаратуры. По существу гибридные микросхемы являются микросборками. Самой простой микросборкой может быть, например, набор микрорезисторов, выполненных на кристалле полупроводника и оформленных в едином корпусе (как микросхема).
Микроблок
также является микроэлектронным изделием, состоит из электрорадиокомпонентов и интегральных схем и выполняет сложную функцию (функции).
Как правило, микросборки и микроблоки изготавливаются в различных технологических циклах, и, может быть, на разных заводах-изготовителях.
В качестве классификационных технических характеристик
обычно используются потребляемая мощность
(одной микросхемой) и быстродействие
.
По потребляемой мощности
все ИМС можно разделить на: а
) микромощные
(менее 10 мВт
); б
) маломощные
(не более 100 мВт
); в
) средней мощности
(до 500 мВт
) и г
) мощные
(более или = 0,5 Вт
).
По быстродействию
(максимальным задержкам времени распространения сигналов через ИС) микросхемы делятся условно на: а
) сверхбыстродействующие с граничной частотой f
гр
переключений свыше 100 МГц
; б
) быстродействующие (f
гр
от 50 МГц
до 100 МГц
); в
) нормального быстродействия (f
гр
от 10 МГц
до 50 МГц
). При этом задержки распространения составляют порядка от единиц наносекунд (10-9
с
.) до 0,1 микросекунды (1ms =10-6
с
.).
Цифровые микроэлектронные устройства, в том числе микросхемы и другие устройства дискретного действия
, удобно классифицировать по
характеру зависимости
выходных сигналов от входных. Как это принято в теории конечных автоматов. В соответствии с этим признаком все устройства принято разделять на комбинационные
и последовательностные
.
В комбинационных устройствах
значения выходных сигналов в какой-либо момент времени однозначно определяются значениями входных сигналов в этот же момент времени. Поэтому можно считать, что работа таких устройств не зависит от времени. Их ещё называют устройствами «без памяти
», однотактными
устройствами или устройствами однотактного действия. В теории конечных автоматов комбинационные устройства называют «примитивными конечными автоматами».
В последовательностных устройствах
значения выходных сигналов (выходные сигналы) зависят от значений входных сигналов не только в рассматриваемый момент времени, но и от значений входных сигналов в предыдущие моменты времени. Поэтому такие устройства называют устройствами с «памятью
», многотактными
устройствами, а в теории конечных автоматов, просто − конечным автоматом
(не тривиальным).
При рассмотрении учебного материала, в дальнейшем, за основную
примем именно эту классификацию
, так как методы построения
(синтеза) и процессы функционирования названных устройств существенно различаются
.
Заканчивая изложение вопросов классификации, отметим, что приведённый перечень классификационных признаков и перечень наименований микроэлектронных изделий (микросхем) далеко не исчерпывающий. В дальнейшем, по мере необходимости, этот перечень мы дополним.
1.3. Логические элементы
Логические элементы относятся к простейшим комбинационным «устройствам», имеющим один выход и один-два входа. Своё название они получили по той причине, что их функционирование полностью можно описать логическими функциями
и в частности булевыми функциями.
Как и в формальной логике, все высказывания могут быть истинными либо ложными, так и логические функции могут принимать только два условных значения: логической единицы (лог.1) - «истина» и логического нуля (лог.0) - «ложь».
При описании работы логических элементов выходным сигналам
ставят в однозначное соответствие функции, а входным сигналам
-аргументы этих функций. Таким образом, и функции, и аргументы функций, а также входные и выходные сигналы логических элементов являются двоичными. Если пренебречь реальным временем перехода логического элемента из одного состояния (состояния лог.1) в другое (состояние лог.0), то ни аргументы и ни функции не будут зависеть от фактора времени - переменной времени. Правила получения и преобразования логических выражений рассматривает алгебра логики или булева
алгебра.
Основными логическими функциями
в алгебре логики принято считать функции от двух
аргументов. Им даны названия, введены логические символы для обозначения соответствующих логических операций при их записи в алгебраической форме, а также эти символы используются в условных графических обозначениях (УГО) логических элементов в схемной документации.
Прежде чем рассматривать непосредственно виды логических элементов, рассмотрим вначале общий вопрос о системе обозначений микросхем, содержащих логические элементы. Такие микросхемы относятся к микросхемам малой степени интеграции
.
1.3.1. Система условных цифробуквенных обозначений ИМС логических элементов
В отечественной технической литературе, а также при маркировке ИМС отечественного производства, при их изготовлении на заводах-изготовителях, принята 4-х элементная форма обозначений микросхем (рис.1.1).
Первым
элементом
в обозначении является цифра
, которой указывается группа конструктивно-технологического исполнения ИС. Эта цифра может принимать следующие значения:
1, 5, 6, 7 - соответствуют полупроводниковым ИС. Причём цифра 7 используется для обозначения только бескорпусных ИМС;
2, 4, 8 - это гибридные микросхемы;
3 - прочие микросхемы, в том числе, и плёночные.
Перед первым элементом обозначения может стоять буква или две буквы (русского алфавита), они не обязательны, но ими обозначают тип и материал корпуса микросхемы и возможности её применения. Например, буквой К обозначают микросхемы широкого применения
в пластмассовом
корпусе первого типа. Есть микросхемы специального применения, например, для устройств, эксплуатируемых в условиях тропического климата.
Второй
элемент
- 2 или 3 цифры, ими обозначают порядковый номер
серии
микросхем. Всё множество выпускаемых отечественной промышленностью микросхем делится на серии.
Серия ИМС - это совокупность ИС единого конструктивно-технологического исполнения, выполняющих различные функции и предназначенных для совместного применения.
Третьим
элементом
в обозначении являются две русские
буквы
, первая из которых обозначает подгруппу ИС по функциональному назначению, а вторая буква соответствует виду ИС также по функциональному назначению микросхемы. Например, первая буква Л «говорит», что это ИС логических элементов (подгруппа логика
), вторая буква А соответствует логическим элементам вида И-НЕ. В табл.1.2 приведены наиболее употребительные буквенные коды видов ИС по выполняемым функциям.
 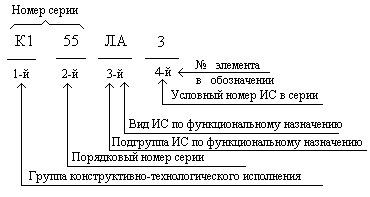 И, наконец, 4-мэлементом
в обозначениях микросхем являются одна
или две
цифры
, обозначающие условный номер микросхемы в рассматриваемой серии. Так, приведённый на рис.1.1 пример обозначения соответствует обозначению полупроводниковой микросхемы серии К155, широкого применения, в пластмассовом корпусе 1-го типа. В её состав входят 4 двухвходовых логических элементов вида И-НЕ (2И-НЕ). И, наконец, 4-мэлементом
в обозначениях микросхем являются одна
или две
цифры
, обозначающие условный номер микросхемы в рассматриваемой серии. Так, приведённый на рис.1.1 пример обозначения соответствует обозначению полупроводниковой микросхемы серии К155, широкого применения, в пластмассовом корпусе 1-го типа. В её состав входят 4 двухвходовых логических элементов вида И-НЕ (2И-НЕ).
Обычно четвёртым элементом в обозначении ИМС «зашифровывается» порядковый номер модификации элементов одного вида, различающихся числом входов и способом «организации» выхода.
Кроме названных обозначений, согласно ГОСТ 2.743-91 «Условные графические обозначения в электрических схемах. Элементы цифровой техники», используются другие двухбуквенные коды для обозначения функционального назначения микросхем, например: ИД - декодеры- демультиплексоры, дешифраторы, ИР - регистры, КП - коммутаторы дискретных сигналов и так далее. В частности, буква И соответствует подгруппе микросхем, используемых для построения вычислительных цифровых устройств.
Различные серии ИС отличаются количеством микросхем и их номенклатурой (типономиналами). Типономинал ИС - конкретное условное обозначение, содержащее основные сведения о микросхеме. В процессе развития технологии количество типономиналов ИМС конкретной серии может увеличиваться.
Среди серий микросхем наиболее функционально развиты ИМС транзисторно-транзисторной логики (ТТЛ и ТТЛш). Эти серии характеризуются широкой номенклатурой ИС, поэтому изложение учебного материала будем в основном иллюстрировать примерами этих микросхем.
В указанном выше ГОСТе содержатся также условные графические обозначения логических элементов и приведены правила формирования УГО более сложных логических элементов и модулей. Поэтому следует, прежде всего, ознакомиться с указанным ГОСТом.
Таблица 1.2

| Вид ИС |
Обозначение |
| Элементы И-НЕ |
ЛА |
| Элементы И-НЕ /ИЛИ-НЕ |
ЛБ |
| Расширители по ИЛИ |
ЛД |
| Элементы ИЛИ-НЕ |
ЛЕ |
| Элементы И |
ЛИ |
| Элем. И-ИЛИ-НЕ/И-ИЛИ |
ЛК |
| Элементы ИЛИ |
ЛЛ |
| Элементы ИЛИ-НЕ/ИЛИ |
ЛМ |
| Элементы НЕ |
ЛН |
| Прочие элементы |
ЛП |
| Элементы И-ИЛИ-НЕ |
ЛР |
| Элементы И-ИЛИ |
ЛС |
1.3.2. Применение булевой алгебры для описания
логических элементов и устройств
Как уже было отмечено выше, функционирование логических элементов можно описать логическими (булевыми) функциями. В свою очередь логические функции можно определить (задать), перечислив все условия, при которых функция принимает значение лог.1, т.е. по условиям истинности, так и по условиям ложности (значения лог.0). Аналогично, рассматривая работу логического (какого-либо) элемента, можно перечислить все условия, при которых на выходе появляется сигнал лог.1, либо условия, когда на выходе элемента будет присутствовать сигнал лог.0. В этом заключается принцип дуальности (двойственности) в описании логических устройств.
В технике, при описании работы различных устройств, широко используется понятие «активного», в противоположность ему, «неактивного» значения какого-либо сигнала. При этом под активным
значением (уровнем) сигнала понимается такое действие, которое вызывает на выходе устройства желаемое действие или, по-другому, устройство оказывает активные действия на внешние устройства. Наоборот, неактивные действия оказывают пассивное действие на внешние устройства. Так, в логике обычно акцентируют внимание на истинности высказываний, поэтому истинность высказываний следует считать по умолчанию их активным значением. Аналогично, при описании технических устройств можно акцентировать внимание на условиях их «срабатывания» либо на условиях «несрабатывания».
Соглашения, при которых сигнал лог.1 считается активным, называют соглашениями «положительной» логики
. Наоборот, когда за активное значение принимается уровень лог.0, такие соглашения называют соглашениями «отрицательной» логики
. Как правило, за сигнал лог.1 принимается более «высокий» уровень, а за сигнал лог.0 «низкий» уровень сигналов. Например, при использовании ИМС ТТЛ сигналом лог.1 считается напряжение не менее +2,4 В,
а сигналом лог.0 - напряжение больше нуля, но не больше 0,4 В
. Это - стандартные уровни сигналов в устройствах на ИМС ТТЛ.
Описания, составленные при соглашениях положительной логики
и при соглашениях отрицательной логики
, логически эквивалентны, так как описывают одно и тоже устройство. Однако сложность
технической реализации
логических устройств в зависимости от выбранного соглашения может оказаться существенно различной
. Поэтому всегда возникает проблема выбора способа описания с целью получения наиболее простого технического решения.
Как уже было сказано, основными функциями алгебры логики являются функции двух переменных
. Можно составить эти функции чисто формально, придавая аргументам всевозможные значения (комбинации их значений), и затем придать функциям так же всевозможные значения. Поскольку и аргументы и функции могут принимать только два значения, то нетрудно определить число комбинаций, составленных из аргументов, и число всех возможных функций. Пусть число аргументов будет n
, а количество их комбинаций N
, тогда
N
= 2n
. (1.1)
Число же всевозможных логических функций тогда можно рассчитать по формуле
M
= 2N
=  . (1.2) . (1.2)
Как видно из формулы (1.2), число булевых (логических) функций быстро растёт с увеличением числа аргументов n
. Так, при n
=2 получим N
=22
=4, а М
=24
=16, т.е. шестнадцать логических функций от двух аргументов.
В табл. 1.3 приведены названия и обозначения функций, их значения на том или ином наборе значений аргументов a
и b
, а также алгебраические выражения этих функций в дизъюнктивной совершенной нормальной форме
(ДСНФ) и конъюнктивной совершенной нормальной форме
(КСНФ).
Из анализа этой таблицы следует, что среди множества приведённых функций есть функции-константы «нулевая» и «единичная», функции «повторения» и «инверсии» (функции НЕ) входных переменных a
и b
, фактически являющиеся функциями одного аргумента, и есть функции, которые существенно зависят от двух аргументов.
В приведённых алгебраических выражениях знаком + (плюс) обозначена операция логического сложения (дизъюнкции), чертой над переменной или над логическим выражением обозначена операция инверсии, а символы логического умножения (произведения) пропущены.
Таблица 1.3
Логические функции двух аргументов
| № п/п |
Название функции
|
Значения функции при значениях аргументов |
Обозначение |
Алгебраические формы функций |
| а b
|
0 |
0 |
1 |
1 |
ДСНФ
|
КСНФ
|
| 0 |
1 |
1 |
0 |
V0
|
Нулевая |
0
|
0
|
0
|
0
|
0
|
-
|
 |
| V1
|
Запрет b
|
0
|
0
|
0
|
1
|
a
¬b
|

|
 |
V2
|
Конъюнкция (И) |
0
|
0
|
1
|
0
|
a
&b
или
ab
|
ab
|
 |
V3
|
Повторение а
|
0 |
0 |
1 |
1 |
а
|
  |
 |
V4
|
Запрет а
|
0
|
1
|
0
|
0
|
b
¬a
|

|
 |
V5
|
Неравнозначность |
0
|
1
|
0
|
1
|
a
Åb
|

|

|
| V6
|
Повторение b
|
0 |
1 |
1 |
0 |
b |
 |
 |
V7
|
Дизъюнкция (функция ИЛИ) |
0
|
1
|
1
|
1
|
a
+b
|

|
a
+b
|
V8
|
Пирса (ИЛИ-НЕ) |
1
|
0
|
0
|
0
|

|

|
 |
| V9
|
Инверсия b
(НЕ ) |
1 |
0 |
0 |
1 |
 |
 |
V10
|
Равнозначность |
1 |
0
|
1
|
0
|

|

|

|
| V11
|
Импликация b
|
1 |
0 |
1 |
1 |
b
®a
|
 |
 |
| V12
|
Инверсия а
|
1 |
1 |
0 |
0 |
 |
 |
| V13
|
Шеффера (И-НЕ) |
1 |
1 |
0 |
1 |
 |
 |
 |
| V14
|
Импликация а
|
1 |
1 |
1 |
0 |
a
®b
|
 |
 |
V15
|
Единичная |
1
|
1
|
1
|
1
|
1
|
 |
-
|
Функции-константы фактически выражают независимость от аргументов и, в то же самое время, их можно считать «функциями» от большого числа аргументов. Обратите внимание, нулевая
функция не имеет ДСНФ, поскольку она никогда не принимает значение лог.1, а единичная
функция не имеет КСНФ, так как она никогда не принимает значение лог.0. Отсюда следует вывод, что ДСНФ соответствует описанию
(заданию) логических функций по условиям истинности
(по лог.1), а КСНФ -по условиям ложности
(по лог.0). Любая логическая функция, кроме функций-констант, имеет как ДСНФ, так и КСНФ. Это соответствует тому, что любое логическое устройство (сколь сложно оно ни было бы) можно описать по условиям срабатывания и по условиям несрабатывания.
Значения функций «повторения» и «инверсии» (V3
, V6
, V9
, V12
) либо повторяют значения одного из аргументов, либо принимают противоположные (инверсные) ему значения. Поэтому они и получили такие названия.
Функции инверсии
чаще всего называют функциями НЕ. Эти функции реализуются логическими элементами НЕ (или инверторами). Функции повторения реализуются повторителями. Принято говорить, что функции инверсии и повторения «несущественно
» зависят от второго аргумента, хотя их можно представить как функции двух, трёх и большего числа аргументов.
В технике функции «Неравнозначности» и «Равнозначности» более известны под названиями «сумма по модулю два (по mod 2)» и «инверсия суммы по mod 2» соответственно. Функции Шеффера и Пирса, соответственно, известны под названиями «инверсия логического произведения» (функции И-НЕ) и «инверсии логической суммы» (ИЛИ-НЕ). Эти функции реализуются одноимёнными по названию логическими элементами.
В булевой алгебре и в дальнейшем в логических выражениях принято обозначать функции
прописными буквами
латинского алфавита, а аргументы
функций -строчными
(малыми) буквами
того же алфавита.
1.3.3. Способы и формы задания логических функций
При описании логических устройств оказывается, что способ задания (определения) логических функций и форма их представления существенно влияют на трудность достижения конечного результата. В зависимости от поставленной цели способы задания и формы представления функций могут быть различными. Например, при построении логических устройств на программируемых постоянных запоминающих устройствах (ППЗУ) алгебраические формы логических функций нежелательны и не целесообразны. Однако при построении устройств на микросхемах малой степени интеграции, на ИМС логических элементов, требуются минимальные алгебраические формы логических функций, так как в противном случае не обеспечить минимальные аппаратурные затраты. Таким образом, выбор способа задания зависит от поставленной цели описания устройств.
Различают табличный
, матричный
, графический
и аналитический
способы задания.
При табличном
задании используются так называемые «таблицы истинности
» логических функций, в которых указываются значения функций на всём множестве комбинаций их аргументов. Таким образом число столбцов в таблице истинности определяется числом аргументов и числом функций, а количество строк - по формуле (1.1). Таблицы истинности используются для общего ознакомления с работой комбинационных устройств, когда число входов (аргументов функций) и число выходов (число функций) не превышает 4-х. Таблицы истинности становятся громоздкими при большем числе аргументов, а поэтому они мало пригодны для анализа. По таблицам истинности достаточно просто отыскиваются алгебраические формы функций в ДСНФ либо в КСНФ, а для поиска минимальных алгебраических форм они непригодны.
Матричный
способ задания (или задание функций с помощью булевых матриц
) основан на графическом отображении всего множества комбинаций аргументов функции на «плоскости» (в двумерном пространстве). Понятие «булевы матрицы» было введено А.Д. Закревским, им же был предложен визуально-матричный
метод минимизации логических функций [3]. В зарубежной литературе этот способ задания и минимизации логических функций известен под названием «метода задания и минимизации с помощью карт Карно
». (Не следует путать понятие «матриц», используемое в математике, с понятием «булевы матрицы»). Наряду с понятием булева
матрица
в дальнейшем будет употребляться понятие карта Карно
, как понятия синонимы.
Булева матрица представляет собой прямоугольник с соотношением сторон 1:2 (при нечётном числе аргументов функции) или квадрат (при чётном числе аргументов), разделённые на элементарные квадраты (клетки). Число клеток в матрице всегда кратно степени двойки и определяется формулой (1.1). Таким образом, количество элементарных квадратов равно полному множеству комбинаций, составленных из аргументов функции. Сверху справа
и слева сбоку
матрицы прямоугольными скобками либо сплошной прямой линией размечаются области единичных значений аргументов (рис.1.2). Причём эти скобки помечают идентификаторами аргументов, которые размещают под скобкой либо справа (внизу) скобок. Условно считают, что область, ограниченная скобкой, является областью единичных значений аргумента, а вне этой области аргумент имеет нулевое значение. Таким образом, помеченная карта Карно, как бы «кодируется» комбинациями аргументов. При этом каждой клетке будет соответствовать одна вполне конкретная комбинация аргументов функции. Сама карта помечается идентификатором функции
внизу
либо справа
.
Чтобы задать картой какую-либо функцию, необходимо поставить в соответствующие клетки значения этой функции (0 или 1, либо ~).
Так, на рис.1.2 приведены карты Карно для функций 4-х, 5-ти и 6-ти аргументов.
В частности, функции X и Y полностью определены, а функция Z недоопределена, так как наряду с фиксированными значениями 1 и 0 в клетках показаны «условные» значения, помеченные символом ~ (типографский символ - тильда). Условные
значения логических функций используют в тех случаях, когда конкретные значения (0 либо 1) нельзя определить заранее. Такие случаи возникают, например, при синтезе устройств по неполностью заданным условиям, либо когда комбинации аргументов, соответствующих клеткам с символом ~ не могут возникнуть по каким-либо причинам. В процессе отыскания минимальных логических выражений недоопределённых функций, эти условные значения доопределяют значениями 1 либо 0, стараясь получить наиболее простые алгебраические выражения.
В принципе матричная форма задания логических функций более удобна для поиска минимальных алгебраических форм функций вплоть до 10 (и более) аргументов. Последовательность построения карты Карно для функций от большого числа аргументов можно уяснить, сопоставляя рис.1.2,а
с рисунками 1.2,б
и в
.
Графический
способ задания логических функций основан на использовании n
-мерных кубов. Размерность куба определяется числом n
аргументов функции, например, функцию от трёх аргументов можно задать 3-мерным кубом, каждая вершина которого соответствует определённой комбинации аргументов. Чтобы задать функцию с помощью 3-мерного куба, вершины куба соответствующим образом помечают. Этот способ не нашел широкого применения, и мы им пользоваться не будем.
Аналитический
способ задания функций используется наиболее широко для отыскания функциональных схем
синтезируемых устройств. Благодаря условным графическим обозначениям (УГО) логических элементов, существует возможность непосредственно от алгебраического выражения адекватно перейти к функциональной схеме и, наоборот, по функциональной схеме получить алгебраическое выражение функции, описывающей выходной сигнал устройства. Кроме того, пользуясь законами и следствиями алгебры логики можно выполнять эквивалентные преобразования логических выражений и, тем самым, получать новые варианты функциональных схем.
В булевой алгебре различают несколько видов алгебраических форм функций, в частности, в табл.1.3 были приведены две формы ДСНФ и КСНФ. Первая получается, когда функция определяется условиями истинности (по 1), а вторая - когда функция определяется по «нулям».
Например, функция Х, заданная картой рис.1.2,а
, будет иметь следующие совершенные формы:
ДСНФ:
 (1.3) (1.3)
КСНФ:
 (1.4) (1.4)
Как видно по рис.1.2,а
, так и из выражений (1.3) и (1.4), следует, что функция принимает значение «1», если нечётное число аргументов принимают значение лог.1, в противном же случае она принимает значение «0». Такие функции реализуются схемами «контроля чётности/нечётности» или логическими элементами «сумма по mod2». Если использовать условное обозначение суммы по mod2 (функция неравнозначности V5
в табл.1.3), то можно записать
X
= a
Åb
Åc
Åd
. (1.5)
Это выражение более короткое и оно эквивалентно выражению (1.3). Обратите внимание (рис.1.2,а
), функции сумма по mod2 и её инверсии соответствует «шахматный узор» на карте Карно. Этим можно будет пользоваться в дальнейшем при поиске иных алгебраических форм логических функций. Кстати, эти функции не имеют нормальных минимальных
дизъюнктивных и конъюнктивных форм - МДНФ и МКНФ.
Рассмотрим часто применяемые ИМС логических элементов, при этом будем использовать различные формы описания логических функций, реализуемых этими элементами.
1.3.4. Логические элементы НЕ
Это - наиболее простые элементы, имеющие один вход и один выход. Такие элементы описываются логической функцией отрицания, инверсии и называются просто функциями НЕ. На рис.1.3 приведены УГО элементов НЕ, рекомендуемые ГОСТом. Как видно, указатель инверсии допускается ставить либо по выходу, либо по входу логического элемента. Согласно ГОСТ можно не ставить метку основной функции «1» в основном поле УГО.
Алгебраическое выражение функции инверсии имеет вид
 Х
= Х
= 
 и читается «не а
». Выходной сигнал элемента НЕ принимает всегда противоположное значение по отношению к значениям входного сигнала. Есть несколько разновидностей ИМС логических элементов, отличающихся способом организации выхода. Например, в ИМС серии К155 есть микросхемы К155ЛН1, содержащих в своём составе 4 логических элемента НЕ со стандартной нагрузочной способностью. Есть элементы НЕ с повышенной нагрузочной способностью, однако все они описываются одним и тем же логическим выражением. и читается «не а
». Выходной сигнал элемента НЕ принимает всегда противоположное значение по отношению к значениям входного сигнала. Есть несколько разновидностей ИМС логических элементов, отличающихся способом организации выхода. Например, в ИМС серии К155 есть микросхемы К155ЛН1, содержащих в своём составе 4 логических элемента НЕ со стандартной нагрузочной способностью. Есть элементы НЕ с повышенной нагрузочной способностью, однако все они описываются одним и тем же логическим выражением.
Логические элементы «повторители» так же имеют один вход и один выход, но выходной сигнал повторяет значение входного сигнала. Такие элементы используются для «развязки» выходов логических элементов и для повышения их нагрузочной способности.
1.3.5. Логические элементы И
Эти элементы реализуют функцию логического умножения (конъюнкции). Функции являются как минимум двухместными либо многоместными и описываются следующими логическими выражениями:
X
= a
&b
= a
Ù b
= a
·b
= ab
. (1.6)
Символы конъюнкции & и Ù допускается заменять точкой, либо совсем не ставить. Выходной сигнал элемента И
принимает значение лог.1 только в том случае, если все входные сигналы принимают значение лог.1. На рис.1.4 приведены условные графические обозначения и карты Карно для двухвходового (рис.1.4,а
и б
) и трёхвходового (рис.1.4,в
и г
) логического элемента И
.
Рис.1.4. Условные графические обозначения элементов И: двухвходового (а
),
трёхвходового (в
), карты Карно логических функций 2И (б
) и 3И (г
)
Как видно из приведённых булевых матриц, конъюнкция равна лог.1 только в единственном случае, когда все аргументы -и первый
, и
второй
, и
третий
и
т.д. - одновременно принимают значение лог.1. Поэтому такие элементы называют схемами совпадения
, реже встречается название «конъюнкторы», а описывающие их функции, иногда - функциями И. В сериях ИМС выпускаются различные логические элементы И
, например, микросхема К155ЛИ1 содержит 4 элемента 2И (двухвходовых). Отличие заключается в разном числе входов у различных элементов.
Приведёнными на рис.1.4,б
и рис.1.4,г
матрицами иллюстрируются правила логического умножения
, а показанные УГО соответствуют соглашениям положительной логики
.
Благодаря справедливым в булевой алгебре переместительному и сочетательному законам, входы
логических многовходовых элементов И
являются логически равнозначными
, а многовходовой логический элемент И
можно получить из нескольких двухвходовых элементов И
. Так, на рис.1.5 приведе
ны два варианта построения логического элемента И
с шестью входами (6И) на двухвходовых элементах И
(2И).
Все приведённые на рис.1.5 схемы логически эквивалентны и, в свою очередь, они эквивалентны условному графическому обозначению 6-тивходового логического элемента И
(рис.1.5,в
). Вместе с тем, схемы описываются различными по форме записи логическими выражениями:
X
= ((((a
·b
)·c
)·d
)·k
)·m
― схема рис. 1.5,а
; (1.7)
Y
= ((ab
)·(cd))·(km
) ― схема рис. 1.5,б
; (1.8)
а условному обозначению элемента 6И соответствует следующее выражение:
Z
=abcdkm
. (1.9)
Хотя в соответствии с упомянутыми законами булевой алгебры от перемены мест сомножителей логическое произведение не меняется и скобки в выражениях логического произведения можно не ставить, тем не менее, выражения (1.7), (1.8) и (1.9) несут информацию о способах построения
схем
. Таким образом, указанные выражения можно считать «логико-математическими моделями» приведённых схем и в том числе УГО элемента 6И.
Следует заметить, что при описании логических комбинационных устройств с помощью булевых выражений, как правило, абстрагируются от фактора времени. Такое описание соответствует описанию устройств в статике - при установившихся значениях входных сигналов (и переменных). Считается, что изменение входных и выходных сигналов происходят мгновенно, аналогично меняются значения аргументов и значения самих логических функций. В то же самое время реальные элементы имеют конечное время перехода из одного состояния в другое или, как принято говорить, обладают конечным (не равным нулю) временем распространения сигналов от входов к выходу элемента либо устройства. С учётом сказанного, следует отдать предпочтение схеме рис.1.5,б
, в которой время распространения сигналов от входов, помеченных аргументами функций, к выходу схемы в среднем меньше. В источнике [5] содержатся сведения о временных логических функциях, которые можно применять для описания схем с временными задержками.
1.3.6. Логические элементы ИЛИ
Логическими элементами ИЛИ реализуется логическая сумма
нескольких двоичных сигналов (и входных переменных). Функция, описывающая такие элементы, называется дизъюнкцией
или функцией логического сложения
. На рис.1.6 приведены условные обозначения (УГО) элементов ИЛИ и карты Карно описывающих их функций.
Алгебраическое выражение логической суммы двух переменных a
и b
записывается следующим образом
X
= a
Úb
= a
+ b
. (1.10)
В булевой алгебре для обозначения дизъюнкции используется символ Ú. В технических же её приложениях обычно применяется знак + (арифметического сложения), но только тогда, когда это не приводит к некорректности при записи формул и логических выражений. (Преимущественно этот знак будет использоваться в дальнейшем для обозначения дизъюнкции.)
Как видно из карт рис.1.6,б
и рис.1.6,г
, функция логического сложения принимает значение лог.0 только в единственном случае, когда все аргументы принимают значение лог.0. Значение же лог.1 она имеет, если первый аргумент или
второй, или
третий и т.д., или
все вместе аргументы принимают значение лог.1. Поэтому эту функцию называют функцией ИЛИ.
Так же, как и к конъюнкции многих переменных, к дизъюнкции применимы переместительный и сочетательный законы булевой алгебры. И следствием этого является логическая равнозначность входов у логических элементов ИЛИ, а также возможность построения многовходовых элементов ИЛИ из аналогичных элементов, но с меньшим числом входов. Если на рис.1.5 все элементы И заменить двухвходовыми элементами ИЛИ (2ИЛИ), то все выводы, сделанные относительно схем рис.1.5, будут справедливыми для схем, полученных такой заменой. Можно так же записать логико-математические модели для полученных схем и УГО элемента 6ИЛИ, заменив в выражениях (1.7), (1.8) и (1.9) все символы логического умножения знаками + (дизъюнкции).
В различных сериях ИМС имеются логические элементы ИЛИ. Например, в серии ТТЛ это микросхема К155ЛЛ1, она содержит 4 элемента 2ИЛИ.
1.3.7. Логические элементы И-НЕ
Эти элементы реализуют инверсию логического произведения
входных сигналов. Другими словами, элементы И-НЕ описываются функцией «отрицания конъюнкции». В булевой алгебре такие функции называются функциями Шеффера, для их обозначения введён специальный символ « ∕ », называемый штрихом Шеффера. Для простоты чтения мы будем использовать для обозначения функций Шеффера символ инверсии (черта вверху) над выражением конъюнкции переменных. Например, алгебраическая форма записи функции Шеффера от двух аргументов будет иметь следующий вид:
X
= a
/ b
=  = =  . (1.11) . (1.11)
В выражении (1.11) знаки равенства соответствуют логической тождественности выражений, причём правая часть выражения соответствует КСНФ функции И-НЕ (функция V13
в табл.1.3). А в целом выражение читается так: «инверсия логического произведения равна логической сумме инверсий аргументов
». Это высказывание известно в булевой алгебре как закон де Моргана
относительно инверсии логического произведения
(инверсии конъюнкции).
На рис.1.7 приведены условные графические обозначения элемента 2И-НЕ, его функциональная эквивалентная схема и карта Карно для рассматриваемой функции. Сравнивая карты Карно функций И и функций И-НЕ, нетрудно заметить, что в клетках стоят противоположные значения названных функций. Сопоставляя карты с алгебраическими выражениями функции И и функции И-НЕ, можно сделать следующие выводы:
1. Каждой единице
, стоящей в клетке матрицы, соответствует
логическое произведение
(конъюнкция) всех аргументов
функции; взятых один раз со знаком либо без знака инверсии. Если клетка с единицей располагается на области единичных значений аргумента
, то этот аргумент входит
в конъюнкцию без инверсии
. Если же клетка располагается на области нулевых значений аргумента
, то этот аргумент входит со знаком инверсии
.
2. Каждому нулю
, стоящему в клетке матрицы, соответствует логическая сумма
(дизъюнкция) всех аргументов функции, взятых один раз со знаком либо без знака инверсии. Если клетка с нулём располагается на области единичных значений аргумента
, то этот аргумент входит
в дизъюнкцию со знаком инверсии
. Если же клетка располагается на области нулевых значений аргумента
, то этот аргумент входит без знака инверсии
.
Эти выводы носят характер правил отыскания ДСНФ (первый вывод) и КСНФ (второй вывод) по булевым матрицам логических функций. Следует только добавить, что для отыскания
ДСНФ
функции необходимо эти элементарные конъюнкции
«соединять» символами дизъюнкции
(плюс), а при отыскании КСНФ
функции элементарных дизъюнкций
следует соединять символами конъюнкции
.
Под элементарной конъюнкцией
логических функций понимают логическое произведение всех аргументов функции, взятых один раз со знаком либо без знака инверсии
.
Под элементарной дизъюнкцией
логических функций понимают логическую сумму всех аргументов функции, взятых один раз со знаком либо без знака инверсии
.В сериях микросхем есть элементы И-НЕ, различающиеся числом входов, количеством элементов в одной микросхеме, а также способом организации выхода. Например, микросхема К155ЛА3 содержит 4 элемента 2И-НЕ со стандартной нагрузочной способностью. Микросхема К155ЛА8 содержит один элемент 8И-НЕ с повышенной нагрузочной способностью (она равна 30, а стандартная нагрузочная способность равна 10).
Элемент 2И-НЕ является базовым для микросхем транзисторно-транзисторной логики (ТТЛ), т.е. этот элемент положен в основу построения всех названных микросхем и в том числе микросхем ТТЛш.
1.3.8. Элементы ИЛИ-НЕ
Функции, описывающие элемент 2ИЛИ-НЕ, в булевой алгебре называют функциями Пирса, для них введён специальный символ ¯ (стрелка Пирса). В технических приложениях эти функции называют «инверсией логической суммы (дизъюнкции)» или просто функциями ИЛИ-НЕ. В частности, двухместная функция Пирса, функция 2ИЛИ-НЕ имеет следующие алгебраические выражения:
Z
= a
¯b
=  = =  . (1.12) . (1.12)
В дальнейшем эти функции будем обозначать символом инверсии над выражением логической суммы. Правая часть выражения (1.12) соответствует утверждению, что «инверсия логической суммы есть
в то же самое время логическое произведение слагаемых
, взятых с противоположными символами инверсии
». Это утверждение является вторым законом де Моргана
относительно инверсии дизъюнкции. Согласно выражению (1.12), элемент 2ИЛИ-НЕ можно представить условными графическими обозначениями при соглашениях положительной логики, при соглашениях отрицательной логики и функциональной эквивалентной схемой (рис.1.8).В интегральном исполнении выпускаются логические элементы ИЛИ-НЕ с различным числом входов. Примером может служить микросхема К155ЛЕ1, содержащая 4 логических элементов 2ИЛИ-НЕ, или К155ЛЕ3 с двумя элементами 4ИЛИ-НЕ. Как и у элементов ИЛИ, так и у элементов ИЛИ-НЕ все входы логически равнозначны.
1.3.9. Элементы «ЗАПРЕТ»
 Эти двухвходовые элементы получили такое название потому, что сигнал по одному из входов «запрещает» либо «разрешает» прохождение на выход элемента сигнала, поданного на второй вход. Поэтому один вход называется входом запрета - он инверсный, а второй вход называют «информационным». Значения выходного сигнала совпадают со значениями входного информационного сигнала в состоянии разрешения, а в состоянии запрета выходной сигнал имеет значение лог.0 независимо от значения сигнала по информационному входу. В табл.1.3 показаны две функции запрета V1
(запрет b
) и функция V4
(запрет а
). На рис. 1.9 приведены УГО элемента «запрет а
» (запрет по а
), алгебраическое выражение и карта Карно функции с аналогичным названием и функциональная эквивалентная схема элемента. Эти двухвходовые элементы получили такое название потому, что сигнал по одному из входов «запрещает» либо «разрешает» прохождение на выход элемента сигнала, поданного на второй вход. Поэтому один вход называется входом запрета - он инверсный, а второй вход называют «информационным». Значения выходного сигнала совпадают со значениями входного информационного сигнала в состоянии разрешения, а в состоянии запрета выходной сигнал имеет значение лог.0 независимо от значения сигнала по информационному входу. В табл.1.3 показаны две функции запрета V1
(запрет b
) и функция V4
(запрет а
). На рис. 1.9 приведены УГО элемента «запрет а
» (запрет по а
), алгебраическое выражение и карта Карно функции с аналогичным названием и функциональная эквивалентная схема элемента.

При а
= 0 значения функции Z
совпадают со значением аргумента b
.
Если а
= 1 (состояние запрета) на выходе элемента будет постоянно сигнал лог.0. Таким образом, вход а
является входом запрета, а вход b
- информационным. Очевидно, такое же УГО будет соответствовать элементу «запрет b
» только вход b
будет инверсным, а вход а
будет прямым. Аналогично в алгебраическом выражении такой функции аргумент b
будет со знаком инверсии, аргумент же а
войдёт без знака инверсии.
Следует отметить, что у элементов ЗАПРЕТ входы логически неравнозначны. Это в свою очередь означает, что сигналы по входам нельзя менять «местами».
Логические элементы ЗАПРЕТ выпускаются в интегральном исполнении, но не во всех сериях. Например, в серии К161 (на МОП-транзисторах с р
-каналом) есть микросхема К161ЛП2, содержащая 4 элемента ЗАПРЕТ с общим входом запрета. На рис.1.9,а
приведено условное графическое обозначение (УГО), соответствующее соглашениям положительной логики. Можно составить УГО при соглашениях отрицательной логики. Для этого над правой частью алгебраического выражения функции надо «взять» двойной знак инверсии, затем один знак раскрыть по закону де Моргана:
 = =  . (1.13) . (1.13)
Таким образом, при соглашениях отрицательной логики аналог УГО элемента ЗАПРЕТ будет представлять собой УГО элемента 2ИЛИ-НЕ, только по одному из входов следует поставить указатель инверсии.
1.3.10. Логические элементы «сумматоры по mod2» и
схемы контроля чётности /нечётности
Логическая функция V5
«неравнозначность» (табл.1.3) принимает значение лог.1 только тогда, когда нечётное число аргументов
принимают значение лог.1
. Поскольку функции и аргументы могут принимать только два значения, то эта функция равносильна операции сложения по модулю два (mod2) над двоичными числами, отображающими двоичные наборы значений аргументов. Для обозначения этой операции используется символ Å между аргументами. Эти функции, как минимум двухместные, однако, могут быть многоместными, т.е. зависеть от большего числа аргументов.
Алгебраические формы записи функции сложения по mod2 от двух аргументов имеют следующий вид:
Y
= a
Åb
=  . (1.14) . (1.14)
Правые части выражения (1.14) представляют собой ДСНФ и КСНФ, соответственно. В соответствии с этими формами можно построить функциональные эквивалентные схемы сумматора по mod2 с двумя входами. Эти схемы, а также УГО, рекомендованное ГОСТом, и булева матрица этой функции приведены на рис.1.10.
Обратите внимание, в схеме рис.1.10,а
использованы УГО элементов запрета и элемент 2ИЛИ. В схеме рис.1.10,в
для реализации дизъюнкции инверсий аргументов применён элемент 2И-НЕ и, кроме того, элементы 2ИЛИ и 2И. Приведённые схемы лишний раз показывают, что функциональных схем для двухвходового сумматора по mod2 можно составить несколько!Выше, на рис.1.2,а
, в качестве примера была приведена карта Карно 4-местной функции сложения по mod2. Она может быть реализована 4-входовым сумматором по mod2 с условным графическим обозначением, аналогичным рис.1.10,г
(должно быть 4 входа).
Так как от перемены мест слагаемых сумма по mod2 не меняется, то все входы у сумматоров по mod2 логически равнозначны. Заметим ещё раз! Что если число входных сигналов, принявших значение лог.1, чётное, то выходной сигнал сумматора по mod2 будет равен лог.0, т.е. имеет неактивное значение, - чётность «не нарушена». Поэтому такие элементы получили название «схем контроля чётности».
Обратите теперь внимание на функцию V
10
- функцию логической равнозначности
, (табл.1.3). Она принимает противоположные значения по сравнению с суммой по mod2, то есть является её инверсией. Поэтому условное графическое обозначение элемента, её реализующего, будет отличаться от рис.1.10,г
лишь наличием указателя инверсии на выходе элемента.
Используя алгебраические выражения двухместной функции равнозначности (1.15), можно получить функциональные эквивалентные схемы двухвходового сумматора по mod2 с инверсным выходом (2Å-НЕ).
X
=  = =  = =  . (1.15) . (1.15)
Карта Карно этой функции будет отличаться от карты рис.1.10,б
тем, что в клетки следует ставить противоположные значения (нули заменить единицами, а единицы − нулями). Нетрудно установить смысловое значение этой функции, поскольку она принимает значение лог.1 при чётном числе и значение лог.0 при нечётном
числе единичных значений её аргументов. Схемы же её реализующие получили название «схем контроля нечётности
».
  В интегральном исполнении выпускаются логические элементы 2Å, например, микросхема К155ЛП5 содержит 4 таких элемента. В интегральном исполнении выпускаются логические элементы 2Å, например, микросхема К155ЛП5 содержит 4 таких элемента.
Есть микросхемы, выполняющие функцию многовходового сумматора по mod2 с прямым и инверсным выходом. Например, микросхема К155ИП2 является 8-разрядной схемой контроля чётности/ нечётности
с прямым и инверсным выходом и с двумя управляющими входами. Такой микросхемой реализуются одновременно функция 8Å и функция 8Å-НЕ. Условное графическое обозначение этой микросхемы и таблица, описывающая режимы работы ИМС, приведены на рис.1.11.
В табл.1.4, в столбцах значений выходных сигналов X
и Y
, приведены сокращённые алгебраические выражения одноимённых выходных функций. Из этих выражений следует, что при комбинации сигналов на управляющих входах v
1
=0 и v
2
=1 на выходе X
будет реализована сумма по mod2 всех восьми информационных сигналов. В то же самое время на выходе Y
будет реализована инверсия этой суммы. Кроме того, из таблицы видно, что при комбинациях сигналов на управляющих входах 0-0 либо 1-1 микросхема оказывается в «нерабочем» состоянии, когда на обоих выходах сигналы принимают одинаковые значения независимо от значений входных информационных сигналов.
1.3.11. Мажоритарные логические элементы
Эти элементы описываются логическими функциями, у которых число аргументов больше двух и является нечётным
. Соответственно у любого мажоритарного элемента число входов всегда нечётное
. Выходной сигнал принимает активное значение, когда большинство входных сигналов
принимают активные значения. Поэтому такими элементами реализуется «принцип большинства
» в обработке или в приёме сигналов.
Допустим, что за активное значение входных и выходного сигналов принят уровень лог.1. Тогда у мажоритарного элемента «³ 2 из 3-х» (с тремя входами) сигнал на выходе будет равен лог.1, если два (любых) либо все три входных сигнала принимают значение лог.1.
На рис.1.12 приведены УГО такого элемента, карта Карно выходной функции и функциональная его эквивалентная схема.
По карте функции F
можно найти её минимальную дизъюнктивную нормальную форму (МДНФ):
F
= ab
+ bc
+ ac
. (1.16)
Этой формулой непосредственно описывается схема рис.1.12,б
. Как видно по карте Карно (рис.1.12,в
), единицы стоят в клетках, расположенных на областях единичных значений двух и всех трёх аргументов. По аналогии можно построить карту Карно для мажоритарного элемента «³3 из 5-ти», найти минимальное алгебраическое выражение его выходной функции, а затем построить функциональную схему.
В интегральном исполнении мажоритарные элементы есть, но не во всех сериях. Например, в серии КР1533 есть микросхема КР1533ЛП3, представляющая собой три мажоритарных элемента «³2 из 3-х» с инверсным общим входом управления. Сигнал лог.0 по входу управления разрешает выполнение функций мажоритарности, а сигнал лог.1 запрещает их реализацию. Функциональная схема этой микросхемы и её УГО приведены на рис.1.13. Сопоставляя функциональную схему рис.1.13,б
со схемой мажоритарного элемента рис.1.12,б
, можно понять, как организовано управление, и какие значения принимают выходные сигналы при подаче на управляющий вход (он помечен на УГО меткой «Е») сигнала лог.1. (На УГО и соответственно на схеме рис.1.13,б
цифры означают номера выводов микросхемы.)
 |
 |
Есть мажоритарные элементы с инверсным выходом, например, микросхемы 533ЛП3 и КР134ЛП3 содержат по три таких элемента. В этом случае принцип «большинства» будет реализован относительно сигналов низкого уровня (сигналов лог.0). Следует также заметить, у мажоритарных элементов, как и у элементов И-НЕ и ИЛИ-НЕ, все входы логически равнозначны, т.е. порядок подачи входных сигналов не имеет существенного значения.
1.3.12. Элементы «логического порога» и элементы
«исключающее ИЛИ»
Среди многовходовых логических элементов можно выделить группу элементов, у которых выходной сигнал принимает активное значение только в тех случаях, когда определённое заданное число входных сигналов также принимают активное значение. Такие элементы принято называть элементами «логического порога». В частности, если выходной сигнал
принимает значение лог.1
, когда только один и только один
из входных сигналов принимает значение лог.1, то такие элементы называют элементами «исключающее ИЛИ». Это тоже элементы логического порога, только «порог» равен единице. Для них ГОСТами также регламентировано УГО, в основное поле которого помещается метка «=1» (для элементов исключающее
ИЛИ), либо метка вида «=n
», где n
целое число меньше числа входов у логического элемента.
Так, на рис.1.14 приведены УГО элемента исключающее
ИЛИ с тремя входами, УГО элемента логического порога «=2 из 4-х», карты Карно их выходных функций и функциональные эквивалентные схемы.
Анализируя приведённые карты Карно функций X
и Y
, замечаем, что
минимальных дизъюнктивных алгебраических форм у этих функций нет (о визуально-матричном способе минимизации логических функций будет сказано ниже).Поэтому функциональные схемы названных элементов можно построить, найдя алгебраические выражения в ДСНФ либо в других формах.Так, схема рис.1.14,д
получена по следующему выражению:
X
=  . (1.17) . (1.17)Это ДСНФ функции «исключающее ИЛИ». Если бы аналогично находить выражение функции Y
, то оно состояло бы из 6 дизъюнктивных членов (слагаемых), каждый из которых представлял бы произведение всех 4-х аргументов. Тогда функциональная схема элемента логического порога «=2 из 4-х» состояла бы из элемента 6ИЛИ, шести логических элементов 4И и из 4-х элементов НЕ. Схема же на рис.1.14,е
получена по следующему логическому выражению:
Y
= (a
Åd
)(b
Åc
) + (a
Åb
)(c
Åd
). (1.18)
О правилах получения подобного рода алгебраических выражений по булевым матрицам логических функций речь будет идти ниже. Сейчас же уместно напомнить, что сумма по mod2 отображается на картах Карно шахматным узором расположения единиц и нулей. Так, выражение (1.18) получено по выделенным различной заливкой «частным шахматным узорам» (рис.1.14,г
) для функции Y
с применением операции выноса за скобки общих сомножителей. Аналогичное выражение можно было бы получить и для функции «исключающее ИЛИ» по карте рис.1.14,б
.
Следует отметить, что в частном случае, когда число входов у элемента «исключающее ИЛИ» равно двум, то эта функция тожественно равна функции сложения по mod2 от двух аргументов (2Å). К сожалению, в интегральном исполнении логические элементы «исключающее ИЛИ» и «логического порога» при числе входов более двух не выпускаются.
1.3.13. Логические элементы «ИМПЛИКАТОРЫ»
Эти логические элементы описываются функцией «импликация» (табл.1.3 функции V
11
и V
14
).
 V
11
= b
®a
= V
11
= b
®a
=  , ,
V
14
= a
®b
=  . (1.19) . (1.19)
Первая из функций называется «импликация b
», а вторая - «импликация а
». На рис.1.15 приведены условные графические обозначения логического элемента ИМПЛИКАТОР а
и карта Карно его выходной функции. Правые части выражений (1.19) свидетельствуют о том, что функция импликации в то же самое время является инверсией функции ЗАПРЕТ.
Из карты рис.1.15,в
следует, что функция импликации ложна
только в том случае, когда один
из аргументов принимает ложное значение
, а другой -истинное
.
  В интегральном исполнении ИМПЛИКАТОРЫ в сериях ИМС широкого применения практически не выпускаются. Вместе с тем, согласно УГО рис.1.15,а
и в,
функцию импликации можно реализовать элементом 2ИЛИ, подав сигнал на его один из входов через инвертор, либо - на элементе ЗАПРЕТ, включив на его выход инвертор. Эти функциональные эквивалентные схемы мы не приводим, из-за их тривиальности. В интегральном исполнении ИМПЛИКАТОРЫ в сериях ИМС широкого применения практически не выпускаются. Вместе с тем, согласно УГО рис.1.15,а
и в,
функцию импликации можно реализовать элементом 2ИЛИ, подав сигнал на его один из входов через инвертор, либо - на элементе ЗАПРЕТ, включив на его выход инвертор. Эти функциональные эквивалентные схемы мы не приводим, из-за их тривиальности.
Следует отметить, что входы у логических элементов импликаторов логически неравнозначны
, поэтому порядок подачи входных сигналов строго фиксирован.
1.3.14. Многофункциональные логические элементы
Выше были рассмотрены «простые
» логические элементы, которые реализуют простые либо достаточно простые
логические операции. Вместе с тем, в интегральном исполнении выпускаются более сложные логические элементы (ЛЭ), которые способны реализовать (одновременно, либо путём перекоммутации входов к шинам лог.0 или лог.1) несколько простых функций. По сути, эти элементы допускают возможность реализации многоместных логических функций по фрагментам их нормальных дизъюнктивных, либо нормальных конъюнктивных алгебраических форм. В табл.1.2 уже были приведены названия интегральных схем по функциональному назначению и их условные обозначения. Рассмотрим только наиболее широко применяемые многофункциональные ЛЭ.
Логические элементы И-ИЛИ-НЕ
Такие элементы реализуютинверсию
дизъюнктивных нормальных форм
(ДНФ) алгебраических выражений функций, что эквивалентно реализации конъюнктивных нормальных форм
(КНФ) этих функций. Так, на рис.1.16 приведены УГО микросхем К155ЛР1 и К155ЛР3. В микросхеме К155ЛР1 содержится два элемента 2-2И-2ИЛИ-НЕ, а микросхема К155ЛР3 представляет собой один элемент 2-2-2-3И-4ИЛИ-НЕ, расширяемый по ИЛИ.
По функциональной схеме (рис.1.16,б
) одного из элементов микросхемы К155ЛР1 можно составить следующее алгебраическое выражение его выходной функции:F
=  = =  . (1.20) . (1.20)
Таким образом, эта функция от 4-х аргументов, причём правая часть выражения (1.20) соответствует минимальной конъюнктивной нормальной форме функции F
(МКНФ). Левая часть этого выражения непосредственно соответствует УГО элемента 2-2И-2ИЛИ-НЕ. Второй такой же элемент этой микросхемы имеет «нелогические» входы расширения по ИЛИ. Они помечены в левом дополнительном поле УГО метками «э» - эмиттера вывод и «к» - коллектора вывод. Нелогическими
выводами (входы либо выходы) принято называть такие, на которых сигналы могут принимать значения нестандартных уровней
напряжения. Такие выводы помечаются на УГО логических элементов (либо микросхем) специальным указателем в виде «крестика» ´. В частности, у рассматриваемых ИМС эти выводы выполнены от коллектора и эмиттера транзистора фазорасщепляющего каскада базового логического элемента серий ИМС ТТЛ. Подключая к ним выходы соответствующих ИМС «расширителей по ИЛИ», можно наращивать число входов элемента ИЛИ-НЕ, входящего в состав многофункционального элемента. Например, для рассматриваемых микросхем коэффициент объединения по входу равен 8, а расширители по ИЛИ реализуют логическое произведение нескольких входных сигналов. По существу расширители по ИЛИ являются многовходовыми элементами И с той лишь разницей, что выходные сигналы не имеют стандартных уровней лог.0 и лог.1. Отмеченное позволяет записать по аналогии с выражением (1.20) алгебраическое выражение выходной функции V
для второго элемента:
V
=  . (1.21) . (1.21)
Максимальное число последующих слагаемых в выражении (1.21) может быть равным 8 (в соответствии с коэффициентом объединения по входам), а каждое слагаемое может быть отображено конъюнкцией максимально от восьми аргументов. Таким образом, выражения (1.20) и (1.21) определяют логико-математическую модель микросхемы К155ЛР1.
Предлагаем Вам самостоятельно найти логико-математическую модель микросхемы К155ЛР3, используя для этого показанное на рис.1.16,г
её условное графическое обозначение.
Логические элементы ИЛИ-И
Эти логические элементы реализуют фрагменты конъюнктивных нормальных форм (КНФ) булевых функций, то есть логическое произведение логических сумм от нескольких аргументов. Например, самым простым будет элемент 2-2ИЛИ-2И. Такой элемент описывается функцией вида
X
= (a
+ b
)(c
+ d
). (1.22)
На рис.1.17 приведено УГО этого элемента, карта Карно его выходной функции X
и функциональная эквивалентная схема.
В интегральном исполнении выпускаются подобные ЛЭ, например, в серии ИМС ЭСЛ есть микросхема К500ЛС118, представляющая собой два логических элемента 2-3ИЛИ-2И с одним общим входом. На рис.1.17,г
показано УГО этой микросхемы. По условному её графическому обозначению можно составить следующие логические выражения выходных функций Y
и Z
:
 Y
= (x
1
+ x
2
+ x
3
)(x
4
+ x
5
+ x
6
), (1.23) Y
= (x
1
+ x
2
+ x
3
)(x
4
+ x
5
+ x
6
), (1.23)
Z
= (x
6
+ x
7
+ x
8
)(x
9
+ x
10
+x
11
).
Выражения (1.23) являются логико-математической моделью рассматриваемой микросхемы. Наличие общего входа x
6
даёт возможность использовать микросхему К500ЛС118 в качестве двух независимых элементов вида 2-3ИЛИ-2И (при x
6
=0),
либо в качестве двух независимых элементов 3ИЛИ (при x
6
=1). В этом легко убедиться, подставив соответствующие значения x
6
в выражения (1.23).
Логические элементы ИЛИ-НЕ / ИЛИ
По существу, эти элементы являются элементами ИЛИ с двумя выходами - прямым и инверсным. Поэтому они реализуют одновременно дизъюнкцию и инверсию дизъюнкции от одного и того же множества входных сигналов и описываются одноимёнными логическими функциями. Так на рис.1.18,а
показано УГО элемента 3ИЛИ-НЕ / 3ИЛИ и условные графические обозначения микросхем серии К500, содержащих подобные логические элементы. На рисунке также приведены карты Карно выходных функций указанного элемента, функциональная эквивалентная его схема (рис.1.18,б
) и УГО микросхем К500ЛМ105 (рис.18,д
), К500ЛМ109 (рис.1.18,е
) и К500ЛМ101 (рис.1.18,ж
). Следует отметить, приведённый вариант функциональной схемы не единственный - вместо элемента 3ИЛИ-НЕ может быть использован элемент 3ИЛИ и также элемент НЕ. По условным графическим обозначениям перечисленных микросхем нетрудно уяснить, что ИМС К500ЛМ105 содержит три независимых элемента: два элемента 2ИЛИ-НЕ/ 2ИЛИ и один элемент 3ИЛИ-НЕ /3ИЛИ.
 Аналогично можно уяснить состав микросхемы К500ЛМ109 Аналогично можно уяснить состав микросхемы К500ЛМ109

(рис.1.18,е
).
Обратите внимание на УГО микросхемы К500ЛМ101(рис.1.18,ж
). Микросхема содержит 4 однотипных элементов типа 2ИЛИ-НЕ /2ИЛИ с раздельными выходами и с одним общим входом х
5
. Если сигнал по этому входу х
5
= 0, то микросхему можно рассматривать как набор из 4-х элементов НЕ и, в то же самое время, как набор из четырёх повторителей сигналов по входам х
1
, х
2
, х
3
и х
4
. Если же х
5
= 1, то независимо от значений других входных сигналов на прямых выходах установятся сигналы лог.1, а на инверсных выходах сигналы лог.0. Таким образом, каждый элемент в микросхеме играет роль управляемого инвертора-повторителя
.
Дополнительно отметим, что в серии К500 имеются логические элементы вида ИЛИ-И-НЕ/ИЛИ-И, например микросхема К500ЛК117. Это - практически, аналог микросхемы К500ЛС118 (рис.1.17,г
) с тем отличием, что каждый элемент 2-2ИЛИ-2И имеет прямой и инверсный выходы.
Мы рассмотрели практически все широко используемые при построении цифровых устройств логические элементы. Анализируя изложенный материал, можно придти к следующим выводам:
1. Существует возможность однозначного перехода
от
аналитического описания
ЛЭ к его условному графическому обозначению
либо к функциональной
эквивалентной его схеме.
2. Существует возможность однозначного перехода
от УГО
элемента либо от его функциональной схемы
к аналитическому его описанию
. При этом функционирование элемента описывается алгебраическими выражениями логических функций, реализуемых элементом.
3. Функциональные схемы сложных ЛЭ можно построить на различных
более простых (менее сложных) логических элементах
, причём существует неоднозначность
(многовариантность) построения функциональных эквивалентных схем для одного и того же ЛЭ.
Поскольку логические устройства по существу представляют собой совокупность взаимосвязанных логических элементов, то сформулированные выводы
можно с успехом распространить и на устройства
.
Вместе с тем возникает проблема
, - каким образом можно построить устройство
с минимальным количеством
ЛЭ и на элементах минимальной номенклатуры
. Другими словами, как построить устройство с минимальными аппаратурными затратами
.
Решение
этой проблемы
основывается на знании функционально полных наборов логических элементов
и выборе по определённым критериям соответствующего набора
.
1.3.15. Функционально полные наборы логических элементов
Функционально полным
называется такой набор
ЛЭ, на которых (из которых) можно построить любое логическое устройство
сколь сложно оно ни было бы. Функциональная полнота
некоторого набора логических элементов, в свою очередь, определяется полнотой
некоторой системы логических функций
, которые являются логико-математическими моделями выбранного набора ЛЭ.
В булевой алгебре существует теорема Поста-Яблонского
, согласно которой устанавливаются критерии полноты
некоторой системы логических функций
. Сущность этой теоремы сводится к следующему.
Некоторая система логических функций будет полной, если она содержит:
а) функцию, не сохраняющую логическую константу
0,
f
(x
1
, x
2
, ¼x
n
) = f
(0, 0, ¼0) ¹ 0;
б)функцию, не сохраняющую логическую константу
1,
f
(x
1
, x
2
, ¼x
n
) = f
(1, 1, ¼1) ¹ 1;
в) функцию, не являющуюся самодвойственной
,
 ¹ ¹ ; ;
г) функцию, не являющуюся линейной
,
f
(x
1
, x
2
, ¼x
n
) ¹х
1
Åх
2
żÅх
n
Åх
1
х
2
żÅх
1
х
2
¼x
n
;
д) функцию, не являющуюся монотонной
.
Если Х1
есть некоторый фиксированный набор значений аргументов функции f
(x
1
,x
2
,x
3,
x
4
), например Х1
= <x
1
, x
2
, x
3,
x
4
> = <1,1,0,1>, а Х2
= <x
1
, x
2
, x
3,
x
4
> = <0,0,0,1> - другой набор этих аргументов, то можно считать, что Х1
> Х2
, т.е. набор Х2
меньше набора Х1
.
|