МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
РАДИОЭЛЕКТРОНИКИ
Кафедра ПЭЭА
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОМУ ПРОЕКТУ
По дисциплине: “Элементная база ЭА”
Тема: “Экранированная катушка индуктивности:
рабочая частота – 5 МГц; индуктивность - 20 мкГн”
Выполнил: Руководитель:
ст. гр. ВЕЗз
– 05 – 1 Григорьева О.В.
Александров Д. В.
2008
СОДЕРЖАНИЕ
Введение
1. Анализ технического задания
2. Обзор аналогичных конструкций и выбор направления проектирования
3. Расчет конструкции и необходимых деталей
3.1 Выбор материала и обоснование конструкции
3.2 Расчет числа витков
3.2.1 Определение фактической длины намотки
3.2.2 Расчет оптимального диаметра провода
3.3 Уточнение электрических параметров конструкции
3.4 Экранирование катушки
3.5 Определение температурного коэффициента индуктивности
4. Описание конструкции
Выводы
Список литературы
ВВЕДЕНИЕ
Катушка индуктивности является элементом радиоэлектронных средств, функционирование которой определяется эффектом перехода энергии электрического поля в энергию магнитного поля вследствие протекания по контуру катушки электрического тока. Величина индуктивности определяется конструкцией токопровода и его размерами.
В производстве электронной техники применяются различные конструкции катушек индуктивности, в зависимости от требований предъявляемым к изделию. Различают катушки индуктивности избирательных и апериодических цепей. Катушки индуктивности избирательных цепей входят в состав фильтров, линий задержки, колебательных контуров, катушек связи, дросселей высокой частоты и т. п. Катушки индуктивности апериодических цепей являются составными узлами различных трансформаторов и дросселей низкой частоты.
Различают катушки постоянной и переменной индуктивности. Катушки с большими изменениями индуктивности являются вариометрами, а с малыми изменениями индуктивности (10-15%) – подстроенными.
По конструктивному исполнению катушки делятся на цилиндрические и плоские. Цилиндрические катушки индуктивности бывают каркасные и бескаркасные (обладающие большей добротностью).
Различают катушки индуктивности с однослойной и многослойной намоткой. Многослойные катушки менее технологичны и менее надежны. Различают также экранированные и неэкранированные катушки индуктивности.
В катушках индуктивности применяют магнитные и немагнитные сердечники характер, которого влияет на добротность катушки и интервал варьирования величины индуктивности.
Перспектива развития катушек индуктивности связаны с разработкой новых материалов, имеющие высокие магнитные проницаемости и стабильность на радиочастотах, превосходящие по своим свойствам ферриты, а также развитием конструкции и технологии изготовления таких изделий.
1. АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ
Согласно технического задания необходимо спроектировать экранированную катушку индуктивности :
Рабочая частота – 5 МГц
L = 20 мкГн
Для обеспечения стабильности катушки индуктивности в указанных условиях эксплуатации, а именно: В 3.1 по ГОСТ 15150-69, всеклиматическое исполнение подразумевает рабочий интервал температур от +45 до -10°С необходимо чтобы температурный коэфициент индуктивности был минимален.
При заданной величине индуктивности, равной 20 мкГн, целесообразно применить однослойную намотку медным обмоточным проводом типа ПЭВ -2 (ГОСТ 16186-74) на каркас цилиндрической формы из полистирола, имеющим небольшой температурным коэффициент расширения для обеспечения малого температурного коэффициента индуктивности.
В данной конструкции необходимо применить сердечник из карбонильного железа P-100, в качестве подстройки, т. к. экранирование повлечёт некоторое изменение индуктивности.
Для обеспечения годовой программы выпуска, равной 1000 штук, необходимо сравнительно невысокая технологичность, но количество операций по сборке катушки индуктивности должно быть оптимальным.
2. ОБЗОР АНАЛОГИЧНЫХ КОНСТРУКЦИЙ
Величина индуктивности промышленных катушек индуктивности колеблется в пределах от сотых долей до сотен микрогенри. Должна обеспечиваться точность в пределах 0,3...0,5%. На практике применяются катушки индуктивности цилиндрические и кольцевые. Для обеспечения высокой добротности в качестве каркаса используется керамика. Конструктивно керамические катушки представляют собой цилиндр на который наносится обмотка. В настоящее время применяются катушки индуктивности с каркасами из вакуумной керамики. Для уменьшения ТКИ и диэлектрических потерь каркасы имеют ребристую поверхность. Материалом для каркасов служит керамика и пресс- материал ДСВ-2Р-2М. Используются каркасы диаметром от 10...30 мм.
Катушки на керамических каркасах изготавливают тремя способами:
1) на каркас наматывают с натяжением медный провод;
2) на горячий каркас наматывают с натяжением медную ленту;
3) на каркас наносят воженное серебро в виде витков обмотки и покрывают их гальвано способом слоем меди.
Практически величина добротности находится в пределах 100...1000, лучшая добротность однослойных цилиндрических катушек достигается при 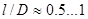 . Величина добротности зависит от частоты, геометрических размеров и конструкции, числа витков и типа провода. Так, на частотах до . Величина добротности зависит от частоты, геометрических размеров и конструкции, числа витков и типа провода. Так, на частотах до  3...4 МГц преимущественно следует использовать провод типа литцендрат (ЛЭШО, ЛЭЛО, ЛЭВ, ЛЭТ), так как это позволяет получить более высокую добротность. При более высоких частотах применяют одножильный провод (ПЭВ, ПЭМ, ПЭЛО, ПЭЛ) 3...4 МГц преимущественно следует использовать провод типа литцендрат (ЛЭШО, ЛЭЛО, ЛЭВ, ЛЭТ), так как это позволяет получить более высокую добротность. При более высоких частотах применяют одножильный провод (ПЭВ, ПЭМ, ПЭЛО, ПЭЛ)
Добротность катушек на кольцевых каркасах относительно меньше, чем у таких же катушек на цилиндрических каркасах.
3. ЭЛЕКТРИЧЕСКИЙ И КОНСТРУКТОРСКИЙ РАСЧЕТ КАТУШКИ ИНДУКТИВНОСТИ
Создание оптимальной катушки индуктивности является довольно сложной задачей из-за противоречивого характера предъявляемых к ним требованиям и состоит в следующем:
1) выбор материала и обоснование конструкции;
2) расчета числа витков;
3) определение конструктивных размеров и уточнение электрических параметров конструкции.
3.1 Выбор материала и обоснование конструкции
Материал, из которого изготовлена обмотка катушки индуктивности, должен обладать низким удельным сопротивлением и сравнительно не большим коэффициентом линейного расширения. Наиболее полно этим требованиям удовлетворяет медь имея:
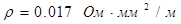 ; ;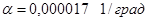 . .
Намотку следует осуществлять проводом типа ПЭВ, так как он применяется на высоких частотах. Примем к расчету следующий провод:
ПЭВ-2 ГОСТ 16186 – 74.
Данный тип провода выбран из следующих соображений; при увеличении частоты глубина проникновения токов уменьшается, этот процесс, для средней частоты рабочего диапазона равный 5 МГц, можно описать как
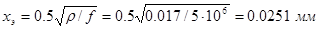 , ,
отсюда следует, что нет смысла для данного рабочего диапазона использовать провод большего диаметра.
В качестве материала каркаса используем полистирол диаметром 10мм.
Конструкция катушки индуктивности определяется назначением и условиями эксплуатации. Так для данной катушки индуктивности (данные которой приведены в техническом задании) нужно указать ряд конструктивных решений:
1) выполнить обмотку на каркасе с сердечником – это даст возможность подстройки величины индуктивности, в зависимости от того магнитный или немагнитный сердечник величина добротности увеличится либо уменьшится;
2) выполнить экранирование катушки индуктивности – это конструктивное решение снизит влияние внешних полей, уменьшит добротность.
3.2 Расчет числа витков
Расчет числа витков и определение размеров катушки с цилиндрическим сердечником произвели по формулам, применяемым для расчёта катушки без сердечника. Обеспечили подстройку индуктивности (номинальная – 20 мкГн) на  5%. 5%.
Приняли расчетную индуктивность равную 21 мкГн.
Расчет числа витков однослойной обмотки осуществили по методу предложенному В.А. Волговым и изложенному в [1]. Число витков можно определить, если известны диаметр и длина намотки по формуле
 , (3.1) , (3.1)
где D – диаметр обмотки (данный параметр выбираться из производственных возможностей), в см;
L – индуктивность катушки (заданная величина), в мкГн;
L0
- коэффициент формы (табличное значение).
Диаметр обмотки выбран из соображений целесообразности, а именно: диаметр обмотки катушки индуктивности будет соответствовать, внешнему диаметру стандартного сердечника из карбонильного железа Р-100.
Умножим и разделим правую часть выражения  , на , на 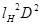 . Получим . Получим
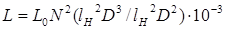 , (3.2) , (3.2)
Величину 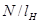 обозначим через обозначим через 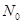 – определяет количество витков, приходящихся на единицу длины намотки, которое определяется как – определяет количество витков, приходящихся на единицу длины намотки, которое определяется как
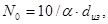 (3.3) (3.3)
где a - коэффициент не плотности намотки, определяется из условия
выбранного диаметра в изоляции;
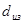 - диаметр провода в изоляции. - диаметр провода в изоляции.
Так, для выбранного провода ПЭВ - 2 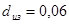 (из источника [3]), данному значению (из источника [3]), данному значению 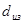 соответствует a=1,3 (из источника [1], приложение). Тогда принимая во внимание формулу (3.3) получим соответствует a=1,3 (из источника [1], приложение). Тогда принимая во внимание формулу (3.3) получим
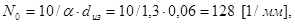 (3.4) (3.4)
Произведение 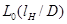 обозначим как обозначим как  – определяется соотношение длины и диаметром намотки. Учитывая принятые обозначения, получим формулу: – определяется соотношение длины и диаметром намотки. Учитывая принятые обозначения, получим формулу:
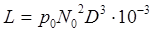 , (3.5) , (3.5)
Из формулы (3.5) следует выражение
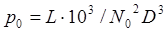 , (3.6) , (3.6)
Учитывая выражения (3.2) и (3.6) подставляя числовые значения в (3.6), получим
 (3.7) (3.7)
По графику [1] определено отношение длины намотки к диаметру намотки 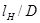 . Для данного случая оно составляет . Для данного случая оно составляет 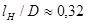 . По полученному значению определяем длину намотки как . По полученному значению определяем длину намотки как
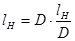 , (3.8) , (3.8)
Числено это определяется так
 (3.9) (3.9)
По известному значению длины намотки определяем число витков, используя следующее соотношение
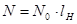 , (3.10) , (3.10)
Учитывая выражения (3.6) и (3.11) получим
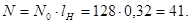 (3.11) (3.11)
3.2.1 Определение фактической длины намотки
При сплошной намотке фактическая геометрическая длина катушки определяется формулой
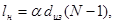 (3.12) (3.12)
числено фактическая длина будет равна
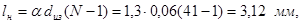 (3.13) (3.13)
(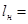 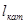 =3,12мм) =3,12мм)
По известному числу витков, определили фактическую индуктивность катушки по формуле
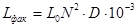 , (3.14) , (3.14)
учитывая значение, полученное из выражения (3.13), по графику зависимости 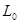 от от 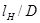 [1] получили [1] получили 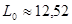 , подставляя полученное значение получили , подставляя полученное значение получили
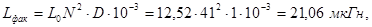 (3.15) (3.15)
Полученное значение 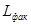 на 0,285% отличается от требуемого значения на 0,285% отличается от требуемого значения 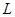 , следовательно, коррекцию количества витков можно не выполнять, т. к. полученное значение вполне допустимо. , следовательно, коррекцию количества витков можно не выполнять, т. к. полученное значение вполне допустимо.
3.2.2 Расчет оптимального диаметра провода
Расчет оптимального диаметра провода производится графоаналитическим методом:
Определяем по формуле (3.16)
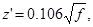 (3.16) (3.16)
где 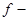 средняя частота рабочего диапазона, Гц; средняя частота рабочего диапазона, Гц;
Вспомогательный коэффициент равен:
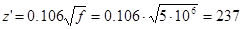
Пользуясь графиком (из источника [1], приложение А) определяем поправочный коэффициент 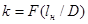 . Для . Для 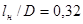 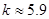
Находим вспомогательный параметр y по формуле (3.17)
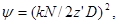 (3.17) (3.17)
где N – число витков обмотки;
k – поправочный коэффициент;
z¢– вспомогательный коэффициент;
D – диаметр каркаса, см.
Вспомогательный параметр y равен:
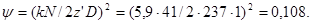 (3.18) (3.18)
при 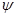 <0,3 <0,3
Определяем величину zопт
, по формуле:
zопт
= =5,01 (3.19) =5,01 (3.19)
По найденному значению zопт
находим оптимальный диаметр провода, по формуле:
 (3.20) (3.20)
Итак, оптимальный диаметр провода будет равен:
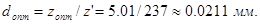
Ближайшим по значению диаметра (из выбранного типа) из стандартного ряда является: 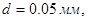 свой выбор остановим на проводе типа ПЭВ- 0,05 ГОСТ 16186 - 74. свой выбор остановим на проводе типа ПЭВ- 0,05 ГОСТ 16186 - 74.
3.3 Уточнение электрических параметров конструкции
Как, впрочем, и другие конструкции данная конструкция катушки индуктивности не совершенна из-за присутствующих сопротивлений потерь. Сопротивление потерь намотки характеризуется активным сопротивлением провода и его сопротивлением току высокой частоты. Сопротивление провода является физический характеристикой материала, из которого изготовлен данный провод, и является справочной величиной. Активное сопротивление металлического отрезка провода длиной 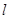 и площадью поперечного сечения и площадью поперечного сечения 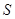 определяется по следующему соотношению определяется по следующему соотношению
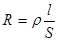 , (3.21) , (3.21)
где 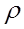 - удельное сопротивление материала, из которого изготовлен провод, для меди оно составляет 0,0017 - удельное сопротивление материала, из которого изготовлен провод, для меди оно составляет 0,0017  ; ; 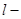 фактическая длина намотки. фактическая длина намотки.
Учитывая это, получим:
 (3.22) (3.22)
где 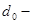 диаметр одной жилы; диаметр одной жилы; 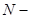 количество витков обмотки; количество витков обмотки; 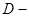 диаметр сердечника ( диаметр сердечника (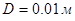 ). ).
Тогда, учитывая данные примечания, получим:
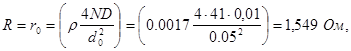
Сопротивление провода круглого диаметра току высокой частоты можно вычислили по формуле
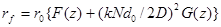 , (3.23) , (3.23)
где r0
– сопротивление постоянному току, Ом; F(z) – коэффициент, определяющий сопротивление с учетом поверхностного эффекта; G(z) – коэффициент, учитывающий эффект близости; N – количество витков намотки; D – диаметр каркаса; 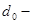 полный диаметр провода без наружной изоляции. полный диаметр провода без наружной изоляции.
Значения коэффициентов F(z) и G(z) определены из таблицы [1]
Аргумент z определяется по формуле
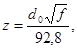 (3.24) (3.24)
где 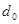 – диаметр провода, мм; – диаметр провода, мм; 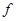 – частота Гц. – частота Гц.
И равен: 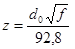 = =
При z=1,44: F(z)=1.183
G(z)=0.0369
Найдем численное значение 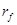 : :
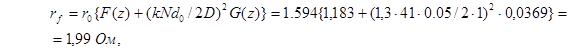
Расчет сопротивления потерь в диэлектрике каркаса
Сопротивление потерь в диэлектрике каркаса вычислим по формуле
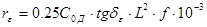 , (3.25) , (3.25)
где 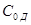 - емкость через диэлектрик, - емкость через диэлектрик, 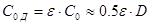 , пФ; , пФ; 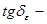 тангенс угла диэлектрических потерь, для полистирола тангенс угла диэлектрических потерь, для полистирола 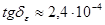 ; ; 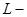 фактическая индуктивность катушки, мкГн; фактическая индуктивность катушки, мкГн; 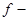 частота, МГц; ε – диэлектрическая проницаемость полистирола (ε=2,5) частота, МГц; ε – диэлектрическая проницаемость полистирола (ε=2,5)

3.4 Экранирование катушки
Осуществим экранирование катушки с помощью замкнутого экрана цилиндрической формы, изготовленный из меди. По заданным размерам каркаса катушки (Dk
, lk
) и начальной индуктивности L0
определим Dэ
(диаметр экрана) и его длину lэ
.
Исходя из условия необходимо, чтоб имело силу равенство
Dэ
- Dk
= lэ
- lk
(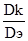 =0,45). (3.26) =0,45). (3.26)
При заданном 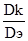 находим Dэ
, а из формулы (3.26) длину lэ находим Dэ
, а из формулы (3.26) длину lэ
Тогда Dэ
=10/0,45=22,22 мм
lэ
= Dэ
- Dk
+ lk
=22,22-10+25,73=37,95 мм
Толщину стенок экрана определим из источника (4):
t=0,1 мм
Расчет индуктивности после экранирования.
Индуктивность однослойной катушки L0
при размещении её в экране уменьшается и может быть определена по формуле:
Lэ
=L0
βL
, (3.27)
где βL
-коэффициент уменьшения индуктивности, определяемый по приближенной формуле:
βL
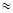 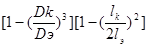 (3.28) (3.28)
Тогда
βL
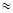 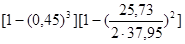 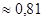
Вычислим Lэ
:
Lэ
=21,06∙0,81=17,05 мкГ
Найдем приращение индуктивности из формулы:
Lэ
= L0
-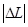 , (3.29) , (3.29)
где 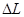 - приращение индуктивности; - приращение индуктивности; 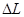 <0 <0
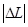 = L0
- Lэ
=21.06-17.05=4.01. = L0
- Lэ
=21.06-17.05=4.01.
Из формул (3.27) и (3.29) следует, что относительное уменьшение индуктивности составит:
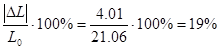
относительное изменение составило 0,19, т.е. индуктивность катушки в экране изменилось на 19%. и равна 17,05 мкГн.
Расчет сопротивления, вносимого экраном
Вносимое экраном активное сопротивление с учетом поверхностного эффекта рассчитаем по формуле:
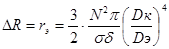 , (3.30) , (3.30)
где DЭ
– диаметр экрана цилиндрической формы, 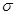 - электропроводность материала экрана, - электропроводность материала экрана, 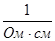 (для меди (для меди 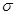 =57∙106 =57∙106
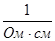 ); );  - глубина проникновения материала экрана, см; N – число витков; Dк – диаметр катушки, см - глубина проникновения материала экрана, см; N – число витков; Dк – диаметр катушки, см
Тогда,
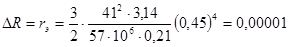 Ом. Ом.
Определим относительное изменение активного сопротивления, оно составит:
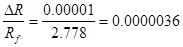 , т. е. сопротивление возрастет на 0,00036%. , т. е. сопротивление возрастет на 0,00036%.
Расчет сопротивления потерь, вносимого сердечником
Определим сопротивление потерь вносимое сердечником по формуле:
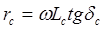 , (3,31) , (3,31)
где 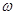 - круговая частота; Lc
– индуктивность сердечника; - круговая частота; Lc
– индуктивность сердечника; 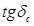 - тангенс угла потерь сердечника - тангенс угла потерь сердечника
Индуктивность сердечника рассчитаем по формуле:
Lc
=μс
L (3.32)
где μс
–магнитная проницаемость сердечника;
L-фактическая индуктивность;
Тогда,
Lc
=1,1∙21=23,1мкГ
Найдем численное значение 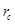
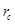 = 2∙3,14∙5∙23,1∙2,4∙10-4
=0,174Ом = 2∙3,14∙5∙23,1∙2,4∙10-4
=0,174Ом
Определим суммарное сопротивление потерь в катушке
 – суммарное сопротивление потерь, определяется как: – суммарное сопротивление потерь, определяется как:
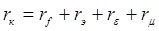 , (3.33) , (3.33)
где 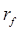 – сопротивление провода току высокой частоты, характеризующие эффект близости и поверхностный эффект; – сопротивление провода току высокой частоты, характеризующие эффект близости и поверхностный эффект; 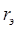 – сопротивление, обусловленное влиянием экрана; – сопротивление, обусловленное влиянием экрана; 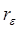 – сопротивление потерь в диэлектрике каркаса; – сопротивление потерь в диэлектрике каркаса; 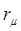 – сопротивление, обусловленное потерями в сердечнике; – сопротивление, обусловленное потерями в сердечнике;
Тогда,
 =1,99+0,0109+0,174+0,00001=2,17Ом =1,99+0,0109+0,174+0,00001=2,17Ом
Расчет добротности катушки
По найденным сопротивлениям потерь определим добротность катушки индуктивности по формуле:
Q=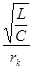 (3.34) (3.34)
Q=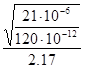 =193 =193
3.5 Определение температурного коэффициента индуктивности
Температурный коэффициент индуктивности (впредь ТКИ) является интегральной величиной, величиной состоящей из нескольких слагаемых, и определяется по формуле (3.35)
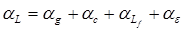 , (3.35) , (3.35)
где g
– геометрическая составляющая, 1/град;
aс
– составляющая, вносимая сердечником, 1/град; (с
=0.01∙10-6
1/град (по ист. 3))
ae
– составляющая, вносимая диэлектриком каркаса, 1/ град; (ae
=0,8∙10-6
1/ град (по ист. 3))
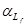 – высокочастотная составляющая, учитывающая влияние эффекта близости, 1/град. – высокочастотная составляющая, учитывающая влияние эффекта близости, 1/град.
Воздействие температуры приводит к изменению удельного сопротивления обмотки, так для меди 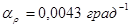 . Следствием этого является изменение глубины проникновения высокочастотных, составляющих переменного тока, что эквивалентно изменению диаметра витка обмотки. Подобная нестабильность является, высокочастотной составляющей ТКИ, которую можно определить через добротность катушки . Следствием этого является изменение глубины проникновения высокочастотных, составляющих переменного тока, что эквивалентно изменению диаметра витка обмотки. Подобная нестабильность является, высокочастотной составляющей ТКИ, которую можно определить через добротность катушки
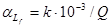 , (3.36) , (3.36)
где 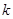 – коэффициент, зависящий от типа провода, – коэффициент, зависящий от типа провода, 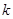 = 2 для катушек с круглым--проводом; Q – добротность катушки индуктивности. = 2 для катушек с круглым--проводом; Q – добротность катушки индуктивности.
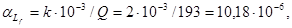
Геометрическая составляющая рассчитывается по формуле
 , (3.37) , (3.37)
где aD
– температурный коэффициент линейного расширения (ТКЛР) диаметра провода, 1/град; al
– ТКЛР длинны, 1/град; К – коэффициент, равный 0,37…0,45; D – диаметр каркаса, см;  – длина намотки, см. – длина намотки, см.
Так как составляющие aD
и al
идентичны (для меди они составляют по 1.7×10 -5
), то
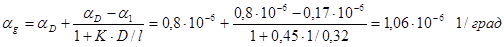
Тогда 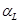 =1,06∙10-6
+0,8∙10-6
+10,18∙10-6
+0,01∙10-6
=12,022∙10-6 =1,06∙10-6
+0,8∙10-6
+10,18∙10-6
+0,01∙10-6
=12,022∙10-6
Данный ТКИ характеризует изменение фактической величины индуктивности в зависимости от изменения температуры окружающей среды, которое можно проанализировать пользуясь формулой (3.38)
 , (3.38) , (3.38)
Для заданных условий эксплуатации – В 3.1 по ГОСТ 15150-69, что соответствует общеклиматической группе, за Т2
– выбирается максимальная температура, а за Т1
– минимальная температура. Значения Т2
и Т1
взяты из ГОСТ 15150-69, Т2
= +45°С, Т1
= - 10°С. Пользуясь полученными значениями вычислим по формуле (3.35) возможное изменение фактической индуктивности катушки:
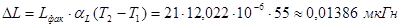 , ,
что составляет 0,069 % от фактической величины индуктивности.
4. ОПИСАНИЕ КОНСТРУКЦИИ
Катушка индуктивности состоит из провода марки ПЭВ-2 (d=0.05) ГОСТ 16186 – 74, намотанного на каркас из полистирола, обладающего низким тангенсом угла диэлектрических потерь и не высокой диэлектрической проницаемостью, что увеличивает добротность катушки. На каркас осуществляется однослойная намотка проводом, длиной 3,2 мм. Катушка с сердечником из карбонильного железа (цилиндрической формы с метрической резьбой) марки Р-100. Для придания конструкции, большей механической прочности, выводы пропаиваются припоем. Сборочный чертеж конструкции представлен в приложении.
ВЫВОДЫ
В ходе конструкторского расчета и анализа была определена конструкция катушки индуктивности. Расчет показал, что фактическая величина индуктивности отличается от требуемой на 0,285% при этом катушка индуктивности обладает высокой добротностью, что составляет 191(для такого вида катушек Q=(150÷400)) и низким ТКИ(αL
≤ 10÷50∙10-6
1/град, в нашем случае αL
=12.02∙10-6
1/град). Расчет оптимального диаметра провода показал, что можно использовать провод выбранного диаметра. Конструкция катушки индуктивности является не очень сложной, что желательно при годовой программе выпуска 1000 штук, которая вполне может являться серийным производством. Спроектированная катушка индуктивности, вполне удовлетворяет требованиям, поставленным в техническом задании.
СПИСОК ЛИТЕРАТУРЫ
1 Волгов В.А. Детали и узлы РЭА. – М.: Энергия. 1977. –656 с.
2 Устройства функциональной радиоэлектроники и электрорадиоэлементы: Конспект лекций. Часть I / М.Н. Мальков, В.Н. Свитенко. – Харьков: ХИРЭ. 1992. – 140 с.
3 Справочник конструктора РЭА: Общие принципы конструирования/ Под редакцией Р.Г. Варламова. – М.: Сов. Радио. 1980. – 480 с.
4 Фрумкин Г.Д. Расчет и конструирование радиоаппаратуры. – М.: Высшая школа. 1986. – 339 с.
|