Академия России
Кафедра Физики
Реферат на тему:
«Основные положения теории переходных процессов в электрических цепях»
Орел 2009
Содержание
Условия возникновения переходных колебаний в электрических цепях
Законы коммутации и начальные условия
Сущность классического метода анализа переходных колебаний в электрических цепях
Литература
Условия возникновения переходных колебаний в электрических цепях
На практике часто возникает необходимость анализа электрической цепи при переходе от одного стационарного состояния к другому.
Если цепь содержит только элементы активного сопротивления, то такой переход происходит мгновенно, так как эти элементы на запасают энергии.
При наличии в цепи реактивных элементов L и С для перехода от одного состояния к другому требуется некоторое конечное время. Это объясняется тем, что реактивные элементы могут запасать энергию, а затем отдавать ее.
Процесс перехода электрической цепи от одного установившегося состояния к другому установившемуся состоянию называется переходным (нестационарным) процессом.
Колебания, существующие при этом в цепи, называют переходными (нестационарными).
Частным случаем переходных колебаний являются свободные колебания. Они существуют в электрической цепи после прекращения внешнего воздействия за счет энергии, запасенной в реактивных элементах.
Таким образом, условиями возникновения переходных колебаний в электрической цепи являются:
– наличие в цепи реактивных элементов;
– наличие коммутации.
При этом под коммутацией понимают любые действия в цепи, приводящие к возникновению переходных процессов.
Приведем примеры коммутаций:
а) механическое соединение или разъединение на отдельных участках цепи. В теории считают, что такое действие осуществляется с помощью идеального ключа. На рисунке 1, а показан случай, когда идеальный ключ замыкается, а на рисунке 1, б – когда размыкается;
а) б)
Рис. 1
б) включение или выключение ЭДС или задающего тока источников.
а) Включение б) Выключение
Рис. 2
На рисунке 2, а показано схемное обозначение включения постоянной ЭДС и постоянного тока, а на рисунке 2, б их выключение.
Такое воздействие принято называть ступенчатым (перепадом, или скачком напряжения или тока). В случае 2,б иногда говорят, что "гасится" источник постоянной ЭДС или источник постоянного тока. При этом сам источник (его внутреннее сопротивление) механически из схемы не исключается. Отметим, что ступенчатое воздействие является простейшей функцией. Нахождение реакции на такое воздействие является одной из важных задач в теории переходных процессов (аналогично задаче нахождения реакции цепи на гармоническое воздействие в стационарном режиме).
в) другие воздействия, например, в виде импульсов различной формы, включение и выключение источников гармонических колебаний и др.
Переходные процессы играют важную роль в технике связи.
Они используются для получения напряжения или тока специальной формы (остроконечные импульсы, пилообразное напряжение и т. п.).
С другой стороны, за счет переходных процессов могут возникать искажения формы сигналов, что является нежелательным. Анализ переходных процессов позволяет оценить эти искажения, а также другие характеристики, составляющие основу методов синтеза устройств, предназначенных для оптимальной обработки сигналов.
В технике связи переходные процессы учитывают при расчете усилителей дискретных сигналов, фазосдвигающих цепочек, линий задержки и других устройств.
При анализе переходных процессов необходимо применять особые правила – законы коммутации и начальные условия.
Законы коммутации и начальные условия
Будем считать, что коммутация происходит в момент  , а все переходные процессы в цепи начинаются с момента  , т. е. непосредственно после коммутации. Состояние цепи до коммутации оценивается в момент  .
Законы коммутации относятся к энергоемким (реактивным) элементам, т. е. к емкости и индуктивности. Они гласят: напряжение на емкости и ток в индуктивности при конечных по величине воздействиях являются непрерывными функциями времени, т. е. не могут изменяться скачком.
Математически эта формулировка может быть записана следующим образом
 для емкости;
 для индуктивности.
Законы коммутации являются следствием определений элементов емкости и индуктивности.
Так для емкости
 ,
а для индуктивности
 .
Полученные интегралы с переменными верхними пределами являются непрерывными функциями их пределов (времени  ) при ограниченных значениях  и  , которые являются именно таковыми.
Физически закон коммутации для индуктивности объясняется противодействием ЭДС самоиндукции изменению тока, а закон коммутации для емкости – противодействием напряженности электрического поля конденсатора изменению внешнего напряжения.
При количественном анализе переходных колебаний в условия каждой конкретной задачи должны входить значения напряжений на емкостях и токов в индуктивностях цепи в момент коммутации, т. е. в начальный момент. Эти значения образуют начальные условия задачи. Ими, в силу законов коммутации, задаются те напряжения и токи в цепи, которые сохраняют свои значения в момент времени непосредственно после коммутации. Если в момент коммутации напряжение на всех емкостях цепи и токи во всех индуктивностях цепи равны нулю, то соответствующие начальные условия называются нулевыми.
Если же это не выполняется хотя бы в одном реактивном элементе цепи, то задача решается при ненулевых начальных условиях.
На практике при решении задач важное значение имеет умение находить начальные и конечные значения реакций.
Безошибочно это сделать можно только при твердом знании законов коммутации и их правильном применении. Проиллюстрируем это на примере.
Пусть в цепи, изображенной на схеме (рис. 3) и находящейся при нулевых начальных условиях в момент включается источник постоянного напряжения путем замыкания ключа. Требуется определить начальные (для ) и конечные (для  ) значения реакций.
Рис. 3
Решение.
Изобразим схему для (рис. 4) с учетом законов коммутации  (КЗ);  обрыв (ХХ),
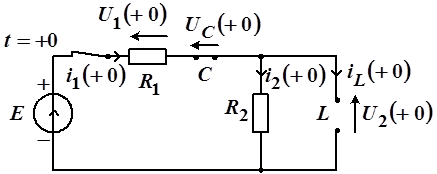
Рис. 4
откуда
 ;  ;  ;  .
Теперь определим реакции для с учетом того, что режим установился. Емкость при этом уже зарядится, и будет представлять собой обрыв. Следовательно, все реакции будут равны нулю, за исключением напряжения на емкости, которое будет равно  .
При анализе переходных колебаний в электрических цепях применяются следующие методы для нахождения реакций:
– классический, основанный на составлении и решении дифференциальных уравнений;
– операторный, основанный на применении преобразования Лапласа;
– временной, использующий переходные и импульсные характеристики;
– частотный, базирующийся на спектральном представлении воздействия (преобразование Фурье).
Укажем, что последних три метода применимы только для линейных электрических цепей, поскольку в их основе лежит метод наложения (суперпозиции).
Сущность классического метода анализа переходных колебаний в электрических цепях
Переходные процессы в электрических цепях описываются уравнениями, составленными на основании законов Кирхгофа для мгновенных значений напряжений и токов. Эти уравнения для различных цепей после соответствующих преобразований могут быть приведены к какому-либо из следующих видов:
1)  ;
2)  ;
3)  .
Первое уравнение – линейное, с постоянными коэффициентами  характеризует линейную цепь.
Второе, в котором, по крайней мере, один из коэффициентов (в данном случае  ) является функцией времени, описывает линейную цепь с переменными параметрами (т. е. параметрические цепи).
Третье, в котором хотя бы один из коэффициентов (в данном случае  ) является функцией  , описывает нелинейную цепь и является, в отличие от первых двух, нелинейным дифференциальным уравнением.
Рассмотрим пример.
Пусть на последовательный контур (рис. 5), находящийся при нулевых начальных условиях в момент посредством замыкания ключа начинает действовать источник напряжения величиной  . Требуется определить реакции.
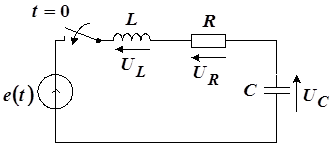
Рис. 5
Составим уравнение по второму закону Кирхгофа:
или
 . (1)
Пусть все элементы цепи линейны. Тогда уравнение (1) преобразуется к виду:
или
 ,
где:  ;
 ;
 ;  .
Получено линейное, в общем случае неоднородное дифференциальное уравнение второго порядка, которое решается относительно известными из математики методами.
Аналогичное уравнение получается и для параметрической цепи. Пусть теперь цепь является нелинейной, например, допустим, что индуктивность является функцией тока, т.е.  .
Тогда
и уравнение (1) будет иметь вид
 .
Оно может быть преобразовано в нелинейное уравнение второго порядка. Решение нелинейных дифференциальных уравнений, даже первого порядка, является весьма сложной, а иногда и неразрешимой задачей.
Литература
1. Белецкий А. Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986
|
