МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ.
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА М.Ф. РЕШЕТНЕВА.
Кафедра физики.
Реферат
по дисциплине "Физика"
На тему:
«Основы физики атмосферы. Термодинамические процессы в сухом и влажном воздухе. Термодинамические процессы фазовых переходов. Уравнение Клаузиуса-Клапейрона. Уравнение переноса водяного пара в атмосфере. Физические процессы образования облаков Динамические процессы а атмосфере»
Выполнил: студент 2-го курса
группы ИУТ-61
Нечаев А. С.
Проверил:
Баринов Г. И.
Красноярск 2007
Основы физики атмосферы
Уравнение состояния
Основным действующим на атмосферу внешним фактором является Солнце. Под воздействием солнечного излучения происходят разнообразные процессы переноса энергии, тепла и вещества между разными областями атмосферы и другими геосферами. Атмосфера, в основном, заполнена воздухом и примерный молекулярный вес воздуха, как хорошо известно, равен 29, что несколько больше молекулярного веса основной компоненты воздуха — азота N2, равного 28. Небольшое превышение молекулярного веса воздуха над молекулярным весом азота связано с тем, что следующая по объему компонента — кислород О2 имеет больший молекулярный вес — 32.
Уравнение состояния воздуха с большой точностью описывается уравнением состояния идеального газа:

где объем V
,
масса воздуха m, молекулярная масса µ
измеряются в обычных единицах системы СИ, R
— универсальная газовая постоянная. Давление Р
традиционно измеряется в барах, причем, бар выражается следующим образом через стандартные единицы Н (ньютон) и Па (единица давления паскаль равна силе в ньютонах, деленной на площадь в м2
):

Часто используется единица давления атм (атмосфера), равная 1 кг/см2
и близкая к одному бару.
Здесь целесообразно напомнить некоторые полезные для дальнейшего цифры. Часто выделяют так называемые «нормальные условия»:

Они представляют собой некоторые типичные, «нормальные» значения атмосферного давления и температуры 0°С, т.е. примерно 273 К. При этом объем одного моля идеального газа составляет 2,24 • 10-2
м3
, или 22,4 литра.
Чаще в физике атмосферы используется другая форма записи уравнения состояния, содержащая плотность воздуха р.
Уравнение следует из (13.1), если поделить на объем правую часть. Нередко используется не универсальная газовая постоянная R, а газовая постоянная для воздуха Ra
,
нормированная на молекулярный вес воздуха µ:

где

Отсюда плотность воздуха при нормальных условиях равна

Одним из самых существенных факторов, определяющих поведение атмосферы, является водяной пар — известный всем газ Н2О с молекулярной массой 18. Он присутствует в сравнительно небольших количествах в атмосфере, но в отличие от других компонент воздуха с водяным паром при типичных атмосферных температурах происходят фазовые переходы с выделением и поглощением тепла, поэтому его роль весьма значительна. Уравнение состояния воздуха при учете водяного пара меняется.
Напишем отдельно уравнение состояния для сухого воздуха с парциальным давлением Ра
и уравнение состояния для водяного пара, где е обозначает так называемую упругость водяных паров, или парциальное давление водяного пара:

Здесь введена газовая постоянная для водяного пара Rw
=
= R
/
pw
.
Уравнение состояния для смеси сухого воздуха и водяного пара будет несколько отличаться от уравнения состояния для сухого воздуха. Суммарная плотность смеси р
равна плотности сухого воздуха ра
плюс плотность воды pw
:

Учитывая, что
получим выражение для плотности:
где плотности воздуха и водяного пара выражены через соответствующие уравнения состояния, при этом парциальное давление сухого воздуха заменено на разность давлений влажного воздуха (смеси) и пара, поскольку давление паров плюс давление сухого воздуха есть суммарное давление смеси. После тождественных преобразований получим формулу


Поскольку парциальное давление водяного пара, как правило, не превышает 30-50 мбар, оно мало по сравнению с давлением
воздуха (~ 1 бар). Учитывая малость отношения — <С 1, можно переписать уравнение состояние влажного воздуха в виде

Сравнивая (13.2) и (13.3), нетрудно видеть, что присутствие водяных паров дает лишь небольшую поправку к уравнению состояния, которую можно интерпретировать как сдвиг температуры. Иногда вводится так называемая виртуальная температура, т. е. для воздуха с водяным паром можно заменить уравнение состояния (13.3) соотношением вида (13.2) с другой — виртуальной температурой. Иными словами, это температура сухого воздуха, имеющего такое же давление как влажный воздух. Виртуальная температура будет несколько больше, потому что молекулярный вес пара меньше. Если происходит добавление пара с замещением молекул воздуха, то смесь становится легче и плотность падает. А для того чтобы сухой воздух имел такую же плотность, нужно поднять его температуру, тогда его плотность уменьшится. Как упоминалось выше, давление водяных паров невелико, поэтому в ряде задач без фазовых переходов влиянием водяного пара на уравнение состояния можно пренебречь.
Переход фазовый
(ф.п.)- термодинамический процесс перехода вещества из одной фазы в другую;
первого рода
- фазовый переход, при котором претерпевают скачки первые производные от химического потенциала (S
и V
);
второго рода
- фазовый переход, при котором первые производные от химического потенциала непрерывны, но претерпевают скачки его вторые производные (cP
,  , ,  T
); T
);
монотропный
- односторонний ф.п., при котором переход от высокотемпературной модификации к низкотемпературной невозможен, тогда как обратный процесс осуществляется и протекает тем быстрее, чем выше температура;
энантиотропный
- взаимные превращения двух кристаллических модификаций, которые могут самопроизвольно протекать как в прямом так и в обратном направлениях в зависимости от условий.
Правило фаз Гиббса
- в равновесной термодинамической системе
, на которую из внешних факторов оказывают влияние только 2 фактора - температура и давление
(соответствуют слагаемому "2" в ур-нии), число степеней свободы (C) равно числу независимых компонентов (K) минус число фаз (Ф) плюс два: С = К - Ф + 2. Если Ф = 0, система инвариантна, Ф = 1 - моновариантна, Ф = 2- бивариантна и т.д.
Уравнение Клапейрона-Клаузиуса
для фазовых превращений 
равновесие "кристалл"  жидкость": жидкость": 
равновесие "жидкость" пар": пар":  , ,
если насыщенный пар подчиняется ур-нию состояния идеального газа
, то
при испарении  ; ; , при возгонке , при возгонке  ; ; . .
В интегральном виде 
Термодинамические процессы в атмосфере
В
атмосфере происходят различные термодинамические процессы, в частности, изотермические, адиабатические и другие знакомые по курсу молекулярной физики процессы. В основном атмосфера неизотермична, например, в тропосфере температура меняется с высотой довольно сильно, примерно на 6,5 °С на км. Но в областях тропопаузы, стратопаузы, мезопаузы в некоторых диапазонах высот ее приближенно можно считать изотермичной.
Как известно, распределение давления и плотности в изотермической атмосфере определяется формулой Больцмана. Разность давлений в слоистой и статичной атмосфере обусловлена весом выделенного объема воздуха:

Ось z
направлена вверх. Если заменить р
выражением, полученным из уравнения состояния (13.2), то получим уравнение

откуда после интегрирования следует формула Больцмана

где  — так называемая высота однородной атмосферы. — так называемая высота однородной атмосферы.
В соответствии с формулой Больцмана давление с высотой меняется экспоненциально, причем Н
определяет масштаб спадания давления по высоте, т. е. на высоте Н
давление падает в е раз. Формула для плотности будет аналогичной, потому что при постоянной температуре плотность пропорциональна давлению. Высоту однородной атмосферы можно выразить и через массу т
одной молекулы:

Численная оценка дает величину около 8 км:

Заметим, что уже на высотах в несколько километров спадание давления и плотности воздуха значительно, например, на высоте 2,5 км плотность составляет 70% от плотности на уровне моря. Однако, как правило, в атмосфере происходят заметные изменения температуры с увеличением высоты, и приближение
изотермической атмосферы явно неприменимо. Более подходящим приближением при рассмотрении перемещения частиц воздуха является адиабатическое приближение. При таком анализе обычно выделяется малая частица, представляющая собой «физически бесконечно малый» объем, но достаточно большая, в том смысле, что она содержит много молекул. Иными словами, предполагается, что частица достаточно велика по сравнению с масштабами микроструктуры среды и достаточно мала по сравнению с внешними характерными масштабами задачи. Поскольку воздух — плохой проводник тепла и его теплопроводность низка, можно считать, что по мере перемещения этой частицы с потоком других частиц, с ветром, она слабо обменивается энергией с окружающей средой, т.е. можно использовать адиабатическое приближение. Такая простейшая модель, тем не менее, отражает основное физическое явление и объясняет многие процессы в атмосфере.
Рассмотрим адиабатический процесс в атмосфере. Первое начало термодинамики имеет вид

Здесь приращение тепла δ
Q
равно приращению внутренней энергии dU
=
CV
dT
плюс работа ЗА =
P
dV
.
Отметим, что в общем случае только приращение внутренней энергии dU
является полным дифференциалом. Для частицы, которая будет перемещаться, не меняя своей энергии, можно написать δ
Q
=
О, т.е. приток тепла равен нулю, взаимодействие с окружающей средой отсутствует или, по крайней мере, пренебрежимо мало за время этого перемещения. Если мы хотим получить зависимость Р(Т),
надо перейти от дифференциала dV
к дифференциалу dP
.
Это несложно сделать, используя уравнение состояния идеального газа. Дифференцируя логарифм соотношения (13.1), получим

После интегрирования получается связь
Это так называемое тождество Майера. Далее, используя тождество Майера, заменяем дифференциал dV
на dP
в (13.5) и получаем

уравнение адиабатического процесса:

Отсюда отношение температур равно отношению давлений в степени R
/
Cp
.
Универсальная газовая постоянная равна, как известно, разности теплоемкостей

Тогда, заменяя R
на разность Ср — С
v
, получим для адиабатического процесса формулу

в которой отношение температур есть отношение давлений в степени 1 — 1/y где y=
Ср/С
v
.
Воздух при нормальных условиях состоит в основном из молекул N2 и О2. У таких двухатомных молекул при типичных атмосферных температурах колебательные степени свободы не возбуждаются, поэтому они имеют 5 степеней свободы и молярную теплоемкость при постоянном объеме Су = 5/2
R
,
а молярную теплоемкость при постоянном давлении Ср
= 7/2 R, тогда y = 7/5.
При адиабатическом подъеме, естественно, будет происходить охлаждение частиц воздуха. Давление в частице меняется так же, как и давление внешней среды. Частица — это условный элемент объема, в котором достаточно много молекул, и по мере перемещения воздуха давление в частице все время равно давлению среды. Но по мере подъема будет происходить изменение температуры частицы, и этот градиент температуры, полученный в адиабатическом приближении, называют адиабатическим градиентом температуры. Уравнение адиабатического процесса (13.6) связывает, заменяя приращение давления через гидростатическое равенство (13.4), получим уравнение для температуры при таком адиабатическом подъеме:

Адиабатический градиент температуры по высоте отрицателен и представляет собой отношение ускорения свободного падения gк удельной теплоемкости воздуха при постоянном
давлении . .
Полученное численное значение градиента больше, чем в реальной атмосфере ( ≈ 6-6,5 К). Завышение величины температурного градиента связано с точностью адиабатического приближения, но, главное, здесь не учтено, что при конденсации водяного пара будет выделяться тепло и поднимающаяся частица будет охлаждаться слабее, т. е. рассмотренное здесь охлаждение сильнее, чем в реальной атмосфере.

Подставляя сюда гидростатическое соотношение для приращения давления (13.4), получим

и далее аналогично (13.7)

Рассмотренные выше процессы относятся к сухоадиабатическим процессам. Название сухоадиабатический процесс не означает, что воздух сухой, он может содержать и водяной пар, но его уравнение близко к уравнению состояния сухого воздуха, пока не происходит выделения скрытой теплоты конденсации. Во влажноадиабатическом процессе происходит выделение скрытой теплоты. С выделением такой теплоты ситуация существенно меняется. В первом начале термодинамики для влажноадиаба-тического процесса будет фигурировать скрытая теплота δ
Q
,
отнесенная к массе, которая пропорциональна произведению относительного содержания dq
(
q
— безразмерная величина) влаги в воздухе и удельной теплоты парообразования L
.
Поэтому выделение тепла (со знаком «минус», поскольку при dq
> 0 тепло уходит из системы) определяется соотношением.
Итак, dT/dz — равен сухоадиабатическому градиенту минус добавка, в которую входит изменение относительного содержания пара в воздухе. Производную dq/dz— удобно переписать через производную по температуре:

Отсюда для влажно-адиабатического градиента получаем формулу

Добавок к единице в знаменателе представляет собой положительную величину, поскольку относительная плотность q
с температурой растет. Получается, что влажноадиабатический градиент ys
равен сухоадиабатическому градиенту ya
, деленному на величину, большую 1, т.е. он меньше сухоадиабатического градиента:

В качестве иллюстрации адиабатических процессов рассмотрим адиабатический подъем и последующее опускание частиц воздуха, например, при обтекании возвышенностей и гор (рис. 13.1, а). На рис. 13.1, б
изображена диаграмма адиабатических процессов, иллюстрирующая изменение температуры

с высотой. При перемещение частицы вверх из точки О
(с температурой T
0
на высоте z
=
0) температура линейно спадает. Когда температура уменьшается до температуры конденсации Тс
, на высоте конденсации zc
образуется облако. Далее происходит выпадение осадков из этого облака и выделение скрытой теплоты конденсации, что уменьшает охлаждение воздуха. Поэтому у влажноадиабатического процесса (между точками С
и A)
наклон —— меньше, чем у сухоадиабатического.
После того как выпадут все осадки, воздух становится сухим, и далее происходит спуск в долину (между точками Л
и В).
Из диаграммы несложно понять, что если стартовать с температуры Tq, то завершается процесс с другой температурой Тв
, которая всегда больше T
0
.
Подобное выпадение осадков в горах и повышение температуры воздушного потока достаточно часто наблюдается в природе и хорошо иллюстрирует сухо- и влажноадиабатические процессы. Если осадки остаются на горе, то в долину спускается сухой и теплый воздух. Такой ветер называется фён.
Устойчивость атмосферы
Термодинамическую устойчивость атмосферы также можно рассмотреть в рамках адиабатического приближения. Устойчивость атмосферы зависит от вертикального профиля температуры. Предположим, что в неподвижном слое атмосферы температура линейно убывает с высотой ∆z, например, как это происходит в тропосфере. Градиент температуры данного слоя характеризуется параметром β:

Тогда разность температур частицы и окружающей среды будет равна:

Пусть малая частица воздуха поднимается адиабатически на высоту ∆z, при этом ее температура будет меняться в соответствии с адиабатическим градиентом уа
:

Учитывая, что давление в частице равно давлению окружающего воздуха, изменение плотности в соответствии с уравнением состояния (13.2) определяется разностью температур:

Отсюда знак вариации плотности определяется разностью адиабатического градиента и существующего в слое градиента температуры:

Поэтому при yа
< β
частица становится менее плотной, чем окружающий воздух (
∆р
< 0), и возникает выталкивающая сила плавучести (архимедова сила), направленная вверх. В этом случае атмосфера находится в неустойчивом состоянии,
поскольку любая сместившаяся вверх частица будет продолжать это движение. При yа
> β
частица становится более плотной, чем окружающий воздух (
∆р
> 0), и направленная вниз архимедова сила возвращает частицу обратно в исходное положение. Это случай устойчивого равновесия атмосферы. Особо устойчивые состояния атмосферы наблюдаются в так называемых слоях инверсии, когда β
< 0 и температура возрастает с высотой. Температурные инверсии гасят вертикальные движения и конвекционные потоки, подавляют перемешивание воздуха. Такие инверсионные слои могут существовать достаточно длительное время и оказывать негативное влияние на состояние и экологию атмосферы, особенно в городах, поскольку приводят к накоплению загрязнений.
Динамика и глобальная циркуляция
Первоначально проведем качественное рассмотрение движения воздушных масс. Из курса механики известно, что физические тела, находящиеся на вращающейся планете в неинерциальной системе координат, приобретают дополнительное поворотное, или кориолисово ускорение. Кориолисово ускорение ак
есть удвоенное векторное произведение угловой скорости вращения Земли И
на скорость тела v
в неинерциальной системе координат:

Уравнение относительного движения материальной точки в неинерциальной системе координат может быть записано формально подобно уравнению движения в инерциальной системе координат, но с введением соответствующих дополнительных сил инерции. Иными словами, в неинерциальной системе координат появляется некоторая эффективная сила инерции, действующая со знаком «минус» и равная произведению массы тела на дополнительное ускорение. В частности, для описания кориолисова ускорения вводится плотность кориолисовой силы

Следует отметить принципиальное отличие сил инерции от обычных сил взаимодействия тел, состоящее в том, что для них нельзя указать, действие каких конкретно тел на данное тело ими описывается. Однако, не вдаваясь в детали, отметим, что в Северном полушарии под действием кориолисовой силы всякий движущийся объект, независимо от направления движения, будет отклоняться при движении вправо. Соответственно в Южном полушарии объект будет отклоняться влево от направления движения. Кориолисово ускорение имеет и вертикальную составляющую, но при обычных в атмосфере скоростях движения, не
превышающих сотни метров в секунду, эта составляющая мала (< 10-3
) по сравнению с ускорением свободного падения д.
При движении по экватору остается только вертикальная составляющая, и тело не отклоняется в горизонтальной плоскости. В остальных случаях при движении в горизонтальных направлениях кориолисова сила имеет существенное значение, во многих случаях она является определяющей.
Типичное поле давления воздуха на Земле неоднородно, оно имеет максимумы, минимумы, седловые точки. Неоднородность поля давления в атмосфере — следствие неоднородности поверхности планеты, содержащей континенты, океаны, моря, которые прогреваются по-разному. Рассмотрим некоторое поле давления с минимумом и максимумом (рис. 14.1). Поле давления размечено системой изолиний. Давление нарастает по изолиниям слева

направо. Здесь приведена качественная картина, без указания числовых значений давления, только с обозначением областей низкого (Н) и высокого (В) давлений. Под действием градиентов давления воздушный поток втекает в область низкого давления, с поворотом направо (в Северном полушарии) каждой втекающей частицы. Из области высокого давления воздушный поток вытекает также с поворотом направо. Вследствие такого движения образуются вращающиеся вокруг областей экстремумов давления потоки. Области пониженного давления с вращением против часовой стрелки (в Северном полушарии) называются циклонами, области повышенного давления с вращением по часовой стрелке — антициклонами. Нетрудно понять, что между
минимумом и максимумом давления будет наблюдаться перпендикулярный градиенту давления поток. Такое движение воздушных масс называется геострофическим ветром. Иными словами, геострофический ветер — это квазиравномерное движение воздушных масс под действием кориолисовых сил по изобарам перпендикулярно градиенту давления. Геострофическое приближение подразумевает равновесие между кориолисовой силой и градиентом давления, что часто хорошо выполняется на практике. В ряде случаев нужно учитывать движение воздуха и вдоль градиента давления, но при этом остается и геострофическая составляющая воздушного потока. Крупномасштабные течения общей циркуляции в атмосфере являются в основном квазигеострофическими. Основные закономерности квазигеострофических движений в атмосфере были поняты давно, еще в середине XIX столетия было сформулировано (Бейс-Баллот) правило: если стоять спиной к ветру, то слева будет область низкого давления, а справа — высокого (в Северном полушарии, а в Южном — наоборот). На рис. 14.2 приведен пример космического снимка Земли в ИК диапазоне, на котором хорошо просматриваются
несколько циклонических спиралей с разными направлениями вращения в Северном и Южном полушариях.
Рассмотрим систему глобальной циркуляции атмосферы. Сильнее всего наша планета нагревается в районе экватора, здесь больше падает и поглощается солнечной энергии на единицу площади. Там же идет сильное испарение, образование облаков и туч, большое количество осадков, и теплый воздух поднимается вверх. Таким образом, образуется глобальная ячейка циркуляции (ячейка Хэдли (Гадлея)): теплый воздух поднимается от экватора и опускается где-то в области 30-х широт. Отсюда следует, что в районе 30-х широт находится область высокого давления — область субтропических циклонов. Соответственно ветры от 30-х широт дуют по направлению к экватору, где находится область низкого давления — экваториальная ложбина и внутритропические зоны конвергенции. В районе 60-х широт также образуется область низкого давления, и между 30-ми и 60-ми широтами формируется еще одна ячейка глобальной циркуляции (ячейка Ферреля). Наконец между 60-й широтой и полюсом формируется полярная ячейка глобальной циркуляции с областью высокого давления на полюсе (полярный антициклон).
Система глобальной циркуляции атмосферы хорошо объясняется в рамках геострофического приближения (см. рис. 9.1). Ветры, которые дуют из области 30-х широт к экватору, отклоняются вправо (в Северном полушарии) и приобретают преобладающее северо-восточное направление — это так называемые северо-восточные пассаты. В Южном полушарии пассаты имеют юго-восточное направление. В целом пассаты, дующие из областей высокого давления 30-х широт к экватору, имеют общее восточное направление. Ветры, которые дуют из области высокого давления 30-х широт к области низкого давления 60-х широт, имеют общее западное направление, это так называемый западный перенос. Полярные ветры имеют восточное направление.
Отметим некоторые дополнительные особенности системы глобальной циркуляции атмосферы. Как сказано выше, в Северном полушарии между 30 и 60° преобладают западные ветры, а в Южном полушарии эти ветры заметно сильнее. Это связано с тем, что в 40-х широтах мы имеем фактически единый океан, не прерываемый континентами, только с узкой полосой суши в Южной Америке. Здесь над океаном ветры испытывают заметно меньшее торможение, разгоняются и образуют область
знаменитых «ревущих сороковых» широт, весьма опасных для мореплавателей. Кстати, и циклоны в Южной Атлантике почти не зарождаются. Есть еще любопытные исторические названия. В пору покорения Нового Света (конец XV-XVI в.) район максимума давления Северного полушария — 30-е широты получили название «конских» широт, потому, что очень часто в районе этих широт корабли попадали в штиль. А длительное стояние в штиль сокращало запасы воды и приводило к тому, что лошадей приходилось выбрасывать за борт, и их в ту пору много плавало в этих широтах.
Рассмотренная выше схема глобальной циркуляции атмосферы предполагает усреднение по достаточно большим периодам времени. Конечно, ежечасные и ежедневные реальные карты ветров заметно отличаются от схемы глобальной циркуляции в силу многих других локальных и региональных факторов.
Уравнения движения. Локальные эффекты
Рассмотрим далее основные закономерности динамики атмосферы на основе уравнения движения для частицы воздуха. Как обычно, выбираем достаточно малую частицу по сравнению с внешними масштабами задачи, но достаточно большую по сравнению с размерами молекул, чтобы ее можно было считать частицей сплошной среды. В названных пределах выбор объема при разбиении сплошной среды на частицы не должен играть роли, поэтому уравнение движения целесообразно нормировать на объем элементарной частицы и перейти к распределениям объемной плотности сил и плотности ускорения среды. Тогда уравнение движения будет иметь вид

Здесь слева плотность частицы р, умноженная на ее ускорение. Справа — несколько слагаемых, характеризующих объемную плотность массовых сил: объемные плотности сил тяжести р
g
,
кориолисовых сил — 2р
[ΩxV], сил трения p∆Vи градиент давления VP. Плотность сил трения определяется лапласианом скорости и коэффициентом µ∆V, характеризующим вязкость воздуха. Уравнение (14.1), называемое уравнением Навье-Стокса, описывает течение вязкой сжимаемой жидкости или газа. В целом, для описания движения сплошной среды кроме уравнения (14.1), характеризующего изменение плотности импульса вязкой жидкости, требуется уравнение непрерывности, а также уравнение
 |
состояния сплошной среды и уравнения изменения энергии и энтропии вязкой жидкости. Строго говоря, уравнение Навье-Стокса, описывающее движение сплошной среды, — это уравнение в частных производных, и полную производную по времени следует выражать через соответствующие частные производные, что приводит к нелинейности уравнения по скорости. Иногда удобно пронормировать уравнение Навье-Стокса на плотность и переписать в следующей форме, где фигурируют соответствующие ускорения и кинематический коэффициент вязкости  : :

Решение полной системы названных уравнений движения сплошной среды представляет собой весьма сложную задачу. Для иллюстрации мы рассмотрим лишь два частных случая решения уравнения Навье-Стокса применительно к динамике атмосферы.
Вначале рассмотрим вертикальные составляющие уравнения Навье-Стокса. Основными слагаемыми в правой части (14.1) являются объемная плотность силы тяжести и соответствующая вертикальная компонента градиента давления. Вертикальной составляющей кориолисового ускорения в (14.2) при обычных скоростях движения до сотни метров в секунду можно пренебречь (< 10-3
) по сравнению с д.
Если предположить малость вертикальных ускорений и пренебречь силами трения, получим уравнение гидростатики:

Добавляя сюда уравнение состояния идеального газа и предположение об изотермичности, получим барометрическую формулу, как это уже было проделано в предыдущем разделе.
Теперь рассмотрим уравнения (14.1), (14.2) в некоторой горизонтальной плоскости. Если движения считать очень медленными, пренебречь ускорением и силой трения, то останутся следующие слагаемые: горизонтальный градиент давления и кориолисова сила. Отсюда получается уравнение геострофического ветра:

из которого видно, что скорость не направлена по градиенту давления. Она направлена перпендикулярно к градиенту давления, поскольку они связаны через векторное произведение. Отметим,
что крупномасштабные процессы в атмосфере квазидвумерны и квазигеострофичны.
Подобные крупномасштабные движения воздушных масс хорошо видны на космических снимках. В область циклона с пониженным давлением стягиваются воздушные массы, поэтому спиралевидные облачные структуры с закручиванием против часовой стрелки являются естественными трассерами циклонов. Из области антициклона с повышенным давлением наблюдается также движение воздушных масс, но с вращением уже по часовой стрелке. Кстати, типичная энергия циклонов (не тропических) — это 1017
Дж. Для сравнения энергия мегатонной атомной бомбы 4 • 1015
Дж, т. е. циклон эквивалентен десяткам и сотням мегатонных бомб. Однако эта энергия распределена по большому пространству и вызывает лишь сравнительно медленное движение воздушных масс.
В особую группу выделяют сильные тропические циклоны, энергия которых достигает 1019
Дж. Мощные тропические циклоны традиционно именуют ураганами (английское название — hurricane) в Атлантике и тайфунами на Тихом океане. Скорость ветра в ураганах и тайфунах достигает 20-40 м/с и более, что приводит к существенным разрушениям, наводнениям, цунами и другим стихийным бедствиям. Нашествиям тропических циклонов подвержены в основном Атлантическое побережье США, Карибский регион, Юго-Восточная Азия, Индонезия, Австралия. Достаточно редко тайфуны заходят к нам, на дальневосточное побережье России. Поскольку мощные тропические циклоны представляют большую опасность, существуют различные службы наблюдения за ними, которые классифицируют их (ураганам и тайфунам присваиваются имена), определяют и прогнозируют траектории их движения. Космический снимок тропического циклона приведен на рис. 14.3.
Наряду с глобальной циркуляцией атмосферы существуют движения воздуха, связанные с локальными пространственными и временными факторами. Природа локальных ветров также имеет простое физическое объяснение. Первый пример таких локальных ветров и перемещений воздушных масс — это так называемые морской и береговой бризы.
Когда наступает день и ярко светит солнце, суша практически сразу прогревается, значительно быстрее воды. Причина в том, что теплоемкость воды гораздо больше, чем теплоемкость существующих грунтов, кроме того, вода прогревается на значительную глубину, поэтому
представляет собой более емкий резервуар тепла, чем практически не пропускающий оптическое и ИК излучение грунт. Воздух над сушей также прогревается быстрее. Далее прогревающийся воздух расширяется, плотность его понижается и нагретый воздух поднимается вверх. В результате над сушей образуется область низкого давления, в отличие от области более высокого давления над морем. Естественно, из области высокого давления в область низкого давления подтягивается прохладный воздух с моря — морской бриз. Циркуляция замыкается, и получается некоторый локальный круговорот вокруг берега. Здесь предполагается, что берег не содержит высоких гор, следовательно отсутствует заметный адиабатический подъем или опускание воздуха. Ночью имеет место противоположная ситуация. Суша быстро остывает, а вода отдает тепло значительно медленнее, поэтому ночью наоборот дует береговой бриз с суши на море. Такого рода ветры имеют естественную суточную периодичность.
Примером ветров, связанных с сезонной периодичностью нагрева, являются муссоны. Сравнительно устойчивая муссонная циркуляция наблюдается в Экваториальной Африке, на восточной и южной периферии Азии. Достаточно сильно это явление проявляется на полуострове Индостан. Летом хорошо прогревается сам полуостров и воздушные массы над ним, образуется область низкого давления, и ветер дует с моря. Естественно, это очень влажный ветер, который вызывает сезон дождей. В зимние месяцы суша охлаждается быстрее окружающего океана. Поскольку океан и воздушные массы над ним теплее, здесь образуется область низкого давления, и зимой сухие ветры дуют с континента на море. Отметим, что такое поведение давления над материками типично для внетропических широт: летом давление понижено, а зимой повышено.
Рассмотрим так называемые горно-долинные ветры. Здесь ситуация отличается от предыдущих примеров тем, что происходят неадиабатические процессы. Выше был рассмотрен фён, когда воздушные массы адиабатически поднимаются в гору, охлаждаются и с осадками теряют запас влаги, а при спуске с горы происходит адиабатический нагрев воздуха. В случае достаточно больших вершин и протяженных склонов гор происходит длительный подъем воздуха, который может прогреваться на склоне. Такой подъем с внешним нагревом будет, конечно, неадиабатическим. Тогда при прогреве воздуха на склоне долинный ветер, дующий из долины на гору, становится теплым. И наоборот, горный ветер достаточно долго втекает по склону гор в долину, и существуют условия для его радиационного охлаждения (ясное небо), — он теряет энергию на ИК излучение и заметно охлаждается.
Подобные холодные ветры с гор имеют различные местные названия. Такое явление наблюдается на Черноморском побережье в Крыму и в районе Новороссийска и называется бора. Подобный ветер на средиземноморском побережье имеет название мистраль.
В целом динамика атмосферы определяется как процессами глобальной циркуляции, так и локальными явлениями типа рассмотренных выше бризов, муссонов, горно-долинных ветров и т. д.
Погода и климат
Термины «погода» и «климат» весьма часто употребляются и хорошо всем известны. Под погодой понимается физическое состояние атмосферы у поверхности Земли в данный момент времени. Физическое состояние атмосферы характеризуется метеорологическими величинами (температура, давление, влажность, ветер, облачность, осадки) и атмосферными явлениями (гроза, туман, пыльная буря, метель и т.п.). Понятие климата связано с режимом температуры и осадков (совокупности атмосферных условий) на данной территории за длительный период времени. Можно сказать, что климат — это «синтез погод». Однако нет общепринятого определения масштаба времени, разделяющего синоптические процессы, формирующие погоду, и процессы формирования климата, поэтому при обсуждении проблем изменений климата следует уточнять о каком масштабе времени (и каких атмосферных условиях) идет речь. Проблемы различий и изменений климата привлекали к себе внимание с незапамятных времен. Еще древним грекам было понятно, что климат в
основном определяется средней высотой Солнца (широтой местности), наклоном солнечных лучей. Само слово «климат» имеет греческое происхождение и означает «наклон».
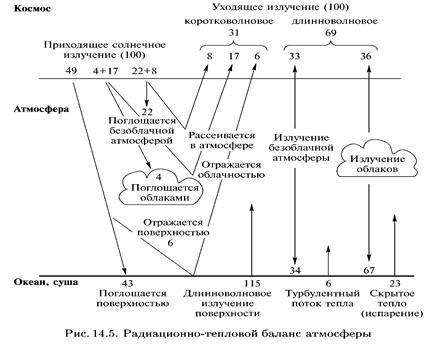
Процессы, определяющие погоду и климат, обусловлены как внутренними факторами и динамикой системы геосфер Земли, так и внешними факторами, прежде всего Солнцем. Прежде чем обсуждать проблемы погоды и климата, рассмотрим превращения солнечной энергии в атмосфере. На рис. 14.5 приведен усредненный радиационно-тепловой баланс в атмосфере, полученный по данным многочисленных измерений. Конечно, относительная величина всех составляющих баланса энергии сильно меняется в зависимости от времени, погодных условий и местности, однако анализ усредненных величин представляет существенный
интерес для физики атмосферы. Отметим, что цифры, определяющие баланс энергии и представленные на рис. 14.5, могут отличаться в различных источниках на 10-20%, что отражает несовершенство современных знаний об энергетическом режиме Земли.
На рис. 14.5 условно изображены два сорта излучения, одно — приходящее от Солнца, с максимумом по интенсивности в оптическом диапазоне, другое — уходящее от Земли. Уходящее излучение содержит как коротковолновое излучение, рассеянное и отраженное атмосферой и поверхностью Земли, так и длинноволновое, связанное с излучением самой планеты. Максимум этого длинноволнового излучения, как отмечалось в гл. 12, лежит в инфракрасной области спектра с длиной волны Лm
= 10 мкм. Если взять за 100% излучение, которое приходит от Солнца, то примерно 31% от него отражается и рассеивается атмосферой сразу: 17% облаками, 6% поверхностью земли и 8% безоблачной атмосферой. Назад уходит примерно 31%, а 69% этого коротковолнового излучения поглощается атмосферой (4% поглощается облаками, а 22% — безоблачной атмосферой) и 43% Землей. В установившемся стационарном Причем атмосфера излучает низкочастотное ИК излучение и вниз, в Землю (67 + 34 = 101%), а Земля излучает в атмосферу 115% ИК излучения + 29% энергии скрытым теплом и турбулентными потоками, что составляет 144% по энергии от падающего излучения. Хотя поток энергии от поверхности Земли превышает 100%, никакого противоречия с законом сохранения энергии здесь нет, поскольку Земля получает 43% по энергии высокочастотным излучением и 101% (67 + 34 = 101%) низкочастотным ИК излучением от атмосферы, что составляет те же 144%. Таким образом, между поверхностью Земли и атмосферой благодаря парниковому эффекту возникают встречные потоки энергии, которые дополнительно нагревают атмосферу и поверхность Земли.
Если приравнять излучаемую Землей энергию равновесному излучению некоторого эквивалентного черного тела, то получим аналогичную (12.3) оценку температуры с дополнительным множителем 1,441/4
= 1,1, т.е. температура этого тела будет составлять Т =
280 К. Согласно тем же экспериментальным данным атмосфера излучает в ИК диапазоне 170% (67% — безоблачная атмосфера и 103% — облака) энергии от первичного солнечного излучения. Если сопоставить излучаемую атмосферой энергию
равновесному излучению некоторого эквивалентного черного тела, то аналогично для оценки температуры получим соотношение вида (12.3) с дополнительным множителем 1,71/4
= 1,14, что соответствует Т =
290 К. Конечно, атмосфера и поверхность Земли заметно отражают падающее на них излучение, т. е. являются не абсолютно черными, а «серыми» телами, однако при сопоставлении с излучением некоторого эквивалентного черного тела это учитывается соответствующим коэффициентом серости. Полученные оценки довольно близки к реальным средним температурам атмосферы и поверхности Земли. Для более точного анализа необходим учет многих факторов, в частности, неравновесности излучения Земли и атмосферы, процессов переноса излучения, тепла, импульса и т. д.
Проблемы анализа динамики атмосферы и океана, предсказания погоды и климата представляют собой сложный комплекс физических и математических задач. Ранее прогнозы погоды основывались, как правило, на экстраполяции уже зарегистрированных данных. Метеорологи анализировали карты погоды, эволюцию областей высокого и низкого давления, движение и развитие фронтов, распространение облачности и другие подобные факторы и на этой основе давали прогноз. Искусство прогнозирования погоды состоит в учете многих факторов и возможности предвидения изменения состояния атмосферы. В истории метеорологии известно немало лиц, обладавших уникальными способностями в прогнозировании погоды. На основе накопленного опыта они могли определять, как будет в последующие дни меняться давление, положение фронтов и температура. Однако опыт выдающихся прогнозистов практически не передается последующим поколениям метеорологов.
В противоположность этому искусству метеорологов прошлого современная наука прогнозирования основывается на использовании математических моделей атмосферы и океана, поэтому используемые метеорологами современные методы называются численными методами прогноза погоды. Реализация подобных численных методов прогноза погоды стала возможной с 50-х годов XX в., когда появились соответствующие электронно-вычислительные машины. Прогноз состояния атмосферы в данном месте на срок до трех суток осуществляется путем интегрирования уравнений движения и переноса в атмосфере. В таком временном интервале атмосферные процессы можно считать адиабатическими, т.е. пренебрегать притоком энергии извне и диссипацией энергии за счет вязкости. По известному начальному состоянию
атмосферы рассчитываются временные и пространственные изменения. Поэтому для точного прогноза погоды необходима детальная и точная информация о начальном состоянии атмосферы. Требуемые исходные данные поставляет, главным образом, мировая сеть метеостанций и сеть станций радиозондирования атмосферы. Высотные радиозонды, запускаемые на воздушных шарах на высоты до 35 км измеряют температуру, давление, влажность воздуха и передают эту информацию по радио, кроме того, с Земли определяется и скорость ветра по положению радиозонда в пространстве. Станции радиозондирования расположены в основном в экономически развитых странах и отстоят друг от друга на расстояния порядка сотен километров. С начала 60-х годов регулярно запускаются метеорологические спутники, которые регистрируют распределения метеорологических параметров, осуществляют съемки распределений облаков, циклонических систем и т. п. Особо ценны спутниковые данные над океанами, где сеть метеорологических пунктов и станций радиозондирования весьма разрежена. В соответствии с разработанными Всемирной метеорологической организацией международным соглашением метеорологические данные со всего мира передаются в мировые центры данных в Москве, Вашингтоне и Мельбурне, а также во все национальные метеорологические учреждения.
Отметим, что ошибки, которые неизбежно вносятся в математическую модель, главным образом из-за неточности измерений, в процессе расчета имеют тенденцию к росту. Поэтому при расчете параметров состояния атмосферы на неделю или более ошибки, как правило, становятся столь большими, что исчезает возможность прогноза. Для предсказания на длительные сроки температуры, усредненной по времени и пространству, детерминированное описание не дает хороших результатов, и в этих случаях используются статистические методы прогноза, основанные на представлении о линейной регрессии. На возможность того, что малые возмущения начального состояния атмосферы могут привести со временем к существенным изменениям конечного состояния атмосферы и создать проблему предсказуемости, указывал А. Н. Колмогоров более 40 лет назад в следующей образной форме: «Представим себе две одинаковые планеты с совершенно идентичными состояниями атмосферы. Если на одной из них выйти на крыльцо и махнуть платком, а на другой этого не сделать, то через какое-то время погода на этих планетах станет совершенно различной».
В определенном смысле, еще более сложной проблемой является проблема анализа и предсказания климатических изменений. Если в случае предсказания погоды существует возможность постоянного сравнения «теории» (результатов численных расчетов) с «практикой» и последующей корректировки методов прогноза, то для предполагаемых климатических изменений на протяжении десятков, сотен и более лет такая возможность существенно ограничена. Земная климатическая система включает в себя все основные геосферы: атмосферу, гидросферу, литосферу, криосферу и биосферу. Следует отметить сложность структуры и взаимосвязей в земной климатической системе, ее неоднородность, нелинейность и нестационарность.
Облака атмосферные
, скопление в атмосфере продуктов конденсации
водяного пара
в виде огромного числа мельчайших капелек воды или кристалликов льда либо тех и других. Аналогичные скопления непосредственно у земной поверхности называется туманом
. облака — существенный погодообразующий фактор, определяющий формирование и режим осадков, влияющий на тепловой режим атмосферы и Земли и т.д. облака покрывают в среднем около половины небосвода Земли и содержат при этом во взвешенном состоянии до 109 т воды. Облака являются важным звеном влагооборота
на Земле, они могут перемещаться на тысячи км, перенося и тем самым перераспределяя огромные массы воды.
Образование облаков связано с возникновением в атмосфере областей с высокой относит. влажностью. Наличие в атмосфере огромного числа мельчайших частиц, играющих роль ядер конденсации
, обеспечивает появление зародышевых капель уже при достижении насыщения. Условия же насыщения создаются в результате охлаждения воздуха, вызванного, например, расширением его при упорядоченном подъеме на фронтах атмосферных
(так образуются облака Ns и системы Ns—As—Ac), при неупорядоченном турбулентном перемешивании или волновых движениях (St, Sc, Ac), при конвективном подъеме (Cu, Cu Cong, Cb), при отекании горных препятствий (Ac) и др. Дальнейшее охлаждение воздуха приводит к появлению избыточного пара, который поглощается растущими каплями. Т. о., первоначально капли растут преимущественно за счёт конденсации водяного паратмосфера Затем по мере их укрупнения, всё большую роль начинают играть процессы столкновения и слияния капель друг с другом (т. н. коагуляция облачных элементов
). Коагуляционный механизм — основной механизм роста облачных капель радиусом более 30 мкм. При отрицательных температурах облака могут быть капельные (переохлажденные), кристаллические или смешанные, т. е. состоящие из капель и кристаллов. Малые размеры облачных капель позволяют им долго сохраняться в жидком виде и при отрицательных температурах. Так, при —10 °С облака в половине случаев капельные, в 30% — смешанные и лишь в 20% кристаллические. Переохлажденные же капли в облака встречаются вплоть до —40 °С. Пересыщение над кристаллами значительно больше, чем над каплями (насыщающая упругость водяного пара над льдом ниже, чем над водой), благодаря чему в смешанных О. кристаллы растут значительно быстрее капель, что способствует выпадению осадков.
Многообразны и сложны физические процессы, управляющие развитием облаков Возникнув на ядрах конденсации, облачные капли растут, перемещаются внутри облака, выносятся за его пределы и испаряются. Время жизни облачных частиц может быть во много раз меньше времени жизни облака в целом. Цикл жизни облака в целом завершается его испарением. Выпадение осадков способствует уносу воды и ускоряет процесс разрушения облака. Длительное существование облака объясняется малыми скоростями падения частиц (капли радиусом 1—10 мкм падают со скоростью 0,05—1,2 см/сек), наличием восходящих движений воздуха, которые не только поддерживают облачные частицы, но и вместе с турбулентными движениями обеспечивают приток водяного пара и способствуют зарождению новых частиц.
Список использованной литературы
1. Трухин В. И., Показеев К. В., Куницын В. Е. Общая и экологическая геофизика.
— М.: ФИЗМАТЛИТ, 2005. — 576 с.
2. Мейсон Б. Дж. Физика облаков / Перевод с англ. – Л.: Гидрометеоиздат, 1961. – 541 с.
3. Качурин Л. Г. Физические основы воздействия на атмосферные процессы. – Л.: Гидрометеоиздат, 1989.
4. Роджерс Р.Р. Краткий курс физики облаков/Пер. с англ. – Л.: Гидрометеоиздат, 1979. – 231 с.
|