Министерство образования и науки Российской Федерации
Федеральное агентство по образованию ЮУрГУ
Кафедра” Прикладная механика, динамика и прочность машин”
Проектирование масляного выключателя
Челябинск 2007 год
Содержание
1. Задание на курсовое проектирование
2. Описание работы масляного выключателя
2.1 Фаза отключения
2.2 Фаза включения
3. Определение геометрических параметров привода
3.1 Проектирование шарнирного четырёхзвенника
3.2 Проектирование кинематической схемы выключателя с приводом
4. Кинематический анализ механизма
5. Динамический анализ механизма
5.1 Приведение масс механизма в фазе отключения
5.2 Определение параметров отключающей и буферной пружин
5.3 Построение фазовой траектории контактных стержней в фазе отключения
5.4 Определение времени отключения
5.5 Приведение масс механизма в фазе включения
5.6 Приведение сил статического сопротивления к штоку двигателя
5.7. Выбор силовой характеристики двигателя
5.8 Построение фазовой траектории контактных стержней в фазе включения
5.9 Определение времени включения
6. Силовой расчет механизма привода
7. Расчет деталей механизма на прочность
7.1 Расчет осей шарниров
7.2 Расчет рычага четырехзвенника
Заключение
Список литературы
Задание на курсовой проект
Спроектировать привод к масляному выключателю типа ВМГ-10, взяв за основу привод типа ПЭ-11. Определить время включения и время отключения выключателя со спроектированным приводом.
Исходные данные к проекту сведены в таблицу 1.1.
Таблица 1.1. Исходные данные
| Цифра варианта 1 |
Цифра варианта 5 |
Цифра варианта
9
|
| Ψ0 |
р |
Vp
, м/с |
Vmax
/Vp
|
H, мм |
hk
, мм |
Gk
, Н |
| 43 |
1.45 |
3.4 |
1.7 |
280 |
56 |
52 |
где
р – отношение длин шатуна АВ и кривошипа О1
А;
Vp
– скорость контактных стержней в момент размыкания;
Vmax
– максимально допустимая скорость контактных стержней;
Н – полный ход контактных стержней;
hk
– ход в контактах контактных стержней;
Gk
– вес одного контактного стержня.
2.
О
писание работы механизма
Схема выключателя ВМГ-10 и привода типа ПЭ-11:

Рисунок 2.1. Схема выключателя ВМГ-10 (позиции 1-6) с приводом типа ПЭ-11 (позиции 7-11): 1 – розеточный контакт (3 шт.); 2 – контактный стержень (3 шт.); 3 – коромысло выключателя (3 шт.); 4 – отключающая пружина; 5 – буферная пружина; 6 – демпфер; 7 – тяга; 8 – коромысло четырехзвенника; 9 – шатун; 10 – кривошип; 11 – щека запорного механизма; 12 – пружина запорного механизма; 13 – фиксатор; 14 – пружина фиксатора; 15 – опорная скоба; 16 – пружина опорной скобы; 17 – шток двигателя.
2.1 Фаза отключения
В положении «включено» (рис. 2.1) буферная пружина 5 сжата, а отключающая 4 – растянута. Они стремятся повернуть коромысло по часовой стрелке. Тяга 7 растянута, а шатун 9 и кривошип 10 сжаты. Щека 11 опирается на фиксатор 13.
При повороте фиксатора 13 против часовой стрелки вокруг оси О5
(вручную или с помощью электромагнита, который на схеме не показан) щека 11 освобождается и под действием силы со стороны кривошипа 10 поворачивается вокруг оси О4
, сжимая пружину 12. При этом шарнир А перемещается влево по торцу опорной скобы до тех пор, пока не срывается с него и падает вниз. Коромысло 8 и коромысло 3 поворачиваются по часовой стрелке, поднимая подвижные контакты 2. После размыкания контактов пружина 5 садится на свои упоры, а механизм движется под действием пружины 4. В конце поворота коромысла 3 включается в работу демпфер 6, который останавливает разогнавшийся механизм, поглощая его кинетическую энергию.
После срыва шарнира А с торца скобы щека 11 под действием пружины 12 возвращается в исходное положение. Фиксатор 13 под действием пружины 14 поворачивается по часовой стрелке и фиксирует щеку в исходном положении. Выключатель находиться в положении «отключено» и готов к включению.
2.2 Фаза включения
Включение производится перемещением вверх штока 17 (рис.2.1), приводимого в движение электромагнитным, пневматическим или гидравлическим двигателем. Поднимая вверх шарнир А, шток поворачивает кривошип 10 четырехзвенника О1
АВО2
вокруг временно неподвижной оси О1
. При этом коромысло 8 и коромысло 3 поворачиваются против часовой стрелки, опуская стержни 2 до полного входа их в розеточные контакты 1. Правое плечо коромысло 3 натягивает отключающую пружину 4 и сжимает буферную пружину 5.
Перемещаясь вверх, шарнир А отжимает вправо опорную скобу 15 под действием пружины 16 возвращается назад, запирая механизм в положении «включено». Шток 17 опускается вниз. Механизм готов к отключению.
Рассмотрев работу механизма, видим, что привод выключателя необходим только в фазе включения и его назначение состоит в преодолении сил отключающей и буферной пружин, сил трения и сил инерции. Поэтому рассчитать и спроектировать привод можно, не рассматривая фазу отключения, в которой движение всего механизма осуществляется за счет потенциальной энергии отключающей и буферной пружин.
3. Определение геометрических параметров привода
Целью данного раздела является определение геометрических параметров привода. При проектировании передаточных механизмов учитывают два основных фактора:
1. Проворачиваемость звеньев, т. е. возможность непрерывного перехода ведущего звена (кривошипа) из начального положения в конечное.
2. Углы давления, т. е. углы между направлением действия силы и вектором скорости соответствующей ведомой кинематической пары, за весь цикл работы механизма не должны превышать допускаемых значений. При увеличении этих углов в механизме возрастают нагрузки, увеличиваются потери энергии на трение (т. е. снижается КПД).
Механизм привода осуществляет преобразование прямолинейного движения штока двигателя во вращающее движение коромысла выключателя при включении, а также обеспечивает согласование силовых характеристик двигателя и потребления энергии. Для построения симметричного четырёхзвенника (рис. 3.1) рассчитаем необходимые параметры, зададим значения углов: 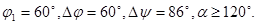 При выборе углов ψ0,φ0 учитывается: что при увеличении этих углов возрастают силы сопротивления движению в начале и конце фазы включения, а при уменьшении этих углов растут габариты передачи. При выборе углов ψ0,φ0 учитывается: что при увеличении этих углов возрастают силы сопротивления движению в начале и конце фазы включения, а при уменьшении этих углов растут габариты передачи.
Окончательное значение линейных размеров четырёхзвенника может быть установлено лишь после силового расчёта, когда из условий прочности будут найдены диаметры шарниров в точках А, В, О2 и оценка возможности конструктивного выполнения механизма в пределах найденных габаритов.
3.1 Проектирование шарнирного четырёхзвенника
Полный ход штока: hш=H/3 (3.1)
hш=280/3=93.33 (мм);
радиус кривошипа О1А: RA=hш/2*sin(φ0) (3.2)
Ra=93.33/2*sin(30)=93.33 (мм);
радиус кривошипа O2B: RB=RA*cos(φ0) (3.3)
RB=93.33*cos(30)=68,43 (мм);
длины апофем: аа=Ra*cos(φ0) (3.4)
aB=RB*cos(ψ0) (3.5)
aa=93.33*cos(30)=80.83 (мм);
aB=68.43*cos(43)=50 (мм);
длинашатуна: Lш=p*Ra (3.6)
Lш=1.45*93.33=135.28 (мм);
длина О1О2:  (3.7) (3.7)
где Lш –длина шатуна АВ;
аа, аВ- длины апофем;
l0= (мм); (мм);
Полученные размеры четырёхзвенника округляем по ГОСТу 66636-69 и строят в масштабе µL(рис 3.1).
Округлив по ГОСТу 66636 - 69 получим:
Ra=95 (мм), RB=67 (мм), Lш=140 (мм).
Масштаб µLопределяется из соотношения:
Ra=µL*О1А (3.8)
где О1А- длина, выбирается произвольно тогда получим
µL=Ra/O1A (3.9)
µL=95/47.5=0.002 (м/мм);
Длины звеньев АВ, О2В, О1О2, для построения четырёхзвенника определяются из выражении:
AB=Lш/µL (3.10)
AB=140/0.002=70 (мм);
О2В=RB/µL(3.11)
O2B=67/0.002=33.5 (мм).
3.2 Проектирование кинематической схемы выключателя с приводом
Для построения кинематической схемы всего механизма масляного выключателя, четырёхзвенник О1А1В1О2следует повернуть на (90+γ) градусов против часовой стрелки (рис 3.2), где
γ=arctg(r/Lш) (3.12)
где r- параметр, r=aa-aB=80-50=30 (мм),
γ=arctg(30/140)=12.5°.
Коромысло ВO2С будем проектировать т.о., чтобы в крайних положениях прямая O2С образовывала с горизонталью одинаковые углы ψ0=0.5*(ψ2-ψ1). Тогда зависимость между длиной второго плеча коромысла Rc и отношением длин плеч коромысла выключателя EO3M:
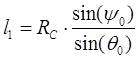 (3.13) (3.13)
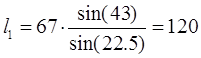 (мм); (мм);
где: l1- длина DО3
, мм;
L – длина ЕО3
мм;
Rc- плечо коромысла, Rc=RB=67 (мм);
Длина тяги CD практически не влияет на кинематику системы, поэтому зададим её такой, чтобы схему механизма удобно было располагать на чертеже. При определении параметров отключающей и буферной пружин считалось, что скорость контактов стержня практически совпадает с вертикальной проекцией скорости шарнира Е. Это условие выполняется достаточно точно во всех точках траектории движения шарнира при малом угле полного поворота коромысла 2θ0. Однако очень малый угол приводит к значительному увеличению размера L и соответственно габаритов выключателя. Исходя из этих соображений, зададим 2θ0=45°, тогда можем найти L:
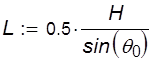 (3.14) (3.14)
L=0.5*280/sin(22.5°)=360 (мм).
Длину рычага l2 определяют из соотношения  =L/l2, где =L/l2, где
α- коэффициент относительной длины рычага коромысла;
α=0.4;
l2=0.4*360=150 (мм).
4. Кинематический анализ механизма
Основной задачей кинематики механизма является изучение движения его звеньев; при этом действующие на звенья силы не учитываются.
Определим отношение скоростей точек C,D, E, М, К коромысла выключателя кскорости штока двигателя в зависимости от положения штока.
Разделим дугу, описываемую точкой А кривошипа О1
А при переходе механизма из положения «отключено» в положение «включено» на шесть равных частей (рис. 4.1). Вычертим механизм в крайних и пяти промежуточных положениях, соответствующих семи положениям точки А. Дополнительное восьмое положение механизма получаем, когда подвижные контакты касаются неподвижных контактов(номер этого положения 6к). Для нахождения этого положения механизма, от нижнего (включённого) положения (точка Е2, рис. 4.1) откладываем перемещение подвижного контакта равное hk.
Для решения задачи скоростей, пронумеровываются звенья механизма, начиная с кривошипа О1А. Определяется вид их мгновенного движения.
Затем в каждом из положений механизма определяем линейные скорости точек A, B, C, D, E, М, а также угловые скорости звеньев. Линейную скорость ведущего звена (шток двигателя) будем задавать постоянной и равной единице, поскольку необходимые в дальнейшем передаточные функции представляют отношения соответствующих линейных скоростей к линейной скорости ведущего звена. Таким образом полученные скорости смаштабированными в Vш раз:
Ṽi=Vi/Vш, где i- соответствующая точка механизма. При этом вертикальная проекция скорости точки А, равная скорости штока двигателя. Считается также, что вертикальные проекции скоростей точек C и D одинаковы (VCY
=VDY
). Расчет скоростей ведется методом мгновенного центра скоростей (МЦС). Рассмотрим положение 1 (рис. 4.1).
ṼA1=Vш/cos(φ0-φi), (4.1)
где φ0=30°; φi- угол отсчитывается от положения «отключено» (φi меняется от 0° до 60°).
VA1=1/cos(30°-0°)=1.15.
Линейная скорость точки В для 1-го положения механизма определяется с помощью МЦС. Для звена АВ МЦС точка Рк лежит на пересечении перпендикуляров к скоростям точек А и В. Зная положение МЦС находим угловую скорость:
ω21=VA1/(A1PK1*µL), (4.2)
где А1Рк1- расстояние от точки А1 до Рк1 в мм;
µL-масштаб чертежа;
ω21=1.15/230*0.002=2.5.
Скорость точки В: VB1= ω21*B1PK1*µL, (4.3)
где B1PK1- расстояние от точки В1 до МЦС в мм;
VB1=2.5*272*0.002=1.36
Коромысло ВО2С совершает вращательное движение, определим его угловую скорость:
ω31=VB1/RB(4.4)
ω31=1.36/67=0.02.
Линейная скорость точки С:
VC1=ω31*Rc(4.5)
VC1=0.02*6.7=1.36.
При принятых допущениях (вертикальные проекции скоростей точек C и D одинаковы VCY
=VDY
), определяем линейную скорость точки D:
VD1=VC1*cos(ψ0-ψ1)/cos(θ0-θ1), (4.6)
Углы ψ1,θ1- отсчитываются от положения «отключено»;
VD1=1.36*cos(43°-0°)/cos(22.5°-0°)=1.08.
Коромысло выключателя ЕО3М совершает вращательное движение, его угловая скорость:
ωо3=VD1/l1, (4.7)
где l1-длина DO3 в мм;
ωо3= 1.08/120=0.009.
Линейные скорости точек Е и M:
VE1=VD1*L/l1, (4.8)
VM1=VD1*l2/l1, (4.9)
где l2 – длина рычага О3М в мм;
VE1=1.08*360/120=3.24,
VM1=1.08*150/120=1.35.
Скорость точки К определим, приняв, что вертикальная проекция скорости точки Е равна скорости подвижного контакта: VK1=VE1*cos(θ0-θ1) (4.10)
VK1=3.24*cos(22.5°- 0°)=2.99.
Координаты i- ых положений штока отсчитываемые от положения «отключено» вычисляются:
Sш1=Ra*[sin(φ0)-sin(φ0-φ1)] (4.11)
Sш1=95*[sin(30°)-sin(30°-0°)=0.
Координаты Ski положений подвижного контакта методом непосредственных измерений.
Результаты занесены в таблицу 4.1, и по ним построены графики VC(Sш), VD(Sш), VE(Sш), VK(Sш), VM(Sш), Sk(Sш) (рисунки 4.2, 4.3).
Таблица 4.1. Значение передаточных функций
| № пп |
ji
|
ψi |
θi |
Sшi,мм |
Ski
мм
|
Ṽ̃Ai
|
ṼBi
|
ṼCi
|
ṼDi
|
ṼEi
|
ṼKi
|
ṼMi
|
| 1 |
0 |
0 |
0 |
0 |
0 |
1.15 |
1.36 |
1.36 |
1.08 |
3.24 |
3.12 |
1.35 |
| 2 |
10 |
14.3 |
7.5 |
15 |
42 |
1.06 |
1.17 |
1.17 |
1.06 |
3.18 |
3.07 |
1.33 |
| 3 |
20 |
28.6 |
15 |
31 |
90 |
1.02 |
1.09 |
1.09 |
1.05 |
3.15 |
3.04 |
1.31 |
| 4 |
30 |
42.9 |
22.5 |
47.5 |
140 |
1 |
1 |
1 |
1 |
3 |
3 |
1.25 |
| 5 |
40 |
57.2 |
30 |
64 |
180 |
1.02 |
1.07 |
1.07 |
1.05 |
3.15 |
3.04 |
1.31 |
| 6k |
47.5 |
69 |
37 |
76 |
228 |
1.05 |
1.11 |
1.11 |
1.055 |
3.165 |
3.06 |
1.32 |
| 6 |
50 |
71.5 |
37.5 |
80 |
232 |
1.06 |
1.13 |
1.13 |
1.06 |
3.18 |
3.07 |
1.33 |
| 7 |
60 |
86 |
45 |
95 |
280 |
1.15 |
1.36 |
1.36 |
1.08 |
3.24 |
3.12 |
1.35 |
5. Динамический анализ механизма
Задача динамики - анализ загруженности реального механизма. Для упрощения её решения, механизм с одной степенью свободы с совокупностью всех звеньев и усилий заменяют эквивалентной с точки зрения загруженности привода динамической моделью.
Динамическая модель представляет собой одно звено – звено приведения, совершающая простое движение, с переменной массой mпр, с действующим на него усилием двигателя FДВ, приложенного со стороны привода и силами полезных и вредных сопротивлений FСТ.
Определение параметров mПР(Sш) – приведённой массы при поступательном движении звена приведения, называется приведением масс механизма. Основной этап построения динамической модели – приведение статических сил и статических моментов пар сил.
5.1 Приведение масс механизма в фазе отключения
В этом разделе строится приведенная динамическая схема механизма, рассмотрение движения которой позволяет выбрать параметры отключающей и буферной пружин. Этот этап работы называется приведением масс механизма [1].
Выражение для определения приведенной масс:
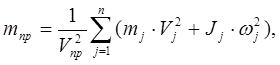 (5.1) где: (5.1) где:
Vпр
– скорость точки приведения, м/с;
mj
– масса j-ого звена механизма, кг;
Jj
– момент инерцииj-ого звена относительно центра тяжести, кг/м2
;
Vj
– скорость центра тяжести j-ого звена, м/с;
ωj
– угловая скорость j-ого звена, рад/с;
n – число Скорости Vj и ωj, входящие в формулу (5.1), должны быть выражены через скорость Vпр
, однако так как на стадии проектирования неизвестны массы mj
и моменты инерции Jj
большинства звеньев механизма, то непосредственно формулой (5.1) воспользоваться нельзя. В данном случае прибегнем к различным упрощениям. Одно из них – пренебрежение в сумме (5.1) большинством малых слагаемых.
В качестве точки приведения может быть использована любая точка механизма. В данном случае возьмем точку Е1
крепления подвижного контакта, т.к. скорость подвижных контактов является определяющей при выборе параметров привода. Поскольку в рассматриваемой конструкции основной вклад в mпр
вносят контактные стержни, с достаточной степенью точности можно принять
 (5.2) где (5.2) где
Gk
– вес одного контактного стержня, Н;
g – ускорение свободного падения, м/с2
.
5.2 Определение параметров отключающей и буферной пружин
Оптимальные характеристики механизма при отключении достигаются в том случае, если зависимость скорости контактных стержней от их перемещения V(S) (фазовая траектория) имеет вид, показанный на рисунке 5.1.
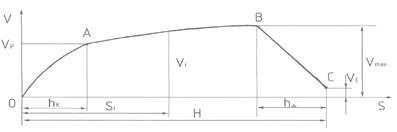
Рисунок 5.1. Фазовая траектория контактных стержней
Здесь обозначено: Vp
- скорость контактных стержней в момент размыкания; hk
- ход в контактах; Vmax
- максимально допустимая скорость контактных стержней; H - полный ход контактных стержней.
На первом участке ОА механизм быстро разгоняется до заданной скорости Vp
, затем с малым ускорением проходит основной участок пути АВ, и наконец, быстро тормозится на участке ВС. Быстрый разгон механизма на участке ОА обеспечивается параллельной работой отключающей и буферной пружин, а быстрое торможение в конце хода контактов – установкой демпфера.
Подобная фазовая траектория может быть получена за счет соответствующего выбора жесткостей Сот
, Сб
и предварительных натягов λо0
и λб0
отключающей и буферной пружин, обеспечивающего выполнение следующих трех условий:
1.Скорость разрыва контактов (точка А) должна быть равна заданной величине Vp
;
2.Максимальная скорость контактов (точка В) не должна превосходить Vmax
;
3.Отключающая пружина должна удерживать подвижные контакты в верхнем положении (точка С), преодолевая силу их веса с некоторым коэффициентом запаса k1.
Примем отношение длин O3
М к O3
Eравным α, и согласно заданию, выберем из конструктивных соображений α=0.4. Тогда
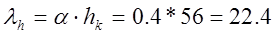 (мм), (5.3) (мм), (5.3)
 (мм) (5.4) где (мм) (5.4) где
λh
– ход отключающей и буферной пружин, соответствующий ходу стержней в контактах, мм;
λоН
– рабочий ход отключающей пружины, соответствующий полному ходу контактных стержней Н, мм.
   
 Выберем коэффициент предварительного натяга буферной пружины Выберем коэффициент предварительного натяга буферной пружины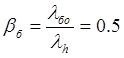 . (5.5) . (5.5)
Тогда величина предварительного натяга буферной пружины λбо
определяется как
 (мм). (5.6) (мм). (5.6)
Задав коэффициент запаса k1
, силу трения в контакте Fk
и силу трения подвижного контакта в уплотнении Fy
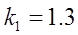 , ,
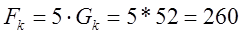 (Н), (5.7) (Н), (5.7)
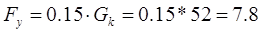 (Н). (5.8) (Н). (5.8)
Вычислим минимально допустимую величину предварительного натяга отключающей пружины
 (5.9) (5.9)
Выберем βо
=0.5. Аналогично параметру βб
определим величину предварительного натяга отключающей пружины λо0
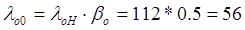 (мм). (5.10) (мм). (5.10)
Находим максимальное и минимально допустимое значение для жесткости отключающей пружины Сот
, Н/м:
 , (5.11) , (5.11)
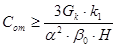 . (5.12) . (5.12)
Подставим в (5.11) и (5.12) численные значения:
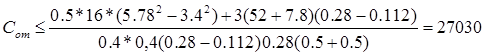 (Н/м), (5.13) (Н/м), (5.13)
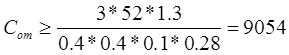 (Н/м). (5.14) (Н/м). (5.14)
Примем Сот
=10000 Н/м.
Тогда жесткость буферной пружины Сб
, определяется из условия
 , (5.15) , (5.15)
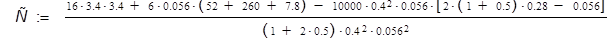
Сб=64890 Н/м.
Примем Сб
=65000 Н/м.
На рисунке 5.2 изображены зависимости усилий, развиваемых отключающей и буферной пружинами, от вертикальной проекции λ перемещения точки М коромысла (рис. 5.1), приближенно совпадающей с изменением длины пружин.
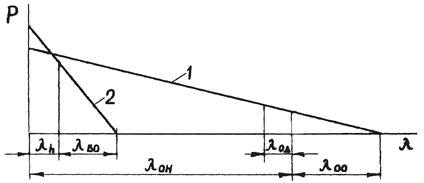    
 Рисунок 5.2. Характеристики отключающей (1) и буферной (2) пружин: λk
– ход отключающей и буферной пружин, соответствующий ходу стержней в контактах; λод
– ход отключающей пружины, соответствующий рабочему ходу штока демпфера; λон
– деформация отключающей пружины, соответствующая полному ходу контактных стержней Н. отсчет координаты λ ведется от верхнего положения точки К.
5.3 Построение фазовой траектории контактных стержней в фазе отключения
В этом разделе строится зависимость скорости контактных стержней V от их перемещения S (рис. 5.1) на участке АВ от момента разрыва контактов до момента встречи коромысла со штоком демпфера. Для этогоразбиваем ход контактов на участке АВ на n=10 частей и вычисляем скорости контактов в конце каждого из участков.
Координата точки А:
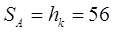 (мм). (5.16) (мм). (5.16)
Координата точки В:
 (мм). (5.17) (мм). (5.17)
Длина участка АВ:
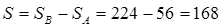 (мм). (5.18) (мм). (5.18)
Длина участка разбиения:
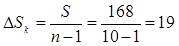 (мм). (5.19) (мм). (5.19)
На основании теоремы об изменении кинетической энергии получаем:
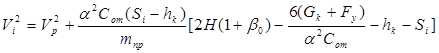 , (5.20) где Vi
– скорость контактов (м/с) на участке Si
; здесь Si
, м определяется по формуле: , (5.20) где Vi
– скорость контактов (м/с) на участке Si
; здесь Si
, м определяется по формуле:
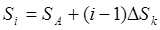 . .
Подставляем численные значения в (5.20):
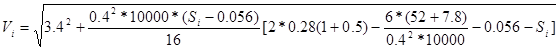 . .
Результаты расчета сводим в таблицу 5.1. Для построения графика фазовой траектории контактных стержней, согласно заданию зададим скорость стержней в конце хода демпфера Vc
=0.3 м/с, также примем перемещение контактных стержней соответствующее ходу демпфера равным hд
=hk=56 мм.
Таблица 5.1. Зависимость скорости контактных стержней V от их перемещения S.
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Si
,м |
0.056 |
0.075 |
0.094 |
0.113 |
0.132 |
0.151 |
0.169 |
0.188 |
0.207 |
0.224 |
| Vi
,м/с |
3.4 |
3.533 |
3.651 |
3.756 |
3.848 |
3.93 |
3.997 |
4.058 |
4.109 |
4.151 |
Полученная зависимость V(S) вплоть до точки В является возрастающей, а скорость контактных стержней в точке В не превышает значения Vmax
:
V(SB
)=4.151 (м/с);
Vmax
=1.7*Vp=1.7*3.4=5.780 (м/с).
Выполнение этих двух условий означает, что величины Сот
и λо0
были найдены верно, и расчет по формуле (5.20) проделан верно.
5.4 Определение времени отключения
Время отключения является одной из важнейших характеристик выключателя. Полное время отключения Т, с складывается из времени отключения на трех участках: ОА, АВ и ВС (см. рис. 5.3)
T=t1
+t2
+t3
, (5.21)
где t1
– время разгона контактных стержней от нулевой скорости до Vр
(участок ОА), с;
t2
– время разгона от момента разрыва контактов до момента встречи коромысла со штоком демпфера (участок АВ), с;
t3
– время торможения (участок ВС), с.
Время разгона контактных стержней от нулевой скорости до Vр
с достаточной степенью точности может быть получено при условии, что ускорение стержней аст
, м/с2
здесь считается постоянным. Это допущение обусловлено тем, что сила действия буферной и отключающей пружин на участке ОА изменяется незначительно. Тогда, получи м
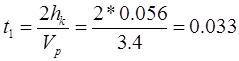 (с). (5.22) (с). (5.22)
Время разгона t2
находим, пользуясь соответствующими точками фазовой траектории, как площадь под графиком V(S). Для этого график V(S) на участке АВ разбивается на n=10 частей.
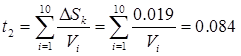 (c), (5.23) (c), (5.23)
где
∆Sk
– длина интервала разбиения, мм;
Vi
– среднее значение скорости на i–ом участке, м/с; значения берутся из табл. 5.1.

Рисунок 5.3. Определение времени отключения
Найдем t3
, с – время торможения до достижения контактными стержнями в конце хода демпфера скорости Vс
. Тогда получим
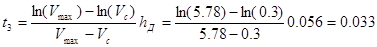 (с). (5.24) (с). (5.24)
Сложив t1
, t2
, t3
получим полное время отключения
T=t1
+t2
+t3
=0.033+0.084+0.033=0.15 (с).
5.5 Приведение масс механизма в фазе включения
Каки в фазе отключения, при определении mпр
, кг можно пренебречь всеми слагаемыми, входящими в правую часть выражения (5.1), кроме слагаемого, содержащего массу контактных стержней. Используя подобное допущение, получим
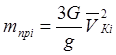 . (5.25) Здесь ṼKi=VKi/Vпр – аналог передаточной функции механизма (табл. 4.1); Vпр равная скорости штока двигателя принимается равной единице. Результаты расчета сведены в таблицу 5.2 и по ним построен график приведенной массы механизма в фазе отключения mпр=f(Sш) (рис. 5.4). . (5.25) Здесь ṼKi=VKi/Vпр – аналог передаточной функции механизма (табл. 4.1); Vпр равная скорости штока двигателя принимается равной единице. Результаты расчета сведены в таблицу 5.2 и по ним построен график приведенной массы механизма в фазе отключения mпр=f(Sш) (рис. 5.4).
Таблица 5.2. Значение приведённой массы механизма в фазе включения.
| i |
1 |
2 |
3 |
4 |
5 |
6к |
6 |
7 |
| mпр,кг |
49.92 |
49.12 |
48.64 |
48 |
48.64 |
48.96 |
49.12 |
49.92 |
5.6 Приведение сил статического сопротивления к штоку двигателя
Условие равенства мощности приведенной к штоку силы Fст сумме мощностей всех сил сопротивления выключателя запишем следующим уравнением:
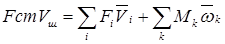 , (5.26) где , (5.26) где
Fj
– статическая сила и силы, приложенная в i-ой точке механизма;
Vj
– скорость точки приложения силы;
Mk
– момент пары сил трения в k-х шарнирах;
ωk
– относительная угловая скорость элементов, сопрягаемых в k-х шарнирах.
Разделив формулу (5.26) на Vш
получим:
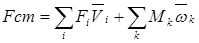 , (5.27) отбросив в формуле (5.26) слагаемые, выражающие работу сил трения, и разделив оставшееся на η, для каждого из семи положений механизма получим: , (5.27) отбросив в формуле (5.26) слагаемые, выражающие работу сил трения, и разделив оставшееся на η, для каждого из семи положений механизма получим:
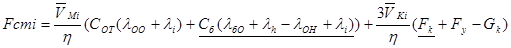 , (5.28) , (5.28)
где ṼMi, ṼKi– определяются на основании таблицы 4.1;
i – номер текущего положения штока;
Fстi - приведенная сила сопротивления, Н;
η – коэффициент полезного действия. Коэффициент η при последовательном соединений кинематических пар определяется выражением:
η=η1*η2*η3…*ηn, (5.29)
где η1,η2,…,ηn - КПД i-ой пары. Примем ηi для подшипника скольжения без постоянной смазки для всех положений одинаковым. Выберем η=0.95. Тогда общий КПД всего механизма cдевятью кинематическими парами:
η=0.95*0.95*0.95*0.95*0.95*0.95*0.95*0.95*0.95=0.63.
Перемещение λi
определяется выражением:
 , (5.30) где l2
– длина коромысла O3
М; , (5.30) где l2
– длина коромысла O3
М;
θi – текущее значение угла поворота коромысла отчитываемое от положения «отключено».
В соответствии с выражениями (5.30) найдем значения перемещения λ, и занесем их в таблицу 5.3.
Таблица 5.3. Зависимость угла поворота коромысла ЕМ и перемещения λ от положения механизма
| i |
1 |
2 |
3 |
4 |
5 |
6к |
6 |
7 |
| θi
,° |
0 |
7.5 |
15 |
22.5 |
30 |
37 |
37.5 |
45 |
| λi
|
0 |
0.019 |
0.038 |
0.057 |
0.077 |
0.095 |
0.096 |
0.115 |
Подчёркнутые в (5.28) слагаемые не учитываются лишь в том случае, если подвижный контакт не замкнут с неподвижным контактом, а рычаг О3К не касается буферной пружины. Этому соответствует положение механизма (6к). В положении 6к проводят два вычисления Fст по формуле (5.28), без учёта подчёркнутых слагаемых и с учётом. Произведя расчет Fст(Sш
), сведем полученные данные в таблицу 5.4 и построим график функции Fст(Sш
) (рис. 5.5).
Таблица 5.4. Зависимость приведённой силы сопротивления от положения штока
| i |
1 |
2 |
3 |
4 |
5 |
6к0 |
6к |
7 |
8 |
| Sш
,мм |
0 |
15 |
31 |
47.5 |
64 |
76 |
76 |
80 |
95 |
| Fст, Н |
543 |
937 |
1315 |
1611 |
2126 |
2520 |
8569 |
9225 |
11970 |
5.7 Выбор силовой характеристики двигателя
   
 Очевидно, что включение выключателя произойдет лишь в том случае, если работа двигателя на участке пути от начала движения до любого промежуточного положения будет не меньше работы сил сопротивления на этом же участке пути. В начальной фазе движения для того, чтобы механизм тронулся с места и разогнался до некоторой скорости, движущие силы FД1 должны быть больше сил сопротивления FСТ1. В дальнейшем для того, чтобы обеспечить безударное торможение, большими должны стать силы сопротивления. Запишем соотношение для случая Sш
= Sш0
: Очевидно, что включение выключателя произойдет лишь в том случае, если работа двигателя на участке пути от начала движения до любого промежуточного положения будет не меньше работы сил сопротивления на этом же участке пути. В начальной фазе движения для того, чтобы механизм тронулся с места и разогнался до некоторой скорости, движущие силы FД1 должны быть больше сил сопротивления FСТ1. В дальнейшем для того, чтобы обеспечить безударное торможение, большими должны стать силы сопротивления. Запишем соотношение для случая Sш
= Sш0
: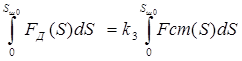 , (5.31) где k3
– коэффициент запаса, гарантирующий включение механизма в случае непредвиденного увеличения сил сопротивления или уменьшения движущих сил по сравнению с номинальными. Зададим k3
=1.05; , (5.31) где k3
– коэффициент запаса, гарантирующий включение механизма в случае непредвиденного увеличения сил сопротивления или уменьшения движущих сил по сравнению с номинальными. Зададим k3
=1.05;
Sшо – полный ход перемещения штока.
Представим линейную характеристику движущих сил в виде:
FД=F1*(1+K*Sш/Sшо). (5.32)
Выполняя интегрирование в левой и правой части уравнения (5.31) получим:
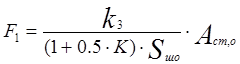 , (5.33) , (5.33)
где 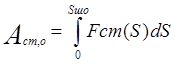 - работа сил статических сопротивлений на полном ходе штока, которая определяется численно как площадь под графиком зависимости Fст=f(Sш) (рис.5.5); - работа сил статических сопротивлений на полном ходе штока, которая определяется численно как площадь под графиком зависимости Fст=f(Sш) (рис.5.5);
К – угловой коэффициент наклона характеристики движущих сил двигателя. К=0.2.
Подставив численные значения в формулу (5.32) найдем значения силы, развиваемой двигателем и занесём их в таблицу значений для силы, развиваемой двигателем (табл. 5.5), построим график зависимости FД(Sш
) (рис. 5.5).
Таблица 5.5. Зависимость силы, развиваемой двигателем, от положения штока
| Sш
, мм |
0 |
15 |
31 |
47.5 |
64 |
76 |
80 |
95 |
| FД, Н |
1519 |
2168 |
2764 |
3474 |
4056 |
4512 |
4785 |
5321 |
5.8 Построение фазовой траектории контактных стержней в фазе включения
Для построения фазовой траектории, используем теорему об изменении кинетической энергии системы:
 (5.34) (5.34)
где mПР,i, Vшi – приведённая масса и скорость штока в i – ый момент времени.
Из выражения (5.34) найдём скорость штока:
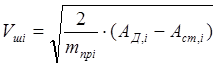 (5.35) (5.35)
где АД,iи Aст,i– работы сил двигателя и статических сил на перемещении штока, которые определяются численно, как площадь под соответствующим графиком FД=f(Sш) и Fст=f(Sш).
Результаты вычислений по формуле (5.35) заносят в таблицу 5.6, и строится график Vш=f(Sш) (рис.5.6).
Основными кинематическими характеристиками являются скорость контактных стержней и их перемещения. Строим график зависимости Vст=f(Sk). Для i-го положения механизма скорость стержня:
VK,i=ṼK,i*Vш,i,
для перемещения:
SK,i=f(Sш,i),
где ṼK,iи соотношения перемещения SK,i=f(Sш,i),берутся из таблицы 4.1.
График фазовой траектории контактных стержней при включении представлен на рисунке 5.6.
Таблица 5.6. Зависимость работы сил сопротивления, сил двигателя, скорости штока, скорости перемещения контактных стержней от положения механизма
| № п.п |
1 |
2 |
3 |
4 |
5 |
6к |
6 |
7 |
| mпр, кг |
49.92 |
49.12 |
48.64 |
48 |
48.64 |
48.96 |
49.12 |
49.92 |
| Fст, Н |
543 |
937 |
1315 |
1611 |
2126 |
2520 |
9225 |
11970 |
| 8569 |
| Fд, Н |
1519 |
2168 |
2764 |
3474 |
4056 |
4512 |
4785 |
5321 |
| Аст, Дж |
0 |
11.1 |
28.8 |
51 |
85 |
116 |
152 |
311 |
| Ад, Дж |
0 |
27.7 |
66 |
118.6 |
178.4 |
229 |
252 |
324.5 |
| Vш, м/с |
0 |
0.82 |
1.237 |
1.678 |
1.96 |
2.148 |
2.018 |
0.735 |
| Vст, м/с |
0 |
2.56 |
3.8 |
5.1 |
5.88 |
6.57 |
6.2 |
2.3 |
5.9 Определение времени включения
Время включения определяем, используя фазовую траекторию движения штока Vш=f(Sш) (рисунок 5.6), аналогично тому, как это было сделано в разделе 5.4 при определении времени t2 прохождения контактными стержнями участка АВ. Для вычисления времени включения весь ход штока разобьём на 10 равных частей. В результате получим:
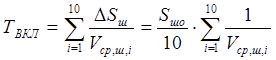 , (5.36) , (5.36)
где Vср,ш,i– среднее значение скорости на этом участке.
 с с
|