 Дано: Дано:
 (см)
; (см)
;
 (см)
; (см)
;
 (см)
; (см)
;
 (кН)
; (кН)
;
Найти:
реакции опор конструкции.
Решение
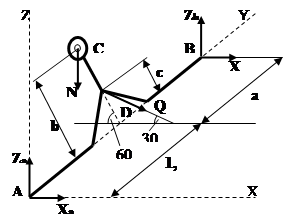
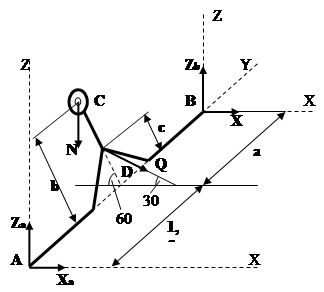
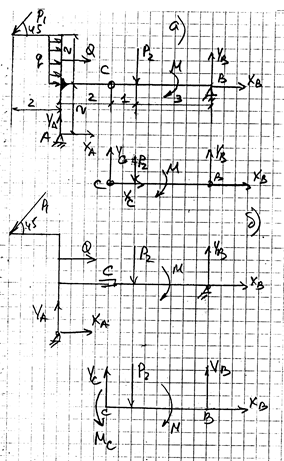
Обозначим на следующем рисунке реакции опор нашей конструкции.
 Fkx
=0 (1) Fkx
=0 (1)
Fky
=0 (2)
Fkz
=0 (3)
mx
(Fk
)=0 (4)
my
(Fk
)=0 (5)
mz
(Fk
)=0 (6)
(1) XA
+XB
+Qcos30 =0
(3) ZA
+ZB
-Qsin30-N =0
(4) ZB*
2,5a-N*1,5a-Qsin30*1,5a=0
(5) – N*b*cos60+Q*c*sin30=0
(6) – XB*
2,5a-Qcos30*1,5a=0
(6) – XB*
2,5–2cos30*1,5=0
XB
=-2cos30*1,5 / 2,5 =0 => XB
= -1,039 kH
(1) XA
+XB
+Qcos30 =0
XA
=1,039 -2cos30 =0 => Xa = -0,693 kH
(5) – N*b*cos60+Q*c*sin30 =0
N=2*30*sin30 / 60*cos60 =0 => N = 1 kH
(4) ZB*
2,5a-N*1,5a-Qsin30*1,5a =0
ZB
=(1*1,5a+2sin30*1,5a) / 2,5a =0 => ZB
= 1,2 kH
(3) ZA
+ZB
-Qsin30-N =0
ZA
=-1,2+2sin30+1 =0 => Za = 0,8 kH
 Проверка: Проверка:
mx1
(Fk
)=0
– ZA*
2,5a+N*a+Qsin30*a=0
-0,8*2,5+1+2*0,5=0
0=0 – верно
mz1
(Fk
)=0
XA*
2,5a+Qcos30*a=0
-0,693*2,5+2*0,866=0
0=0 – верно.
| Силы
, k
Н
|
| XA
|
ZA
|
XB
|
ZB
|
N |
| -0,693 |
-0,8 |
-1,039 |
1,2 |
1 |
Задание
: найти реакции опор конструкции
Дано:
| Q |
G |
a |
b |
c |
R |
r |
| 3 kH |
2 kH |
60 см |
20 см |
40 см |
20 см |
5 см |
Найти реакции опор А и В.
Для нахождения искомых величин, которых, как видно из конструкции, четыре: XA
, XB
, ZB
, ZA
– запишем систему из 5 уравнений, характеризующих условия равновесия механизма:
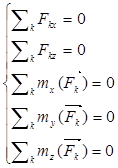
Уравнение проекций сил на ось Oy отсутствует за неимением первых.
 В данной конструкции действующая сила натяжения нити может быть заменена на силу. В этой ситуации будет учитываться и груз, прикреплённый к нити В данной конструкции действующая сила натяжения нити может быть заменена на силу. В этой ситуации будет учитываться и груз, прикреплённый к нити
Спроектируем силы и перепишем систему:

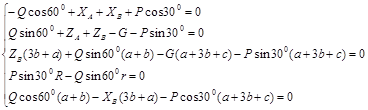
Получилась система из 5 уравнений с пятью неизвестными, решая которую, получим:
| XA
Н
|
XB
Н
|
ZA
Н
|
ZB
Н
|
PН
|
| 330,45 |
44,55 |
-2191 |
2242 |
1299 |
Получилось, что реакция опоры ZA
– отрицательна. Это означает, что на рисунке она должна быть направлена в другую сторону. Решение для модулей выглядит следующим образом:
| XA
Н
|
XB
Н
|
ZA
Н
|
ZB
Н
|
PН
|
| 330,45 |
44,55 |
2191 |
2242 |
1299 |
Ответ: XA
=330,45 Н; XB
=44,55 Н; ZB
=2242 Н; ZA
=2191 Н.
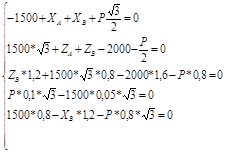 XA
Н XA
Н
|
XB
Н
|
ZA
Н
|
ZB
Н
|
PН
|
| 716,5 |
134 |
-1658 |
1435 |
750 |
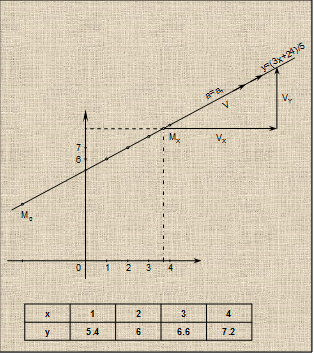
1. Исключим время t из уравнений:
t=y/5 ________
x=7 (y/5) 2
-3 или y=√25 (x+3)/7 – полупарабола вдоль оси ОХ
2. Определение скорости:
VX
=x1
=14tПри t1=1/4 cVx =14/4=3.5 (см/с)
Vy
=y1
=5=const
________ ______
V=√V2
x+V2
y=√3.52
+52
= 6.1 (см/с)
3. Определение ускорений:
ax
=x11
=14 (см/с2
)=const
ay
=y11
=0 (см/с2
)
______
 a=√a2
x+a2
y= √142
+0 =14 (см/с2
) a=√a2
x+a2
y= √142
+0 =14 (см/с2
)
Тангенциальное ускорение:
aτ
=(Vx
*ax
+Vy
*ay
)/V= (3.5*14+5*0)/6.1 = 8,03 (см/с2
)
_________
 an
=√a2
-a2
τ=√142
– (8.03)2
= 11.5 (см/с2
) an
=√a2
-a2
τ=√142
– (8.03)2
= 11.5 (см/с2
)
ρ=V2
/an
=(6.1) 2
/11.5= 3.24 (см/с2
)
xt1=5t2
+5t/3–3=-2.56 (см)
yt1=3t2
+t+3=7 (см)
Mt
1
(-2.56; 1.25) – положение точки при t=t1
M0
(-3; 0) – положение в начальный момент времени


Дано: R2
=40; r2
=20; R3
=35; r3
=35
X=C2
t2
+C1
t+C0
При t=0 x0
=7  =6 =6
t2
=2 x2
=103 см
X0
=2C2
t+C1
C0
=7
C1
=6
103=C2
*22
+6*2+7
4C2
=103–12–7=84
C2
=21
X=21t2
+6t+7
 =V=42t+6 =V=42t+6
a= =42 =42
V=r2
 2 2
R2
 2
=R3 2
=R3
 3 3
 3
=V*R2
/(r2
*R3
)=(42t+6)*40/20*35=2,4t+0,34 3
=V*R2
/(r2
*R3
)=(42t+6)*40/20*35=2,4t+0,34
 3
= 3
= 3
=2,4 3
=2,4
Vm
=r3
* 3
=35*(2,4t+0,34)=84t+11,9 3
=35*(2,4t+0,34)=84t+11,9
at
m
=r3

 =2,4t =2,4t
at
m
=R3
 =35*2,4t=84t =35*2,4t=84t
an
m
=R3
 2
3
=35*(2,4t+0,34)2
=35*(2,4 (t+0,14)2 2
3
=35*(2,4t+0,34)2
=35*(2,4 (t+0,14)2
a=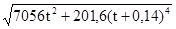
|