| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИНСТИТУТ БИЗНЕСА И ПРАВА
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра "Экономика и менеджмент"
А.В. Чернова
И.А. Краснобокая
АНАЛИЗ ПОКАЗАТЕЛЕЙ РЯДА ДИНАМИКИ
Методические указания по выполнению лабораторной работы
Дисциплина - "Статистика"
Специальность - 060400 "Финансы и кредит"
060500 "Бухгалтерский учет, анализ и аудит"
060800 "Экономика и управление на предприятиях
туризма и гостиничного хозяйства"
061000 "Государственное и муниципальное управление"
061100 "Менеджмент организации"
061500 "Маркетинг"
351000 "Антикризисное управление"
351200 "Налоги и налогообложение"
Печатается по решению редакционно-издательского совета Орел ГТУ
Орел 2003
Авторы: профессор кафедры экономики и менеджмента, доктор экономических наук А.В. Чернова, старший преподаватель кафедры экономики и менеджмента, кандидат экономических наук И.А. Краснобокая
Рецензент: заведующий кафедрой экономики и менеджмента, профессор, доктор экономических наук С.А. Никитин
Методические указания по выполнению лабораторной работы содержат рекомендации и задания по расчету и анализу показателей рядов динамики. Предназначены для студентов специальностей 060400 "Финансы и кредит", 060500 "Бухгалтерский учет, анализ и аудит", 061000 "Государственное и муниципальное управление", 060800 "Экономика и управление на предприятиях туризма и гостиничного хозяйства", 061100 "Менеджмент", 061500 "Маркетинг", 351000 "Антикризисное управление", 351200 "Налоги и налогообложение" при изучении дисциплины "Статистика".
Редактор
Технический редактор
Орловский государственный технический университет
Лицензия ИД №00670 от 05.01.2000 г.
Подписано к печати. .03 г. Формат 60х84 1/16.
Печать офсетная. Уч. изд. л. Усл. печ. л.,. Тираж 300 экз.
Заказ №
Отпечатано с готового оригинал-макета на полиграфической базе ОрелГТУ, 302030, г. Орел, ул. Московская, 65.
Орел ГТУ, 2003
Чернова А.В., Краснобокая И.А., 2003
Содержание
1. Методические указания по выполнению лабораторной работы
2. Пример выполнения лабораторной работы
3. Задание и порядок выполнения лабораторной работы
Рекомендуемая литература
Приложение
Задача изучения изменения анализируемых показателей во времени решается при помощи построения и анализа рядов динамики (временных рядов).
Ряд динамики (динамический ряд) представляет собой ряд числовых значений статистического показателя, расположенных в хронологической последовательности и характеризующих изменение социально-экономических явлений во времени.
В каждом ряду динамики имеются два основных элемента: уровни динамического ряда (обозначаются "Y") и период времени, за который они представлены ("t").
В зависимости от времени, отраженному в динамических рядах, они разделяются на моментные и интервальные.
Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенную дату (момент) времени. Например, ряд, характеризующий динамику численности постоянного населения по состоянию на первое января каждого года.
Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, месяц, квартал). Например, ряд, характеризующий динамику выпуска продукции за каждый месяц отчетного года.
Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики, которая может быть представлена следующей группой показателей: абсолютный прирост; темп (коэффициент) роста; темп (коэффициент) прироста; абсолютное значение одного процента прироста.
В основе расчета показателей рядов динамики лежит сопоставление его уровней. В зависимости от применяемого способа сопоставления (базисный или цепной) показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
Для расчета показателей на постоянной базе (базисный способ расчета) каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. И показатели называются цепными.
Абсолютный прирост характеризует абсолютную скорость роста или снижения сравниваемых уровней, и рассчитывается как разность между последующим и предыдущим уровнем, принятым за базу сравнения. Измеряется в тех же единицах, что и исходная информация.
А = Y1
- Y0
, (1)
где Y1
- значение отчетного уровня ряда динамики;
Y0
- значение базисного уровня ряда динамики.
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени.
Темп (коэффициент) роста характеризует относительную скорость роста или снижения уровней ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в процентах, а коэффициент роста - в долях.
 , (2), , (2),  . (3) . (3)
Между цепными и базисными коэффициентами роста существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному темпу роста последнего периода; частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Темп (коэффициент) прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения:
 , (4) , (4)
 . (5) . (5)
Абсолютное значение одного процента прироста определяется отношением абсолютного прироста к темпу прироста, и показывает, сколько единиц в абсолютном выражении приходится на один процент прироста для данного ряда динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он будет постоянной величиной:
 . (6) . (6)
Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Существуют две категории этих показателей:
1) средние уровни ряда;
2) средние показатели динамики данного ряда.
Метод расчета среднего уровня динамического ряда зависит от вида временного ряда.
В интервальных рядах динамики
из абсолютных уровней средний уровень определяется по формуле средней арифметической:
простой (при равных интервалах):
 , (7) , (7)
где  - сумма абсолютных уровней ряда; - сумма абсолютных уровней ряда;
n - число уровней.
взвешенной (при неравных интервалах):
 , (8) , (8)
где Y - уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;
t - длительность интервалов времени (дней, месяцев) между смежными датами.
Для моментного ряда
средний уровень определяется с помощью средней хронологической:
простой (для ряда динамики с равностоящими уровнями)
 , (9) , (9)
где Y - уровни периода, за который делается расчет;
m - число уровней.
взвешенной (для ряда динамики с неравностоящими уровнями):
 , (10) , (10)
где Yi
, Yn
- уровни ряда динамики;
t - интервал времени между уровнями.
При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период с более или менее стабильными условиями развития. Если же за исследуемый период можно выделить этапы, в течение которых условия развития существенно менялись, то пользоваться общей средней не всегда целесообразно, а предпочтение нужно отдать средним, рассчитанным по отдельным периодам.
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При базисном способе расчета, чтобы определить средний абсолютный прирост, для этого определяется разность между конечным Уn
и базисным У0
уровнями изучаемого периода, которая делится на m-1 субпериодов:
 , (11) , (11)
где m - число уровней ряда динамики в изучаемом периоде, включая базисный. При цепном способе расчета для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
 , (12) , (12)
где n - число цепных абсолютных приростов в изучаемом периоде.
Средний темп (коэффициент) роста является обобщающей характеристикой индивидуальных темпов (коэффициентов) роста ряда динамики. Для базисного способа расчета средний темп (коэффициент) роста будет определяться по формуле:
 , (13) , (13)
 . (14) . (14)
Для определения среднего темпа (коэффициента) роста цепным способом применяется формула средней геометрической:
 100, (15) 100, (15)
 , (16) , (16)
где Кр1
, Кр2
,..., Кр
n
- индивидуальные (цепные) коэффициенты роста;
n - число индивидуальных темпов роста
Средний темп (коэффициент) прироста рассчитывается на основе средних темпов (коэффициентов) роста по следующим формулам:
 , (17), , (17),  . (18) . (18)
Среднее значение одного процента прироста определяется только для цепного способа расчета по формуле:
 . (19) . (19)
Данные показатели динамики находят практическое применение во всех расчетах, где требуется изучение изменения социально-экономических явлений во времени.
Задание на лабораторную работу.
Исходя из данных об объёмах производства продукции промышленными предприятиями области необходимо:
2.1 Определить следующие аналитические показатели ряда динамики цепным и базисным способами: а) абсолютные приросты; б) темпы роста и прироста; в) абсолютное значение 1% прироста; г) средние обобщающие показатели ряда динамики.
Результаты расчётов представить в таблице.
2.2 Проверить взаимосвязь между цепными и базисными абсолютными приростами, темпами роста.
2.3 Построить график динамики производства продукции промышленными предприятиями области по рассчитанным базисным темпам роста.
2.4 Проанализировать полученные данные.
Решение:
Построим таблицу 1 "Динамика производства продукции промышленными предприятиями области за 1993-2002 гг."
Таблица 1 - Динамика производства продукции промышленными предприятиями области за 1993-2002 гг.
| Год
|
Объём производства продукции, млн. руб.
|
Абсолютный прирост, млн. руб.
|
Темп роста,%
|
Темп прироста,%
|
Абсолютное значение 1% прироста, млн. руб.
|
| базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
| 1993
|
10,0
|
-
|
-
|
100
|
100
|
-
|
-
|
-
|
| 1994
|
10,7
|
0,7
|
0,7
|
107
|
107
|
7
|
7
|
0,1
|
| 1995
|
12,0
|
2,0
|
1,3
|
120
|
112,1
|
20
|
12,1
|
0,107
|
| 1996
|
10,3
|
0,3
|
-1,7
|
103
|
85,8
|
3
|
-14,2
|
0,12
|
| 1997
|
12,9
|
2,9
|
2,6
|
129
|
125,2
|
29
|
25,2
|
0,103
|
| 1998
|
16,3
|
6,3
|
3,4
|
126,3
|
126,4
|
26,3
|
26,4
|
0,129
|
| 1999
|
15,6
|
5,6
|
-0,7
|
156
|
95,7
|
56
|
-4,3
|
0,163
|
| 2000
|
17,8
|
7,8
|
2,2
|
178
|
114,1
|
78
|
14,1
|
0,156
|
| 2001
|
18,0
|
8,0
|
0,2
|
180
|
101,1
|
80
|
1,1
|
0,178
|
| 2002
|
18,7
|
8,7
|
0,7
|
187
|
103,9
|
87
|
3,9
|
0,18
|
Рассчитаем средний уровень динамики ряда по формуле (7):
 (млн. руб.) (млн. руб.)
Рассчитаем следующие показатели:
а) средние абсалютные приросты:
базисный, по формуле (11):
 (млн. руб) (млн. руб)
цепной, по формуле (12):
 (млн. руб.). (млн. руб.).
б) темпы роста и прироста:
базисный, по формуле (13)
 % %
цепной, по формуле (15):
 % %
Рассчитаем средний темп прироста по формуле (17):
 % %
 %. %.
в) абсолютное значение 1% прироста по формуле (19):
Среднее значение 1% прироста (только цепной способ):
1% =  (млн. руб.). (млн. руб.).
Проверим взаимосвязь между цепными и базисными абсолютными приростами и темпами роста:
между абсолютными приростами:
А94/93
+ А95/94
+ А96/95
+ А97/96
+ А98/97
+ А99/98
+ А00/99
+ А01/00
+ А02/01
= =А02/93
0,7 + 1,3 - 1,7 + 2,6 + 3,4 - 0,7 + 2,2 +0,2 + 0,7 = 8,7 (млн. руб.)
8,7 = 8,7 (млн. руб.)
между темпами роста:
а) k94/93
· k95/94
· … · k02/01
= kр02/93
1,07 · 1,121 · 0,858 · 1,252 · 1,264 · 0,95 · 1,141 · 1,011 · 1,039 = 1,87%
1,87 = 1,87
б) Например, k 1995:

 % %
112,1 = 112,1.
Построим график динамики производства продукции по рассчитанным базисным темпам роста:
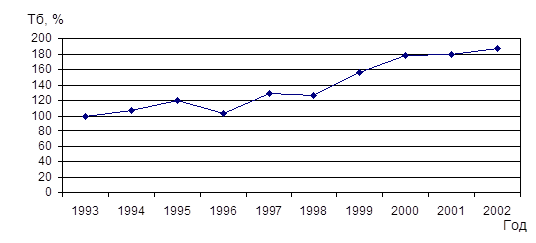
Рисунок 1 - График динамики производства продукции промышленными предприятиями области по рассчитанным базисным темпам роста.
Вывод. Проанализировав рисунок 1, можно сделать вывод о том, что наблюдается тенденция к росту производства продукции, в основном. Однако, в 1996 и 1998 годах наблюдался спад производства. В среднем за период с 1993 по 2002 годы объём производства за год составил 14,23 млн. руб., увеличился за отчётный период на 0,97 млн. руб. (средний абсолютный прирост) и составил 7,2% (средний темп роста).0,13 млн. руб. составили 1% прироста в среднем.
Исходя из данных своего варианта об объемах производства продукции промышленными предприятиями области (таблица 1) необходимо:
3.1 Определить следующие аналитические показатели ряда динамики цепным и базисным способом:
а) абсолютные приросты;
б) темпы роста и прироста;
в) абсолютное значение одного процента прироста;
г) средние обобщающие показатели ряда динамики.
Результаты расчетов представить в таблице 2.
3.2 Проверить взаимосвязь между цепными и базисными абсолютными приростами, темпами роста.
3.3 Построить график динамики производства продукции промышленными предприятиями области по рассчитанным базисным темпам роста.
3.4 Проанализировать полученные данные.
Таблица 2 - Производство продукции промышленными предприятиями области за 1993 - 2002 г.г.
| Год
|
Объем производства продукции, млн. руб.
|
| В А Р И А Н Т Ы
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
|
10,0
10,7
12,0
10,3
12,9
16,3
15,6
17,8
18,0
18,7
|
10,0
10,5
11,9
10,3
12,9
16,3
15,8
17,5
18,0
18,7
|
10,2
10,8
12,0
10,3
12,0
16,2
15,5
17,8
18,2
18,9
|
10,4
10,7
12,0
10,5
12,0
16,0
15,6
17,2
18,5
19,0
|
10,0
10,7
12,0
10,3
12,8
16,5
15,6
17,8
18,1
18,7
|
10,2
10,8
11,8
10,4
12,3
15,9
15,8
17,5
18,2
19,0
|
10,0
10,7
12,0
10,3
12,8
16,1
15,5
17,7
18,0
18,8
|
10,1
10,5
12,1
10,4
12,0
16,1
15,6
17,8
18,0
18,7
|
10,0
10,7
12,0
10,4
12,9
16,2
15,5
17,8
17,9
18,5
|
10,0
10,8
11,9
10,3
12,8
16,3
15,6
17,6
18,1
18,5
|
Таблица 3 - Динамика производства продукции промышленными предприятиями области за 1993 - 2002 г. г.
| Год
|
Объем производства продукции, млн. руб.
|
Абсолютный прирост, млн. руб.
|
Темп роста, %
|
Темп прироста, %
|
Абсолютное значение 1% прироста, млн. руб.
|
| базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
| 1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
|
10,0
10,7
12,0
10,3
12,9
16,3
15,6
17,8
18,0
18,7
|
|
|
|
|
|
|
|
1. Гусаров В.М. Статистика: Учеб. пособие для вузов. - М.: ЮНИТИ-ДАНА, 2002. - 463 с.
2. Ефимова М.Р. и др. Практикум по общей теории статистики: Учеб. пособие / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова. - М.: Финансы и статистика, 2000. - 280 с.
3. Практикум по статистике: Учеб. пособие для вузов / Под ред. В.М. Симчеры / ВЗФЭИ. - М.: ЗАО "Финстатинформ", 1999. - 259 с.
4. Статистика: Учеб. пособие / Под ред. проф. М.Р. Ефимовой. - М.: ИНФРА-М, 2002. - 336 с.
5. Теория статистики: Учебник / Под ред. Г.А. Громыко. - М.: ИНФРА-М, 2000. - 414 с.
6. Теория статистики: Учебник / Под ред.Р.А. Шмойловой. - 2-е изд., доп. и перераб. - М.: Финансы и статистика, 1998. - 576 с.
7. Чернова А.В. Теория статистики: Учебное пособие по курсу "Статистика". Ч.1 (для студентов экономических специальностей) / Орел ГТУ, 1997. - 101 с.
8. Чернова А.В. Статистика промышленности: Учебное пособие по курсу "Статистика". Ч.2 (для студентов экономических специальностей) / Орел ГТУ. Каф. "ЭиМ". - Орел, 1998. - 114 с.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИНСТИТУТ БИЗНЕСА И ПРАВА
Кафедра "Экономика и менеджмент"
ЛАБОРАТОРНАЯ РАБОТА
по дисциплине "Статистика"
на тему: "Анализ показателей ряда динамики"
Выполнил студент:
Группа:
Специальность:
Руководитель лабораторной работы:
Оценка защиты:
Орел 2003
|