|
3.5.1.
Периодические смещения ядер молекулы относительно некоторых равновесных положений называют молекулярными колебаниями. Этот вид внутримолекулярного движения при некоторых упрощениях можно представить в виде совокупности однономерных движений, каждому из которых отвечает своя колебательная степень свободы.
3.5.2.
Пространственным перемещениям центра масс молекулы отвечают 3 поступательные степени свободы. Движениям ее как целого относительно центра масс соответствуют вращательные степени свободы. Их число определяется минимально необходимым количеством плоских поворотов, требуемых для перевода молекулы в любую пространственную ориентацию относительно закрепленной системы координат, исходящей из центра масс. У молекулы с нелинейной равновесной геометрией ядерного остова таких поворотов 3 и столько же вращательных степеней свободы, а у молекул с линейной геометрией – достаточно лишь двух поворотов и вращательных степеней свободы две.
Всего же внешних механических степеней свободы, к которым относятся поступательные и вращательные, у молекул либо 6, либо 5. Если молекула содержит N
-атомов, то для полного механического описания ядерных перемещений требуется 3N
степеней свободы и на долю колебательных остается 3N-6
у нелинейных молекул и 3
N
-5
у линейных.
3.5.3.
Простейшая, очень эффективная модель молекулярного одномерного колебания описывает колебание гармоническое, называемое линейным вибратором
или линейным осциллятором
. Для простоты, далее везде будем называть его просто осциллятором, за исключением специально оговариваемых ситуаций.
Из элементарной физики известно, что гармонические колебания классической системы порождаются упругой силой, линейно зависящей от смещения колеблющейся массы относительно равновесного положения, т.е. 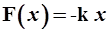 (сила Гука). Потенциальная энергия упругих сил квадратично зависит от смещения: (сила Гука). Потенциальная энергия упругих сил квадратично зависит от смещения:
 . (3.70) . (3.70)
Напомним также, что константа упругости k
связана с колеблющейся приведенной массой μ
и собственной круговой частотой ω
формулой
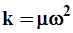 , где , где 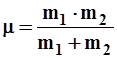 , (3.71) , (3.71)
так что потенциальная энергия имеет вид:
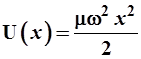 . (3.72) . (3.72)
3.5.4.
Решение уравнение Шредингера для гармонического осциллятора довольно сложно и требует специальных сведений из теории дифференциальных уравнений, хотя при этом не добавляется качественно новой информации по сравнению с задачами “ящика” и “ротатора”. Возможен иной, значительно более простой путь расчета уровней и волновых функций осциллятора, основанный на использовании только элементов алгебры операторов. Этот путь основан на совместном анализе уравнения Шредингера (колебательного гамильтониана) и коммутационного соотношения Гейзенберга (3.67). При этом мы получаем возможность как бы “пересчитывать” уровни и состояния, “перемещаясь” по их лесенке, с помощью специально вводимых операторов сдвига
уровней-состояний.
3.5.5.
Итак, рассмотрим систему операторных выражений, а именно:
гамильтониан  , (3.73) , (3.73)
коммутационное соотношение 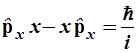 . (3.73а) . (3.73а)
Введем подстановки, не влияющие на смысл формул, а лишь изменяю-щие “масштабы” переменных
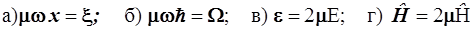 . (3.74) . (3.74)
Умножая выражение (3.73) на 2μ
, а (3.73а) на μω
и используя подста-новки (3.74), можно упростить формулы (3.73) и (3.73а)
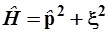 , (3.75) , (3.75)
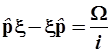 , (3.76) , (3.76)
и для любого из дискретных уровней с номером υ
уравнение Шредингера при-обретает вид:
 . (3.77) . (3.77)
3.5.6.
Гамильтониан (3.75) представлен в виде суммы квадратов двух операторов  и и 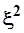 , связанных коммутационным соотношением (3.76). Используя схему алгебры комплексных чисел (см. раздел 1.3.2
.), попытаемся разложить гамильтониан (3.75) на сомножители, содержащие только первые степени составляющих его операторов , связанных коммутационным соотношением (3.76). Используя схему алгебры комплексных чисел (см. раздел 1.3.2
.), попытаемся разложить гамильтониан (3.75) на сомножители, содержащие только первые степени составляющих его операторов
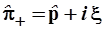 , (3.78) , (3.78)
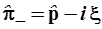 . (3.79) . (3.79)
3.5.7.
Произведения комплексных чисел коммутативны, поэтому безразличен порядок записи комплексно-сопряженных сомножителей:
(a + ib
) (a - ib
) = (a - ib
) (a + ib
) = C·C* =|C|2
.
(3.80)
Так как операторы не обладают свойством коммутативности следует ожидать, что операторные произведения 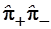 и и 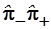 различны и не равны гамильтониану, поэтому требуется исследовать их связь с гамильтонианом. При этом следует помнить, что в силу линейности операторов, слагаемые операторных сумм можно переставлять, а отдельные группы сомножителей можно объединять, так как операторные произведения обладают свойством ассоциативности. различны и не равны гамильтониану, поэтому требуется исследовать их связь с гамильтонианом. При этом следует помнить, что в силу линейности операторов, слагаемые операторных сумм можно переставлять, а отдельные группы сомножителей можно объединять, так как операторные произведения обладают свойством ассоциативности.
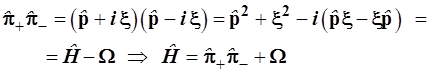 , (3.81) , (3.81)
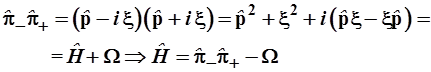 . (3.82) . (3.82)
Таким образом, произведения операторов 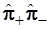 и и 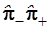 отличаются от гамильтониана на постоянную величину отличаются от гамильтониана на постоянную величину 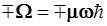 соответственно. соответственно.
Подставим найденные в (3.81) и (3.82) выражения гамильтониана в уравнение Шредингера (3.77) и перенесем постоянные множители в правую часть полученных уравнений :
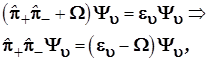 (3.83) (3.83)
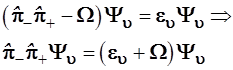 (3.84) (3.84)
3.5.8.
Для выяснения смысла операторов 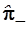 и и 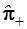 еще раз подействуем первым из них на обе части уравнения (3.83), а вторым – на уравнение (3.84), т.е. домножим эти уравнения слева на еще раз подействуем первым из них на обе части уравнения (3.83), а вторым – на уравнение (3.84), т.е. домножим эти уравнения слева на 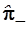 и и 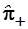 соответственно: соответственно:
 , (3.85) , (3.85)
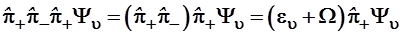 . (3.86) . (3.86)
Подставим вместо произведений операторов (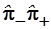 ) и ( ) и (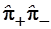 ) их выражения (3.82) и (3.81) и опять перенесем постоянные величины Ω
в правую часть уравнений: ) их выражения (3.82) и (3.81) и опять перенесем постоянные величины Ω
в правую часть уравнений:
 (3.87) (3.87)
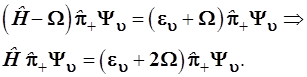 . (3.88) . (3.88)
В итоге каждое из уравнений (3.87) и (3.88) приобрело стандартный вид уравнения Шредингера, но собственные функции в них (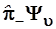 ) и ( ) и (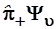 ) отличны от волновой функции исходного состояния Ψ
υ
, а собственные значения ) отличны от волновой функции исходного состояния Ψ
υ
, а собственные значения 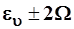 отличаются от исходного ευ
на постояннуювеличину. Функции ( отличаются от исходного ευ
на постояннуювеличину. Функции (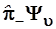 ) отвечает уровень ) отвечает уровень 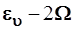 , на величину 2Ω сдвинутый вниз по отношению к уровню состояния Ψ
υ
, т.е. оператор , на величину 2Ω сдвинутый вниз по отношению к уровню состояния Ψ
υ
, т.е. оператор 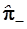 произвел понижение уровня на один номер: произвел понижение уровня на один номер:
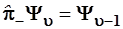 . (3.89) . (3.89)
Аналогично оператор 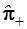 сдвигает номер уровня и состояния Ψ
υ
на еди- ницу вверх: сдвигает номер уровня и состояния Ψ
υ
на еди- ницу вверх:
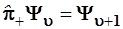 . (3.90) . (3.90)
Функции 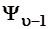 и и  , полученные с помощью операторов , полученные с помощью операторов 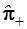 и и 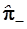 по формулам (3.89) и (3.90), не нормированы; но в дальнейших расчетах это несу-ественно. Состоянию по формулам (3.89) и (3.90), не нормированы; но в дальнейших расчетах это несу-ественно. Состоянию 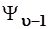 отвечает уровень отвечает уровень  , а , а  – уровень – уровень 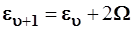 , т.е. , т.е.
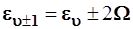 . (3.91) . (3.91)
3.5.9.
Переход к обычной энергетической шкале с использованием подста-новок (3.74б и 3.74в) дает
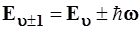 . (3.92) . (3.92)
Согласно формуле (3.92), уровни гармонического осциллятора эквидис-тантны
, и интервал между.ними равен 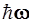 . .
3.5.10.
Продолжая исследование лесенки уровней, учтем, что сверху она неограничена, но нижняя граница определена уровнем основного состояния Ψ0
, ниже которого не существует состояний системы. Поэтому попытка подействовать оператором понижения 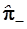 на волновую функцию основного состояния должна дать нулевой результат, т.е. применительно к волновой функции основного уровня оператор понижения сыграет роль ее “уничтожителя” – аннигилятора: на волновую функцию основного состояния должна дать нулевой результат, т.е. применительно к волновой функции основного уровня оператор понижения сыграет роль ее “уничтожителя” – аннигилятора:
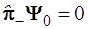 (3.93) (3.93)
Здесь целесообразно вернуться к переменной х
. С учетом выражения для 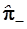 (3.80) и подстановки (3.74а) формулу (3.93) после простых преобразований приводим к дифференциальному уравнению для (3.80) и подстановки (3.74а) формулу (3.93) после простых преобразований приводим к дифференциальному уравнению для 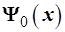 : :
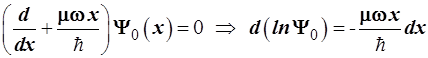 , (3.94) , (3.94)
при интегрировании которого получим волновую функцию основного состояния:
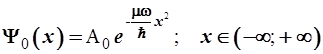 . (3.95) . (3.95)
Далее находим нормировочный множитель А0
:
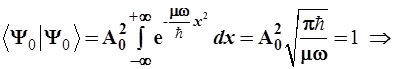 (3.96) (3.96)
 . (3.97) . (3.97)
При раскрытии выражения (3.96) использован интеграл Пуассона:
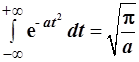 . .
3.5.11.
Волновая функция  является собственной функцией гамильто-ниана. Поэтому для расчета основного уровня достаточно подействовать по-следним на является собственной функцией гамильто-ниана. Поэтому для расчета основного уровня достаточно подействовать по-следним на и определить собственное значение и определить собственное значение
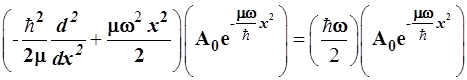 (3.98) (3.98)
Энергия искомого основного уровня равна 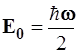 . (3.99) . (3.99)
Последовательными сдвигами на 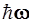 вверх, согласно уравнению (3.92), получается вся лесенка энергетических уровней, и схема квантования энергии осциллятора передается формулой:
вверх, согласно уравнению (3.92), получается вся лесенка энергетических уровней, и схема квантования энергии осциллятора передается формулой:
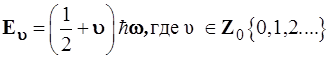 (3.100) (3.100)
3.5.12.
Оператор повышения 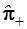 позволяет получить весь спектр волновых функций из позволяет получить весь спектр волновых функций из  . Если υ
раз подействовать оператором . Если υ
раз подействовать оператором 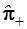 на на  , то получится , то получится с точностью до постоянного множителя. Иными словами, генератор волновой функции υ
-го состояния – это оператор повышения, возведенный в степень υ
: с точностью до постоянного множителя. Иными словами, генератор волновой функции υ
-го состояния – это оператор повышения, возведенный в степень υ
:
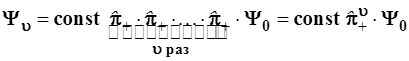 . (3.101) . (3.101)
Напомним, что любое преобразование волновой функции, в общем случае, порождает необходимость новой нормировки.
3.5.13.
Обсудим вид волновых функций осциллятора. Для этого удобно произвести еще одно упрощение за счет замены переменной путем подстановки:
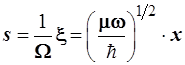 , (3.102) , (3.102)
благодаря чему 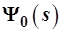 и оператор повышения и оператор повышения 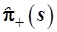 , необходимый для полу-чения , необходимый для полу-чения 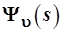 , примут вид: , примут вид:
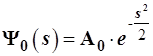 , (3.103) , (3.103)
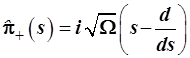 . (3.104) . (3.104)
Постоянный коэффициент в выражении (3.104) ие играет роли, так как к функции Ψ
υ
, генерируемой по формуле (3.105), он добавляет лишь множитель 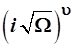 , который далее автоматически входит в состав нормировочного множителя А
υ
, и поэтому Ψ
υ
передается формулой: , который далее автоматически входит в состав нормировочного множителя А
υ
, и поэтому Ψ
υ
передается формулой:
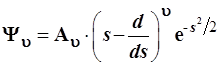 (3.105) (3.105)
Оператор 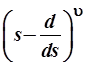 представляет собой бином, составленный из степеней переменной s
и оператора дифференцирования представляет собой бином, составленный из степеней переменной s
и оператора дифференцирования  , который в свою очередь извлекает из гауссовой экспоненты , который в свою очередь извлекает из гауссовой экспоненты 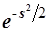 степенные множители, в результате выражение (3.105) преобразуется к виду: степенные множители, в результате выражение (3.105) преобразуется к виду:
 , (3.106) , (3.106)
где 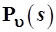 – многочлен степени υ, называемый полиномом Эрмита
. Нетрудно убедиться, что эти полиномы можно представить выражением, которое легко запоминается, благодаря своей симметричности: – многочлен степени υ, называемый полиномом Эрмита
. Нетрудно убедиться, что эти полиномы можно представить выражением, которое легко запоминается, благодаря своей симметричности:
 . (3.107) . (3.107)
Последовательно придавая υ значения 0, 1, 2, 3 …, читатель легко может вывести формулы полиномов Эрмита разных порядков. Для того, чтобы читатель смог проверить свои расчеты, приведем в табл.2 несколько первых полиномов Эрмита вместе с их корнями и графиками. В табл.2 также изображены графики ненормированных волновых функций
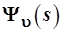 =. =.
У волновых функций имеется один и тот же множитель – экспонента 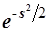 ; эта быстро спадающая к нулю функция при удалении от начала координат “прижимает” к оси абсцисс расходящиеся было ветви полиномов. В результате получается картина, очень напоминающая поведение волновых функции “ящика”. ; эта быстро спадающая к нулю функция при удалении от начала координат “прижимает” к оси абсцисс расходящиеся было ветви полиномов. В результате получается картина, очень напоминающая поведение волновых функции “ящика”.
Табл.2.
Полиномы Эрмита и волновые функции гармонияеского
осциллятора
| υ
|
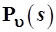 |
Корни полиномов |
Графики полиномов |
Графики волновых функций 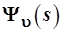 . . |
| 0 |
1 |
- |
| 1 |
2s
|
0 |
| 2 |
4s
2
- 2 |
±1/√2 |
| 3 |
8s
3
- 12 s
|
0; ±3/2 |
| 4 |
16s
4
-48s
2
+12 |
±0,525; ±1,651 |
Читатель может сам получить формулу для нормировочных коэффициентов или взять их готовое выражение:
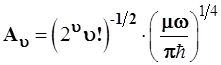 . (3.108) . (3.108)
3.5.14.
Прямыми вычислениями нетрудно еще раз проверить свойство ортогональности волновых функций. Интегрирование по всей области возможных значений переменной х
дает:
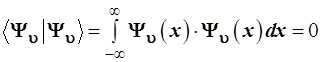 , (3.109) , (3.109)
что наглядно видно из графиков табл. 2
Напомним, что свойство ортогональности – это общее свойство собствен-ных функций любого эрмитова оператора, к числу которых относится и гамильтониан.
3.5.15.
Все полиномы Эрмита и порождаемые ими волновые функции делятся на два класса – четные и нечетные. Ранее подобное свойство наблюдалось у волновых функций “ящика” и “ротатора”. Анализ четности волновых функций и их произведений оказывается очень полезным при оценке различных характеристик системы. Рассмотрим это на примерах.
Покажем, что среднее отклонение колеблющейся системы от положения равновесия равно нулю. Следуя 5-му постулату, запишем для υ
=
0:
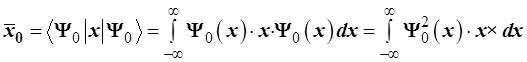 . (3.110) . (3.110)
Подинтегральное выражение нечетное, так как образовано в виде произве-дения по правилу (чет × нечет × чет)
. Интеграл, взятый в симметричных пределах от нечетной функций, тождественно равен нулю, так что 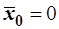 . Это же имеет место и для других состояний. . Это же имеет место и для других состояний.
3.5.16.
Иначе обстоит дело со среднеквадратичным отклонением 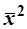 , на-зываемым среднеквадратичной амплитудой осциллятора. Произведем соответ-ствующие расчеты; вновь обращаясь к 5-му постулату: , на-зываемым среднеквадратичной амплитудой осциллятора. Произведем соответ-ствующие расчеты; вновь обращаясь к 5-му постулату:
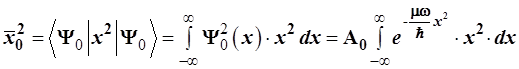 , (3.111) , (3.111)
 (3.112) (3.112)
В преобразовании (3.112) использован табличный интеграл
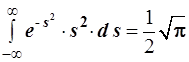 . (3.113) . (3.113)
3.5.17.
Сравним среднеквадратичное отклонение 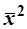 с квадратом ампли-туды, предсказываемой на основе формулы, связывающей классическое и квантово-механическое выражение для полной энергии: с квадратом ампли-туды, предсказываемой на основе формулы, связывающей классическое и квантово-механическое выражение для полной энергии:
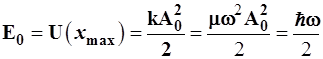 , (3.114) , (3.114)
откуда 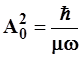 и и  . (3.115) . (3.115)
Формулы (3.112) и (3.115) практически дают один и тот же результат, поскольку классическая амплитуда А0
– это максимальное отклонение осциллятора от положения равновесия, тогда как квадратичная “амплитуда” 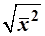 усреднена по всем положениям осциллятора, а понятие точной траектории и предельного отклонения не имеет смысла в квантовой механике. усреднена по всем положениям осциллятора, а понятие точной траектории и предельного отклонения не имеет смысла в квантовой механике.
Можно показать, что соответствие классической амплитуды и квантово-механического среднеквадратичного отклонения сохраняется и в других состояниях осциллятора, а именно:
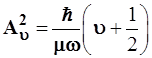 и и 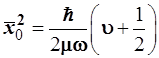 (3.120) (3.120)
(в квазиклассическом подходе) (в квантовомеханическом подходе)
3.5.18.
Среднеквадратичные амплитуды играют важную роль в экспериментах, связанных с определением равновесных положений ядер в молекулах, например, в электронографии или в рентгеноструктурном анализе. Они также позволяют на основе опытных колебательных спектров (инфракрасного поглощения и комбинационного рассеяния) определить пределы изменения молекулярных “размеров” за счет колебательных деформаций ядерного остова молекулы.
3.6. Сравнение свойств “ящика”, “ротатора” и осциллятора.
3.6.1.
Три рассмотренные модели простейших одномерных движений в ограниченном пространстве позволяют проследить некоторые общие качественные закономерности, касающиеся состояний и уровней квантово-механических систем. Они наглядно проявляются при сопоставлении энергетических диаграмм и графиков волновых функций “частицы в ящике”, “гармонического осциллятора” и “плоского ротатора”.
3.6.2.
В первом случае потенциальная энергия нулевая на выделенном интервале, и, как говорят, потенциальная “яма” имеет прямоугольную форму. Во втором случае потенциальная энергия изменяется квадратично при отклонении от равновесия и говорят о параболической форме потенциальной “ямы”. Наконец, ротатор отсутствием потенциальной энергии напоминает “ящик”. Отсюда, хотя способы нумераций уровней и отличаются, схемы квантования энергии у этих систем одинаковы – уровни расходятся с возрастанием квантового числа.
У гармонического осциллятора квантование энергии уникально – уровни эквидистантны. Благодаря этому при взаимодействии с квантами света частота поглощаемого излучения совпадает с собственной частотой молекулярного осциллятора, например, колеблющихся атомов, связанных химической связью.
Таким образом, квантование полной энергии системы определяется потенциальной функцией.
3.6.3.
В разделе 3.2.5. мы связали вырождение уровней ротатора с равноправием двух направлений вращения вокруг оси. Можно высказать еще и более общее утверждение, связывающее наличие вырождения с порядком вращательной оси системы. Плоский ротатор – это система с осью вращения бесконечного порядка. Далее будет показано, что вырожденные уровни появляются у систем, имеющих ось третьего порядка и выше.
В целом же, нам удалось приобрести некоторые необходимые навыки в решении простейших задач квантовой механики.
|