| Содержание
Введение
1. Разработка АСУ ТП холодильной установки
1.1 Техническое задание и технико-экономическое обоснование
1.1.1 Техническое задание на проектирование АСУ ТП
1.1.2 Технико-экономическое обоснование
1.2 Структурная идентификация объекта
1.3 Математическая модель объекта
1.3.1 Ограничения в модели объекта
1.4 Построение статических характеристик объекта
1.5 Выбор критерия оптимизации
1.6 Экстремальные характеристики зависимости целевой функции от управлений
1.7 Алгоритм оптимизированного управления
1.8 Структура двухуровневого управления
1.9 Структура алгоритма адаптивного управления
1.10 Краткое описание, структура и состав алгоритмического, программного и технического обеспечения АСУ
1.11 Выбор и обоснование используемых технических средств
1.12 Описание функциональной схемы АСУ
2. Календарное планирование производства
2.1 Постановка задачи
2.2 Решение задачи
3. Исследование технических объектов как систем массового обслуживания
Заключение
Список использованной литературы
Введение
В данном курсовом проекте рассматривается АСУ ТП холодильной установки, аналитически выводится математическая модель объекта, рассматриваются статические характеристики объекта относительно управляющих и возмущающих воздействий в области существующих ограничений, выбирается и обосновывается критерий оптимизации на основе одного из технико-экономических показателей; обосновывается оптимальный режим работы холодильной установки для данного ТП, приводится структура двухуровневого управления с координирующей подсистемой на верхнем уровне и блок-схема алгоритма ее функционирования; составлена структура и блок-схема алгоритма адаптивного управления.
В данном проекте производится решение конкретной задачи календарного планирования и находится оптимальная последовательность обработки деталей в смысле критерия минимального времени обработки всей партии.
Приводится исследование технического объекта как системы массового обслуживания, находится оптимальная загрузка системы.
1 Разработка АСУ ТП холодильной установки
1.1 Техническое задание и технико-экономическое обоснование
Сущность процесса заключается в том, что в холодильную камеру помещают продукт, поступающий на предприятие от поставщиков. В холодильной камере продукт охлаждают от начальной температуры, около 70 °С до температуры tk
=(-18) °С ±3 °С. Затем продукт поступает на длительное хранение в специально оборудованные холодильные камеры или поступают на погрузку в рефрижераторы автомобильного или железнодорожного транспорта для транспортировки.
1.1.1
Техническое задание на проектирование АСУ ТП
Основанием для проектирования АСУ ТП холодильной установки является задание на курсовую работу.
Объектом автоматизации является холодильная установка, включая холодильную камеру и находящиеся в ней ресурсы.
Необходимо разработать схему автоматизации, позволяющую сократить время технологического процесса и обеспечивающую комфортные условия для контроля параметров ТП.
Необходимо поддерживать 100% заполнения испарителя жидким хладагентом. Температура охлажденного продукта должна быть равной tk
=(-18) °С ±3 °С. Давление в конденсаторе должно быть равно Pk
=Pk
0
.
Давление в циркуляционном ресивере должно составлять Р = Р0
.
Уровень заполнения циркуляционного ресивера должен составить 0,3 Нцр
,
где Нцр
- высота циркуляционного ресивера.
Система должна иметь двухуровневую структуру управления с координирующей подсистемой на верхнем уровне.
1.1.2
Технико-экономическое обоснование
Рассматриваемая АСУ ТП холодильной установки позволяет сократить время технологического процесса за счет того, что в условиях работы АСУ ТП автоматически поддерживается 100% заполнение испарителя жидким хладагентом, что позволяет поддерживать в холодильной камере минимальную температуру, что сокращает время протекания теплообменного процесса за счет низкой температуры испарителя.
Комфортные условия контроля технологических параметров обеспечиваются благодаря тому, что информация от датчиков поступает на программируемый контроллер SIMATIC S7-200, где происходит ее обработка.
Технико-экономические показатели сравниваемых вариантов представлены в таблице 1.1.
Таблица 1.1. Технико-экономические показатели сравниваемых вариантов.
| Показатели
|
Варианты сравнения
|
| Базовый
|
Проектир.
|
| 1 Производительность кг/ч
|
1500
|
1500
|
| 2 Время действия оборудования в течении года ,ч
|
10000
|
8000
|
| 3 Число обслуживающего персонала
|
4 чел
|
1 чел
|
| 4 Расход на единицу пр-ции электроэнергии, кВтх ч воды , м3
|
10010
|
5810
|
| 5 Стоимость единицы : электроэнергии , руб/кВтх ч воды, руб/м3
|
24
|
24
|
| 6 Себестоимость единицы продукции , руб/кг
|
100
|
133
|
| 7 Годовой выпуск продукции , кг
|
15000000
|
12000000
|
В процессе расчета были получены следующие данные:
-годовая экономия от снижения себестоимости продукции составила 936000 руб.;
-годовой экономический эффект составляет 746673,15 руб.
Срок окупаемости затрат составляет примерно 168 дня при капитальных вложениях на создание и внедрение АСУТП 430288,29 руб.
В результате оптимального управления процессом себестоимость единицы продукции (1 кг) снизилась с 0,195 руб (до внедрения проектируемой АСУТП) до 0,117 руб (после внедрения АСУТП).
1.2 Структурная идентификация объекта
На объект охлаждения, холодильную камеру, действует тепловой поток Qo
6
,
приходящий с продуктом, помещенным в холодильную камеру.
Холодильная машина должна отвести от холодильной камеры тепловой поток Qn
,
причем так, чтобы параметры рабочей среды поддерживались в заданных пределах. Холодильная машина выполняет работу, потребляя энергию Е от внешнего источника для вывода тепла Qe
в охлаждающую среду.

Рисунок 1.1 – Функциональная схема холодильной установки
ХМ - холодильная машина,
ХК - холодильная камера,
Qo
б
- тепловой поток продукта в холодильной камере;
Qn
- тепловой поток, отводимый холодильной машиной от холодильной камеры;
Е - энергия потребления ХМ;
Q
в
-
тепло, отводимое ХМ от ХК в окружающую среду
1.3 Математическая модель холодильной камеры
Математическая модель взята из книги Канторовича В.И. «Автоматизации холодильных установок» М.:«Агропромиздат», 1987г., с. 136.
При выводе модели объекта использовались следующие допущения:
а) Считаем, что утечка тепла через стенки холодильной камеры не происходит.
б) Считаем, что температура в холодильной камере распределена равномерно по всему объему камеры.
в) Считаем, что продукт до момента помещения его в холодильную камеру имел температуру, равную температуре окружающей среды (Q
в
).
г) Считаем, что температура воздуха окружающей среды постоянна. Тогда уравнение теплового баланса будет иметь вид:
Qп
– Qоб
= 0 (1.1)
Значение теплового потока, отводимого от ХК (
Qn
)
в Дж/с, рассчитываем по формуле:
Qп
= kп
Fп
(Qп
- Qоб
) (1.2)
где kп
– коэффициент теплопередачи испарителя, Дж/(м2
×0
С×с),
Fп
– площадь теплопередающей поверхности испарителя, м2
.
Значение теплового потока, приходящего в ХК (
qo
6
)
в Дж/с, рассчитываем по формуле
Qоб
= kоб
Fоб
(Qоб
- Qв
) (1.3)
где kоб
– коэффициент теплопередачи продукта, Дж/(м2
×0
С×с),
Fп
– площадь теплопередающей поверхности, м2
.
Запишем уравнение (1.1) для рассматриваемого процесса в динамике, в приращениях:
d
DQ
0
= (
DQn
-
DQo
б
)
dt
,
(1.4)
где DQ
0
-
количество тепла, необходимого для восстановления теплового баланса за время dt, записанное в приращении, Дж.
Значение (DQ
0
) найдем по формуле:
DQ
0
=cmDQоб
, (1.5)
где с - удельная теплоемкость продукта, Дж/(кг×0
С),
m - масса продукта, кг,
DQоб
- приращение температуры, на которое нужно изменить
температуру продукта, чтобы сохранить тепловой баланс, °С.
Подставляя в (1.4) выражения (1.2), (1.3), (1.5) получим
 (1.6) (1.6)
В выражение (1.6) было подставлено значение
 (1.7) (1.7)
После некоторых преобразований запишем уравнение (1.6) в другом виде:
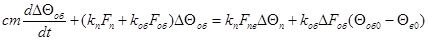 (1.8) (1.8)
Обозначим:
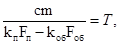 
 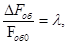 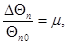 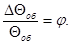
С учетом принятых обозначений выражение (1.8) примет вид:
 (1.9) (1.9)
Для нахождения численных значений параметров модели используем данные из книги Канторовича В.И. «Автоматизации холодильных установок», и рассчитаем значения коэффициентов модели объекта.
Подставим следующие значения в формулы расчета значений Т, kl
, k2
:
 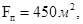  
 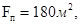  
Тем самым получим значения коэффициентов:
Т = 43,45; kl
= -1,22; k2
= 0,02.
Подставляя полученные значения в выражение (1.9) получим модель объекта

1.3.1 Ограничения в модели объекта
По техническим данным холодильной камеры она не может вместить продукты, площадь (площадь теплопередающей поверхности) которых больше 200 м2
. Здесь сделано допущение, что продукт можно делить и занимать им всю полезную площадь камеры. Тогда запишем ограничение по площади теплопередающей поверхности продукта, которая может измениться от 0 до 200 м.
0 ≤ Fоб
≤ 200 м2
(1.10)
Температура в испарителе не может быть ниже Qп
min
= - 30 °С. Это обусловлено техническими характеристиками холодильной машины и хладагента. Таким образом:
Qп
≥ -30 °С (1.11)
1.4 Построение статических характеристик объекта
Построим статические характеристики объекта относительно управляющих и возмущающих воздействий в области существующих ограничений. Управляющим воздействием в данном случае является температура в испарителе, а возмущающим воздействием является площадь теплопередающей поверхности продукта, т.е. если мы изменяем количество продукта, находящегося в холодильной камере, мы тем самым изменяем среднюю температуру продукта. Здесь не рассматривается случай, когда изменяют площадь теплопередающей поверхности путем перестановке продукта в холодильнике.
Для построения статических характеристик объекта, рассмотрим уравнение (1.1) и подставим в него выражение (1.2) и (1.3), получим
 (1.12) (1.12)
Выразим величину Qоб
, получим:
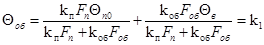 (1.13) (1.13)
где 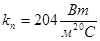 - по техническим характеристикам холодильной камеры, - по техническим характеристикам холодильной камеры,
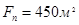
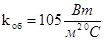 - по справочным данным, - по справочным данным,
 - принимаем сами. - принимаем сами.
Рассчитаем статические характеристики объекта по формуле (1.13) для значений Qп01
= -30°С, Qп02
=-25°С, Qп03
=-200
С, т.е. при различных  значениях управляющего воздействия. Результаты приведены в таблице (1.1) значениях управляющего воздействия. Результаты приведены в таблице (1.1)
Таблица 1.1 – Статические характеристики объекта
| Qп01
= -30°С
|
Qп02
=-25°С
|
Qп03
=-200
С
|
| Fоб
, м2
|
Qоб
, 0
С
|
Fоб
, м2
|
Qоб
, 0
С
|
Fоб
, м2
|
Qоб
, 0
С
|
| 0
|
-30
|
0
|
-25
|
0
|
-20
|
| 25
|
-28,6
|
25
|
-23,7
|
25
|
-18,9
|
| 50
|
-27,3
|
50
|
-22,6
|
50
|
-17,8
|
| 75
|
-26,1
|
75
|
-21,4
|
75
|
-16,8
|
| 100
|
-24,9
|
100
|
-20,4
|
100
|
-15,9
|
| 125
|
-23,7
|
125
|
-19,4
|
125
|
-15,0
|
| 150
|
-22,7
|
150
|
-18,4
|
150
|
-14,1
|
| 175
|
-21,7
|
175
|
-17,5
|
175
|
-13,3
|
| 200
|
-20,7
|
200
|
-16,6
|
200
|
-12,6
|
Графическое представление статических характеристик объекта относительно управляющих и возмущающих воздействий в области существующих ограничений приведено на рисунке 1.2

Рисунок 1.2- Статические характеристики объекта
Статические характеристики объекта линейны так как, температура в испарителе напрямую зависит (по формуле 1.13) от площади продукта, которую мы равномерно повышаем.
1.5 Выбор критерия оптимизации и целевой функции управления
Результатом внедрения АСУ ТП холодильной установки является сокращение времени технологического (контроля) процесса охлаждения продукта.
Известно, что чем ниже будет поддерживаться температура в холодной камере, тем быстрее можно будет охладить продукт до заданной температуры.
Это можно увидеть, проанализировав формулу (1.2). Очевидно, что чем больше будет разница между температурой в испарителе и температурой продукта, тем больше количество тепла отводиться от холодильной камеры в единицу времени, а следовательно быстрее охлаждается продукт. Давление кипения Ро
определяет температуру кипящей жидкости, т.е. температуру хладагента в испарителе Qп
. Другими словами существует зависимость:
 (1.14) (1.14)
Большему давлению Ро
соответствует большая температура Qп
, поэтому чтобы снизить температуру Qп
„ необходимо поддерживать низкое давление Ро.
Минимальное значение Ро
зависит от технических возможностей компрессора. Чем выше хладопроизводительность компрессора, тем более низкую температуру кипения хладагента он может поддерживать.
Из приведенных выше рассуждений можно сделать вывод, что управляющим воздействием является хладопроизводительность компрессора, и целесообразно выбрать критерий
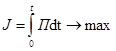 (1.15) (1.15)
где П – производительность установки.
Уменьшая время технологического процесса и сохраняя объем охлаждаемого продукта за цикл охлаждения, мы тем самым повышаем производительность холодильной установки, т.е. увеличиваем объем охлаждаемой продукции за год. Целью повышения производительности установки является снижение себестоимости единицы продукции.
Очевидно, что производительность установки будет зависеть от хладопроизводительности компрессора, тем выше будет его стоимость, следовательно, большей будет сумма амортизационных отчислений, а значит и себестоимость продукции.
Доход предприятия рассчитывается по формуле
D = Пр
– С – Н (1.16)
где Пр
- выручка предприятия от реализации продукции за год, в руб.,
С - себестоимость продукта, в руб.,
Н - налоги, в руб.
Себестоимость продукции в свою очередь складывается из затрат на охлаждение продукта и затрат на амортизационные отчисления.
С = С1
+ А (1.17)
где С1
- затраты на охлаждение продукта, на сырье, з/п и т.д., в руб.,
А - амортизационные отчисления на холодильное оборудование, в руб.
Следовательно доход предприятия будет зависеть от амортизационных отчислений, и чем больше сумма отчислений, тем меньше доход предприятия.
Тогда целевая функция примет вид
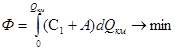 (1.18) (1.18)
где dQ
км
- хладопроизводительность компрессора холодильной машины, кВт.
1.6 Экстремальные характеристики зависимости целевой функции от управлений
Изменение хладопроизводительности компрессора происходит в диапазоне от 0 до 120 кВт, что соответствует техническим особенностям компрессора.
Амортизационные отчисления на холодильное оборудование составляют 11,5% от полной его стоимости. Значение стоимости оборудования взяты из справочных данных [1], расчет затрат на охлаждение продукта произведен аналитическим способом. График целевой функции приведен на рисунке 1.3
График зависимости дохода предприятия от хладопроизводительности компрессора построен на основе формулы (1.16), считая, что значение Пр
и Н не зависят от хладопроизводительности компрессора.
Экстремумы зависимостей D(Qкм
) и C(Qкм
) совпадают, что свидетельствует о целесообразности выбранного критерия. Из графика видно, что оптимальная хладопроизводительность компрессора составляет 58 кВт.
На рисунке 1.3 приведена зависимость целевой функции от хладопроизводительности компрессора, но выше приводились рассуждения на основании которых можно сделать вывод, что значение управления Qп
зависит от хладопроизводительности компрессора, т.е.
Qп
=
f
1(
Q
км
)
(1.19)

Рисунок 1.3 - Графическое изображение целевой функции
На рисунке 1.3: Д – доход предприятия, определяется по формуле (1.16), Ф – целевая функция, А – амортизационные отчисления, С1 – затраты на охлаждение продукта, на сырьё, з/п и т.д.
1.7 Алгоритм оптимизированного управления
Для нахождения оптимального значения хладопроизводительности необходимо знать зависимость изменения температуры хладагента от давления кипения.
Оптимальная задача в данном случае состоит в том, чтобы поддержать максимальную хладопроизводительность компрессора при наименьшей температуре кипения. Контроллер осуществляет расчет системы уравнений, состоящей из уравнения экспериментальной кривой и температурой задания, и находит минимальное значение температуры кипения. После чего формирует закон регулирования.

Рисунок 1.4 - Алгоритм оптимизированного управления
1.8 Структура двухуровневого управления
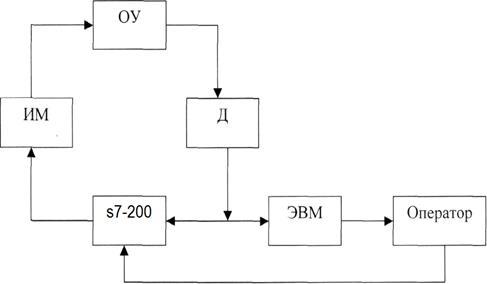
Рисунок 1.5 - Структура двухуровнего управления. Режим советчика.
ОУ - объект управления; Д - датчик; s7-200 - ПМК; ИМ - исполнительный механизм; ЭВМ - вычислительная машина; Оператор - оператор ЭВМ.
Необходимость двухуровневого управления в режиме советчика заключается в том, что велика вероятность ошибки, а также по желанию заказчика, требуется непосредственный контроль человека. Но система способна функционировать и автономно.
Информация о состоянии объекта от датчиков поступает на s7-200, где она обрабатывается и в качестве рекомендаций выдается информация об изменении управления или корректировки. Оператор анализирует полученную информацию и принимает меры по изменению управляющих воздействий.
Блок-схема алгоритма функционирования двухуровнего управления с кординирующей подсистемой на верхнем уровне приведена на рисунке 1.6
На рисунке 1.6 температура Т1 - это температура на выходе из испарителя, а Т2 - температура на входе в испаритель. Для регулирования наполнения испарителя хладогеном, устанавливается регулятор перегрева (ТРВ), который представляет собой П - регулятор. При уменьшении заполнения испарителя перегрев пара на выходе возрастает и ТРВ автоматически увеличивает подачу хладагента. Температура Т1
=
Q
п
= -
30°С.
Испаритель наполнен (100%) жидким хладагентом, если Т1
= Т2
.
В случае если равенство не выполняется, то необходимо изменить настройку ТРВ.
Т3
-
температура объекта (продукта),
Т3
= Qп
= -20°С, если продукт еще не охладился до температуры Т3
процесс продолжается, в противном случае выдается сообщение о том, что технологический процесс окончен и необходимо выгружать продукт и размораживать установку.
Т4
- температура в холодильной камере, °С;
P
1
- давление в конденсаторе, кПа;
Р2
- давление в ЦР, кПа;
Н - уровень заполнения циркуляционного ресивера, м.
Уровень жидкости в циркуляционном ресивере (Н) должен быть в пределах 0,2 ÷ 0,3 высоты ресивера. При повышении уровня жидкость может попасть в компрессор, а при снижении - нарушается подача в испаритель

| Рисунок 1.6 - Блок-схема алгоритма функционирования 2-уровнего управления
|
|
1.9 Структура алгоритма адаптивного управления
Для данной системы управления, в которой свойства холодильной установки можно считать не изменяющимися во времени, т.к. площадь теплопередающей поверхности испарителя не меняется, коэффициент теплопередачи испарителя тоже не меняется во времени. Но так как изменяться во времени может коэффициент теплопередачи продукта, если замораживать различные продукты в каждом цикле охлаждения, а также может изменяться площадь поверхности продукта, если в холодильную камеру загрузили не всю партию продукта, которую она может вместить, а лишь часть ее, необходимо использовать адаптивное управление.
Таким образом, адаптацию можно проводить с каждым циклом охлаждения, зная количество загружаемого продукта в холодильную камеру, т.е. общую площадь теплопередающей поверхности и коэффициент теплопередачи продукта, который зависит от вида продукта. Зная эти данные, можно рассчитать новые коэффициенты в модели объекта, но для достижения максимальной производительности установки, управляющее воздействие должно иметь максимальное значение, т.е. температура в испарителе должна поддерживаться минимальной, не зависимо от свойств продукта и его количества. Поэтому в данном случае алгоритм адаптации будет заключаться лишь в уточнении модели объекта.
Если бы мы имели объект, свойства которого менялись во времени, то к такому объекту можно было бы применить прямой алгоритм адаптации управляющего устройства непосредственно по величине критерия оптимальности.
Положим, что g(t) - полезный задающий сигнал, тогда можно определить рассогласование
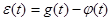 , (1.20) , (1.20)
где 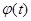 - выход объекта. - выход объекта.
Тогда критерий оптимальности можно записать в виде
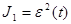 (1.21) (1.21)
Подставив в формулу (1.20) значение j
(
t
)
можно убедиться, что J
1
=
F
(
b
о
),
т.е. является функцией коэффициентов регулятора.
J
1
=
F
(
b
р
)
b
®
min
(1.22)
Другими словами, минимизируя функцию J находим оптимальные коэффициенты регулятора, корректируя которые изменяем управляющее воздействие.
Обобщенная структура системы, реализующей прямой алгоритм адаптации приведена на рисунке 1.7
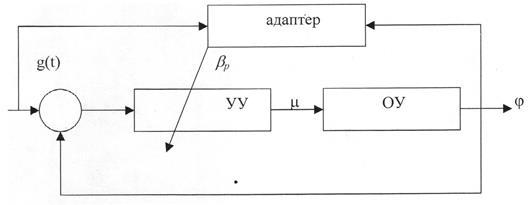
Рисунок 1.7 - Структура адаптивной системы
Под адаптацией подразумевается изменение свойств модели объекта относительно самой системы в процессе протекания технологического процесса. Адаптация происходит следующим образом: на вход управляющего устройства поступает задающий сигнал g(t), после чего снимается значение сигнала на выходе объекта j(t). Адаптер определяет рассогласование e(t) входного и выходного сигнала. Если рассогласование превышает допустимое значение, адаптер изменяет параметры П - регулятора, а именно коэффициент усиления, после чего процесс повторяется.
На рисунке 1.8 приведена блок схема данного алгоритма.
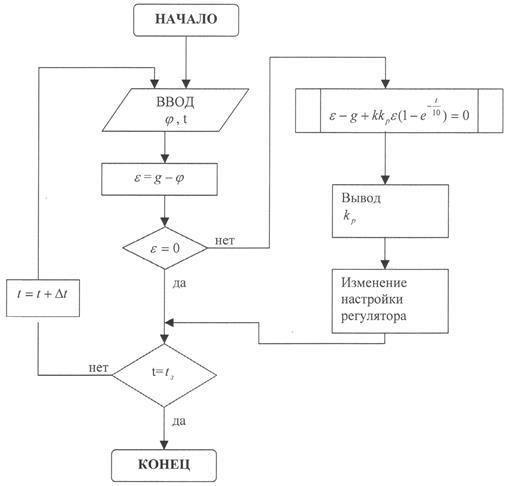
Рисунок 1.8 — Блок-схема прямого алгоритма адаптации
На рисунке 1.8 приведена блок-схема прямого алгоритма адаптации объекта, математическая модель которого может быть представлена дифференциальным уравнением 1-го порядка, а управляющее устройство реализует П - закон регулирования.
1.10 Краткое описание, структура и состав алгоритмического, программного и технического обеспечения АСУ
Рассматриваемая АСУ имеет двухуровневую структуру управления с корректирующей подсистемой на верхнем уровне.
Техническое обеспечение представляет собой комплекс технических средств получения информации о состоянии технологического процесса объекта, к нему относятся датчики, в частности унифицированный датчик давления (МИДА-ДВ-13П) с нормированным выходным сигналом 0..5mA. A также термопреобразователи с унифицированным выходным сигналом (ТХАУ-055, ХА(К)), с нормированным выходным сигналом 0..5mA, у которых в зависимости от температуры среды, изменяется сигнал на выходе. Уровнемер буйковый (УБ-ЭМ1) используется для контроля уровня жидкости в ЦР, с выходным сигналом 0..5mА.
Информационные сигналы поступают на ПМК S7-200, где производиться обработка и отображение на экране монитора ЭВМ в виде численных значений технологических параметров объекта.
Программное обеспечение составляется с помощью пакета STEP 7 MicroWIN. При разработке адаптивного управления использовался прямой алгоритм адаптации, а также разработан специальный алгоритм функционирования двухуровневого управления.
1.11 Выбор и обоснование используемых технических средств
Для обеспечения минимального времени охлаждения продукта необходимо поддерживать минимальную температуру в холодильной камере, которая определяется температурой в испарителе. При заданной хладопроизводительности компрессора мы не можем понизить температуру кипения хладагента. Однако необходимо поддерживать уровень жидкости в испарителе, который должен быть максимальным, чтобы можно было наиболее эффективно использовать его охлаждающую поверхность.
Для регулирования заполнения испарителя хладагентом используем пропорциональный регулятор перегрева, ТРВ (терморегулирующий вентиль).
Выбираем терморегулирующий вентиль DANFOSS TEA 85-85. Для него диапазон изменения температур кипения хладагента составляет (-50÷30)°С, а номинальный режим температуры кипения хладагента Q0
=-30°С, что соответствует техническим характеристикам выбранного компрессора.
Для контроля уровня жидкости в испарителе необходимо знать температуру на выходе из испарителя (Qп вых
) и температуру на входе в испаритель (Qпвх
).
При выполнении равенства
Qпвх
= Qп вых
(1.23)
можно сказать, что испаритель максимально заполнен хладагентом. Для получения информации о температурах Qпвх
и Qп вых
используем термопреобразователь ТХАУ-055, ХА(К), погрешность которого составляет ± 2.5°С, что допустимо для заданной точности регулирования.
Сигнал от термопреобразователя поступает на ПМК S7-200.
Температуру объекта измеряем аналогичным термопреобразователем с погрешностью ±2.5°С допустимой по техническому заданию, т.к. температура объекта должна составлять Qоб
=
(-18°С) ±3°С.
Аналогичный термопреобразователь используется для контроля температуры в холодильной камере.
Давление в конденсаторе Рк
определяется температурой жидкого хладагента. Так как в данном технологическом процессе поддерживается стабильная температура хладагента, то необходимо лишь поддерживать стабильным давление в конденсаторе, поэтому необходимость в автоматическом регулировании отпадает, а для централизованного контроля информацию о значении давления в конденсаторе будем получать используя датчик давления (МИДА-ДВ-13П) с классом точности 1,5, что удовлетворяет необходимой точности контроля.
 Давление кипения P
0
определяет температуру кипящей жидкости Q0
. В данном случае нагрузкой является количество пара, образуемого при кипении хладагента в испарителе, регулирующее воздействие - количество пара, отводимое компрессором. Так как установка работает в одном режиме, т.е. значение нагрузки можно принять постоянным, поэтому можно обойтись ручным регулированием. Давление кипения P
0
определяет температуру кипящей жидкости Q0
. В данном случае нагрузкой является количество пара, образуемого при кипении хладагента в испарителе, регулирующее воздействие - количество пара, отводимое компрессором. Так как установка работает в одном режиме, т.е. значение нагрузки можно принять постоянным, поэтому можно обойтись ручным регулированием.
Для получения информации о значении давления кипения Ро
хладагента используем датчик давления (МИДА-ДВ-13П) с выходным сигналом в диапазоне 0..5mА.
Уровень жидкости в циркуляционном ресивере должен быть в пределах 0,75-0,35 высоты ресивера: при повышении уровня жидкость может попасть в компрессор, а при снижении нарушится подача жидкости в испаритель и может выйти из строя насос. В данном случае нагрузка -количество жидкости, выкипающей в испарителе, регулирующее воздействие - подача жидкости через РВ. В связи с незначительными изменением нагрузки использование автоматического регулирования здесь не целесообразно.
Для измерения уровня используем уровнемер буйковый УБ-ЭМ1. Он имеет унифицированный токовый выходной сигнал, который от уровнемера поступает сразу на S7-200, что повышает точность измерения (класс точности прибора 1,5) и надежность системы в целом, за счет снижения количества приборов (исключаем нормирующие преобразователи).
1.12 Описание функциональной схемы АСУ
Как уже отмечалось выше, система имеет двухуровневую структуру управления с координирующей подсистемой на верхнем уровне.
Для регулирования заполнения испарителя хладагентом применяется пропорциональный регулятор перегрева, называемый терморегулирующим вентилем (1а).
Температура на выходе из испарителя воспринимается термобаллоном манометрической термосистемы. Наполнитель термосистемы выбран таким образом, что когда температура на выходе из испарителя равна температуре кипения хладагента (при 100%-ном заполнении испарителя жидкостью), давление Ртб
= Ро
, где Ртб
-давление в термобаллоне. При выполнении равенства давлений, под действием пружины соответствующий клапан закрывает подачу жидкости из конденсатора в испаритель. При возникновении рассогласования между Ртб
и Ро
клапан открывается.
Для передачи информации об уровне заполнения испарителя на верхний уровень управления: используем два термопреобразователя (2а, За), установленные соответственно на выходе и входе в испаритель. В зависимости от изменения температуры, изменяется электрический выходной сигнал (0..5) mA, затем информация поступает в S7-200, где она обрабатывается и результаты обработки предоставляются оператору.
Температуру продукта измеряем термопреобразователем (4а), выходной сигнал которого (0..5)mА поступает на S7-200, где информация обрабатывается и результаты в виде сообщения об окончании технологического процесса (охлаждения продукта) выдается оператору.
Температуру в холодильной камере измеряем термопреобразователем (5а) сигнал которого (0..5)mА, поступает на вход S7-200, где информация обрабатывается и выдается численное значение температуры в холодильной камере.
Давление в конденсаторе измеряем унифицированным датчиком давления (6а). В зависимости от изменения давления изменяется выходной сигнал датчика (0..5)mА, который поступает на вход S7-200, где обрабатывается и выдается численное значение давления в конденсаторе, которое контролируется оператором.
Давление кипения хладагента измеряем унифицированным датчиком давления (7а). В зависимости от изменения давления изменяется выходной сигнал датчика, который поступает на вход S7-200, где обрабатывается и выдается численное значение давления кипения хладагента.
Для измерения уровня жидкости в циркуляционном ресивере используем буйковый уровнемер (8а) выходной сигнал которого поступает на вход S7-200, где происходит его обработка, после чего выдается значение уровня жидкости в циркуляционном ресивере и рекомендации по его регулированию.
2 Календарное планирование производства
2.1 Постановка задачи
На машиностроительном предприятии имеется два обрабатывающих станка, на которых необходимо обрабатывать 4 детали так, чтобы суммарное время их обработки было минимальным.
Целевая функция для этого случая имеет вид
 (2.1) (2.1)
где ti
,
j
- время обработки на i - станке j – детали.
Даны матрицы последовательности Qi
,
j
(
g
)
и длительности Ti
,
j
(
ti
,
j
)
обработки деталей
 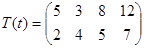
Таким образом мы имеем задачу Джонсона (задача о двух станках).
При решении необходимо составить линейную диаграмму Ганта, схемы-графы обработки, записать алгоритм решения в виде таблицы состояний.
Дополнительно определить:
 - суммарное время простоя i - го станка, - суммарное время простоя i - го станка,
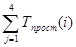 - суммарное время простоя j – й детали, - суммарное время простоя j – й детали,
 - суммарное время простоя 2 станков, - суммарное время простоя 2 станков,
 - суммарное время ожидания п=4 деталей. - суммарное время ожидания п=4 деталей.
Дополнительные условия и ограничения:
1 Маршрут обработки j - й детали в общем случае различен и задан жестко (в нашем случае маршруты одинаковы).
2 Длительность обработки j - й детали на j -
м станке в общем случае различна, время переналадки не учитывается.
3 Ограничения на сроки ожидания i - го станка и j - ой детали отсутствуют, приоритетов нет.
4 Ограничения на сроки выпуска j - ой детали отсутствуют, приоритетов нет.
5 Для каждой j - ой детали все операции, входящие в технологический маршрут должны быть выполнены и только один раз.
6 На каждом i - ом станке обрабатывается не более одной детали.
2.2 Решение задачи
По условию задачи мы имеем два станка, а маршруты обработки заданы жестко и вес одинаковы, а именно деталь сначала поступает на первый станок, затем на второй. Таким образом мы имеем задачу Джонсона (задача о двух станках). Обозначим:
Аj
- время обработки j - ой детали на 1 станке;
Вj
- время обработки j - ой детали на 2 станке.
Составим схемы-графы обработки
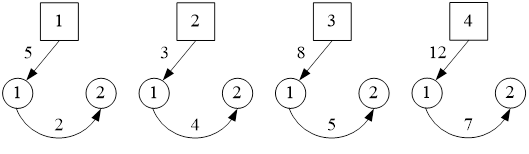
Рисунок 2.1 - Схема-граф обработки
Для определения последовательности обработки деталей просматриваем все значения A j и В j и находим любое из них минимальное. Если минимальное время получилось на первом станке, то такая деталь отправляется на обработку первой, если минимальное время получилось на втором станке, то такая деталь поступает на обработку последней. Строка, соответствующая рассмотренной детали, вычеркивается.
Таким образом, получили оптимальную в смысле критерия минимальной длительности обработки всей партии, последовательность обработки деталей.
Найдем последовательность обработки деталей на станках аналитическим способом. Для этого находим наименьшую по временным затратам стадию обработки детали на 1-ом станке.
Таблица 2.1 - Последовательность обработки деталей
| Деталь
|
А
|
В
|
| 1
|
5
|
2
|
| 2
|
3
|
4
|
| 3
|
8
|
5
|
| 4
|
12
|
7
|
Первой на обработку поступает вторая деталь, затем четвертая, после третья, а за ней первая деталь. Составим линейную диаграмму Ганта.
 Рисунок 2.2 - Линейная диаграмма Ганта Рисунок 2.2 - Линейная диаграмма Ганта
Матрица планов:

Матрицы времен начала каждой деталеоперации:
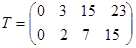
Суммарное время простоя каждого станка Тпр.ст
:
Тпр. 1ст.
= 0;
Тпр. 2ст.
= 4;
Суммарное время простоя всех станков:
Тпр. всех ст.
= 4.
Суммарное время ожидания для каждой детали Тож
:
Тож.1
= 21;
Тож2
= 4;
Тож3
= 8;
Тож4
= 0.
Суммарное время ожидания для всех деталей:
Тож.
= 33.
Суммарное время обработки всей партии деталей

Рассмотрим альтернативный вариант запуска деталей:
 Рисунок 2.3 - Альтернативная диаграмма Ганта Рисунок 2.3 - Альтернативная диаграмма Ганта
Матрица планов:
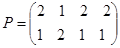
Матрицы времен начала каждой деталеоперации:
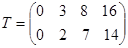
Суммарное время простоя каждого станка Тпр.ст
:
Тпр. 1ст.
= 0;
Тпр. 2ст.
= 0;
Суммарное время простоя всех станков:
Тпр. всех ст.
= 0.
Суммарное время ожидания для каждой детали Тож
:
Тож.1
= 1;
Тож2
= 10;
Тож3
= 1;
Тож4
= 2.
Суммарное время ожидания для всех деталей:
Тож.
= 14.
Суммарное время обработки всей партии деталей
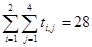
Таким образом, в результате решения данной задачи была найдена оптимальная последовательность обработки деталей (2, 4, 3, 1), по критерию минимального времени обработки всей партии деталей. При оптимальной последовательности обработки деталей, суммарное время обработки всей партии для данной задачи составит 28 единиц времени. Также была найдена альтернативная последовательность обработки деталей основанной на методе Джонсона, но с нулевым временем простоя станков и минимальным временем ожидания всех деталей.
3 Исследование технических объектов как систем массового обслуживания
Необходимо исследовать систему массового обслуживания (СМО) разомкнутого типа. Математическое ожидание числа требований, поступающих в систему в единицу времени составляет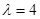 . .
Длительность обработки каждой поступившей партии сырья зависит только от его количества, следовательно, оно также является случайной величиной.
 , ,
где l
– среднее число требований, поступающих за единицу времени,
1/
m
–
среднее время обслуживания одним каналом одного требования.
Определим важнейшие характеристики работы СМО:
1. Вероятность того, что все обслуживающие каналы свободны:
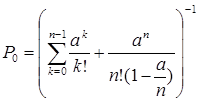 , где , где
n – число каналов обслуживания.
2. Среднее число занятых каналов:
 , где , где
М3 – среднее число свободных каналов, которое определяется по формуле:
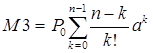 . .
3. Среднее число требований в системе:
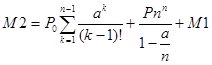 , ,
где М1 – средняя длина очереди.
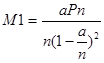 . .
4. Среднее время пребывания требований в очереди:
 , где , где
p - вероятность того, что все каналы заняты.
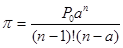 . .
Построим графики зависимостей характеристик работы СМО, определяемых приведенными выше формулами, от величины a
,
для системы с n=1 и n=2.
Вероятность простоя системы

Рисунок 4.1. – Вероятность простоя системы (n=2).
 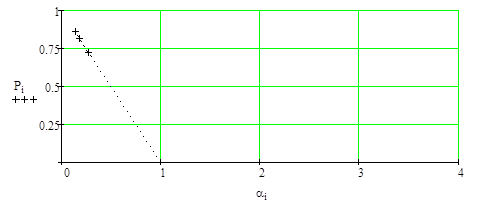
Рисунок 4.2. – Вероятность простоя системы (n=1).
Среднее число занятых каналов.
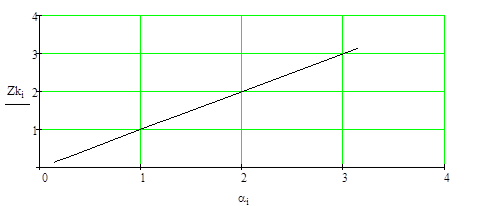
Рисунок 4.3. – Среднее число занятых каналов обслуживания (n=2).
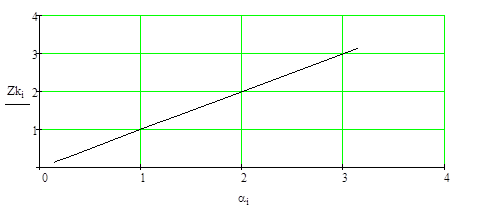
Рисунок 4.4. – Среднее число занятых каналов обслуживания (n=1).
Среднее число требований в системе.
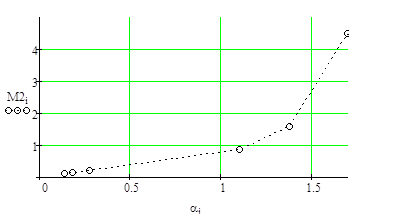
Рисунок 4.5. – Среднее число требований в системе (n=2).
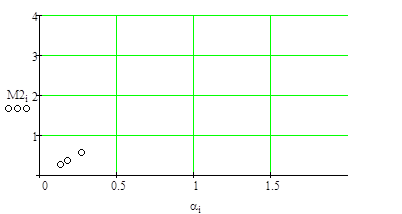
Рисунок 4.6. – Среднее число требований в системе (n=1).
Среднее время пребывания требований в очереди.
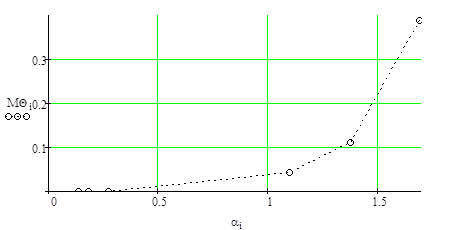
Рисунок 4.7. – Среднее время пребывания требований в очереди (n=2).
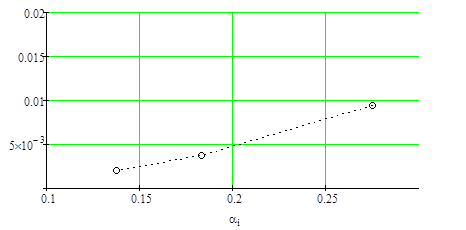
Рисунок 4.8. – Среднее время пребывания требований в очереди (n=1).
На следующем этапе решим задачу оптимальной загрузки системы, обеспечивающей минимизацию целевой функции:
 , ,
где С0
=20
– штраф за простой транспортных средств,
С1
=10 –
штраф за простой оборудования.
Для нахождения оптимальной загрузки системы построим график зависимости целевой функции от загрузки системы.
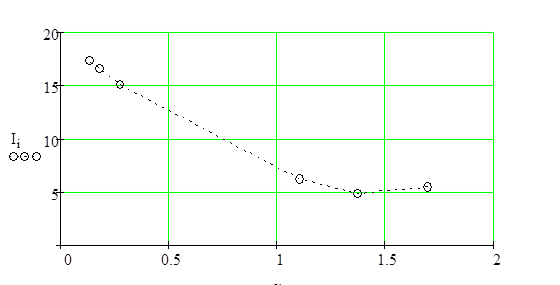
Рисунок 4.9. – Зависимости целевой функции от загрузки системы..
Из графика видно, что при средней длительности обработки каждой партии сырья а=1,375
целевая функция имеет минимальное значение, равное I
=4,824
.
Следовательно, оптимальная загрузка системы, обеспечивающая минимизацию целевой функции, при средней длительности обработки каждой партии сырья а=1,375.
Вывод: В данном разделе проводилось исследование систем массового обслуживания, в ходе которого были выявлены преимущества и недостатки применения одного и двух каналов обслуживания. Увеличение количества каналов в системе позволяет:
Снизить: вероятность занятости системы, среднюю длину очереди заявок, среднее число требований, находящихся в системе, вероятность занятости приборов, среднее время пребывания требования в очереди, среднее время пребывания требования в системе
Повысить: вероятность того, что в системе с ожиданием ни одно требование не будет находиться на обслуживании; число свободных от обслуживания приборов.
Однако, перечисленные выше пункты будут выполняться лишь в том случае, если интенсивность обслуживания µ будет одинакова для обоих случаев. В результате, вместе с перечисленными выше преимуществами появляется и ряд недостатков: снижается среднее число свободных от обслуживания приборов; повышается среднее время обслуживания заявки одним каналом.
Заключение
При выполнении курсового проекта была разработана АСУ ТП холодильной установки, включающая холодильную камеру и ресурсы, находящиеся в ней, составлена математическая модель объекта, построены статические характеристики объекта. Выбран и обоснован критерий оптимизации на основе одного из технико-экономических показателей, была построена двухуровневая система управления с координирующей подсистемой на верхнем уровне, формализовано представлен прямой алгоритм адаптации.
Была решена задача календарного планирования. Определена оптимальная последовательность обработки деталей, в смысле критерия оптимального времени обработки всей партии.
Был исследован технический объект как система массового обслуживания и найдена оптимальная загрузка системы в смысле заданного критерия.
|