| Различные стратегии построения кинетических моделей сложных реакций
Химическая кинетика – наука о скоростях химических реакций, о динамическом поведении реакционной системы на ее пути к химическому равновесию. Эта область физической химии тесно связана с учением о механизмах химических реакций, поскольку химическая кинетика – один из методов изучения механизмов, а механизм реакции, как теперь стало ясно, есть основа построения адекватной кинетической модели.
Закончился XX век – столетие триумфального развития химической кинетики, включающего как микроуровень элементарного акта, так и макроуровень многостадийных процессов, отличающихся феноменальной сложностью механизмов. Основы химической кинетики как науки были заложены в начале века работами нобелевских лауреатов Я.Вант-Гоффа (1901 г), С.Аррениуса (1903 г), В.Оствальда (1909 г), а также М.Боденштейна. Различные аспекты теории элементарного акта были развиты Г.Эйрингом, М.Поляни, В.Г.Левичем и Р.Р.Догонадзе, лауреатами нобелевской премии К.Фукуи и Р.Хоффманом (1981 г), Г.Таубе (1983 г), Р.Маркусом (1992 г) и многими другими исследователями. Теория цепных реакций создана работами М.Боденштейна, Й.Христиансена и нобелевских лауреатов Н.Н.Семенова и С.Н.Хиншельвуда (1956 г), их учеников и последователей.
Нобелевскими премиями были отмечены методы и результаты исследований быстрых элементарных реакций (М.Эйген, Дж.Портер, Р.Норриш, 1967 г), а также разработка методов исследования динамики элементарных актов газофазных реакций (Д.Хершбах, Я.Ли, Дж.Поляни, 1986 г).
Выдающиеся результаты были получены в области кинетики гомогенных и гетерогенных каталитических реакций. Отметим лишь теорию
кинетики гетерогенных реакций на неоднородных поверхностях (М.И.Темкин и С.З.Рогинский), теорию кинетики стационарных реакций Хориути-Темкина, открытие катализа комплексами палладия окислительных превращений олефинов (И.И.Моисеев, М.Н.Варгафтик, Я.К.Сыркин, Ю.Смидт и др.) и создание И.И.Моисеевым теории этих процессов на основе детальных кинетических исследований (премия им. А.П.Карпинского, 1999 г).
Двадцатое столетие увенчалось замечательным открытием новой области физической химии элементарного акта, названной "фемтохимия", и нобелевской премией по химии 1999 г американскому ученому, египтянину А.Зевейлу (A.Zewail) "за его исследования переходных состояний методом фемтосекундной (10–15
сек) лазерной спектроскопии". Достигнут предел измерения скоростей химических реакций. Появилась возможность следить за процессами, протекающими за время одного колебания атомов в химической связи – 10 – 100 фс. Переходное состояние ряда реакций фиксируется с разрешением 0.1 Å по координате реакции с полным спектральным портретом. Достигнут уровень разрешения соседних энергетических состояний ~10–4
см–1
.
Все результаты изучения "неравновесной" кинетики химических реакций на микроуровне чрезвычайно важны для обоснования базовых принципов химической кинетики, но пока мало полезны для решения задач макроуровня – исследования механизмов сложных реакций в газах, растворах и на поверхности твердого тела в условиях максвелл-больцмановского распределения, т.е. задач "равновесной" кинетики химических реакций. Если задача выяснения механизмов и построения кинетических моделей сложных реакций для "равновесной" кинетики газофазных радикально-цепных реакций решается практически (вследствие возможности построения максимальных механизмов или реакционных сетей с известными константами скорости элементарных стадий), то для сложных многомаршрутных процессов в растворах и на поверхности решение этой задачи только начинается. Эта проблема XXI века.
Существует три типа математических моделей (математического описания) сложных процессов. Стохастические
модели используют вероятностные представления о процессах в объекте исследования. Вычисляются функции распределения вероятностей для переменных параметров модели (концентрация, температура в случае химических процессов). Эти модели пока что редко используются в химической кинетике, но они оказались полезными для описания и моделирования поведения больших систем (химических комплексов, химических предприятий). Статистические
модели используют для описания эксперимента на работающем объекте исследования. Описывается связь значений входящих в систему и выходящих из системы переменных без использования физико-химической информации о происходящих в объекте процессах (модель черного ящика). Математическим описанием поведения системы обычно являются уравнения в форме полиномов. Для обеспечения статистической независимости параметров модели используют планирование эксперимента (например, ортогональные планы эксперимента). Детерминированные
модели основаны на закономерностях физико-химических процессов с определенной структурой модели. Именно такими моделями являются теоретически обоснованные кинетические модели. Детерминированным, структурным, теоретически обоснованным кинетическим моделям (КМ) химических процессов и будет посвящен данный курс лекций
.
При математическом моделировании каталитического процесса существует определенная иерархия математических моделей. Модели первого уровня – кинетические модели процессов на зерне твердого катализатора или в элементарном объеме жидкой фазы в гомогенной реакции, неосложненные процессами переноса массы, тепла и гидродинамическими факторами. Модели второго уровня в гетерогенном катализе рассматривают процессы в слое катализатора, а модели третьего уровня в гомогенном и гетерогенном катализе – это модели реактора в целом, включая все процессы переноса и структуру потоков. Модели первого уровня (КМ) будут рассматриваться в настоящем курсе лекций. Такие модели нужны для исследования новых реакций, для оптимизации каталитических процессов, расчетов промышленных реакторов (как составные части математической модели реактора), для создания систем автоматизированного управления процессом.
Итак, в основе построения КМ лежит механизм процесса, т.е. совокупность элементарных стадий, приводящая к превращению исходных реагентов в конечные продукты реакций, причем для одной и той же реакции (каталитической или некаталитической) существует некоторое конечное множество механизмов, определяемое существующим на сегодня объемом знаний и действующими в химии парадигмами.
Например, для реакции нуклеофильного замещения в ароматическом ядре ArX (некаталитической, катализируемой комплексами металлов или индуцированной переносом электронов с ArX и на ArX) установлено 8 механизмов:
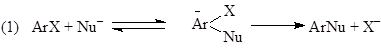
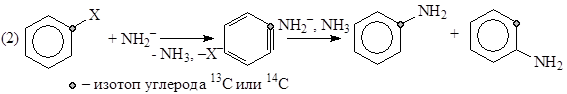
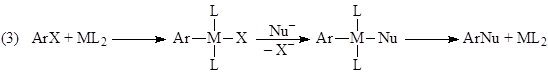
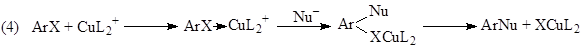

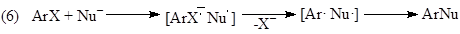
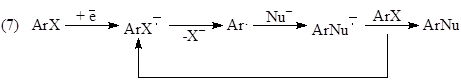
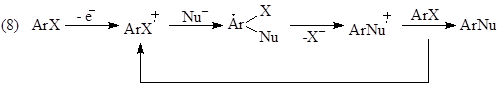
Предложено 13 одномаршрутных и 80 двухмаршрутных механизмов простой реакции гидрирования этилена на металлических катализаторах. Другими словами, для каждой реакционной системы (реагенты, катализатор) существует некоторое множество элементарных стадий – реакционная сеть (максимальный механизм), отдельные блоки которой реализуются в зависимости от природы катализатора, условий, заместителей в субстрате, степени окисления металла-катализатора.
В конце столетия наметилось объединение физико-химического и формально-кинетического подходов в изучении механизмов. Был сформулирован взгляд на механизм как на единство двух составляющих этого понятия – топологической (структурной) и химической составляющих
, и на их равноправие – нельзя однозначно установить структуру механизма (взаимосвязь элементарных стадий) на основе только формально-кинетического описания, так называемую "схему механизма", а потом наполнить ее химическим содержанием. Нельзя в общем случае из кинетических экспериментов получить информацию, необходимую для корректной идентификации схемы механизма, не задав этот механизм и не поставив соответствующие задачи для формально-кинетического метода.
Все эти обстоятельства вызвали необходимость пересмотра традиционной стратегии построения КМ.
Традиционная процедура построения КМ включает следующие этапы:
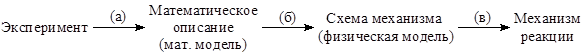
Главный недостаток этой процедуры (стратегии) – отсутствие алгоритмов однозначного выполнения всех этапов. Поскольку эксперимент может быть адекватно описан большим числом математических моделей (уравнений), исследователь должен иметь какую-либо гипотезу о схеме механизма (о структуре механизма) или о форме предполагаемых уравнений. При этом подбор возможных гипотез (иногда интуитивный) происходит уже после сделанного эксперимента. Нет алгоритма перехода от математической модели к физической модели (особенно для многомаршрутных реакций) (этап (б)). Переход к механизму реакции (этап (в)) также произволен и не формализован. На всех этапах этой стратегии присутствует естественное стремление получить хотя бы одно уравнение (и "схему механизма"), не противоречащее эксперименту, и, очень часто, ни о какой дискриминации набора гипотез не идет речи. Напротив, авторы такой схемы механизма начинают ставить эксперименты, чтобы доказать механизм, представляющийся автору наиболее разумным. Вместе с тем, уже давно установлено, что доказать какую-либо гипотезу нельзя. Можно доказательно отбросить неработающие гипотезы и показать согласие с экспериментом оставшихся гипотез – множества работающих гипотез
. Целесообразность выдвижения набора гипотез и получение множества работающих гипотез была убедительно обоснована более 100 лет назад американским ученым-геологом Т.Чемберленом.
Таким образом, рациональная стратегия построения КМ является четкой методологически обоснованной гипотетико-дедуктивной логической схемой исследования, поддержанной возможностями компьютеров и эффективным программным обеспечением. Суть этой стратегии отражена в последовательности ее этапов:
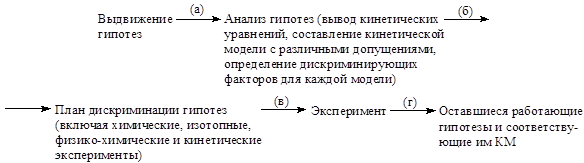
Дискриминация гипотез может включать дискриминацию стадий, блоков стадий, отдельных механизмов, узлов сопряжения в многомаршрутных реакциях.
Вид КМ (формы математического описания) зависит от особенностей механизма (линейный или нелинейный), условий проведения процесса (стационарный, квазистационарный, нестационарный), типа реактора (открытый, закрытый) и ряда принятых допущений. Линейным механизмом
называют механизм, элементарные стадии которого в прямом и обратном направлениях линейны по интермедиатам – только одно промежуточное соединение находится слева (или справа) от стрелки в элементарной стадии. Если в стадии участвует больше одного интермедиата (в том числе и 2 молекулы одного интермедиата), стадии нелинейны и механизм нелинейный
.
Самым общим видом КМ являются системы дифференциальных уравнений, алгебро-дифференциальных или алгебраических уравнений
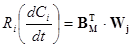 , (1) , (1)
правая часть которых всегда есть произведение матрицы стехиометрических коэффициентов для стадий механизма (транспонированной) на вектор-столбец скоростей элементарных стадий (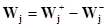 ). В случае линейных механизмов для реакции в стационарных или квазистационарных условиях правая часть уравнения (1) преобразуется в дробно-рациональные уравнения скоростей по реагентам (Ri
) или скоростей по маршрутам (Rp
). Системы алгебраических уравнений для нелинейных механизмов в общем случае не решаются, и уравнения типа (1) не приводятся к более простому дробно-рациональному виду. ). В случае линейных механизмов для реакции в стационарных или квазистационарных условиях правая часть уравнения (1) преобразуется в дробно-рациональные уравнения скоростей по реагентам (Ri
) или скоростей по маршрутам (Rp
). Системы алгебраических уравнений для нелинейных механизмов в общем случае не решаются, и уравнения типа (1) не приводятся к более простому дробно-рациональному виду.
В случае кинетики на неоднородных поверхностях в стационарных условиях скорость может описываться и степенным уравнением типа (2) (уравнение М.И.Темкина для синтеза аммиака):
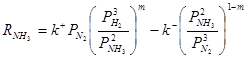 (2) (2)
Коэффициент m
= 0.5 в случае железного катализатора, k
+
/k
–
= K
– константа равновесия реакции
 . .
Особенности кинетических моделей для разных случаев, методы вывода кинетических уравнений и методы построения КМ в рамках рациональной стратегии будут рассмотрены в последующих разделах курса. Освоение традиционной стратегии – предмет домашнего задания (курсовой работы).
Вопросы для самоконтроля
1) Перечислить недостатки традиционной стратегии.
2) Методологическое обоснование рациональной стратегии.
3) Назвать основные этапы рациональной стратегии и перечислить преимущества этой стратегии на всех этапах построения КМ.
4) Назвать особенности КМ в случае линейных и нелинейных механизмов.
Литература для углубленного изучения темы
1. Шмид Р., Сапунов В.Н., Неформальная кинетика, М., Мир, 1985, 263 с (традиционная стратегия).
2. Брук Л.Г., Зейгарник А.В., Темкин О.Н., Вальдес-Перес Р., Методы выдвижения гипотез о механизмах реакций. Учебное пособие, М.: МИТХТ, 1999.
3. Темкин О.Н., Брук Л.Г., Зейгарник А.В., Некоторые аспекты стратегии изучения механизмов и построения кинетических моделей сложных реакций, Кинетика и катализ, 1993, т. 34, №3, с. 445 – 462.
4. Темкин О.Н., Проблемы кинетики сложных реакций, Росс. химический журнал, 2000, т. 44, №4, с. 58 – 65.
|