| Численные методы вычисления интегралов. Метод Ньютона-Котеса. Метод Гаусса
1. Численные методы вычисления интегралов. Постановка задачи
Решая физические задачи, часто приходится вычислять значения определённых интегралов от функций  . Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам. . Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам.
Прежде всего, рассмотрим случай, когда  - конечный интервал. - конечный интервал.
В таком случае, как известно, функция  является ограниченной, т.е. является ограниченной, т.е.  . В этом случае наиболее часто применяемый численный метод интегрирования состоит в том, что интеграл от . В этом случае наиболее часто применяемый численный метод интегрирования состоит в том, что интеграл от  заменяется некоторой линейной комбинацией значений заменяется некоторой линейной комбинацией значений  в в  точках точках  : :
 (1)
(1)
Формула (1) называется квадратурной формулой, а коэффициенты  - квадратурными коэффициентами или весами, абсциссы - квадратурными коэффициентами или весами, абсциссы  - узлами квадратурной формулы. - узлами квадратурной формулы.
Методы численного интегрирования классифицируются в зависимости от того, заданы ли значения аргумента через равные промежутки или нет. Так методы Ньютона-Котеса требуют, чтобы значения  были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов. были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.
2. Методы Ньютона-Котеса
Пусть  различные точки отрезка различные точки отрезка  , служащие узлами интерполяции для некоторой интерполирующей функцию , служащие узлами интерполяции для некоторой интерполирующей функцию  функции функции  . Тогда имеем: . Тогда имеем:
 (2)
(2)
где  - остаточный член. Предположим, что - остаточный член. Предположим, что
 (3)
(3)
причём  подобраны так, чтобы все интегралы подобраны так, чтобы все интегралы
 (4)
(4)
можно вычислить точно. Тогда мы получаем квадратурную формулу
 (5)
(5)
2.1 Формула трапеций
Частным случаем методов Ньютона-Котеса является квадратурная формула трапеции. Подынтегральную функцию будем интерполировать по формуле Лагранжа, в том случае, когда на каждом отрезке деления принимается линейная интерполяция, а результаты суммируются (рис 1):
Рис. 1.
а) графический вывод:
Определённый интеграл  , как известно, задаёт площадь , как известно, задаёт площадь  криволинейной трапеции криволинейной трапеции  , поэтому, вписав ломаную в дугу кривой , поэтому, вписав ломаную в дугу кривой  , мы получаем, что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций: , мы получаем, что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций:
 (6)
(6)
Между тем, очевидно, что
 (7)
(7)
Так как, в методах Ньютона-Котеса,  , учитывая (6) получаем: , учитывая (6) получаем:
 (8) (8)
или, соединяя подобные члены, имеем:
 (9) (9)
Формула (9) – называется формулой трапеций.
б) Аналитический вывод:
Выведем формулу трапеции аналитическим способом. Для этого используем интерполяционный многочлен Лагранжа для отрезка  , построим многочлен первой степени, который на концах отрезка принимает заданные значения , построим многочлен первой степени, который на концах отрезка принимает заданные значения  . Ясно, что в таком случае интерполирующая функция . Ясно, что в таком случае интерполирующая функция  имеет вид: имеет вид:
 (10) (10)
т.к. в методе Ньютона-Котеса  , учитывая (3) и (4), из (10) получаем: , учитывая (3) и (4), из (10) получаем:

 (11) (11)
Аналогично,  , т.е. , т.е.
 (12) (12)
Таким образом, получаем формулу:
 (13) (13)
тогда, используя свойство аддитивности оператора интегрирования, имеем:
 (14) (14)
где  . Получили формулу (14) трапеций, которая естественно, совпадает с (9). . Получили формулу (14) трапеций, которая естественно, совпадает с (9).
2.2 Формула Симпсона
Рассмотрим метод Ньютона-Котеса (т.е.  ), в случае интерполяции подинтегральной функции квадратичными функциями на каждом интервале деления. В данном случае мы имеем дело с параболическим интерполированием, поэтому на каждом интервале ), в случае интерполяции подинтегральной функции квадратичными функциями на каждом интервале деления. В данном случае мы имеем дело с параболическим интерполированием, поэтому на каждом интервале  , необходимо знание значения функции , необходимо знание значения функции  в трёх точках (т.к. в трёх точках (т.к.  имеет 3 неизвестных параметра – коэффициенты имеет 3 неизвестных параметра – коэффициенты  ). В качестве третьей точки на каждом отрезке ). В качестве третьей точки на каждом отрезке  - выбирается середина этого отрезка, т.е. точка - выбирается середина этого отрезка, т.е. точка  . .
Вывод формулы Симпсона будем производить аналитически. Как и в предыдущем случае применяем интерполяционный многочлен Лагранжа, для интерполирования функции  , на отрезке , на отрезке  , при чём считаем, что нам известны значения , при чём считаем, что нам известны значения  . Тогда, очевидно, что многочлен Лагранжа имеет вид квадратичной функции: . Тогда, очевидно, что многочлен Лагранжа имеет вид квадратичной функции:
 (15) (15)
Интегрируя (15) на отрезке  будем иметь формулу: будем иметь формулу:
 (16) (16)
используя свойство аддитивности интеграла, получаем:
 (17) (17)
где  является четным числом
( является четным числом
( - число делений отрезка - число делений отрезка  ,т.е. число равных отрезков разбиения). ,т.е. число равных отрезков разбиения).
Формула (17)-называется формулой Симпсона
.
Приняв обозначения  , получаем привычный вид квадратурных формул: , получаем привычный вид квадратурных формул:
а) Формула трапеций:
 (18) (18)
б) Формула парабол (Симпсона) (при  ) )
 (19) (19)
2.3 Метод Ромберга
Пусть промежуток интегрирования разбит на  равных частей и для этого разбиения по формуле трапеции получено значение равных частей и для этого разбиения по формуле трапеции получено значение  . Значение . Значение  - совпадает со значением вычисляемого интеграла, если интегрируемая функция - совпадает со значением вычисляемого интеграла, если интегрируемая функция  линейна, т.е. является многочленом первой степени. По формуле: линейна, т.е. является многочленом первой степени. По формуле:
 (20) (20)
называемой формулой Ромберга
, построим  - схему: - схему:
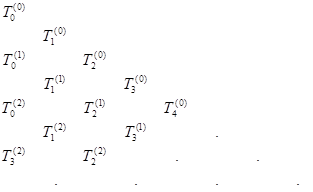 (21) (21)
Оказывается, что для интегрируемых по Риману функций, все столбцы и строки  - схемы сходятся к исходному значению интеграла. - схемы сходятся к исходному значению интеграла.
Пример
:
Выписать явные формулы для фрагмента  - схемы: - схемы:


 


Решение
:
Пусть  Тогда Тогда






3. Квадратурные формулы Гаусса
Во всех приведенных до сих пор формулах численного интегрирования Ньютона-Котеса и во всех формулах, получаемых методом Ромберга, используются равноотстоящие узлы. В случае квадратурных формул Гаусса это уже не так. Иначе говоря, смысл квадратурных формул Гаусса состоит в том, чтобы при наименьшем возможном числе узлов точно интегрировать многочлены наивысшей возможной степени. Можно показать, что при  гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени гауссовых узлах по полученной формуле можно точно интегрировать многочлены степени  . .
 (22) (22)
Для количества узлов и соответствующих значений  и и  - составлены таблицы, которые позволяют вычислять интегралы по формуле (22). - составлены таблицы, которые позволяют вычислять интегралы по формуле (22).
Для понимания сути этих таблиц рассмотрим пример.
Пример:
Пусть нам нужно составить квадратурную формулу с двумя узлами  ,по которой точно интегрируются многочлены до ,по которой точно интегрируются многочлены до  степень включительно. степень включительно.
Решение:
Искомая формула имеет вид:
 ,(23)
,(23)
где  - остаток, который обращается в нуль, для - остаток, который обращается в нуль, для
 , при , при  . .
Тогда, подставляя в (23) имеем:
 (24) (24)
Отсюда, приравнивая коэффициенты при   , справа и слева, получаем систему уравнений: , справа и слева, получаем систему уравнений:
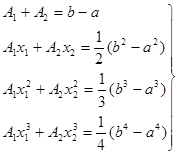 (25) (25)
Ее решение имеет вид:
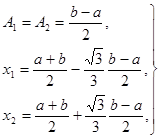 (26) (26)
Следовательно, искомая квадратурная формула такова
:
 .(27) .(27)
Ясно, что если нам нужно вычислить интеграл со многими узловыми точками, действуем следующим образом:
а) промежуток интегрирования  делим на делим на  - равных промежутков и на каждом маленьком промежутке - равных промежутков и на каждом маленьком промежутке  применяем формулу Гаусса с неравноотстоящими узлами (27); применяем формулу Гаусса с неравноотстоящими узлами (27);
б) полученные результаты складываем.
В случае, когда  , оказывается, что узловыми точками при делении отрезка на , оказывается, что узловыми точками при делении отрезка на  - частей являются корни соответствующих многочленов Лежандра. - частей являются корни соответствующих многочленов Лежандра.
Для вычисления кратных интегралов, их сводят обычно к повторным интегралам, а далее применяют те же самые кубатурные формулы для каждого значения узловых точек, что и в одномерном случае. Однако, надо иметь в виду, что кратные интегралы значительно сложнее вычислять с заданной точностью.
Точность произведённых вычислений зависит от точности аппроксимации подынтегральной функции многочленами.
4. Оценка интегралов
При численном интегрировании наряду с приближёнными формулами представляет также интерес нахождение нижних и верхних границ интегралов. Рассмотрим два метода оценки интегралов:
а) оценка интеграла в случае, когда подинтегральная функция  , удовлетворяет условию: , удовлетворяет условию:
 для для  (28) (28)
б) общий случай.
Рассмотрим интеграл:
 (29) (29)
где  , ,  . Не умоляя общность, будем считать, что . Не умоляя общность, будем считать, что  , ,  , тогда (Рис. 1) ясно, что , тогда (Рис. 1) ясно, что
         
К Е
N
М
0    
Рис. 1
0    
Площадь криволинейной трапеции  заключена между площадями aMNb и aKEb, т.е. заключена между площадями aMNb и aKEb, т.е.
 (30) (30)
Очевидно, что
 (31) (31)
 (32) (32)
Таким образом, для оценки интеграла в случае  , имеем: , имеем:
 (33) (33)
если же  , неравенство (33) заменяется на обратное. , неравенство (33) заменяется на обратное.
б) Другой принцип грубой, но зато общей оценки значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями  и и  , т.е. , т.е.
 , ,  (34) (34)
Тогда
 (35) (35)
5. Вычисление интегралов методом Монте-Карло
Пусть нам нужно вычислить интеграл:
 (36) (36)
В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным методам случайного поиска. К таким методам относится метод Монте-Карло.
Для вычисления интеграла (36) методом Монте-Карло, заменим переменную интегрирования  таким образом, чтобы пределы интегрирования таким образом, чтобы пределы интегрирования  отобразились соответственно в отобразились соответственно в  . Для этого нужно воспользоваться преобразованием: . Для этого нужно воспользоваться преобразованием:
 (37) (37)
тогда интеграл (36) принимает вид:
 (38) (38)
Для вычисления же интеграла на  имеем формулу: имеем формулу:
 (39) (39)
где  - случайные числа, равномерно распределённые на - случайные числа, равномерно распределённые на  . Таким образом, по методу Монте-Карло, интеграл (36) считается по формуле: . Таким образом, по методу Монте-Карло, интеграл (36) считается по формуле:
 (40) (40)
где  - равномерно распределённые случайные числа из промежутка - равномерно распределённые случайные числа из промежутка  . .
Аналогично, для кратных интегралов. Получаем:
 (41) (41)
где  - случайные точки, равномерно распределённые на квадрате - случайные точки, равномерно распределённые на квадрате  (Здесь знак « (Здесь знак « » означает декартовое произведение). » означает декартовое произведение).
В случае, когда область интегрирования является сложным множеством  (рис. 6), пользуемся прямоугольником (рис. 6), пользуемся прямоугольником  , который описывается вокруг множества , который описывается вокруг множества  . И интеграл по множеству . И интеграл по множеству  заменяем интегралом по прямоугольнику заменяем интегралом по прямоугольнику  , который уже умеем вычислять по формуле (41). Замена интеграла по множеству , который уже умеем вычислять по формуле (41). Замена интеграла по множеству  производится соотношением: производится соотношением:
 (42) (42)
где
 (43) (43)
таким образом:
 (44) (44)
который легко рассчитывается по формуле (41).
Аналогично вычисляются и трёхкратные интегралы. Этот подход легко обобщается для n-кратных интегралов.
Литература
1. Р.В. Хемминг. Численные методы, Наука, М.,1998
2. Коллатц., Ю.Альбрехт. Задачи по прикладной математике. Мир, М.,1998.
3. Т.Шуп. Решение инженерных задач на ЭВМ. Мир, М., 1992.
4. К.Бреббия, Ж. Теллес, Л. Врубел.Методы граничных элементов. Мир, М.,1987.
5. И.С.Берехин., Н.П.Жидков. Методы вычислений, ч.1., М.,1982.
|