| Приложения определенного интеграла к решению некоторых задач механики и физики
1. Моменты и центры масс плоских кривых.
Если дуга кривой задана уравнением y
=
f
(
x
),
a
≤
x
≤
b
, и имеет плотность 1
)  =
(
x
)
, то статические моменты этой дуги Mx
и My
относительно координатных осей Ox
и O
y равны
моменты инерции I
Х
и I
у
относительно тех же осей Ох
и Оу
вычисляются по формулам
а координаты центра масс  и  — по формулам
где l
— масса дуги, т. е.
Пример 1.
Найти статические моменты и моменты инерции относительно осей Ох
и Оу
дуги цепной линии y
=
chx
при 0≤
x
≤
1.
1
) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и =1.
◄ Имеем:  Следовательно,
 ►
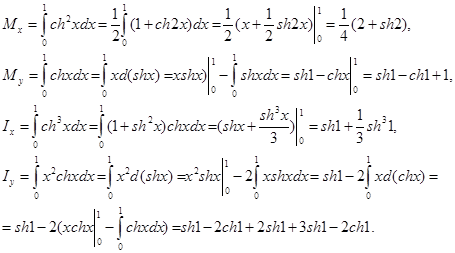Пример 2.
Найти координаты центра масс дуги окружности x=acost, y=asint,
расположенной в первой четверти.
◄ Имеем: 
Отсюда получаем:
►
В приложениях часто оказывается полезной следующая
Теорема Гульдена
. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
Пример 3.
Найти координаты центра масс полуокружности 
◄Вследствие симметрии  . При вращении полуокружности вокруг оси Ох
получается сфера, площадь поверхности которой равна  , а длина полуокружности равна па. По теореме Гульдена имеем 
Отсюда  , т.е. центр масс C
имеет координаты C
 .
2. Физические задачи.
Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.
Пример 4.
Скорость прямолинейного движения тела выражается формулой  (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
◄ Так как путь, пройденный телом со скоростью  (t
) за отрезок времени [t1
,t2
], выражается интегралом
то имеем:
 ►
Пример 5.
Какую работу необходимо затратить для того, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту /i? Чему равна работа, если тело удаляется в бесконечность?
<4| Работа переменной силы / (#), действующей вдоль оси Ох на отрезке [а, Ь], выражается интегралом
|
