| СОДЕРЖАНИЕ
Введение
§1. Понятие энтропии. Энтропия как мера степени неопределенности
§2. Понятие об информации. Измерение информации
§3. Теорема Шеннона о кодировании при наличии помех
§4. Пример использования энтропии в прогнозировании и ее значение для прогнозирования. Применение к рискам
Заключение
Список использованной литературы
Введение
Предметом работы является энтропия и информация. Целью данной работы является изучение энтропии, информации и применения данных понятий к рискам. Поставленная цель ставит решение следующих задач: рассмотрения понятия энтропии, статистического смысла данного понятия, энтропии как меры степени неопределенности, понятия об информации, теоремы Шеннона о кодировании при наличии помех, использования энтропии в прогнозировании и применения энтропии к рискам.
Данная тема актуальна, так как трудно найти понятия более общие для всех наук (не только естественных) и, вместе с тем, иногда носящих оттенок загадочности, чем энтропия и информация. Отчасти это связано с самими названиями. Если бы не звучное название “энтропия” осталась бы с момента первого рождения всего лишь “интегралом Клаузиуса”, вряд ли она бы не рождалась вновь и вновь в разных областях науки под одним именем. Кроме того, ее первооткрыватель Клаузиузус, первым же положил начало применению введенного им для, казалось бы узкоспециальных термодинамических целей понятия к глобальным космологическим проблемам (тепловая смерть Вселенной). С тех пор энтропия многократно фигурировала в оставшихся навсегда знаменитыми спорах. В настоящее время универсальный характер этого понятия общепризнан и она плодотворно используется во многих областях.
Термин “информация” замечателен тем, что, существующему с давних пор бытовому понятию, К.Шенноном был придан математически точный смысл. Неопределенно-бытовой смысл этого термина уже научного. Это приводило и приводит ко многим недоразумениям/ Данную тему опишем с помощью следующих методов: синтеза, анализа, индукции, дедукции, сравнения и расчетного метода.
Работа изложена на 26 страниц и состоит из четырех параграфов. В работе 1 таблица и 7 примеров.
§1. Понятие энтропии. Статистический смысл понятия энтропии. Энтропия как мера степени неопределенности
Энтропия (от греч. entropia - поворот, превращение) - мера неупорядоченности больших систем. Впервые понятие "энтропия" введено в XIX в. в результате анализа работы тепловых машин, где энтропия характеризует ту часть энергии, которая рассеивается в пространстве, не совершая полезной работы (отсюда определение: энтропия - мера обесценивания энергии). Затем было установлено, что энтропия характеризует вероятность определенного состояния любой физической системы среди множества возможных ее состояний. В закрытых физических системах все самопроизвольные процессы направлены к достижению более вероятных состояний, т. е. к максимуму энтропии . В равновесном состоянии, когда этот максимум достигается, никакие направленные процессы невозможны. Отсюда возникла гипотеза о тепловой смерти Вселенной. Однако распространение на всю Вселенную законов, установленных для закрытых систем, не имеет убедительных научных оснований. В XX в. понятие " энтропия " оказалось плодотворным для исследования биосистем, а также процессов передачи и обработки информации. Эволюция в целом и развитие каждого организма происходит благодаря тому, что биосистемы, будучи открытыми, питаются энергией из окружающего мира. Но при этом биопроцессы протекают таким образом, что связанные с ними "производство энтропии " минимально. Это служит важным руководящим принципом и при разработке современных технологических процессов, при проектировании технических систем. Количественная мера информации формально совпадает с "отрицательно определенной " энтропией. Но глубокое понимание соответствия энтропии физической и информационной остается одной из кардинальных недостаточно исследованных проблем современной науки. Ее решение послужит одним из важных факторов становления нового научно-технического мышления.
Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Эти трактовки имеют глубокую внутреннюю связь. Например, на основе представлений об информационной энтропии можно вывести все важнейшие положения статистической физики.
Теория информации возникла для описания передачи и приёма сообщений в процессе деятельности человека. Во всех её задачах присутствуют понятия передатчика и приёмника, сигнала-сообщения, событий и их вероятностей. Существование цели передачи информации в теории информации выражается тем, что вводится понятие известного заданного события. Для него может быть определена вероятность р0
наступления до приёма сообщения и р1
после приёма.
В силу определения информации как устранённой неопределённости в достижении цели строгая (то есть математическая) формализация понятия об информации требует выразить математическим соотношением, что есть неопределённость в достижении цели.
Существование неопределённости связано с участием вероятностей в осуществлении событий. Устранение неопределённости есть увеличение вероятности наступления того, что задано как цель. Поэтому вероятности должны участвовать в математической формулировке величины устранённой неопределённости.
Первая удачная попытка реализовать определение информации на такой основе осуществлена в 1928 г. Л. Хартли. Пусть возможно в данных условиях n вариантов некоторого результата. Целью является один из них. Хартли предложил характеризовать неопределённость логарифмом числа n. То есть log n является количественной мерой неопределённости. Выбор основания логарифма связан с понятием об алфавитах для описания информации. Этот выбор существенен для экономичности кодирования в технических устройствах или живых системах (сокращения потоков импульсов или аналоговых сигналов), но не меняет самого количества информации как устранённой неопределённости за счёт того, что перед логарифмом вводится безразмерный множитель, выражаемый модулем перехода между основаниями логарифмов. От него зависят названия единиц информации.
При математическом описании неопределённости (например способом Хартли) в случае равновероятных результатов можно перейти от их числа n
к обратной величине - вероятности р
одного из них. В терминах связи конкретно говорят о вероятности переданного сообщения р0
у приёмника до приёма сообщения. Устранение неопределённости выражается тем, что вероятность переданного сообщения у приёмника после приёма сигнала возрастает и становится р1
. Тогда количественная мера s
полученной информации (устранённой неопределённости) выражается логарифмом отношения вероятностей:

Оно равноправно по отношению к любому конкретному сообщению и имеет разную величину в зависимости от величин р0
и р1
для него. В частном случае, когда при передаче полностью отсутствую шумы и сбои, искажающие сигнал, вероятность р0
равна единице.
Недостаток этого определения в том, что оно справедливо в приближении равновероятности всех исходов. Это выполняется далеко не всегда. В пределе в этом определении невероятному исходу приравнивается неизбежный. В 1948 г. это исправил К. Шеннон, который определил в качестве меры неопределённости выражение:

где

есть вероятности отдельных исходов. Он предложил называть эту величину "энтропией", не поясняя связей и различий этого термина с общеизвестой энтропией в физике. Знак минус в предыдущей формуле отражает тот факт, что вероятности всегда меньше единицы, а энтропия знакопостоянная функция, для которой привычно задан положительный знак. Определение Шеннона сокращённо зависывают в виде:
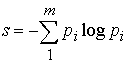 , ,
подразумевая как очевидное, что признаки (аргументы), по отношению к которым определены события и их вероятности, могут быть существенно разными, а в эта формула (суммирование в ней) справедлива только для однородных признаков.
§2. Понятие об информации. Измерение информации
Понятие информации (informatio - разъяснение, осведомление, изложение) является одним из основных, ключевых понятий не только в информатике (в информологии - области знаний, изучающей проявление информации, её представление, измерение и т.д.), но и в математике, в физике и др. Понятие “информация” - плохо формализуемое и структурируемое понятие. В силу его всеобщности, объёмности, расплывчатости оно часто понимается неточно и неполно не только обучаемыми. Как правило, это понятие в курсе информатики не определяется, принимается как исходное базовое понятие, неопределяемый терм.
Информация трактуется по разному, например, как:
• любая сущность, которая вызывает изменения в некоторой информационно-логической (инфологической - состоящей из данных, знаний, абстракций и т.д.) модели системы (математика, системный анализ);
• сообщения, полученные системой от внешнего мира в процессе адаптивного управления, приспособления (теория управления, кибернетика);
• отрицание энтропии, отражение меры хаоса в системе (термодинамика);
• связи, устраняющие неопределённость в системе (теория информации);
• вероятность выбора в системе (теория вероятностей);
• отражение разнообразия в системе (физиология, биокибернетика);
• отражение материи, атрибут сознания, “интеллекта” системы (философия).
Но существует более полное понятие. Информация - это некоторая последовательность (налицо упорядоченность) сведений, знаний, которые актуализируемы (получаемы, передаваемы, преобразуемы, сжимаемы или регистрируемы) с помощью некоторых знаков (символьного, образного, жестового, звукового, сенсомоторного типа). Это приращение, развитие, актуализация знаний, возникающее в процессе целеполагающей интеллектуальной деятельности человека. Никакая информация, никакое знание не появляется сразу - этому предшествует этап накопления, осмысления, систематизации опытных данных, взглядов. Знание - продукт такого процесса. Мышление - необходимый атрибут такого процесса.
Информация может существовать в пассивной (не актуализированной) и активной (актуализированной) форме.
Пример. Информация актуализируется сообщениями, при этом формы облачения информации в сообщения различны, например, для живых существ - сигналы, жесты, для технических устройств - сигналы. Информация передаваемая от одного человека другому, может передаваться символами (письмо), жестами (сигнальщик на боевом корабле), звуками (диктор), геометрическими фигурами (чертёжник), художественными образами (балерина). Информация передающаяся животными может быть передана звуками (лай, вой, писк), ситуационным поведением (образами). Информация в технических устройствах, автоматах может быть передана электрическими, магнитными, световыми импульсами, как это происходит в ЭВМ.
Информация в философском аспекте бывает, в основном: мировоззренческая; эстетическая; религиозная; научная; бытовая; техническая; экономическая; технологическая.
Все это (с человеком) составляет ноосферу общества - более высокое состояние биосферы, возникшее в результате эволюции, структурирования, упорядочивания и гармонизации связей в природе и обществе под воздействием целеполагающей деятельности человечества. Это понятие введено впервые В. И. Вернадским в качестве отражения эволюции общества и природы т.е. системы, в рамках которой потенциально может быть реализовано гармоническое, устойчивое развитие (эволюция) систем “Общество” и “Природа”, а также постепенное слияние, интеграция и гармонизация наук о природе, познании и об обществе. Без этого невозможно построение информационного общества.
Информация может оказаться и вредной, влияющей негативно на сознание, например, воспитывающей восприятие мира от безразличного или же некритического - до негативного, "обозлённого", неадекватного. Информационный поток - достаточно сильный раздражитель.
Пример. Негативной информацией - раздражителем может быть информация о крахе коммерческого банка, о резком росте (спаде) валютного курса, об изменении налоговой политики и др.
Информация не существует без других типов ресурсов - энергии, вещества, организации, как и они не могут существовать без информации. Любые взаимодействия систем (подсистем) - взаимодействия всегда материальноэнерго-информационные. Выявление (структурирование, упорядочивание, установление отношений), формализация (описание формальными средствами, языками), изучение (разработка моделей, методов, алгоритмов), применение (разработка и актуализация технологий) этих взаимодействий и составляет основную задачу информатики - как науки, как человеческой деятельности.
Если отвлечься от конкретного смыслового содержания информации и рассматривать сообщения информации как последовательности знаков, сигналов, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Информация может пониматься и интерпретироваться по разному. Вследствие этого имеются различные подходы к определению методов измерения информации, меры количества информации. Раздел информатики (теории информации) изучающий методы измерения информации называется информметрией.
Количество информации - числовая величина, адекватно характеризующая актуализируемую информацию по разнообразию, сложности, структурированности, определённости, выбору (вероятности) состояний отображаемой системы.
Если рассматривается система, которая может принимать одно из n
возможных состояний, то актуальна задача оценки такого выбора, исхода. Такой оценкой может стать мера информации (или события). Мера - это некоторая непрерывная действительная неотрицательная функция, определённая на множестве событий и являющаяся аддитивной т.е. мера конечного объединения событий (множеств) равна сумме мер каждого события.
1. Мера Р. Хартли
. Пусть имеется N состояний системы S или N опытов с различными, равновозможными последовательными состояниями системы. Если каждое состояние системы закодировать, например, двоичными кодами определённой длины d, то эту длину необходимо выбрать так, чтобы число всех различных комбинаций было бы не меньше, чем N. Наименьшее число, при котором это возможно или мера разнообразия множества состояний системы задаётся формулой Р. Хартли: H=k log а
N, где k - коэффициент пропорциональности (масштабирования, в зависимости от выбранной единицы измерения меры), а - основание системы меры.
Если измерение ведётся в экспоненциальной системе, то k=1, H=lnN (нат); если измерение - в двоичной системе, то k=1/ln2, H=log2
N (бит); если измерение - в десятичной системе, то k=1/ln10, H=lgN (дит).
Пример. Чтобы узнать положение точки в системе из двух клеток т.е. получить некоторую информацию, необходимо задать 1 вопрос ("Левая или правая клетка?"). Узнав положение точки, мы увеличиваем суммарную информацию о системе на 1 бит (I=log2
2). Для системы из четырех клеток необходимо задать 2 аналогичных вопроса, а информация равна 2 битам (I=log2
4). Если система имеет n различных состояний, то максимальное количество информации равно I=log2
n.
По Хартли, для того, чтобы мера информации имела практическую ценность - она должна быть такова, чтобы отражала количество информации пропорционально числу выборов.
Пример. Имеются 192 монеты из которых одна фальшивая. Определим сколько взвешиваний нужно произвести, чтобы определить ее. Если положить на весы равное количество монет, то получим 2 возможности (мы сейчас отвлекаемся от того, что в случае фальшивой монеты таких состояний будет два - состояния независимы): а) левая чашка ниже; б) правая чашка ниже. Таким образом, каждое взвешивание дает количество информации I=log2
2=1 и, следовательно, для определения фальшивой монеты нужно сделать не менее k взвешиваний, где k удовлетворяет условию log2
2k³ log2
192. Отсюда, k=7. Следовательно, нам необходимо сделать не менее 7 взвешиваний (достаточно семи).
Формула Хартли отвлечена от семантических и качественных, индивидуальных свойств рассматриваемой системы (качества информации, содержащейся в системе, в проявлениях системы с помощью рассматриваемых N состояний системы). Это основная положительная сторона этой формулы. Но имеется и основная отрицательная сторона: формула не учитывает различимость и различность рассматриваемых N состояний системы.
Уменьшение (увеличение) Н может свидетельствовать об уменьшении (увеличении) разнообразия состояний N системы.
Обратное, как это следует из формулы Хартли (основание логарифма берётся больше 1), - также верно.
2.Мера К. Шеннона.
Формула Шеннона дает оценку информации независимо, отвлеченно от ее смысла:
n I = — å pi
log2
pi , i=1
где n - число состояний системы; рi
- вероятность (или относительная частота) перехода системы в i-ое состояние, причем сумма всех pi
равна 1.
Если все состояния равновероятны (т.е. рi
=1 /n), то I=log2
n.
К. Шенноном доказана теорема о единственности меры количества информации. Для случая равномерного закона распределения плотности вероятности мера Шеннона совпадает с мерой Хартли. Справедливость и достаточная универсальность формул Хартли и Шеннона подтверждается и данными нейропсихологии.
Пример. Время t реакции испытуемого на выбор предмета из имеющихся N предметов линейно зависит от log2
N: t=200+180log2
N (мс). По аналогичному закону изменяется и время передачи информации в живом организме. В частности, один из опытов по определению психофизиологических реакций человека состоял в том, что перед испытуемым большое количество раз зажигалась одна из n лампочек, которую он должен указать. Оказалось, что среднее время, необходимое для правильного ответа испытуемого, пропорционально не числу n лампочек, а именно величине I определяемой по формуле Шеннона, где pi
- вероятность зажечь лампочку номер i.
Сообщение о наступлении события с меньшей вероятностью несёт в себе больше информации, чем сообщение о наступлении события с большей вероятностью. Сообщение о наступлении достоверно наступающего события несёт в себе нулевую информацию (и это вполне ясно, - событие всё равно произойдёт когда-либо).
Если в формуле Шеннона обозначить fi
= —n log2
pi , то получим, что I можно понимать как среднеарифметическое величин fi
.
Отсюда, fi
можно интерпретировать как информационное содержание символа алфавита с индексом i и величиной pi
вероятности появления этого символа в сообщении, передающем информацию.
Основными положительными сторонами формулы Шеннона является её отвлечённость от семантических и качественных, индивидуальных свойств системы, а также то, что в отличие от формулы Хартли она учитывает различность, разновероятность состояний - формула имеет статистический характер (учитывает структуру сообщений), делающий эту формулу удобной для практических вычислений. Основные отрицательные стороны формулы Шеннона: она не различает состояния (с одинаковой вероятностью достижения, например), не может оценивать состояния сложных и открытых систем и применима лишь для замкнутых систем, отвлекаясь от смысла информации.
Увеличение (уменьшение) меры Шеннона свидетельствует об уменьшении (увеличении) энтропии (организованности) системы. При этом энтропия может являться мерой дезорганизации систем от полного хаоса (S=Smax) и полной информационной неопределённости (I=Imin) до полного порядка (S=Smin) и полной информационной определённости (I=Imax) в системе.
Пример. Чем ближе движущийся объект к нам, тем полнее информация обрабатываемая нашими органами чувств, тем чётче и более структурирован (упорядочен) объект. Чем больше информации мы имеем о компьютерной технике, тем меньше психологический барьер перед ним (согласно основному соотношению между энтропией и информацией).
3. Термодинамическая мера.
Информационно-термодинамический подход связывает величину энтропии системы с недостатком информации о её внутренней структуре (не восполняемым принципиально, а не нерегистрируемым). При этом число состояний определяет, по существу, степень неполноты наших сведений о системе.
Пусть дана термодинамическая система (процесс) S, а Н0
, Н1
- термодинамические энтропии системы S в начальном (равновесном) и конечном состояниях термодинамического процесса, соответственно. Тогда термодинамическая мера информации (негэнтропия) определяется формулой:
Н(Н0
,Н1
)=Н0
— Н1
.
Эта формула универсальна для любых термодинамических систем. Уменьшение Н(Н0
,Н1
) свидетельствует о приближении термодинамической системы S к состоянии статического равновесия (при данных доступных ей ресурсах), а увеличение - об удалении.
Поставим некоторый вопрос о состоянии некоторой термодинамической системы. Пусть до начала процесса можно дать p1
равновероятных ответов на этот вопрос (ни один из которых не является предпочтительным другому), а после окончания процесса - p2
ответов. Изменение информации при этом:
D I
= k ln(p1
/ p2
) = k (ln p1
— ln p2
).
Если p1
> p2
(D I
>0) - прирост информации, т.е. сведения о системе стали более определёнными, а при p10 - более низкой организации).
Термодинамическая мера (энтропия) применима к системам, находящимся в тепловом равновесии. Для систем, далёких от теплового равновесия, например, живых биосистем, мера - энтропия - менее подходящая.
4. Энергоинформационная (квантово-механическая) мера.
Энергия (ресурс) и информация (структура) - две фундаментальные характеристики систем реального мира, связывающие их вещественные, пространственные, временные характеристики. Сейчас актуально говорить о биоэнергоинформационных мерах, отражающих механизм взаимосвязей биофизикоинформационных и вещественно-энергетических процессов в системе, в ноосфере.
3. Теорема Шеннона о кодировании при наличии помех
Рассмотрим первую теорему Шеннона. Первая теорема Шеннона о передаче информации, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом: п
ри отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.
Используя понятие избыточности кода, можно дать более короткую формулировку теоремы: при отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
Данные утверждения являются теоремами и, следовательно, должны доказываться, однако доказательства мы опустим. Для нас важно, что теорема открывает принципиальную возможность оптимального кодирования. Однако необходимо сознавать, что из самой теоремы никоим образом не следует, как такое кодирование осуществить практически – для этого должны привлекаться какие-то дополнительные соображения, что и станет предметом нашего последующего обсуждения.
Далее в основном ограничим себя ситуацией, когда M = 2, т.е. для представления кодов в линии связи используется лишь два типа сигналов – с практической точки зрения это наиболее просто реализуемый вариант (например, существование напряжения в проводе (будем называть это импульсом) или его отсутствие (пауза); наличие или отсутствие отверстия на перфокарте или намагниченной области на дискете); подобное кодирование называется двоичным. Знаки двоичного алфавита принято обозначать "0" и "1", но нужно воспринимать их как буквы, а не цифры. Удобство двоичных кодов и в том, что при равных длительностях и вероятностях каждый элементарный сигнал (0 или 1) несет в себе 1 бит информации (log2
M = 1); тогда из (1), теоремы Шеннона:
I1(A) K(2) K(2)
и первая теорема Шеннона получает следующую интерпретацию: при отсутствии помех передачи средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
Применение формулы (2) для двоичного кодирования дает:
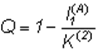
Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей). При этом возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов. Приемное устройство фиксирует интенсивность и длительность сигналов. Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности. Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код). Наконец, коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов). В результате при кодировании (алфавитном и словесном) возможны следующие варианты сочетаний:
Таблица 1.
| Варианты сочетаний длительности элементарных сигналов
|
Кодировка первичных символов (слов)
|
Ситуация
|
| одинаковые
|
равномерная
|
(1)
|
| одинаковые
|
неравномерная
|
(2)
|
| разные
|
равномерная
|
(3)
|
| разные
|
неравномерная
|
(4)
|
В случае использования неравномерного кодирования или сигналов разной длительности (ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).
Длительность двоичного элементарного импульса ( ) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время ) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время 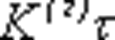 . Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей. . Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
§4. Пример использования энтропии в прогнозировании и ее значение для прогнозирования. Применение к рискам
Прогнозирование — частный вид моделирования как основы познания и управления.
Роль прогнозирования в управлении страной, отраслью, регионом, предприятием очевидна. Необходимы учет СТЗП-факторов (социальных, технологических, экономических, политических), факторов конкурентного окружения и научно-технического прогресса, а также прогнозирование расходов и доходов предприятий и общества в целом (в соответствии с жизненным циклом продукции — во времени и по 11-ти стадиям международного стандарта ИСО 9004). Проблемы внедрения и практического использования математических методов эконометрического прогнозирования связаны прежде всего с отсутствием в нашей стране достаточно обширного опыта подобных исследований, поскольку в течение десятилетий планированию отдавался приоритет перед прогнозированием.
В конкретных задачах прогнозирования необходимо провести классификацию рисков, поставить задачу оценивания конкретного риска, провести структуризацию риска. Риски необходимо учитывать при прогнозировании экономических последствий принимаемых решений, поведения потребителей и конкурентного окружения, внешнеэкономических условий и макроэкономического развития России, экологического состояния окружающей среды, безопасности технологий, экологической опасности промышленных и иных объектов.
Большое число рисков связано с природными явлениями. Их можно объединить под именем «экологические». К ним относятся, в частности риски, связанные с неопределенностью ряда природных явлений. Типичным примером является погода, от которой зависят урожайность (а потому и цены на сельскохозяйственные товары), расходы на отопление и уборку улиц, доходы от туризма и др. Особое значение имеют риски, связанные с недостаточными знаниями о природе (например, неизвестен точный объем полезных ископаемых в том или ином месторождении, а потому нельзя точно предсказать развитие добывающей промышленности и объем налоговых поступлений от ее предприятий). Нельзя забывать о рисках экологических бедствий; и катастроф типа ураганов, смерчей, землетрясений, цунами, селей и др.
В настоящее время при компьютерном и математическом моделировании для описания неопределенностей все чаще используют такой метод, как энтропия. Некоторые виды неопределенностей связаны с безразличными к организации силами — природными (погодные условия) или общественными (смена правительства).
Разнообразные формальные методы оценки рисков и управления ими во многих случаях (реально во всех нетривиальных ситуациях) не могут дать однозначных рекомендаций. В конце процесса принятия решения — всегда человек, менеджер, на котором лежит ответственность за принятое решение.
Поэтому процедуры энтропии естественно применять не только на конечном, но и на всех остальных этапах анализа рассматриваемого организацией проекта, используя при этом весь арсенал теории и практики энтропии.
Рассмотрим использования энтропии на примере прогноза погоды.
Пусть для некоторого пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того, что дождя не будет, равна 0,6. Пусть далее для этого же пункта вероятность дождя 15 октября равна 0,8, а вероятность отсутствия дождя в этот день — всего 0,2. Предположим, что определенный метод прогноза погоды 15 июня оказывается правильным в 3/5 всех тех случаев, в которых предсказывается дождь, и в 4/5 тех случаев, в которых предсказывается отсутствие осадков; в применении же к погоде 15 октября этот метод оказывается правильным в 9/10 тех случаев, в которых предсказывается дождь, и в половине случаев, в которых предсказывается отсутствие дождя (сравнительно большой процент ошибок в последнем случае естественно объясняется тем, что предсказывается маловероятное событие, предугадать которое довольно трудно). Спрашивается, в какой из двух указанных дней прогноз дает нам больше информации о реальной погоде?
Обозначим через β1
и β2
опыты, состоящие в определении погоды в рассматриваемом пункте 15 июня и 15 октября. Мы считаем, что эти опыты имеют всего по два исхода — В
(дождь) и  (отсутствие осадков); соответствующие таблицы вероятностей имеют вид: (отсутствие осадков); соответствующие таблицы вероятностей имеют вид:
Опыт β1
| исходы
|
В
|

|
| вероятн.
|
0,4
|
0,6
|
Опыт β2
| исходы
|
В
|

|
| вероятн.
|
0,8
|
0,2
|
Следовательно, энтропии опытов β1
и β2
равны
Н (β1
) = -0,4 log 0,4 — 0,6 log 0,6  0,97 бита, 0,97 бита,
Н (β2
) = - 0,8 log 0,8 - 0,2 log 0,2  0,72 бита. 0,72 бита.
Пусть теперь α1
и α2
— предсказания погоды на 15 июня и на 15 октября. Опыты α1
и α2
также имеют по два исхода: А (предсказание дождя) и 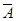 (предсказание сухой погоды); при этом пары опытов (α1,
β1
) и (α2
,β2
) характеризуются следующими таблицами условных вероятностей: (предсказание сухой погоды); при этом пары опытов (α1,
β1
) и (α2
,β2
) характеризуются следующими таблицами условных вероятностей:
Пара (α1,
β1
)
Пара (α2
,β2
)
( ). Эти таблицы позволяют определить также и неизвестные нам вероятности р1
(А
) и р1
( ). Эти таблицы позволяют определить также и неизвестные нам вероятности р1
(А
) и р1
( ),р2
(А
) и р2
( ),р2
(А
) и р2
( ) исходов А и ) исходов А и 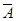 опытов α1
и α2
. По формуле полной вероятности имеем для опыта β1 опытов α1
и α2
. По формуле полной вероятности имеем для опыта β1
0,4=р(В)= р1
(А
)  + р1
( + р1
( ) ) =0,6· р1
(А
) +0,2· р1
( =0,6· р1
(А
) +0,2· р1
(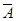 ) )
и для опыта β2
0,8 = р (В)= р2
(А
) 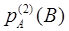 + р2
( + р2
( ) ) =0,9· р2
(А
)+0,5· р2
( =0,9· р2
(А
)+0,5· р2
(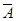 ). ).
Так как р1
( )= 1 — р1
(А
), р2
( )= 1 — р1
(А
), р2
( )= 1 — р2
(А
), то отсюда получаем )= 1 — р2
(А
), то отсюда получаем
р1
(А
)= р1
( )= 0,5, р2
(А
) = 0,75, р2
( )= 0,5, р2
(А
) = 0,75, р2
( ) = 0,25. ) = 0,25.
Подсчитаем теперь энтропии НА
(β1
), 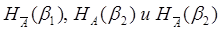 (в битах): (в битах):
НА
(β1
)= -0,6• log 0,6 - 0,4 • log 0,4  0,97, 0,97,
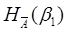 = - 0,2• log 0,2 – 0,8• log0,8 = - 0,2• log 0,2 – 0,8• log0,8  0,72 0,72
и
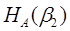 = - 0,9 • log 0,9 - 0,1• log 0,1 = - 0,9 • log 0,9 - 0,1• log 0,1 0,47, 0,47,
 = - 0,5 • log 0,5 - 0,5• log 0,5= 1. = - 0,5 • log 0,5 - 0,5• log 0,5= 1.
Следовательно,
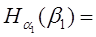 р1
(А
) НА
(β1
)+ р1
( р1
(А
) НА
(β1
)+ р1
( ) )  0,84, 0,84,
 р2
(А
) р2
(А
) 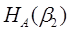 + р2
( + р2
( ) )  0,60. 0,60.
Таким образом, информация, содержащаяся в прогнозе погоды на 15 июня (опыт α1
) о реальной погоде в этот день (об опыте β2
), равна
I (α1,
β1
) = Н(β1
)
- 
 0,97 -0,84 = 0,13 бит, 0,97 -0,84 = 0,13 бит,
что несколько больше, чем информация о реальной погоде 15 октября (об опыте β2
), содержащаяся в прогнозе погоды на этот день (в опыте α2
):
I (α2,
β2
) = Н(β2
)
- 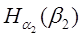
 0,72 — 0,60 = 0,12 бит. 0,72 — 0,60 = 0,12 бит.
Этот результат позволяет считать прогноз погоды па 15 нюня более ценным, чем прогноз на 15 октября, несмотря на то, что последний прогноз чаще оказывается правильным: действительно, в силу формулы полной вероятности, для прогноза погоды на 15 нюня вероятность оказаться правильным равна
р1
(А
) 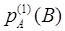 + р1
( + р1
( ) ) = 0,5• 0,6 + 0,5• 0,8 = 0,7, = 0,5• 0,6 + 0,5• 0,8 = 0,7,
в то время как для прогноза погоды на 15 октября эта вероятность равна
р2
(А
)  + р2
( + р2
( ) ) = 0,75 • 0,9 + 0,25 • 0,5 = 0,8. = 0,75 • 0,9 + 0,25 • 0,5 = 0,8.
Заключение
Энтропия как физическая переменная первично возникла из задач описания тепловых процессов. Впоследствии она стала широко использоваться во всех областях науки.
Информация - это знание, которое используется для развития, совершенствования системы и её взаимодействий с окружающей средой.
Информация сама развивается вслед за развитием системы. Новые формы, принципы, подсистемы, взаимосвязи и отношения вызывают изменения в информации, ее содержании, формах получения, переработки, передачи и использования. Благодаря потокам информации система осуществляет целесообразное взаимодействие с окружающей средой, т.е. управляет или управляема. Своевременная и оперативная информация может позволить стабилизировать систему, адаптироваться, восстанавливаться при нарушениях структуры и/или подсистем. От степени информированности системы, от взаимодействия системы и среды зависит развитие и устойчивость системы.
В современном мире все большее значение в управлении организацией отдается прогнозированию. Любая организация в процессе своей деятельности сталкивается с различными рисками, которые в большей или меньшей степени влияют на ее состояние. Многочислелны примеры ситуаций, связанных с социальными, технологическими, экономическими, политическими, экологическими и другими рисками. Именно в таких ситуациях обычно и необходимо прогнозирование. Известны различные виды критериев, используемых в теории принятия решений в условиях неопределенности (риска). Из-за противоречивости решений, получаемых по различным критериям, очевидна необходимость применения энтропии.
Список используемой литературы
1.
Дмитриев В.Н. Прикладная теория информации. М: Высшая школа,1989.
2.
Колмогоров А.Н. Теория информации и теория алгоритмов.М:Наука,1987.
3.
Колмогоров А.Н
. Три подхода к определению понятия “количество информации” // Проблемы передачи информации. 1965. Т.1. №1.
4.
Поплавский Р.П.
Депон Максвелла и соотношения между информацией и энтропией // УФН. 1979. Т. 128. Вып. 1.
5.
Хартли Р.
Передача информации// Теория информации и ее приложения. М.: Физматгиз. 1959.
6.
Шамбадаль П.
Развитие и приложения понятия энтропии . М.: Наука, 1967 .
7.
Яглом А.М., Яглом
И.М. Вероятность и информация. М.: Наука, 1973.
|