| Редуктор коническо-цилиндрический
Содержание задания: спроектировать привод к специальной установке
Кинематическая схема привода
1- электродвигатель, 2 – муфта, 3 – редуктор, 4 – муфта, 5‑исполнительное устройство, 6 – рама
Разработать:
1. Сборочный чертеж редуктора
2. Сборочный чертеж муфты
3. Сборочный чертеж привода
4. Рабочий чертеж корпусной детали
5. Рабочие чертежи детали.
Исполнительные устройства в зависимости от назначения и основных функциональных признаков работают широком диапазоне скорости и нагрузок. В качестве примеров использования ИУ можно привести: подъемный транспорт, металлургическое машиностроение, самолетостроение и др. Наиболее распространенным видом передач является зубчатая передача.
Общие сведения о редукторах
Если угловая скорость на выходе wдб
меньше угловой скорости на выходе wиу
, то передачу называют мультипликатором. Если wдб
> wиу
, то передачу называют редуктором. В связи с общей тенденцией повышения скоростей движения скоростей движения наибольшее распространение получили передачи, предназначенные для понижения угловых скоростей и соответствующего ему повышения моментов. Передаточное отношение редуктора определяется отношением угловых скоростей двигателя и ИУ.
Up = wдб
/ wиу
Пара сопряженных зубчатых колес в редукторе образуют ступень. Редукторы могут состоять из одной / одноступенчатые/ или нескольких / многоступенчатые/. Ступени могут быть составлены из разных колес. Выбор числа ступеней редуктора определяется передаточным отношением редуктора. Ступень редуктора, непосредственно соединенная с двигателем, называют быстроходной, а ступень, выходной вал которой соединен с ИУ – тихоходной. Параметрам ступеней присваивают индексы Б или Т. Меньшее зубчатое колесо ступени называют шестерней, большей – колесом. Параметрам шестерни присваивают индекс 1, параметрам колеса – индекс 2.
Виды редукторов
–
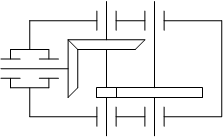
                               трехосный цилиндрический; трехосный цилиндрический; – трехосный цилиндрический;
– соосный;
– трехосный коническо-цилиндрический.
Выбор электродвигателя
Pиу
= P xz
xz
= xзб
+xзт
+ xм
2
+ xпп
3
= 0,98 * 0,98 * (0,99)2
= 0,975
Pиу
= 0,975 * 2,96 = 2,886 кВт
Потребная мощность не должна превышать номинальную мощность Pэв
более чем на 5%. Используя номограмму можно определить номинальную мощность Pэв.
Частота вращения И.У. nиу
= N2
= 67 об/мин, мощность p(NED) = 2.96 кВт, тип редуктора Электродвигатель марки 4A112MA6, номинальная мощность Pэв
= 3 кВт частота вращения ротора nэв
= N1 = 955 об/мин.
Передаточное отношение редуктора и распределение его по ступеням
Рассчитываем передаточное отношение для редуктора
Up = Uб Uт = n дв
/ nиу
= 955 / 67 = 14.25
Рассчитываем передаточное отношение для тихоходной ступени
Uт = a Up
k
;
коэффициенты при yт
= 0.8 соответственно a = 1,77; k = 0.298. Uт = 1.77*14.250.298
= 3.907
Рассчитываем передаточное отношение для быстроходной ступени.
Uб = Up/Uт = 14,25/3,907 = 3,64
Рассчитываем коэффициент рабочей ширины венца для быстроходной ступени.
yб
= 0,062 + 0,159 * Uб = 0.64
Рассчитываем угловые скорости
w1
,w2
,w3
. w1
=pnдв
/30, w1
=100.007 рад/с,
w3
= pnиу
/30 = 7,016 рад/с,
w2
=w1
/wб
= 27,412 рад/с.
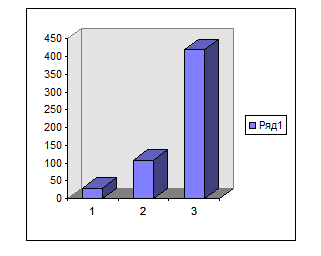
Крутящий момент на шестерни быстроходной ступени равен
T1б
= (1000P)/ w1
= (1000 *2.96)/100.007 = 29.597
Крутящий момент на шестерни промежуточной ступени равен
Tт1
=(1000*2,96)/27,412 =107,5
Крутящий момент на шестерни тихоходной ступени равен
Tт1
=(1000*2,96)/7,016 =419,6
| №
|
Наименование
|
Размерность
|
Символ
|
Б ступень
|
Т ступень
|
| 1
|
Передаточное отношение
|
-
|
U
|
3.648
|
3.907
|
| 2
|
Угловая скорость шестерни
|
рад/с
|
w1
|
100.007
|
100.007
|
| 3
|
Угловая скорость колеса
|
рад/с
|
w2
|
27.412
|
27.412
|
| 4
|
Крутящий момент
|
НМ
|
T1
|
29.598
|
105.281
|
| 5
|
Коэффициенты рабочей ширины
|
-
|
y
|
0.64
|
0.8
|
Подводимая мощность
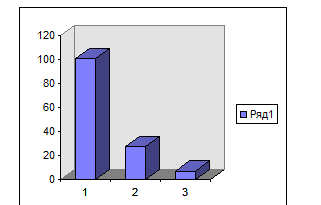
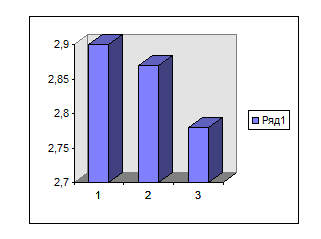
P1 = Pпотр * x муф = 2,96* 0,98 = 2,9
P2 = Pпотр * x муф xп п = 2,96* 0,98 * 0,99 = 2,87
P3 = Pпотр * x муф xпп x зац = 2,96* 0,98*0,99*0,97 = 2,78
Vp = 100.07/7.16 = 13.96
Vб = 100.007/27.412= 3.67
Vт = 27.412/7.16 = 3.82
Результаты выводов по кинематическим расчетам в виде диаграммы
Редукторная передача обеспечивает понижение круговых скоростей
При передаче мощности неизбежны ее потери
Вращающийся момент увеличивается
Расчет конической прямозубой передачи
Приближенное значение среднего диаметра шестерни
dm
1
(DM 11) = K1
K2
*(1.1 T1
(6.5‑U))1/3
= 13.446 *[1.1* 29,585* (6.5 – 3.648)]1/3
= 60.89 мм
K1
(COEF1) = 780/[G]2/3
н
= 780/58 = 13.446
K2
=1.0
Окружная скорость вращения зубчатых колес
V(V1) = (v1
dm
1
)/2000 = (100.007 * 60.89)/2000 = 3.04 м/с (8)
Частные коэффициенты нагрузки
KH
B
(KHB) = 1 + CH
(bw
/dw
1
)YH
= 1 + 0.339 (38/60.89)1.1
= 1.208; KFB
(KFB) = 1 + CF
(bw
/dw
1
)YF
= 1.419.
Уточненные значения среднего диаметра шестерни
dm1
(DM12) = K1
K2
[(T1
KHB
KHV
[U2
+1]1/2
)/(0.85Ybd
U)]1/3
= 13.446 [(29,585*1.208 *1.419*[3.648*3.648 +1]1/2
)/(0.85*0.64*3.648)]1/3
= 58.44
Предварительное значение рабочей ширины зубчатого венца
bw
(BW1) = Ybd
dm
1
= 0.64*58.44 = 37.5 = (BW2)
Конусное расстояние
Re
(RE1) = 0.5dm
1
[(U2
+1)1/2
Ybd
] = 0.5 * 58.44 *[(3.648*3.648 +1)1/2
+0.64] = 129.29
Модуль mte
, числа зубьев шестерни Z
1
и колеса Z
2
. mte
(MOD1) = 0.025*Re
= 0.025*129.29 = 3.23. Z1
(ZET11) = (2*Re
)/[mte
(U2
+1)1/2
] = 2*129.29/[3.23*(3.648*3.648 +1)1/2
] = 22.79. Z2
(ZET21)= Z1
U = 83.91. (ZET1)= 23, (ZET2) = 84
Реальное передаточное число Uд
и его отклонение от выбранного значения DU. Uд
(UREAL) = Z2
/Z1
= 3.65; DU (DELTU) =(Uд
- U)/U = 0.11
Геометрические параметры зубчатых колес:
d2
(DELT2) = arctg (Z2
/Z1
) = 74,6871
d1
(DELT1) = 90°
– d2
= 15,3129
de1
(DE1) = mte1
Z1
= 69,00
de2
(DE2) = mte2
Z2
= 252,00
dae1
(DAE1) = de1
+2mte
sin(d2
) = 74,79
dae2
(DAE2) = de2
+2mte
cos(d2
) = 253,58
Re
(RE) = 0.5 (de1
2
– de2
2
)1/2
= 160,64
dm1
(DM1) = de1
-bw
cos(d2
) = 58,96
Проверочный расчет на контактную прочность:
V(V)=(v1
dm1
)/(2000) = 3,04
Уточнение степени точности, коэффициента g-
Степень точности коэффициент нагрузки
Частные коэффициенты нагрузки.
KH
b
(KHB) = 1+CH
(bw
/dw1
)YH
= 1,208
KF
b
(KFB) = 1 + CH
(bw
/dw1
)YF
= 1,419
Удельная расчетная окружная сила
WHt
(WHT) = (2000*T1
KH
b
KHV
)/(bw
dm1
) = (2000 * 29,585*1.208*1.208)/(38 * 60.89) = 37.9
Расчетное контактное напряжение dн (REALH) = ZM
*ZH
* [(WHt
[Z1
2
+Z2
2
]1/2
)/(0.85dm
1
Z2
)]1/2
= 275 * 1.77 * [(37.9*[232
+ 842
]1/2
)/(0.85*60.89 * 84)] =431.02
Условие прочности на контактную выносливость.
dн/[d]H
=431.02/441.82 = 0.97 – условие прочности соблюдается
Недогрузка по контактной прочности
Ddн(DSIGH) = (1-dн/[d]H
) * 100% = 2.44%
Ширина колеса b2
и ширина шестерни b1
. b2
= b1
= bw
= 38
Проверочный расчет на изгиб:
Коэффициенты формы зубьев (выбирают в соответствии из таблицы в соответствии с коэффициентами
Z1
Z2
) УF
1
(УF1) = 3.9;
УF
1
(УF1) =3.6;
Zv1
(ZETV1) = Z1
/sin(d2
) = 23/sin (74.688) = 23.8; Zv2
(ZETV2) = Z2
/cos(d2
) = 84/ cos (74.688) = 318.12;
Частные коэффициенты нагрузки при изгибе
KFB
(KFB) = 1+CF
(bw
/dw
1
)YF
= 1+0.162 (38/60.89)1.37
= 1.419; KFV
(KFV) =1 +(KHV
- 1)*(dF
KH
a
KH
b
)/(dH
KF
a
KF
b
) = 1+(1.208–1)()/() = 1.424
Удельная расчетная окружная сила при расчете на изгиб
WFt
(WFT) = (2000 T1
KFB
KFV
)/(bw
dm
1
) = (2000 * 29,585 * 1.419 * 1.424)/(60.89*38) = 53.38
Средний модуль
mtm
(MODM)= dm
1
/Z1
=60.89/23 = 2.56
Расчетные напряжения изгиба для зубьев шестерни
dF
1
dF
2
. dF1
(REALF1) = (УF1
* WFt
)/(0.85mte
) = (3.94 * 53.38)/(0.85*2.56) = 96.50; dF2
(REALF2) = (УF2
* WFt)
/(0.85mte)
= (3.6 * 53.38) / (0.85 * 2.56) = 88.19
Расчет цилиндрической косозубой передачи
Приближенное значение начального диаметра шестерни.
dw
1
=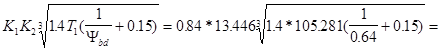 66.74; K1
(COEF1) = 66.74; K1
(COEF1) =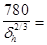 13.446; K2
=0.84 13.446; K2
=0.84
Окружная скорость вращения зубчатых колес
V(V1) =  = 0.91 (8,9) = 0.91 (8,9)
Частные коэффициенты нагрузки при расчете на контактною прочность
KH
a
= mV + l = 0.00814*0.91+1.051 = 1.111; KHB
(KHB1) = 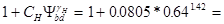 1.059; KHV
(KHV1) = 1.059; KHV
(KHV1) = =1.012 =1.012
Утоненное значение начального диаметра шестерни
dw
1
(DW12) = 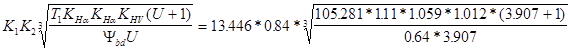 = 65.69 = 65.69
Предварительное значение рабочей ширины зубчатого венца
bw
(BW1) = Ybd
dw
1
= 0.64*65.69 = 52.55; BW = BW2=BW1 = 53;
Межосевое расстояние
aw
(AW1) = 0.5dw
1
(U+1)=0.5*65.69 (0.64+1) = 161.17; AW = 160;
Модуль, угол наклона зубьев В и числа зубьев шестерни Z1
и колеса Z2
m(MOD1) = 0.02aw
= 3.2; MOD = 3; 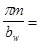 0.17; b1
(BETA1)=10.243; Zå
1
(ZETE1)= 0.17; b1
(BETA1)=10.243; Zå
1
(ZETE1)= 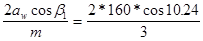 =104.97; Zå
= 104; b= =104.97; Zå
= 104; b= 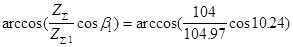 =12.8384; Z1
(ZET11)= =12.8384; Z1
(ZET11)= 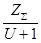 =21.19; ZET1 = 21; Z2
(ZET2) = Zå
- Z1
=83 =21.19; ZET1 = 21; Z2
(ZET2) = Zå
- Z1
=83
Реальное передаточное число и его отклонение от выбранного значения
Uд
(UREAL)=  =3.95; DU(DELTU)= =3.95; DU(DELTU)=  = 1.16; = 1.16;
Геометрические размеры зубчатых колес:
dw
1
(DW1) =(mZ1
)/(cosB) =
dw2
(DW2) = (mZ2
)/(cos B) =
da1
(DA1) = dw1
+ 2m =
da2
(DA2) = dw2
+ 2m =
Проверочный расчет на контактную прочность
V(V) = 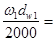 0.89 0.89
Уточнение степени точности
m=0.00814; l = 1.051; g0
=8;
Частные коэффициенты нагрузки
KH
a
= mV + l = 0.00814*0.91+1.051 = 1.111; KHB
(KHB1) = 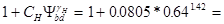 1.061; KHV
(KHV1) = 1.061; KHV
(KHV1) = = 1.011 = 1.011
Удельная расчетная окружная сила
WHt
(WHT)=  =73.23 =73.23
Расчетное контактное напряжение
ZM
(ZM)=275; ZH
(ZH)=1.764Cosb0.872
= 1.728; ZE
(ZE)= 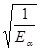 =0.779; Eb
= 1.25; Ea
= 1.647; dH
(REALH) = ZM
ZH
ZE
* =0.779; Eb
= 1.25; Ea
= 1.647; dH
(REALH) = ZM
ZH
ZE
* 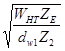 =441.22; =441.22;
Условие прочности на контактную выносливости
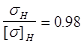
Недогрузка на контактной прочности
DdH
(DSIGH)= 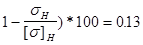 ; ;
Ширина колеса b2
и ширина шестерни
b1
. b2
(B2) = bw
= 53; b1
(B11)=b2
+0.6*  =53+0.6 =53+0.6  =57.37; (B1)=58; =57.37; (B1)=58;
Проверочный расчет на изгиб:
Коэффициенты формы зубьев шестерни и колеса
ZV
1
(ZETV1)= 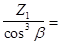 22.66; ZV
2
(ZETV2)= 22.66; ZV
2
(ZETV2)= 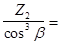 89.55; YF
1
(YF1) = 3.98; YF
2
(YF2)=3.6; 89.55; YF
1
(YF1) = 3.98; YF
2
(YF2)=3.6;
Частные коэффициенты нагрузки при расчете на изгиб
KF
b
(KHB) = 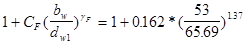 = 1.123; KFV
(KFV)= = 1.123; KFV
(KFV)=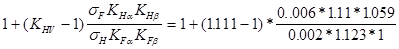 =1.034; =1.034;
Удельная расчетная окружная сила при расчете на изгиб
WFt
(WFT) =  = 71.44 = 71.44
Расчетные напряжения изгиба. YE
(YEPS)=1; Yb
(YBET) = 0.91
dF1
(REALF1)= 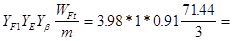 86.08<[d]F1
; dF2
(REALF2)= 86.08<[d]F1
; dF2
(REALF2)= 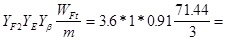 77.87<[d]F2
; 77.87<[d]F2
;
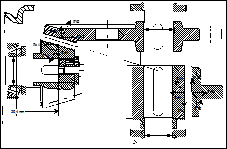
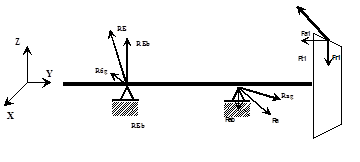
Реакции от сил в плоскости от XOZ:
å MA
=0;
Ft
l1
-Rbg
l2
=0;
Rbg
=(Ft
l1
)/l2
= (1003.92*45.7) 99.5 =461.09
å MB
=0;
Ft
(l1
+l2
) – Rag
l2
=0;
Rag
= Ft
(l1
+l2
) / l2
= 1003.92 (45.7+99.5)/ 99.5 = 1465.01
Проверка найденных сил:
å X = -1003.92 +1465 – 461.09 = 0
Все силы найдены правильно
Реакции от сил в плоскости YOZ:
å Ma
= 0;
Fa1
dm1
/2 – Rbb
l2
– Fr1
l1
= 0;
Rbb
=(Fa1
dm1
/2 – Fr1
l1
)/l2
=(96.5 * 27.5 – 352.42 * 45.7)/99.5 =-135.19
å Mb
=0;
Fa1
dm1
/2 – Fr1
(l1
+l2
) – Rab
l2
= 0;
Rab
= (Fa1
dm1
/2 – Fr1
(l1
+l2
))/l2
=
(96.50*27.5 – 352.42 (45.7+99.5))/99.5 =-487.61
Проверка полученных результатов:
å Y = 1570.12 – 353.467 -1216.48 = 0;
RrB
=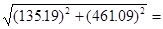 480,5 480,5
RrA
=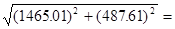 1544.02 1544.02
Построение эпюр моментов
Плоскость YOZ
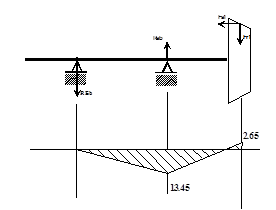
сечение B: Мx
+Rbb
x = 0;
Мx
= – Rbb
x
x=0 -> Mx
= 0; x=l2
= 99.5 -> Mx
= -13.45
сечение A: MX
+Rbb
(x+l2
) – Rab
x = 0
MX
= – Rbb
(x+l2
) + Rab
x
Mx
= x(Rab
– Rbb)
– Rl2
x =0 -> Mx
= -13.45; x=l1
= 45.7 ->Mx
= 2.65
Горихзонтальная плоскость XOY
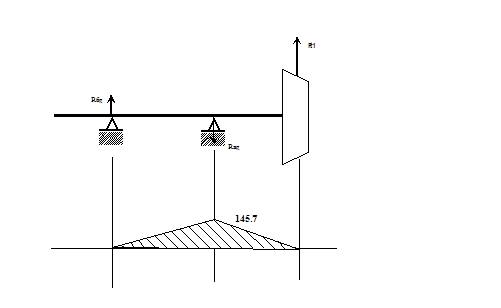
сечение B Мx
= 0;
сечение A MX
= Rag
l2
= 1465.01*99.5 = 145.7
сечение E Mx
= Rag
l2
-Ft
(l1
+l2
) =145.7 – 145.7 = 0;
Расчет промежуточного вала:
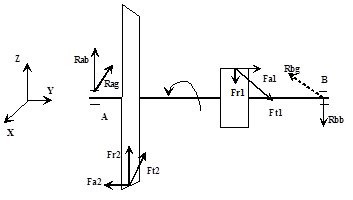
Реакции опор в плоскости XOY:
å MA
=0;
Rbg
(l1
+l2
+l3
) – Ft2
*l1
– Ft1
(l1
+l2
)=0;
Rbg
=(Ft2
*l1
+ Ft1
(l1
+l2
))/(l1
+l2
+l3
) = 2333.8
å MB
=0;
Rag
(l1
+l2
+l3
) +Ft1
*l3
+Ft2
(l2
+l3
) =0;
Rag
= (-Ft1
*l3
– Ft2
(l2
+l3
))/(l1
+l2
+l3
) = -1928.79
Проверка найденных сил:
å X = -1928.79–2333.8 +3258.69+1003.92 = 0
Реакции опор в плоскости ZOY:
å MA
=0;
– Fa2
*d1
/2+Fr2
*l1
-Fr1
*(l1
+l2
) – Fa1
*d2
/2 – Rbb
*(l1
+l2
+l3
) =0;
Rbb
=(-Fa2
*d1
/2+Fr2
*l1
-Fr1
*(l1
+l2
) – Fa1
*d2
/2)/(l1
+l2
+l3
) = -977.96
å MB
=0;
– Fa2
*d1
/2 – Fr2
*(l2
+l3
)+Fr1
*l3
– Fa1
*d2
/2 – Rab
*(l1
+l2
+l3
)=0;
Rab
= (-Fa2
*d1
/2 – Fr2
*(l2
+l3
)+Fr1
*l3
– Fa1
*d2
/2)/(l1
+l2
+l3
) = 141.99
Проверка найденных сил:
å X = 141.99 +977.96+96.5–1216.48 = 0
RrB
= 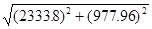 =2530.38; =2530.38;
RrA
= 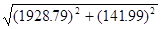 = 1934 = 1934
Построение эпюр моментов:
В плоскрсти ZOY

Сечение А: Mx
– Rab
x = 0
Mx
= Rab
x
x=0 -> Mx
=0; x =l1
= 42.5 -> Mx
= 6.03
Сечение E: Mx
– Rab
(l1
+x) – Fa
2
d1
/2 – Fr
2
x =0
Mx
= Rab
(l1
+x) + Fa2
d1
/2 + Fr2
x =0
Mx
= x(Rab
+ Fr2
) +Rab
l1
+ Fa2
d1
/2
x = 0 -> Mx
= 29.99; x = l2
= 60.5 ->Mx
= 44.41
Сечение B: Mx
– Rab
(l1
+l2
+x) – Fr2
(l2
+x) – Fa2
d1
/2 – Fa1
d2
/2 +Fr1
x = 0
Mx
= Rab
(l1
+l2
+x)+Fr2
(l2
+x) + Fa2
d1
/2 +Fa1
d2
/2 – Fr1
x
Mx
= x(Rab
+Fr2
– Fr1
) + l1
Rab
+l2
(Rab
+Fr2
) + Fa2
d1
/2 +Fa1
d2
/2
x = 0 -> Mx
= 57.77; x = l3
= 59.1 -> Mx
= 0
В плоскости XOY:

Сечение A: Mx
– Rag
x = 0
Mx
= Rag
x
x = 0 -> Mx
= 0; x=l1
= 42.5 -> Mx
= 81,97
Сечение E: Mx
– Rag
(l1
+ x) + Fr
2
x – Fa
2
d1
/2 = 0
Mx
= Rag
(l1
+ x) – Ft2
x +Fa2
d1
/2
Mx
= x(Rag
– Ft2
) + Rag
l1
+Fa2
d1
/2
x = 0 -> Mx
= 105.93; x = l2
= 60.5 -> Mx
= 161.25
Сечение B: Mx
– Rag
(l1
+l2
+x) + Ft2
(l2
+x) +Fr1
x – Fa2
d1
/2 +Fa1
d2
/2 = 0
Mx
= x(Rag
– Ft2
– Ft1
) +l1
Rag
+l2
(Rag
– Ft2
) +Fa2
d1
/2 – Fa1
d2
/2
x= 0 -> Mx
=; x = l3
= 59.1 -> Mx
= 0
Расчет тихоходного вала:
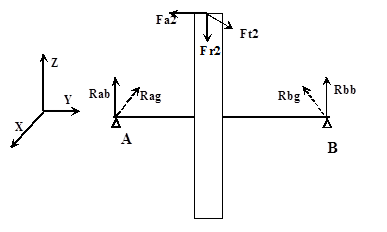
Реакции опор в плоскости ZOY:
å MA
= 0
Rbb
(l1
+l2
) + Fa2
d/2 – Fr2
l1
= 0
Rbb
=(Fr2
l1
- Fa2
d/2)/(l1
+l2
)
Rbb
= (128.58 – 94.8)/(164.9) = 204.851
å MB
= 0
– Rab
(l1
+l2
) +Fa2
d/2 +Fr2
l2
= 0
Rab
= (Fa2
d/2 +Fr2
l2
)/(l1
+l2
)
Rab
= (94.8+)/164.9 = 1011.6
Проверяем найденные реакции:
Rab
+ Rbb
-Fr
2
= 1011.6 + 204.8 – 1216.48 = 0
Все силы направленны правильно
Реакции опор в плоскости XOY:
å MA
= 0
Rbg
(l1
+l2
) – Ft2
l1
+ Fa2
d/2 =0
Rbg
= (Ft2
l1
- Fa2
d/2) /(l1
+l2
)
Rbg
= (344.7 – 94.8)/164.9 = 1513.9
å MB
= 0
– Rag
(l1
+l2
) + Fa2
d/2 +Ft2
l2
=0
Rag
= (Fa2
d/2 +Ft2
l2
)/(l1
+l2
)
Rag
= (94.8 +)/164.9 = 1744.7
Проверяем найденные реакции:
– Rag
– Rbg
+ Ft
2
= -1513.9 – 1744.7 + 3258.69 = 0
Все силы направленны правильно
RrB
=  =1527.68; =1527.68;
RrA
= 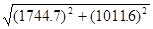 = 2016.75; = 2016.75;
Построение эпюр моментов:
В плоскости ZOY:

Сечение А: Mx
– Rab
x = 0
Mx
= Rab
x
x = 0 -> Mx
= 0; x=l1
= 105.7 -> Mx
= 106.92
Сечение B: Mx
– Rab
(l1
+x) +Fr
2
x + Fa
2
d/2 = 0
Mx
= Rab
(l1
+x) – Fr2
x – Fa2
d/2
Mx
= x(Rab
– Fr2
) + Rab
l1
– Fa2
d/2
x = 0 -> Mx
= 12.11; x = l2
= 59.2 -> Mx
= 0
В плоскости XOY:

Сечение А: Mx
– Rag
x = 0
Mx
= Rag
x
x = 0 -> Mx
= 0; x=l1
= 105.7 -> Mx
= 184.41
Сечение B: Mx
– Rag
(l1
+x) +Ft
2
x + Fa
2
d/2 = 0
Mx
= Rag
(l1
+x) – Ft2
x – Fa2
d/2
Mx
= x(Rag
– Ft2
) + Rag
l1
– Fa2
d/2
x = 0 -> Mx
= 89.61; x = l2
= 59.2 -> Mx
= 0
Расчет сечения на статическую прочность
Предположительно опасным сечением является сечение B в тихоходном валу.
Результирующий изгибающий момент:
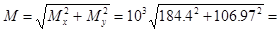 213,18*103
H*мм 213,18*103
H*мм
Осевой момент сопротивления сечения:
 = 8362 мм 3 = 8362 мм 3
Эквивалентное напряжение:
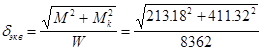 =55.4 =55.4
Коэффициент запаса прочности текучести при при коэффициенте перегрузки Kп
=2.5
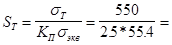 3.9 >[St
] = 1.6 3.9 >[St
] = 1.6
Расчет сечения В на сопротивление усталости.
Определяем амплитуду цикла в опасном сечение:
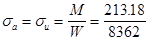 = 25.49Н/мм2 = 25.49Н/мм2
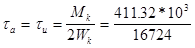 =12.29Н/мм2 =12.29Н/мм2
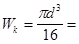 16724 16724
Принимаем Ks
/Kd
= 3; Kt
/Kd
= 2.2; KF
= 1; KV
= 1.034
Коэффициенты концентраций напряжений
(Ks
)D
= 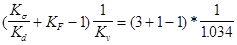 =2.9 =2.9
(Kt
)D
=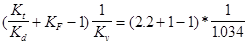 =2.127 =2.127
Пределы выносливости вала:
(s-1
)D
=  120.68 120.68
(t-1
)D
= 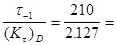 98.73 98.73
Коэффициенты запаса по нормальным и касательным напряжениям
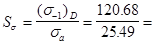 4.73 4.73
 8.03 8.03
Коэффициент запаса прочности в сечение В
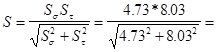 4.07 >[s]=2.1 4.07 >[s]=2.1
Сопротивление усталости в сечение Е обеспечивается.
Расчет подшибников.
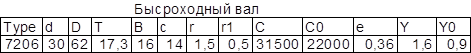
Определение осевых нагрузок:
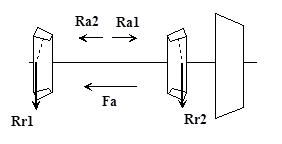
Rr1
= RrB
= 480.5; Rr2
= RrA
= 1544.02; Fa
= Fa1
= 96.5
Определяем осевые составляющие:
Rs
1
= 0.83 * e * Rr
1
= 0,83* 0.36 * 480.5 = 143.57
Rs
2
= 0.83 *0.36 * 1544.02 = 461.35
Так как Rs
1
<Rs
2
и Fa
< Rs
2
– Rs
1
, то в соответствии с таблицей находим осевые силы, нагружающие подшипники:
Ra2
= Rs2
= 461.35; Ra1
= Ra2
– Fa
= 461.35 – 96.5 = 364.85
Отношение:
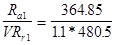 = 0.69 > e=0.36 => X=0.4; Y =0.4ctg(a) = 1.49 = 0.69 > e=0.36 => X=0.4; Y =0.4ctg(a) = 1.49
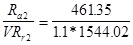 = 0.27 < e = 0.36; => X=1; Y = 0 = 0.27 < e = 0.36; => X=1; Y = 0
Эквивалентная нагрузка:
Принимаем следующие сонстанты: v = 1.1; Kб
=1.5; KT
=1.2;
RE1
=(XVRr1
+ YRa1
) KБ
KT
RE1
= (0.4*1.1*480.5 + 1.49* 364.85) 1.5*1.2
RE1
= 1359.08
RE2
=XVRr2
KБ
KT
RE2
=1*1.1*1544.02*1.5*1.2 = 3057.15
Расчитываем долговечность более нагруженного подшибника опоры 2 при a23
= 0.65:
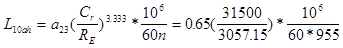 =26981 ч =26981 ч
Требуемая долговечность 10000 ч, выбранный подшибник подходит по долговечности.
Расчет подшибников для промежуточного вала
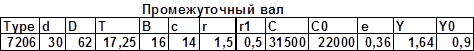
Определение осевых нагрузок:
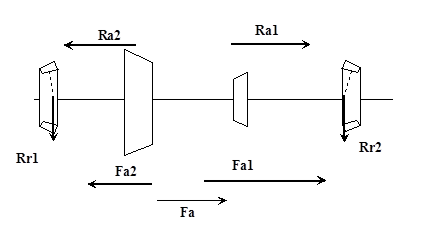
Rr1
= RrA
= 1934;
Rr2
= RrB
= 2530.38;
Fa
= Fa1
– Fa2
= 742.66 – 352.42 = 390.24
Определяем осевые составляющие:
Rs
1
= 0.83*e*Rr
1
= 0,83*0.36*1934 = 577,87
Rs
2
= 0.83*e*Rr
1
= 0.83*0.36 * 2530.38 = 756
Так, как Rs
1
<Rs
2
и Rs
2
– Rs
1
< Fa
находим осевые силы нагружающие подшибники:
Ra1
= Rs1
= 577.87;
Ra2
= Ra1
+Fa
= 577.87 + 390.24 = 968.11;
Отношение:
 = 0.27 < e = 0.36 => X= 1; Y =0 = 0.27 < e = 0.36 => X= 1; Y =0
 = 0.37 < e = 0.36; => X=0.4; Y = 1.49 = 0.37 < e = 0.36; => X=0.4; Y = 1.49
Эквивалентная нагрузка:
Принимаем следующие сонстанты: v = 1; Kб
=1.2; KT
=1;
RE1
=XVRr1
KБ
KT
RE1
= 1*1*1934* 1.2*1. = 2320
RE2
=XVRr2
KБ
KT
RE2
=(0.4*2530.38 +1.49* 968) *1.2 *1= 2945
Расчитываем долговечность более нагруженного подшибника опоры 2 при a23
= 0.65:
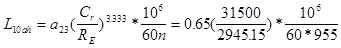 =30560 ч =30560 ч
Требуемая долговечность 10000 ч, выбранный подшибник подходит по долговечности.
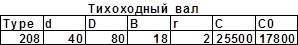
Осевые составлябщие для радиальных подшибников RsB
= RsA
= 0
Из условия равновесия вала RaB
= 0; RaA
= Fa
= 742.66
Для опоры B: X=1; Y=0
Для опоры A отношение: = 0.113 = 0.113
X=0.56; Y = 1.45; e = 0.3
Отношение 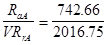 = 0.36 > e = 0.3 = 0.36 > e = 0.3
Эквивалентные динамические нагрузки при KБ
=1.2 и КТ
= 1
RE1
= (VXRrA
+YRaA
) KБ
КТ
RE1
=(0.56 * 2016.75 + 1.45 * 742.66) 1.2=2647.48
RE
2
= VXRrB
KБ
КТ
RE
2
= 1* 1527.68 *1.2 = 1833.216
Расчитываем долговечность более нагруженного подшибника опоры A при a23
= 0.65:
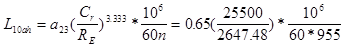 =21550 ч =21550 ч
Требуемая долговечность 10000 ч, выбранный подшибник подходит по долговечности.
Смазка
Выбор смазочного материала основан на опыте эксплуатации машин. Принцип назначения сорта масла следующий: чем выше контактное давление в зубьях, тем с большей вязкостью должно обладать масло, чем выше окружная сила колеса, тем меньше должна быть вязкость масла.
Вязкость масла определяют от контактного напряжения и окружной скорости колес.
Из таблицы выбираем сорт масла учитывая перечисленные выше параметры. Исходя из полученных результатов расчета редуктора выбираем масло И-Г-С‑68. Оно наиболее подходит для данного типа редуктора! В коническо-цилиндрических редукторах в масляную ванну должны быть обязательно погружены зубья конического колеса.
Подшипники смазываются тем же маслом, что и детали передач.
При работе передач масло постепенно загрязняется продуктами работы передач. С течением времени масло стареет. Его свойства ухудшаются. Для контроля количества и состояния используют специальный масломер.
|