Учреждение образования «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
КУРСОВОГО ПРОЕКТА
Тема:
"Водяной насос"
Минск 2007
Введение
Создание современной машины требует от конструктора всестороннего анализа проекта. Расходы на изготовление и эксплуатацию должны быть минимальными, но обеспечивающими достижениезаданных параметров. Из допустимого множества решений конструктор выбирает компромиссное решение с определенным набором параметров и проводит сравнительную оценку различных вариантов. Выделяют главные критерии, а вспомогательные показатели используют как ограничения, накладываемые на элементы решения. Единой системой конструкторской документации (ЕСКД) установлено 5 стадий разработки документации на изделия всех отраслей промышленности: техническое задание, техническое предложение, эскизный проект, технический проект и разработка рабочей документации.
Основная цель курсового проектирования – привить навыки использования общих методов проектирования и исследования механизмов для создания конкретных машин и приборов разнообразного назначения. Курсовое проектирование ставит задачи усвоения студентами определенных методик и навыков работы по направлениям:
– оценка соответствия структурной схемы механизма основным условиям работы механизма или прибора
– проектирование структурной и кинематической схемы рычажного механизма по заданным основным и дополнительным условиям
– анализу режима движения механизма при действии заданных сил
– учет сил трения в кинематических парах и определение коэффициента полезного действия
– проектирование зубчатых рядовых и планетарных механизмов
– расчет оптимальной геометрии зубчатых зацеплений выходного звена
– разработка циклограмм и тактограмм для систем управления механизмами
– определение мощности и выбор типа движения.
Задание на курсовое проектирование содержит название темы проекта, краткое описание назначения машины или прибора и функции их исполнительных органов и элементов, схемы согласованности перемещений исполнительных органов, исходные данные.
1.
Динамический синтез рычажного механизма
1.1 Задачи и методы динамического синтеза и анализа машинного агрегата
Насос:
Процессы в водяных насосах осуществляются за период одного оборота кривошипа.
Принципы работы водяного насоса
.
Одноцилиндровый поршневой насос предназначен для перекачивания жидкости. Движение от электродвигателя передается кривошипу через планетарный редуктор и зубчатую передачу. Преобразование вращательного движения кривошипа в возвратно-поступательное движение поршня осуществляется трехзвенным рычажным кулисным механизмом, состоящим из кривошипа, шатуна и ползуна (поршня). Всасывание жидкости в цилиндр происходит через впускной клапан во время хода поршня вверх при давлении ниже атмосферного. Нагнетание жидкости происходит через выпускной клапан при ходе поршня вниз. Смазывание механизмов насоса осуществляется плунжерным масляным насосом кулачкового типа. Кулачек закрепленный на одном валу с зубчатым колесом приводит в движение толкатель. Равномерное движение обеспечивает маховик.
Таблица 1.1 – исходные данные
| параметр |
значение |
единица измерения |
| nk |
300 |
об/мин
|
| H |
115 |
мм
|
| l |
0.22 |
- |
| Pmax |
0.8 |
M
П
a
|
| d |
0.09 |
- |
| q |
30 |
к
г/м
|
| d |
230 |
мм
|
| ε |
0.2 |
- |
Массы звеньев:  ; ;  ; ; 
Моменты инерции: 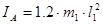 ; ; 
1.2 Структурный анализ механизма
1.2.1 Перечень звеньев механизма
1. – кривошип; 2. – шатун; 3 – ползун.
1.2.2 Перечень кинематических пар
0–1 – кинематическая пара 5-го класса, вращательная;
1–2 – кинематическая пара 5-го класса, вращательная;
2–3 – кинематическая пара 5-го класса, вращательная;
3–0 – кинематическая пара 5-го класса, поступательная;
1.3 Определение степени подвижности механизма
Степень подвижности механизма определим по уравнению Чебышева
W= 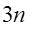 - -  - - 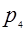
где 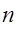 – количество движущихся звеньев механизма; – количество движущихся звеньев механизма;
Для механизма, что исследуется, 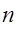 =3, кинематических пар 5-го класса =3, кинематических пар 5-го класса  =4, кинематические пары 4-го класса отсутствуют. =4, кинематические пары 4-го класса отсутствуют.
Имеем: W=3×3–2×4=1.
Для работы механизму необходима только одно ведущее звено, так как степень подвижности равна единице.
1.4 Определение недостающих размеров
1.4.1 Определение длины
Определим длину l
1
и l
2
, которые находятся из следующего неравенства:
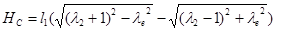 (1) (1) 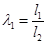 ; ; 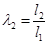
 ; ;  ; ;  ; ; 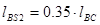 ; ;
из формулы (1) 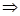 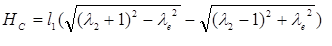
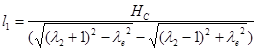
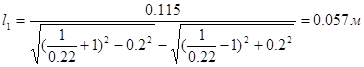 ; ; 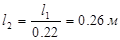
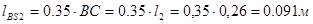
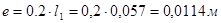
1.4.2 Определяем угловую скорость
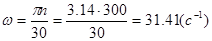
1.4.3 Определим массы звеньев
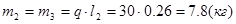
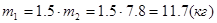
1.5 Описание определения кинематических характеристик рычажного механизма
В левой части чертежа строим планы положений механизма. За начальное положение механизма принимаем положение, когда кривошип и шатун находятся в мертвом положении (вытянуты в одну линию). Затем строим 12 равноотстоящих положений входного звена (кривошипа АВ). Для выполнения построений планов положений механизма предварительно определяем масштабный коэффициент длины.
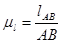
 -действительная длина звена АВ, м -действительная длина звена АВ, м
АВ – отображающий ее отрезок на чертеже, мм
Принимаем АВ=60 мм.
 ; ; 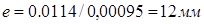
 ; ;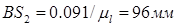

Планы скоростей
Для построения планов скоростей воспользуемся векторными уравнениями для построения планов скоростей.
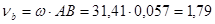 (м/с) (м/с)
Введем масштабный коэффициент скорости  (м/мм*с) (м/мм*с)
pb
= vb
/ μv
=  =
71,6мм
=
71,6мм
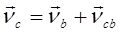
Вектор скорости точки В
перпендикулярен звену АВ, вектор скорости точки С
направлен по направлению движения поршня 3, вектор скорости точки С
относительно точки В
перпендикулярен звену ВС
.
Для построения отрезкаps2
, изображающего вектор скорости центра масс S2
, воспользуемся теоремой подобия:
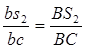 ; ;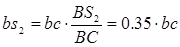
Измеряем на планах скоростей длины соответствующих векторов и полученные значения записываем в таблицу 1.2.
Таблица 1.2
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| pc, мм |
0 |
42,9 |
69,6 |
72,2 |
55 |
28,1 |
1,1 |
29,8 |
55,2 |
71 |
68,3 |
42,4 |
| bc, мм |
71,6 |
63,9 |
39 |
2,6 |
34,5 |
61,4 |
71,6 |
63,3 |
38,4 |
2,6 |
33,9 |
60,8 |
| ps2
, мм |
46,5 |
55,1 |
68,4 |
71,8 |
64,2 |
52,4 |
46,6 |
52,3 |
63,7 |
71,4 |
68,5 |
55,9 |
1.6 Построение диаграмм
Вычерчиваем заданную индикаторную диаграмму, под линией движения ползуна. Масштабный коэффициент длин принимаем таким же как и для планов перемещений  . .
Максимальную ординату на графике давления принимаем равной 50 мм, тогда 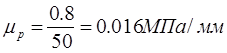 . .
Полный цикл водяного насоса совершается за 1 оборот кривошипа.
Значение силы полезного сопротивления FC
определяем по формуле: 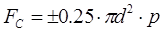 . .
Знак «+» берется в том случае, когда сила FC
направлена противоположно движению ползуна.
Определяем значения давлений и сил сопротивления для всех положений кривошипа. Результат заносим в таблицу 1.3.
Таблица 1.3
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Pi
, МПа |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0,8 |
0,8 |
0,8 |
0,8 |
0,8 |
0,8 |
| FCi
,H |
830 |
830 |
830 |
830 |
830 |
830 |
33221 |
33221 |
33221 |
33221 |
33221 |
33221 |
Строим диаграмму аналогов скоростей рабочего звена, принимая максимальную ординату 150 мм.
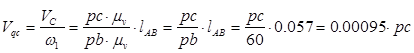
Результаты заносим в таблицу 1.4.
Таблица 1.4
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| vqc
, мм |
0 |
0,049 |
0,069 |
0,071 |
0,054 |
0,027 |
0,001 |
0,029 |
0,054 |
0,070 |
0,068 |
0,042 |
Принимаем масштабный коэффициент: 
Строим диаграмму аналогов скоростей выходного звена в зависимости от угла поворота кривошипа.
1.7 Динамическая модель машинного агрегата
В связи с необходимостью в данном проекте выполнения динамического анализа кривошипно-ползунного механизма целесообразно динамическую модель машинного агрегата представить в виде вращающегося звена (звена приведения), закон движения которого был бы таким же, как и у кривошипа 1 механизма, т.е.  , , 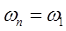 , , 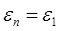 . .
Приведенный момент сил Mn
представим в виде:

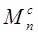 -приведенный момент сил сопротивления. -приведенный момент сил сопротивления.
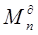 -приведенный момент движущих сил, принимается в проекте постоянный. -приведенный момент движущих сил, принимается в проекте постоянный.
Приведенный момент инерции агрегата 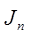 определяется из условия равенства кинематической энергии звена приведения и кинетической энергии звеньев машинного агрегата, характеризуемых переменными по величине аналогами скоростей, а приведенный момент Мn
находится из условия равенства элементарных работ этого момента и тех действующих сил, которые приводятся к звену приведения. определяется из условия равенства кинематической энергии звена приведения и кинетической энергии звеньев машинного агрегата, характеризуемых переменными по величине аналогами скоростей, а приведенный момент Мn
находится из условия равенства элементарных работ этого момента и тех действующих сил, которые приводятся к звену приведения.
1.8 Расчет приведенных моментов инерции
За звено приведения примем кривошип АВ.
Общая формула для определения приведенного момента инерции звеньев имеет вид:
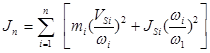
В моем курсовом проекте эта формула будет следующей:

Отношение скоростей есть передаточные функции, которые определяются из планов скоростей.
Введем обозначения:
 ; ; ; ;


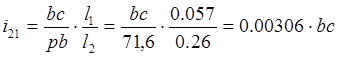
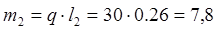 кг кг
 кг кг
 кг кг
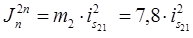

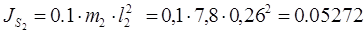 кг кг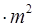
 кг кг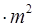
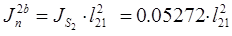
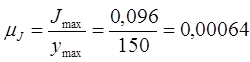 кг*м2
/мм кг*м2
/мм
Результаты вычислений приведены в таблице 1.5. По этим же данным строим диаграмму приведенного момента инерции механизма.
Таблица 1.5
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| J
п
, кг*м2
|
0,058 |
0,071 |
0,092 |
0,096 |
0,080 |
0,064 |
0,058 |
0,065 |
0,080 |
0,094 |
0,091 |
0,071 |
По оси абсцисс принимаем масштабный коэффициент:
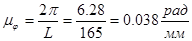
где L – длина отрезка оси абсцисс, соответствующая углу 2π рад.
1.9 Расчёт приведенных моментов сил сопротивления
Определяем приведенный к валу кривошипа момент 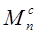 от сил сопротивления, при этом учитываем действие сил от сил сопротивления, при этом учитываем действие сил 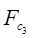 , , 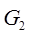 , ,  . Силу веса кривошипа . Силу веса кривошипа  учитывать не следует, так как ее работа равна нулю (центр тяжести кривошипа совпадает с осью вращения – его скорость равна нулю) и приведенный момент от нее равен нулю. учитывать не следует, так как ее работа равна нулю (центр тяжести кривошипа совпадает с осью вращения – его скорость равна нулю) и приведенный момент от нее равен нулю.
Приведенный момент найдем из условия и равенства мощностей приведенного момента и приводимых сил:
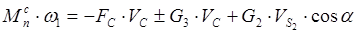
α-угол между направлением силы  и направлением скорости и направлением скорости  центра тяжести центра тяжести 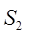 . .
Знак «+» перед мощностями сил веса и сил сопротивлений будем ставить тогда, когда эта сила является силой сопротивления; знак «–» перед движущими силами.
Окончательно получим:
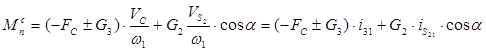
Fc
[1–6] = 830 H
Fc
[7–12] = 33221 H
G
2
= m
2
*g
= 7.8*9.81 = 76,518 H
G
3
= m
3
*g
= 7.8*9.81 = 76,518 H
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| cos α
|
0.034 |
-0.669 |
-0.933 |
-0.999 |
-0.939 |
-0.656 |
-0.034 |
0.615 |
0.920 |
0.999 |
0.951 |
0.707 |
Результаты заносим в таблицу 1.6.
Таблица 1.6
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Mпр
,
Hм
|
-0,0955 |
-23,308 |
-37,5718 |
-36,641 |
-29,09 |
-14,64 |
-28,89 |
-778,34 |
-1441,8 |
-1854,7 |
-1784,4 |
-1107,8 |
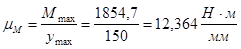
1.10 Определение работы сил сопротивления А и движущих сил Аg
Так как работы сил сопротивления равны  ,то график ,то график 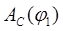 строим методом численного интегрирования графика строим методом численного интегрирования графика 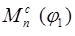 по формуле трапеции: по формуле трапеции:

 - шаг интегрирования - шаг интегрирования
Результаты заносим в таблицу 1.7
Таблица 1.7
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1» |
| А, Дж |
0 |
-6,12 |
-22 |
-41,4 |
-58,6 |
-70 |
-81,38 |
-292,6 |
-873,4 |
-1735,9 |
-2688 |
-3444,7 |
-3734,5 |
 Дж/мм Дж/мм
1.11 Построение графика изменения кинетической энергии и диаграммы «энергия-масса»
Для построения графика изменения кинетической энергии поступаем следующим образом: вычитаем ординаты графика 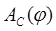 из соответствующих ординат графика из соответствующих ординат графика 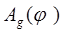 и строим график суммарной (избыточной) работы и строим график суммарной (избыточной) работы 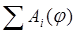 , который одновременно является графиком изменения кинетической энергии механизма и приведенного момента инерции. , который одновременно является графиком изменения кинетической энергии механизма и приведенного момента инерции.
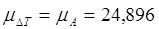 Дж/мм Дж/мм
1.12 Определение параметров маховика
Для определения момента инерции маховика по закону коэффициента неравномерности движения δ следует провести касательные к графику «энергия-масса» под углами ψmax
и ψmin
к оси абсцисс (оси приведенного момента инерции) тангенсы которых определяются по формуле:
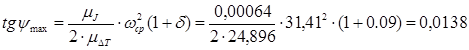

 ; ;
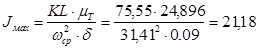 кг*м2 кг*м2
Т.к. маховик выполнен в форме стального диска, момент инерции маховика будет равен:
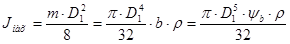 , ,
где m – масса маховика, r – плотность (для стали r=7800 кг/м3), y
b
= b/D – относительная ширина маховика.
Подставив значения получим:


Масса маховика
 (кг) (кг)
1.13 Определение истинной угловой скорости звена приведения
Истинная угловая скорость звена приведения находится следующим образом:
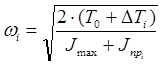 ; ;
где 
 Дж Дж
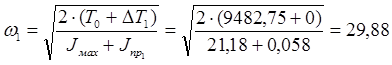 с-1 с-1
Результаты вычислений приведены в таблице 1.8
Таблица 1.8
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
 ,с-1 ,с-1
|
29,88 |
29,89 |
29,89 |
29,91 |
29,94 |
29,97 |
29,99 |
29,99 |
29,96 |
29,92 |
29,88 |
29,87 |

Проверка: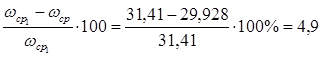 % %
2. Динамический анализ рычажного механизма
Силовой расчет механизма
Задачей силового анализа является определение при заданном законе движения неизвестной внутренней силы, то есть усилия (реакции) в кинематических парах. Эта задача решается с применением принципа Даламбера. Силовой расчет плоских рычажных механизмов выполняется по группам Асура в порядке обратном их присоединения к входному звену.
2.1 Определение углового ускорения звена приведения
Угловое ускорение определяем из дифференциального уравнения машинного агрегата:
 ; ;
где 
Расчет производим для 10-го положения механизма (Мпр
10
- максимальный).

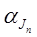 -угол наклона касательной к кривой графика -угол наклона касательной к кривой графика 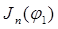 к оси абсцисс в исследуемой точке. к оси абсцисс в исследуемой точке.
Подставляем ранее определенные значения и получим:

Ведущее звено движется замедленно.
2.2 Определение линейных и угловых скоростей, ускорений точек и звеньев механизма
Для построения плана механизма в 10-ом положении примем масштабный коэффициент 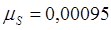 м/мм м/мм
Для построения плана скоростей определим скорость точки В.
 м/с м/с
Приняв отрезок pb=340 мм, определим масштабный коэффициент.
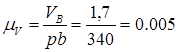 м/(с·мм) м/(с·мм)
Построение плана ведется в соответствии с векторными уравнениями рассмотренными в положении №10. Тогда действительные скорости:
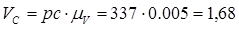 м/c м/c
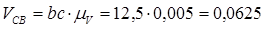 м/c м/c
 с-1 с-1
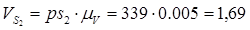 м/c м/c
Направление 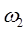 получим, поместив вектор получим, поместив вектор 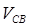 в точку С звена 2 и рассмотрев поворот звена под его действием относительно точки В. в точку С звена 2 и рассмотрев поворот звена под его действием относительно точки В.
Так как кривошип вращается неравномерно, ускорение точки В кривошипа равно:
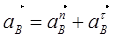


Выбираем масштабный коэффициент для ускорения 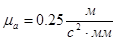 . .
Вычисляем отрезки изображающие 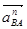 и и 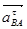
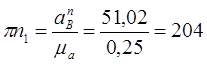 мм, мм,
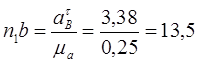 мм мм
Из полюса 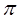 откладываем откладываем  ║ АВ направленный к центру вращения, отрезок ║ АВ направленный к центру вращения, отрезок 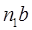 ┴ АВ в направлении ┴ АВ в направлении  . .
Ускорение точки С найдем, решив графически систему векторных уравнений.
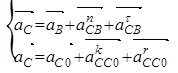
где нормальная составляющая  ║ СВ и равна: ║ СВ и равна:
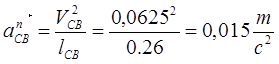
 мм мм
тангенциальная составляющая 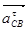 ┴ СВ. ┴ СВ.
Точка 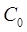 принадлежит стойке, поэтому принадлежит стойке, поэтому 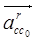 ║. ║.
Положение точки 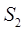 найдем по теореме подобия: найдем по теореме подобия:
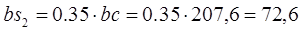 мм мм
Тогда действительные ускорения точек и звеньев равны:
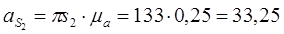 м/с2 м/с2
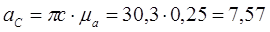 м/с2 м/с2
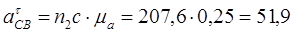 м/с2 м/с2
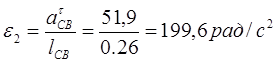
Направление 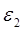 получим, помещая получим, помещая 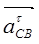 в точку С и рассматривая поворот звена 2 под его действием относительно точки В. Звено движется ускоренно. в точку С и рассматривая поворот звена 2 под его действием относительно точки В. Звено движется ускоренно.
2.3 Расчет сил, действующих на звенья механизма
Определим силы тяжести звеньев, главные векторы и главные моменты сил инерции звеньев.
Звено 1: 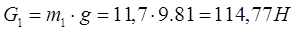
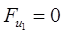 - т.к. кривошип уравновешен. - т.к. кривошип уравновешен.
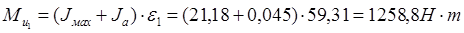
Звено 2: 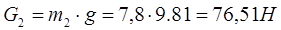
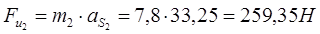
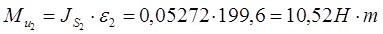
Звено 3: 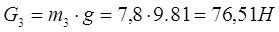

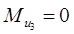
Ф2
=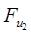 ; Ф3
= ; Ф3
=
2.4 Определение значений динамических реакций в кинематических парах групп Ассура
Fc
[10]
= 33221,2 H
Отсоединим группу Асура (2; 3). Приложим все известные внешние силы, главный вектор сил инерции Fи2
и главный момент сил инерции Ми2
, а вместо отброшенных звеньев 1 и стойки 0 приложим реакции F21
и F30
, причем неизвестного по величине F21
представим как сумму: 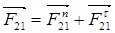 , а реакцию F30
направим перпендикулярно направляющей ползуна. , а реакцию F30
направим перпендикулярно направляющей ползуна.
Определим реакцию 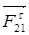 из условия из условия 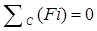 для звена 2 для звена 2

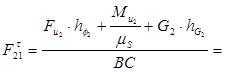 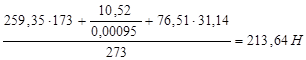
Для определения составляющей 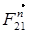 и реакции F30
запишем на основании принципа Даламбера векторное уравнение статики для групп Ассура (2; 3) и реакции F30
запишем на основании принципа Даламбера векторное уравнение статики для групп Ассура (2; 3)

Выбираем масштабный коэффициент 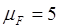 Н/мм Н/мм
Определим чертежные отрезки, изображающие силы на чертеже:
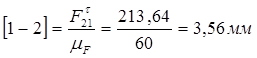
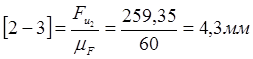
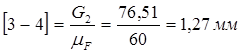
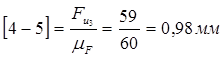
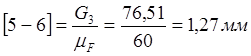
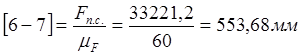
Строим план сил группы Асура (2; 3)
Из плана определяем:
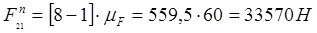
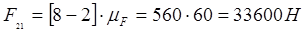

Переходим к силовому расчету механизма 1 класса. В точку В приложим реакцию  . К звену 1 прикладываем главный момент сил инерции . К звену 1 прикладываем главный момент сил инерции 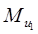 и движущий момент. Рассмотрим равновесие звена 1 относительно точки А. и движущий момент. Рассмотрим равновесие звена 1 относительно точки А.

Из плана сил определяем: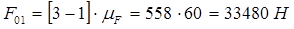 . .
2.5 Оценка точности расчетов
Находим относительную погрешность:
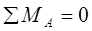
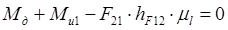
594,6 + 1258,8 – 33600·58,05·0,00095 = 1853,4 – 1852,9 = 0,5 ≈ 0.
3. Синтез зубчатого механизма
Исходные данные:
Параметры планетарного редуктора:
U1H
= 5,5; k = 4; m1
= 7 мм.
Параметры открытой зубчатой передачи:
Z4
= 15; Z5
= 28; m = 12 мм.
Параметры исходного контура по ГОСТ 16532–70:
a = 20 град; ha
*
= 1; c*
= 0,25.
3.1 Подбор чисел зубьев
Подбор чисел зубьев и числа сателлитов производим с учетом условия соосности: воспользуемся формулой Виллиса с учетом воспользуемся формулой Виллиса с учетом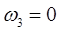
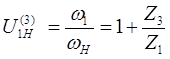 ; ; 
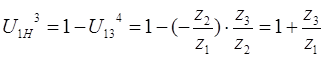 ; ; 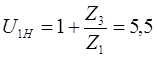
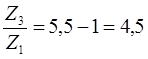
Подбор зубьев производим путем подбора с учетом ряда ограничений:
Для колес с внешними зубьями: Z1
≥ Zmin
= 17
Для колес с внутренними зубьями: Z3
≥ Zmin
= 85 при h
a
* = 1
Принимаем Z1
= 24, Z3
= (U1
H
– 1)*Z1
= 4.5 * 24 = 108
Число зубьев Z2
определяем из условия соседства:
Z1
+ Z2
= Z3
– Z2
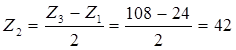 - условие целостности выполняется. - условие целостности выполняется.
Сборка нескольких сателлитов должна выполняться без натягов при равных окружных шагах между ними. Оно выражается следующим соотношением:
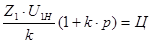 , где Ц
= 1, 2, 3, … – целое число; p
= 0 , где Ц
= 1, 2, 3, … – целое число; p
= 0
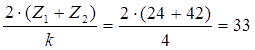 - условие целостности выполняется - условие целостности выполняется
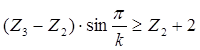 ; ; 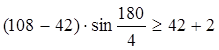
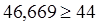 - выполняется. - выполняется.
Окончательно принимаем Z
1
= 24;
Z
2
= 42;
Z
3
= 108.
Определяем диаметры колес планетарного редуктора. Редуктор собирается из колес без смещения.
 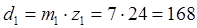 мм мм
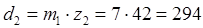 мм мм
 мм мм
Вычерчиваем схему редуктора в масштабе 1: 3
3.2 Проектирование цилиндрической эвольвенты зубчатой передачи внешнего зацепления
Исходные данные:
Z1
=13, Z2
=28 – числа зубьев колёс;
m = 8 мм – модуль зацепления;
h*
a
= 1 – коэффициент высоты головки зуба;
с*
= 0,25 – коэффициент радиального зазора.
3.2.1
Выбор коэффициентов смещения
x
1
и x
2
исходного контура
Коэффициенты смещения 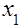 и и 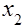 должны соответствовать условию: (При отсутствии подрезания зубьев.) должны соответствовать условию: (При отсутствии подрезания зубьев.)
x
1
³x
min
1
; x
2
³x
min
2
x
min
1
и x
min
2
определяем по формуле:
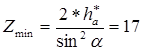 ;
;
Наименьший коэффициент смещения по критерию отсутствия подрезания зуба при заданных числах зубьев:
 ; ;
 ; ;
Выбираем коэффициенты смещения 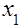 и и 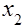 из таблицы коэффициента смещения для силовых передач при свободном выборе межосевого расстояния (Z1
= 10…30, Z2
≤ 30): x
1
=0.3; x
2
=0; x
å
=x
1
+x
2
=0,3. из таблицы коэффициента смещения для силовых передач при свободном выборе межосевого расстояния (Z1
= 10…30, Z2
≤ 30): x
1
=0.3; x
2
=0; x
å
=x
1
+x
2
=0,3.
3.2.2 Угол зацепления 
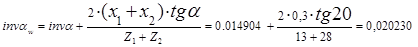 ; ;
aw
=22.06160
=220
4’
3.2.3 Делительные диаметры d
1
иd
2
d1
= m*z1
= 8*13 = 104 мм
d2
= m*z2
= 18*28 = 224 мм
3.2.8 Радиусы основных окружностей
 ; ;
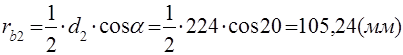 . .
3.2.4 Делительное межосевое расстояние передачи

3.2.5 Межосевое расстояние передачи
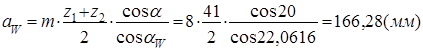
3.2.6 Коэффициент воспринимаемого смещения

3.2.7 Коэффициент уравнительного смещения

3.2.8
Радиусы начальных окружностей

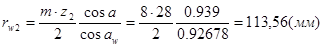
Проверка вычислений:
aw
= rw
1
+ rw
2
= 52.72 + 113.56 = 166.28 (мм)
Радиусы вершин зубьев
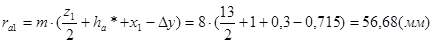
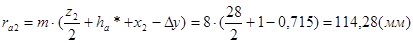
3.2.9
Радиусы впадин
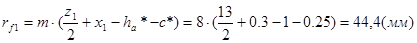

Высота зубьев колес
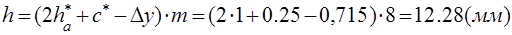
h = ra1
– rf1
= ra2
– rf2
= 56,68 – 44,4 = 114,28 – 102 = 12,28 (мм)
Основной делительный шаг зубьев
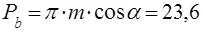 мм мм
Относительные толщины зубьев на вершинах в пределах нормы.
Вычерчиваем по полученным данным эвольвенту зубчатого зацепления в масштабе М 2,5: 1.
4. Синтез кулачкового механизма
4.1 Основные положения и определения
Кулачковым механизмом называется трехзвенный механизм, составленный из стойки и двух подвижных звеньев (кулачка и толкателя), связанных между собой посредством высшей кинематической пары. Механизм служит для воспроизведения заданного периодического закона движения ведомого звена. Ведущим звеном в кулачковом механизме является, как правило, кулачок, ведомым звеном толкатель.
Толкатель в кулачковом механизме заканчивается, как правило, вращающимся роликом, который касается кулачка непосредственно. Наличие ролика никак не отражается на законе движения толкателя. Назначение ролика – перевод трения скольжения толкателя по кулачку, в трение качения ролика по поверхности кулачка. В итоге получаем повышение долговечности кулачкового механизма по износу.
Кулачку в кулачковом механизме присущи два профиля – действительный (рабочий) и теоретический.
Действительным профилем является профиль кулачка, с которым непосредственно соприкасается ролик толкателя.
Теоретический профиль – это кривая, которую описывает центр ролика толкателя при движении относительно кулачка.
Действительный и теоретический профили кулачка являются эквидистантными (равноудаленными друг от друга) кривыми.
В движении кулачкового механизма различают в общем случае четыре этапа (фазы):
1 этап – удаление толкателя, фазовый угол  , 2 этап – дальнее стояние толкателя, фазовый угол , 2 этап – дальнее стояние толкателя, фазовый угол  . Профиль кулачка на этапе дальнего стояния есть окружность радиуса . Профиль кулачка на этапе дальнего стояния есть окружность радиуса 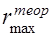 с центром на оси О вращения кулачка. с центром на оси О вращения кулачка.
3 этап – приближение толкателя, фазовый угол  . 4 этап – ближнее стояние толкателя, фазовый угол . 4 этап – ближнее стояние толкателя, фазовый угол 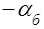 . .
Профиль кулачка на этапе ближнего стояния толкателя, является дугой окружности радиуса 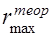 , с центром на оси О вращения кулачка. При этом , с центром на оси О вращения кулачка. При этом 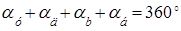 . .
Соответствие между фазовыми углами в движении кулачка и перемещением толкателя устанавливается, так называемой, циклограммой работы кулачкового механизма.
4.2 Исходные данные
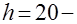 ход толкателя, мм; ход толкателя, мм;
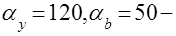 фазовые углы кулачка, соответствующие этапам удаления и приближения толкателя, градусы; фазовые углы кулачка, соответствующие этапам удаления и приближения толкателя, градусы;
 фазовые углы кулачка, соответствующие дальнему и ближнему стоянию толкателя, градусы; фазовые углы кулачка, соответствующие дальнему и ближнему стоянию толкателя, градусы;
Законы движения:
– при удалении: трапецеидальный
– при приближении: параболический симметричный
4.3 Расчет передаточных функций выходного звена
Рассчитаем перемещения Si
и аналог ускорения Si
¢ по соответствующим заданному закону формулам.
Фаза удаления:
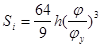 , при , при 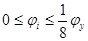
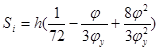 , при , при 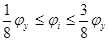
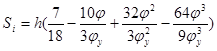 , при , при 
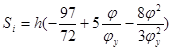 , при , при 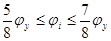
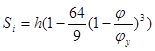 , при , при 
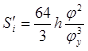 , при , при 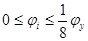
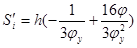 , при , при 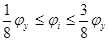
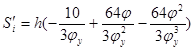 , при , при 
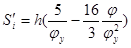 , при , при 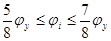
 , при , при 
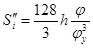 , при , при 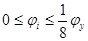
 , при , при 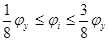
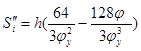 , при , при 
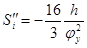 , при , при 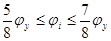
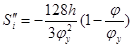 , при , при 
h = 20 (мм); φ
y
= 120º = 2.093 рад; ji
=0, 0.348, 0.697, 1.046, 1.395, 1.744, 2.093 рад
Фаза возвращения:
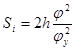 , при , при 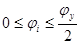
 , при , при 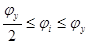
 , при , при 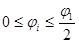
 , при , при 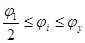
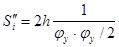 , при , при 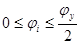
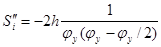 , при , при 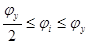
φ
b
= 50º = 0,872 рад, ji
=0, 0.145, 0.29, 0.436, 0.581, 0.726, 0.872 рад
Табл. 4.1
| i
|
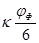 |
ji
|
Si
, м |
S`, м |
S``, м |
yi
, мм |
y`, мм |
y``, мм |
| Фаза удаления |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
20 |
20 |
0,00065 |
0,00563 |
0,03238 |
1,3 |
11,26 |
64,76 |
| 2 |
40 |
40 |
0,00395 |
0,01377 |
0,02435 |
7,9 |
27,54 |
48,7 |
| 3 |
60 |
60 |
0,01001 |
0,01908 |
0,00006 |
20,02 |
38,16 |
0,12 |
| 4 |
80 |
80 |
0,01601 |
0,01381 |
-0,0243 |
32,02 |
27,62 |
-48,6 |
| 5 |
100 |
100 |
0,01935 |
0,00531 |
-0,0243 |
38,7 |
10,62 |
-48,6 |
| 6 |
120 |
120 |
0,02 |
0 |
0 |
40 |
0 |
0 |
| Фаза приближения |
| 7 |
0 |
220 |
0 |
0 |
0,0526 |
0 |
0 |
105,2 |
| 8 |
8.33 |
228.33 |
0,0011 |
0,0133 |
0,0526 |
2,2 |
7,3 |
105,2 |
| 9 |
16.66 |
236.66 |
0,00424 |
0,0266 |
0,0526 |
8,48 |
14,6 |
105,2 |
| 10 |
24.99 |
244.99 |
0,01 |
0,04 |
0,0526 |
20 |
21,9 |
105,2 |
| 11 |
33.32 |
253.32 |
0,01554 |
0,01755 |
-0,0526 |
31,08 |
19 |
-105,2 |
| 12 |
41.65 |
261.65 |
0,01887 |
0,0088 |
-0,0526 |
37,74 |
9,5 |
-105,2 |
| 13 |
50 |
270 |
0,02 |
0 |
-0,0526 |
40 |
0 |
-105,2 |
μ
l
=
0,0005 м/мм.
4.4 Определение основных размеров
Определим минимальный радиус кулачка из условия выпуклости профиля. Для этого на основании графиков S(φ) и S» (φ), строим график S(S’’). Проведем касательную под углом 45 к оси S. За центр вращения кулачка выбираем точку Оi
лежащая ниже точки О на 10 мм.
Ro
= 0,0752 м
Проводим окружность радиусом Ro
. Так как e = 0, линия движения толкателя yy проходит через центр вращения кулачка Оi
. Вдоль этой линии от точки АО
откладывается перемещение толкателя согласно графику.
Заключение
В результате выполнения курсовой работы закрепил и обобщил знания и навыки, полученные при изучении дисциплины, научился применять на практике теорию курса (кинематику, динамику, синтез эвольвентного зацепления и синтез кулачкового механизма).
Выполняя курсовой проект по теории машин и механизмов, овладел навыками использования общих методов проектирования и исследования механизмов. Также овладел методами определения кинематических параметров механизмов, оценки сил, что действуют на отдельные звенья механизма, научился оценивать сконструированный механизм с точки зрения его назначения – обеспечивать необходимые параметры движения.
Список использованных источников
1. Попов С.А. Курсовое проектирование по теории механизмов и механике машин. – М.: Высшая школа, 1986.
2. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. – М.: Высшая школа, 1999.
3. Курсовое проектирование по теории механизмов и машин. / Под ред. Девойно Г.Н. – Мин.: Высшая школа, 1986.
4. Теория механизмов и машин. / Под ред. Фролова К.В.
|

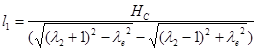
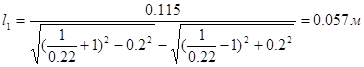 ;
; 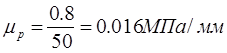 .
.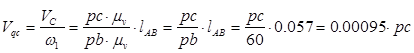
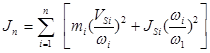

 ;
; ;
;


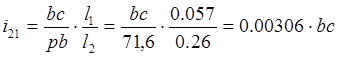
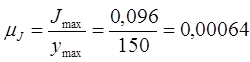 кг*м2
/мм
кг*м2
/мм
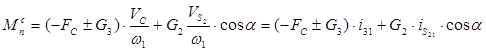
 ,то график
,то график  Дж/мм
Дж/мм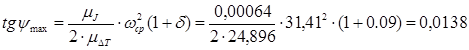


 (кг)
(кг)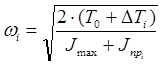 ;
; 
 Дж
Дж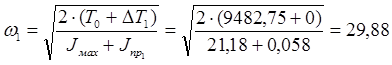 с-1
с-1

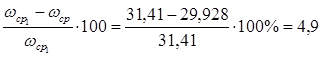 %
%
 ;
;


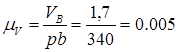 м/(с·мм)
м/(с·мм)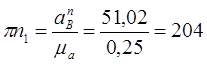 мм,
мм,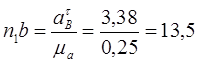 мм
мм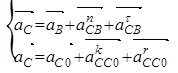
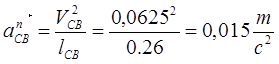
 мм
мм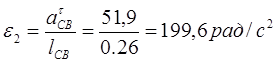

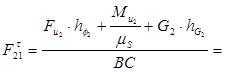
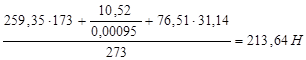
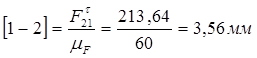
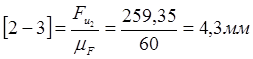
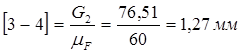
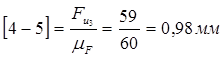
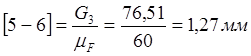
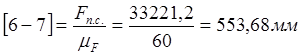
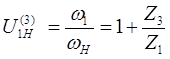 ;
; 
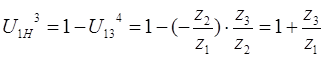 ;
; 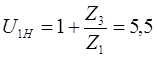
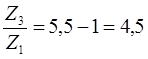
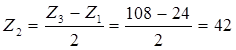 - условие целостности выполняется.
- условие целостности выполняется.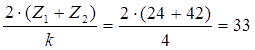 - условие целостности выполняется
- условие целостности выполняется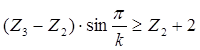 ;
; 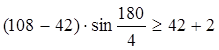
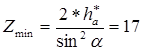 ;
; ;
;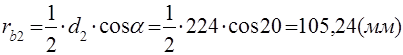 .
.
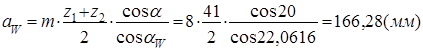
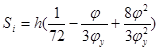 , при
, при 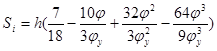 , при
, при 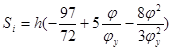 , при
, при 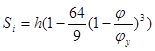 , при
, при 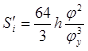 , при
, при 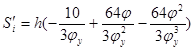 , при
, при 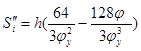 , при
, при 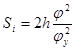 , при
, при