Министерство образования и науки Российской Федерации
РГРТА
Кафедра РТС
Пояснительная записка к курсовой работе по дисциплине
"Антенны и устройства СВЧ"
на тему:
"Зеркальная антенна РЛС"
Рязань 2004
Содержание
1. Введение
2. Расчёт геометрических параметров зеркала и облучателя
2.1 Основные параметры усечённого параболоида
2.2 Основные размеры зеркала
2.3 Основные размеры рупора
3. Расчёт основных электрических параметров и уточнение геометрических
3.1 Расчёт диаграммы направленности рупора
3.2 Аппроксимация диаграммы направленности рупора
3.3 Расчёт распределения амплитуды поля на излучающей поверхности зеркала
3.4 Аппроксимация распределения амплитуды поля на излучающей поверхности зеркала
3.5 Диаграмма направленности зеркальной антенны
3.6 Расчёт КНД зеркальной антенны
4. Конструктивный расчёт
4.1 Расчёт профиля зеркала
4.2 Облегчение конструкции зеркала
4.3 Расчёт допуска на точность установки облучателя в фокусе
4.4 Расчет допусков на точность изготовления зеркала
4.5 Описание конструкции
5. Заключение
Список литературы
Приложение
Зеркальные антенны являются наиболее широко распространенным типом антенн в дециметровом и особенно в сантиметровом диапазонах волн. Такое широкое применение зеркальных антенн объясняется относительной простотой их конструкции, возможностью получения диаграммы направленности (ДН) почти любого типа из применяемых на практике, высоким КПД, малой шумовой температурой и т.д. Зеркальные антенны легко позволяют получить равносигнальную зону, а некоторые их типы могут применяться для быстрого перемещения (качания) ДН в пространстве без заметных искажений её формы в значительном секторе углов.
Зеркальные антенны являются наиболее распространённым типом антенн, используемых для радиотелескопов и антенн с очень большой направленностью, применяемых для целей космической связи.
Широко используются зеркала с параболической формой поверхности (параболоид вращения, усечённый параболоид вращения, параболический цилиндр.), также распространены сферические зеркальные антенны, двухзеркальные антенны.
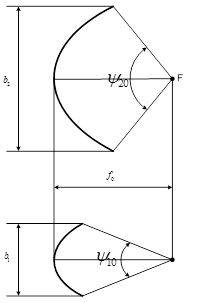
 - фокус; - фокус;  - фокусное расстояние; - фокусное расстояние;  - размер раскрыва в вертикальной плоскости; - размер раскрыва в вертикальной плоскости; 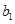 - размер раскрыва в горизонтальной плоскости; - размер раскрыва в горизонтальной плоскости; 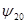 - угол раскрыва (апертурный угол) в вертикальной плоскости; - угол раскрыва (апертурный угол) в вертикальной плоскости; 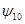 - угол раскрыва (апертурный угол) в горизонтальной плоскости. - угол раскрыва (апертурный угол) в горизонтальной плоскости.
Основные размеры зеркала определим из выражения для коэффициента направленного действия (КНД) 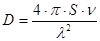 [1], где [1], где 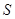 - площадь раскрыва зеркала; - площадь раскрыва зеркала; 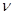 - коэффициент использования поверхности; - коэффициент использования поверхности; 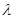 - рабочая длина волны антенны. КНД равен заданному коэффициенту усиления - рабочая длина волны антенны. КНД равен заданному коэффициенту усиления 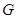 , если принять КПД антенны , если принять КПД антенны 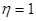 , т.к. , т.к.  , , 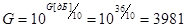 . .
Для передающей зеркальной антенны необходимо обеспечить такое облучение, чтобы ослабление поля на краях по всему контуру зеркала было одинаково и составляло 10-14 дБ относительно его центра. С учётом этого условия определяем коэффициент использования поверхности по таблице приведенной в [2]: 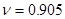 . Вводим поправку 25% (5% на тень и 20% на перелив энергии через края зеркала) и получаем . Вводим поправку 25% (5% на тень и 20% на перелив энергии через края зеркала) и получаем 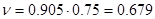 . .
Теперь можно определить площадь раскрыва:
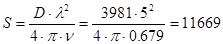 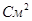 . .
Так как по заданию 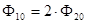 , то примем , то примем 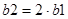 и получим следующие значения и получим следующие значения
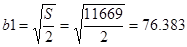  , , 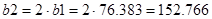  . .
Зададимся углом раскрыва зеркала в вертикальной плоскости 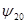 . Для передающих антенн апертурный угол лежит в пределах . Для передающих антенн апертурный угол лежит в пределах 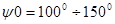 . [1] Возьмём . [1] Возьмём 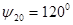 . По углу . По углу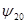 определяем фокусное расстояние зеркала: определяем фокусное расстояние зеркала: 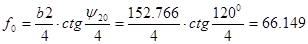  , по которому определяем угол раскрыва в горизонтальной плоскости , по которому определяем угол раскрыва в горизонтальной плоскости
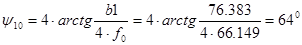 . .
Так как на краях зеркала должно быть обеспечено ослабление поля 10 дБ, то ширина нормированной диаграммы направленности облучателя по мощности на уровне 0,1 (по напряжённости на уровне 0,3) должна быть равной углу раскрыва зеркала.
В качестве облучателя возьмем пирамидальный рупорный облучатель, возбуждаемый прямоугольным волноводом.
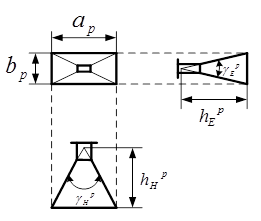
Размеры раскрыва рупора выберем по требуемой диаграмме направленности в соответствующей плоскости. Ширина диаграммы направленности связана с размерами раскрыва  и и 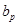 следующими соотношениями: следующими соотношениями:
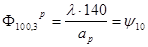 , , 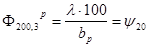 , откуда получаем , откуда получаем
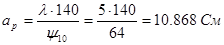 , , 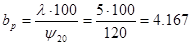  , ,
где 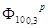 - ширина нормированной диаграммы направленности рупора по напряжённости на уровне 0,3 в плоскости Н, - ширина нормированной диаграммы направленности рупора по напряжённости на уровне 0,3 в плоскости Н, 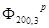 - ширина нормированной диаграммы направленности рупора по напряжённости на уровне 0,3 в плоскости Е. Рассчитаем высоты рупора в плоскости Е и в плоскости Н: - ширина нормированной диаграммы направленности рупора по напряжённости на уровне 0,3 в плоскости Е. Рассчитаем высоты рупора в плоскости Е и в плоскости Н:
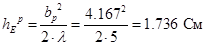 , , 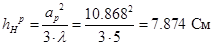
Выберем стандартный волновод по заданной длине волны 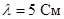 из таблицы приведённой в [4]. Возьмём волновод R-70 с размерами из таблицы приведённой в [4]. Возьмём волновод R-70 с размерами 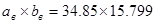 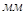 и предельной мощностью и предельной мощностью 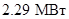 . .
Пересчитаем по уравнению стыковки высоту рупора в плоскости Е
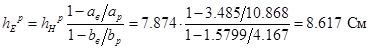 [2]. [2].
Углы раскрыва рупора в плоскости Е и в плоскости Н:
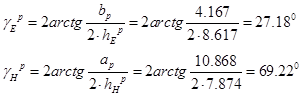
Нормированная диаграмма направленности рупора в плоскости Е:
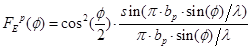
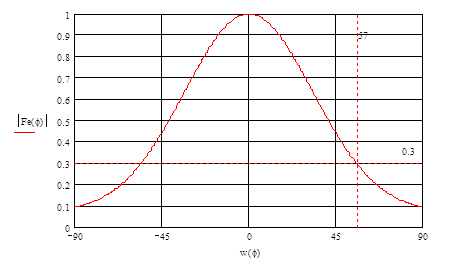
Нормированная диаграмма направленности рупора в плоскости Н:
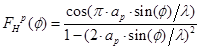
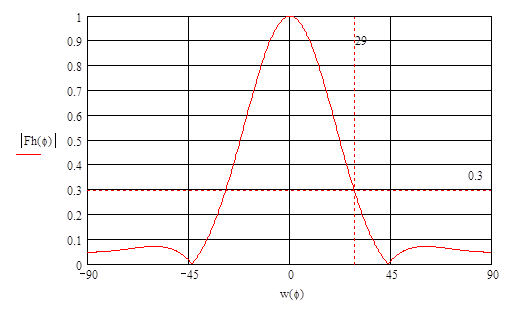
Аппроксимируем диаграмму направленности рупора в плоскости Е в пределах главного лепестка функцией 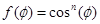 и для полученного значения и для полученного значения 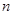 определим максимальный коэффициент использования поверхности зеркала определим максимальный коэффициент использования поверхности зеркала 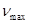 и соответствующий ему оптимальный угол раскрыва зеркала в вертикальной плоскости и соответствующий ему оптимальный угол раскрыва зеркала в вертикальной плоскости 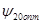 . .
Диаграмма направленности достаточно хорошо аппроксимируется функцией 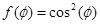 т.е. т.е. 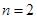 . .
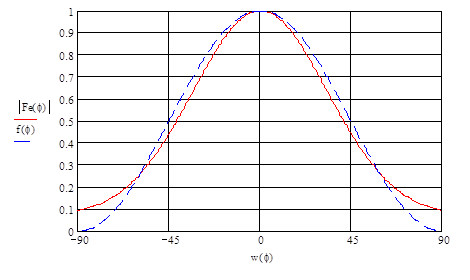
Значения 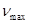 и и 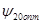 определяем по зависимости определяем по зависимости
 при при  . .
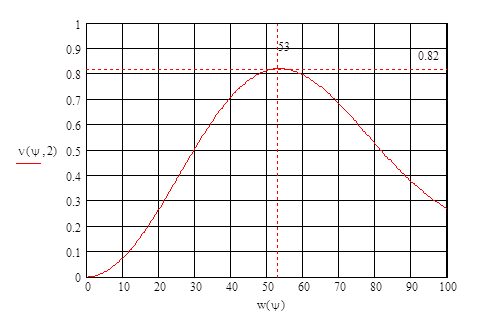
Таким образом  а а 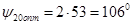 . .
Пересчитываем фокусное расстояние для оптимального угла раскрыва
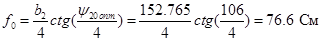 . .
Уточняем фокусное расстояние по синфазности излучения облучателя назад с основным излучением антенны. Для обеспечения синфазности излучения должно выполняться условие 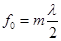 , где , где 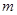 -целое число. [4] -целое число. [4]
 ; ; 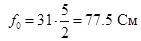 . .
Нормированное распределение амплитуды поля в вертикальной плоскости описывается выражением 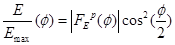 . Для перехода к зависимости . Для перехода к зависимости 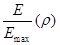 , , 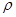 - координата точки по раскрыву зеркала, воспользуемся выражением из геометрической оптики - координата точки по раскрыву зеркала, воспользуемся выражением из геометрической оптики  и получим следующее выражение: и получим следующее выражение:
 , ,
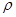 изменяется от изменяется от  до до  . .
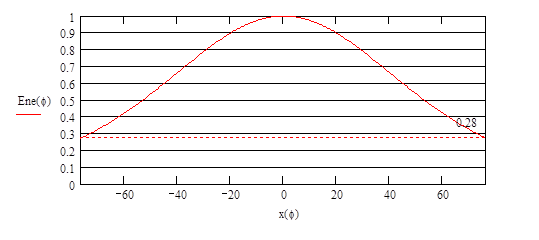
Нормированное распределение амплитуды поля в горизонтальной плоскости описывается выражением 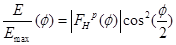 или в зависимости от координаты по раскрыву зеркала или в зависимости от координаты по раскрыву зеркала
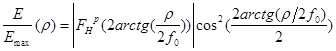 , ,
где 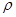 изменяется от изменяется от 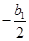 до до 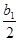 . .
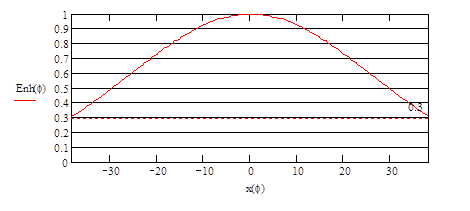
Так как амплитуда поля на краях раскрыва зеркала отлична от нуля, то
В этом случае удобна аппроксимация 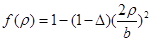 . [1] . [1]
В вертикальной плоскости  , где , где  , , 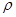 изменяется от изменяется от  до до  . .

В горизонтальной плоскости
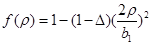 , ,
где 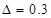 , , 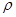 изменяется от изменяется от 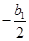 до до 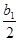 . .
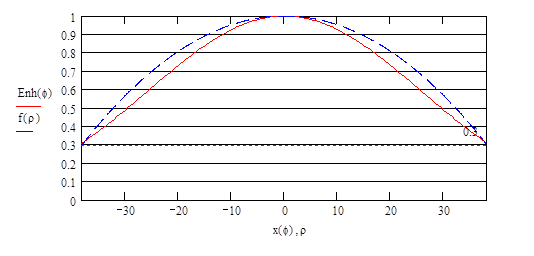
Ненормированная диаграмма направленности зеркальной антенны без учёта тени от облучателя определяется выражением 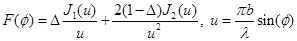 [2]. Ненормированная диаграмма направленности зеркальной антенны в вертикальной плоскости: [2]. Ненормированная диаграмма направленности зеркальной антенны в вертикальной плоскости: 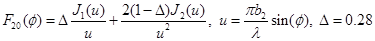 . Нормированная диаграмма направленности: . Нормированная диаграмма направленности: 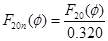 . Ненормированная диаграмма направленности зеркальной антенны в горизонтальной плоскости: . Ненормированная диаграмма направленности зеркальной антенны в горизонтальной плоскости:  . Нормированная диаграмма направленности: . Нормированная диаграмма направленности:  . .

Нормированная диаграмма направленности с учётом тени от облучателя: в вертикальной плоскости 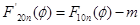 , где , где 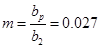 ; в горизонтальной плоскости ; в горизонтальной плоскости 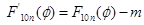 , где , где 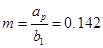 . .
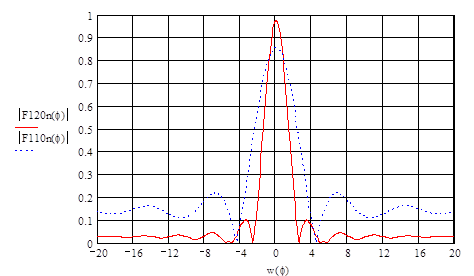
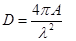 , ,  - действующая площадь антенны, - действующая площадь антенны, 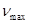 - максимальный коэффициент использования поверхности зеркала, - максимальный коэффициент использования поверхности зеркала, 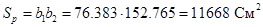 - геометрическая площадь раскрыва зеркала, - геометрическая площадь раскрыва зеркала, 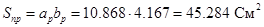 - площадь облучателя, закрывающего раскрыв спереди. [4] - площадь облучателя, закрывающего раскрыв спереди. [4]
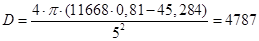
Зеркало представляет собой усечённый параболоид вращения. Так как нужно обеспечить одинаковое (10-14 дБ) ослабление поля на краях по всему контуру зеркала, то его нужно обрезать не по прямой линии, а по некоторой кривой, являющейся контуром равной интенсивности поля.
Диаграмма прямоугольного рупора на заданном уровне (10 дБ) имеет сечение, близкое к эллиптическому. Такую же эллиптическую форму должен иметь контур зеркала. [3]
Уравнение поверхности зеркала в декартовой системе координат имеет следующий вид: 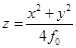 . .
Сечение зеркала вертикальной плоскостью имеет вид:

Сечение зеркала горизонтальной плоскостью имеет вид:
С целью уменьшения веса и парусности параболических антенн их отражатели выполняют из решёток или перфорируют. Решётчатая поверхность выполняется из металлических проводов или пластин. Расстояния между элементами решётки должны быть меньше половины длины волны, вектор электрического поля, излучаемого облучателем, должен быть параллельным элементам решётки.
Зеркало можно считать хорошим, если коэффициент прохождения не превышает 1%. Коэффициент прохождения определяется как отношение энергии волны, прошедшей за зеркало, к энергии падающей волны.
Коэффициент прохождения для параболоида вращения можно рассчитать по следующей приближённой формуле:  , где , где 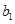 - наименьший размер раскрыва; - наименьший размер раскрыва; 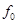 - фокусное расстояние; - фокусное расстояние; 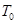 - коэффициент прохождения для плоской поверхности той же конструкции, что и рассматриваемое зеркало; - коэффициент прохождения для плоской поверхности той же конструкции, что и рассматриваемое зеркало; 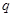 - коэффициент неравномерности поля. - коэффициент неравномерности поля.
Рассчитаем основные параметры для решётки, выполненной из металлических проводов. Зависимость коэффициента 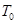 от относительного расстояния между осями соседних проводов от относительного расстояния между осями соседних проводов 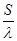 для бесконечной плоской решётки приведена в [2]. Зададимся значением для бесконечной плоской решётки приведена в [2]. Зададимся значением 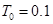 и значением и значением 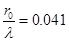 , , 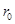 -радиус провода. По этим значениям получим -радиус провода. По этим значениям получим 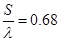 . Коэффициент . Коэффициент 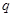 можно приближённо считать равным коэффициенту использования поверхности зеркала можно приближённо считать равным коэффициенту использования поверхности зеркала 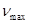 [4], тогда [4], тогда 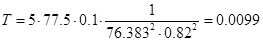 или или 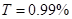 . Радиус провода . Радиус провода 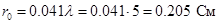 , расстояние между осями соседних проводов , расстояние между осями соседних проводов  . .
Для получения в раскрыве параболической антенны волны с плоским фазовым фронтом необходимо фазовый центр облучателя помещать по возможности точнее в фокусе параболической поверхности. Определим, с какой точностью необходимо выполнять это условие. Допустимый сдвиг облучателя из фокуса определяется неравенством
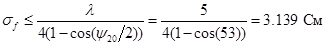 . [4] . [4]
При определении допуска на точность изготовления зеркала исходят из допустимой фазовой ошибки в раскрыве, равной 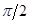 . Это даёт: . Это даёт: 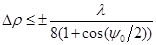 , где , где 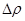 -допустимое отклонение радиуса вектора поверхности зеркала. Допуск в центральной части зеркала равен, таким образом, -допустимое отклонение радиуса вектора поверхности зеркала. Допуск в центральной части зеркала равен, таким образом, 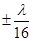 , а на периферии зеркала может быть менее жёстким. [2] , а на периферии зеркала может быть менее жёстким. [2]
Допуск в центральной части зеркала 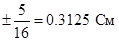 ; допуск для большего угла раскрыва ; допуск для большего угла раскрыва 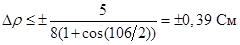 ; допуск для меньшего угла раскрыва ; допуск для меньшего угла раскрыва 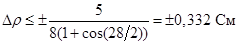 . .
Полученная зеркальная антенна состоит из следующих частей (см. приложение):
1) рефлектор (зеркало), представляющий собой усечённый параболоид вращения, и выполненный из тонких металлических проводов;
2) облучатель - пирамидальный рупор, обеспечивающий вертикальную поляризацию;
3) опоры рефлектора;
4) механизм вращения по азимуту;
5) подзеркальник;
6) механизм вращения по углу места;
7) питающий волновод;
8) оббортовка;
9) опоры облучателя;
10) платформа антенны.
В результате выполнения работы была разработана зеркальная антенна, удовлетворяющая заданным техническим требованиям: обеспечена веерная диаграмма направленности (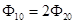 ); работа осуществляется на длине волны ); работа осуществляется на длине волны 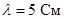 ; обеспечена линейная поляризация (вертикальная); предусмотрена защита от ветровой нагрузки. ; обеспечена линейная поляризация (вертикальная); предусмотрена защита от ветровой нагрузки.
1. Власов В.И., Берман Я.И. "Проектирование высокочастотных устройств радиолокационных станций". Ленинград, издательство "Судостроение". Ленинград, 1972.
2. Жук М.С., Молочков Ю.Б. "Проектирование антенно-фидерных устройств". М. -Л., издательство "Энергия", 1966.
3. Драбкин А.Л. и др. "Антенно-фидерные устройства". Изд.2-е, дополненное и переработанное. М., "Сов. радио", 1974.
4. Дорохов А.П. "Расчёт и конструирование антенно-фидерных устройств". Издательство Харьковского университета, 1960.

|