Уявлення про симетрію дуже важливі у зв’язку, як з теоретичним, так і експериментальним вченням про будову молекул. Основні принципи симетрії використовуються у квантовій механіці, молекулярній спектроскопії та для визначення структури за допомогою дифракції нейтронів, електронів і рентгенівського випромінювання. Симетричними називаються предмети
, які при дії на них операцій симетрії здатні до самосуміщення. Встановлення симетрії молекул здійснюється за допомогою елементів симетрії. Елементи симетрії
– це уявні геометричні образи, за допомогою яких встановлюється симетрія молекул. Для опису симетрії молекул використовують п’ять типів елементів симетрії:
1) центр симетрії;
2) вісь власного обертання;
3) зеркальна площина;
4) інверсійні осі, або зеркально-поворотні осі;
5) елемент тотожності.
Кожен з цих елементів має зв’язану з ним операцію симетрії. Операція симетрії
– це дія над молекулою із метою встановлення її симетрії. Елементи і операції симетрії зв’язані між собою. Цей зв’язок приведений в табл. 1.
Таблиця 1. Елементи симетрії і зв’язані з ними операції
| Символ
|
Елемент
|
Операція
|
i(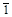 ) (C) ) (C) |
Центр симетрії |
Проекція через центр симетрії на рівну віддаль на другий бік від центру |
| Cn(n) Lh
|
Вісь власного обертання |
Поворот за годинниковою
стрілкою навколо осі на
кут 2π/n (або 360/n)
|
| σh
(n) p |
Горизонтальна зеркальна площина, перпендикуляр
на головній осі Сn
|
Відбиття в площині
симетрії
|
 , Lin , Lin
|
Інверсійна вісь |
Поворот за годинниковою
стрілкою навколо осі Сn –
на кут 360/n з наступним відбиттям в центрі симетрії перпендикулярній цій осі (тобто комбінована
операція Сn-обертання з наступним відбиттям взеркальній площині σn
|
| Sn |
Зеркально-поворотна вісь |
Поворот за годинниковою
стрілкою навколо осі на
кут 360/n з наступним від-
биттям у перпендикулярній площині
|
| Еi
(L1
)1
|
Елемент тотожності |
Відповідає повороту на 360° |
Центр симетрії і операції інверсії
. Молекула має центр симетрії
(i), якщо пряма лінія, проведена від будь-якого атома через центр молекули, перетне еквівалентний атом, розміщений на рівній віддалі від центра. Центр симетрії є елементом симетрії, а відповідна операція
– інверсія через центр
, при якій половина молекули може бути одержана з іншої половини. Дія операції інверсії полягає в перетворенні координат точки
(x, y, z) в координати (–x, – y, – z). Операції інверсії можна представити:
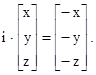
Якщо операцію інверсії провести два рази, то одержується початкова конфігурація:
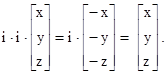
Таким чином, послідовне проведення операції (i) парну кількість раз дає операцію Е (тотожність).
Приклади центросиметричних молекул: С6
Н6
, SF6
, CO2
, C2
H4
.
Вісь симетрії і операція обертання
. Вісь симетрії
– це лінія, поворот навколо якої на кут 360/n дає структуру, що самосуміщається з вихідною. Операцію обертання
позначають символом Cn (Ln
) або n, де n– порядок обертання. Обертання за годинниковою стрілкою вважається додатнім. Якщо вісь z є вісь обертання С2
, то дія операції обертання полягає в перетворенні координат (x, y, z) в координати (–x, – y, – z). Операцію обертання С2
можна представити так:
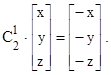
Будь-яка лінійна молекула має С¥, так як форма молекули не зміниться при повороті на будь-який кут навколо осі, що співпадає з міжядерною віссю:
¯
НС
¥
Cl
||.
СlCl
Молекула Н2
О має вісь С2
, яка проходить через атом О і ділить кут між зв’язками НО пополам (мал.).
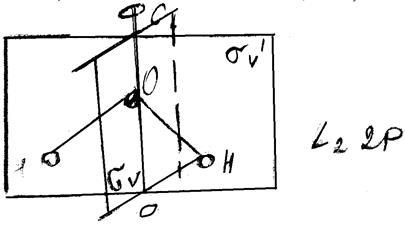
Рис. Елементи симетрії молекули Н2
О.
Молекула NH3
має вісь С3
, що проходить через атом азоту. Молекула С6
Н6
має вісь С6
перпендикулярну площині бензольного кільця.
Наявність осі симетрії може викликати декілька операцій симетрії. Операцію симетрії, що включає поворот за годинниковою стрілкою на кут 360/n і проведену послідовно kраз, позначають Сn
k
.
Операції зв’язані з віссю С2
: С2
1
, С2
2
= Е. Перша операція – поворот на 180°, а друга – поворот на 360°, який відповідає операції тотожності Е. Тоді С2
відповідає тільки одна операція С2
1
: С2
3
= С2
1
і С2
4
= Е, тобто при операції обертання (Сn
) для деяких k > n нових операцій не виникає.
Операції симетрії для осей С3
, С4
та С6
:
С3
¸ С3
1
С3
2
; С3
3
= Е.
С4
¸ С4
1
С4
2
= С2
1
; С4
3
; С4
4
= Е.
С6
¸ С6
1
С6
2
= С3
1
; С6
3
= С2
1
; С6
4
= С3
2
; С6
5
; С6
6
= Е.
Для С6
є дві операції, які не можуть бути одержані іншим методом.
При обговоренні симетрії молекули зручно визначати положення молекул в прямокутниї декартових координатах. Центр ваги молекули фіксується в початку декартових координат, а її головна вісь співпадає з віссю z. Головна вісь визначається як вісь Сn вищого порядку. Якщо у молекулі є декілька осей обертання однакового вищого порядку, то за вісь z береться вісь, яка проходить через найбільше число атомів.
Площина симетрії і операція відбиття
. Площина симетрії
– це площина, яка ділить молекулу на дві рівні частини таким чином, що частина молекули по один бік від неї є зеркальним відображенням другої частини. Символ σ – позначає як елемент, так і операцію відбиття. σk
= σ, якщо k – непарне і σk
= Е, коли k – парне.
Якщо площина xz– зеркальна площина (на ^ до осі у), то операція відбиття σ може бути зображена слідуючим чином:
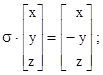
Зеркальна площина перпендикулярна Сnназивається горизонтальною зеркальною площиною
і позначається σh
. Зеркальні площини, що проходять через головну вісь Сn, називаються вертикальними зеркальними площинами
і їх позначають σv
.
Діагональні вертикальні площини, які ділять кути, утворені парою горизонтальних осей С2
на дві рівні частини позначають σd
.
Молекула Н2
О має дві вертикальні взаємноперпендикулярні діагональні зеркальні площини σv
і σv
1
. Одна з них співпадає з площиною молекули, а друга перпендикулярна до неї. Вісь С2
лежить на перетині двох зеркальних площин (мал.).
Лінійна молекула HCl має нескінченне число вертикальних зеркальних площин σv
і всі вони включають С¥
.
Зеркально-поворотна вісь – складний елемент, що складається з осі симетрії і перпендикулярної площини σh
. Операція симетрії, що відповідає цьому елементу симетрії, складається з повороту на певний кут, за яким слідує відбиття в площині перпендикулярній до осі. Позначається цей елемент Sn і є добутком двох операцій: Sn = σh
· Cn.
S1
еквівалентна σ – поворот на 360° з послідовним відбиттям в площину, перпендикулярно осі обертання і може бути представлене, як відбиття в зеркальній площині.
S2
– еквівалентна (i) – центру симетрії, оскільки операція S2
складається з повороту за годинниковою стрілкою на 180° з послідовним відбиття у зеркальній площині перпендикулярно осі дає ту ж конфігурацію, що і інверсія в центрі (точці), що знаходяться на перетині осі обертання і площини відбиття.
Теореми взаємодії елементів симетрії. Точкові групи
.
1. Якщо до осі симетрії n-го порядку єперпендикулярна вісь другого порядку, то через точку їх перетину проходить nтаких осей з кутом між ними b = 360/n (Ln
+ ^ L2
® Ln
nL2
). Звідси: наявність двох осей другого порядку
, що перетинаються під кутами
90, 60, 45, 30°спричиняє обов
’язкове існування осей
2, 3, 4 і 6 перпендикулярних до вихідних
.
2. Якщо вісь
n-го порядку лежить у площині симетрії
, то вздовж цієї осі перетинається
nтаких площин під кутом
b = 360/n (Ln
+ || Р ® Ln
nР).
3. Якщо вісь симетрії першого порядку
(2, 4, 6) перпендикулярна до площини симетрії
, то точкою їх перетину буде центр симетрії
(L2
n
+ ^ Р ® L2
n
РС).
4. Якщо площина симетрії і вісь другого порядку перетинаються під кутом
45°, то через точку їх перетину в цій площині проходить інверсійна вісь четвертого порядку
Li
4
+ ^ L2
(|| P) = Li
4
2L2
2P).
Повна сукупність елементів симетрії молекули називається точковою групою
або видом симетрії
.Для визначення точкової групи молекули можна скористатися схемою:
1. Визначають чи має молекула декілька осей Сn, де n > 2, що перетинаються. Якщо є такі осі, то молекула відноситься до точкової групи вищої симетрії
.
2. Якщо осей вказаних в пукті 1 немає, то шукають присутність одної осі вищого порядку (середня категорія
) Сn, потім починають визначати площини симетрії та центр симетрії.
3. Якщо осей вище 2-го порядку немає, то молекула належить до низької симетрії
.
Для позначення точкових груп користуються різною номенклатурою: міжнародною, формулами симетрії Браве або символами Шенфліса. В табл. 2 приведені символи точкових груп та наявні елементи симетрії в молекулах.
Таблиця 2. Типові групи по Шенфлісу і наявні елементи симетрії
| Символ
|
Елементи симетрії
|
Символ
|
Елементи симетрії
|
| С1
|
E |
D3
h
|
E, С3
(S3
),3С2
, σh
, 3σv
|
| Сs
|
E, σ |
D4
h
|
E, С4
(С2
, S4
) 4С2
, σh
, 2σv
,σd
, i |
| Сi
|
E, i |
D5
h
|
E, С5
(S5
), 5С2
, σh
, 5σv
|
| С2
|
E, C2
|
D6
h
|
E, С6
(С3
, С2
, S6
, S3
)
6С2
, σh
, 3σv
, 3σd
, i
|
| С2v
|
E, С2
, 2σv
|
D¥
h
|
E, С¥
(S¥
),¥С2
, σh
¥σv
, I (C2
H2
)
|
| С3v
|
E, С3
, 3σv
|
D2d
|
E, С2
(S4
), 2С2
, 2σd
|
| С4v
|
E, С4
, 4σv
|
D3d
|
E, С3
(S6
),3С2
, 3σd
, i |
| С¥
v
|
E, С¥
, ¥σv
|
D4d
|
E, С4
(S8
, С2
), 4С2
, 4σd
, i |
| С2n
|
E, С2
, σh
, i |
D5d
|
E, С5
(S10
), 5S3
, 5σd
, i |
| С3h
|
E, С3
, (S3
) σh
|
Td |
E, 3С2
(3S2
), 4C3
, 6σd
|
| D2h
|
E, С2
, 2С2
, σh
,
2σv
, i
|
On |
E, 3С4
(3С2
, 3S4
), 4С2
, (4S6
) 3σh
, 6C2
, 6σd
, i |
Для молекул існує будь-яка кількість точкових груп, для кристалів – 32 точкові групи.
Будь-яку молекулу можна віднести до якогось виду симетрії, які ділять на три категорії. Нижча категорія характеризує молекули без осей вищого порядку. Середня – з одною віссю вищого порядку. Вища – з кількома осями вищого порядку. Види симетрії за характерними ознаками розподіляють на сім сингоній. Сингонією називається група видів симетрії
, що має один або декілька подібних елементів симетрії при одинаковій кількості одиничних напрямків. Нижча категорія
включає три сингонії – триклінну
, моноклінну
та ромбічну
. Середня категорія
– тригональну
, тетрагональну
і гексагональну
. Вища категорія
– кубічну сингонію
.
Основи теорії груп. Зображення. Характер
. З точки зору теоретико-групового аналізу група – це множина G елементів, що задовільняє певним вимогам. Набір операцій симетрії, яким володіє будь-який об’єкт, теж утворює групу. Така група повинна задовільняти наступним вимогам:
1. Якщо А і В є операціями симетрії даної групи, то їх добуток дає третю операцію симетрії F, що також є операцією даної групи (добуток двох елементів множини є також її елементом). Якщо добуток А ´ В = В ´ А, то множення називається комутативним
, тобто порядок виконання операцій не впливає на результат.
2. Для трьох будь-яких елементів групи вірним є сполучний закон, або закон
асоціативності
: (А ´ В) ´ С = А (В ´ С).
3. Для кожного елементу множини існує обернений елемент, який належить тій чи іншій множині: А · А–1
= Е.
4. В кожній групі є операція ідентичності Е, яка відповідає повороту на 360°. В цьому випадку для будь-якої операції виконується співвідношення: А ´ Е = Е ´ А = А.
Ці чотири правила називаються груповими аксіомами
.
З метою визначення усіх симетричних перетворень об
’єкту
відповідної точкової групи симетрії користуються
так званим квадратом Кейлі
, що являє собою таблицю взаємного множення всіх пар симетричних перетворень. Операції симетрії записуються у верхньому рядку квадрата і в лівому його стовбчику. Добутки операцій записують у клітинках перетину рядів і стовбчиків таблиці. Для прикладу наведемо квадрат Кейлі для точкової групи С2
v
(mm2), (L2
2P)
Визначимо набір операцій симетрії – (4) – 1 (Е), 2z, mx
, my
.
| 1 |
2z |
mx
|
my
|
| 1z |
1 |
2z |
mx
|
my
|
| 2z |
2z |
1 |
my
|
mx
|
| mx
|
mx
|
my
|
1 |
2z |
| my
|
my
|
mx
|
2z |
1 |
Добуток будь-яких двох операцій симетрії дорівнює третій операції симетрії, що належить цій же групі.
Квадрат Кейлі для точкової 32 (L3
3L2
) – 6 операцій симетрії.
| E |
31
|
32
|
2x |
2y |
2u |
| Е |
E |
31
|
32
|
2x |
2y |
2u |
| 31
|
31
|
32
|
E |
2y |
2u |
2x |
| 32
|
32
|
E |
31
|
2u |
2x |
2y |
| 2х |
2x |
2u |
2y |
E |
32
|
31
|
| 2у |
2y |
2x |
2u |
31
|
E |
32
|
| 2u |
2u |
2y |
2x |
32
|
31
|
E |
Якщо міє елементами двох груп є взаємно-однозначна відповідність (добуток двох будь-яких елементів одної групи відповідає добутку двох елементів іншої групи, вони називаються ізоморфними
.
Всі симетричні операції групи симетрії складають її симетричне зображення
. Наприклад, в групу симетрії mmmbL2
3PCвходять 8 операцій симетрії: Е, 2х, 2у, 2z, C(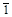 ), mx
, my
, mz
. Порядок групи 8. Вони складають симетричне зображення групи. ), mx
, my
, mz
. Порядок групи 8. Вони складають симетричне зображення групи.
У загальному вигляді зображення Г групи G подається у вигляді сукупності матриць, що відповідають всім операціям симетрії цієї групи.
Розглянемо зображення операцій симетрії точкової групи С2
v
на одиничний вектор  , направлений вздовж осі х. Точкова група С2
v
має чотири операції симетрії: Е, С2
, mx
, my
. , направлений вздовж осі х. Точкова група С2
v
має чотири операції симетрії: Е, С2
, mx
, my
.
Результати перетворення координат вектора  прийнято представляти за допомогою таблиць характерів. Якщо напрямок вектора при проведенні операцій симетрії не змінюється, то характер позначається +1, якщо змінюється, то –1. прийнято представляти за допомогою таблиць характерів. Якщо напрямок вектора при проведенні операцій симетрії не змінюється, то характер позначається +1, якщо змінюється, то –1.
1) Операція Е не змінить напрям вектора, тому характер цієї операції симетрії позначився +1.
2) 2z– поворот вектора  на 180° вздовж осі zзмінить координату вектора на 180° вздовж осі zзмінить координату вектора  на протилежну. Характер цієї операції позначається –1. на протилежну. Характер цієї операції позначається –1.
3) Операція my
(площина перпендикулярна до осі у); відбиття у цій площині не змінив напрямок вектора  ; характер операції +1. ; характер операції +1.
4) Операція mx
(площина симетрії перпендикулярна осі х); відбиття у цій площині змінить напрямок вектора  на протилежний. Характер операції симетрії –1. на протилежний. Характер операції симетрії –1.
Результати перетворення координат вектора  прийнято представляти за допомогою таблиці характерів. прийнято представляти за допомогою таблиці характерів.
Розглянемо характери операцій симетрії вектора хуzв точковій групі С2
v
.
1) Е не змінить напрямок вектора хуz. Характер операції симетрії в цьому випадку представляється як сума коефіцієнтів хуz = 1 + 1 + 1 = 3.
2) 2zкоординату х і у змінить на протилежні, а zзалишиться без зміни: –1–1+1 = –1.
3) Операції mx
: х = х, у = – у, z = z; +1–1+1 = +1.
4) Операція mу
: х = – у, у = у, z = z; –1+1+1 = +1.
| Е |
2z |
mx
|
my
|
| 1 |
–1 |
1 |
–1 |
| 1 |
–1 |
1 |
+1 |
| 1 |
+1 |
+1 |
+1 |
| 3 |
–1 |
+1 |
+1 |
Повне або приведене представлення цих операцій теж можемо представити у таблиці:
Е 2zmx
my
3 –1 +1 +1.
Приведене представлення можна розкласти на суму неприведених представлень.
Симетрія молекул і нормальні коливання
. Будь-яка молекула відноситься до певної точкової групи, тобто володіє певним набором елементів симетрії. Повна сукупність операціїй симетрії приводиться в таблицях типів симетрії і характерів представлень.
При коливаннях молекул можливі тільки певні комбінації властивостей симетрії зміщеної від рівноважної конфігурації.
Нормальні коливання називаються симетичними
(s) по відношенню до даної операції симетрії, якщо при її виконанні вектори зміщень атомів не змінюють знак і абсолютне значення (домножуються на +1).
Антисиметричне коливання
(аs) відносно операції симетрії є таким, коли при її виконанні знак зміщень змінюється на протилежний (домножується на –1).
Нормальне коливання
, яке є симетричним відносно всіх операцій симетрії даної точкової групи називається повносиметричним
.
Всі інші типи нормальних коливань неповносиметричні
: два (Е) або три (F) вироджені
.
При невироджених коливаннях операції симетрії переводять одну форму коливань в іншу, тобто вектори зміщень домножуються на числа не всі рівні 1 або всі нерівні 1.
Повна характеристика типу симетрії нормального коливання описується його відношенням до всіх операцій симетрії даної точкової групи.
Невироджені типи симетрії позначаються символами А і В. При цьому буквою А позначають коливання симетрії відносно виділеної головної осі
, орієнтованої вершиноюВ-коливання антисиметричні відносно такої осі
.
Підстрочні індекси
gі uпри А і В позначають симетричні і антисиметричні коливання по відношенню до операції інверсії в центрі (с). Підстрочні цифрові індекси 1 і 2 симетричний і антисиметричний тип коливань по відношенню до операції відбиття у вертикальній площині σv
.
Надстрочні індекси
– один штрих (¢) або два штриха (²) при буквах – позначають симетричний і антисиметричний типи коливань відносно відбиття в горизонтальній площині σh
перпендикулярної головної осі симетрії.
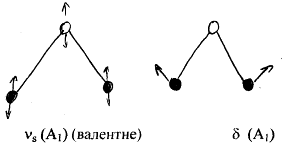
3N-6 = 3 · 3 – 6 = коливання.
(С2
σ1
σ2
; Е) – С2
v
.
ns
– симетричне валентне;
d – деформаційне.
Таблиця типів симетрії і характерівнезвідних представлень групи С2
v
| С2
v
|
Е |
С2
(
z)
|
σv
(xz) |
σv
(yz) |
| A1
|
1 |
1 |
1 |
1 |
| A2
|
1 |
1 |
–1 |
–1 |
| B1
|
1 |
–1 |
1 |
–1 |
| B2
|
1 |
–1 |
–1 |
1 |
Коливання атомів у молекулі, що супроводжується зміною довжини зв’язків, називають валентними
, а коливання, що супроводжуються зміною валентних кутів – деформаційними
. Якщо при коливаннях центр між молекулами не зміщується, то такі коливання називають нормальними
.
|