А прав ли был математик Фибоначчи?

У крупного Итальянского математика Леонардо Фибоначчи (Леонардо Пизанского), автора "Книга об абаке" (1202), которая несколько веков оставалась основным хранилищем сведений по арифметике и алгебре, сейчас встречается чаще всего в связи с замечательной числовой последовательностью 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

Указанная последовательность определяется условиями :

u₁ = 1_, u₂ = 1, u_n+1 = u_n + u_n-1 ( для каждого натурального n > 1 ).

Её члены называются числами Фибоначчи

На рис.1 числа Фибоначчи выражают длины сторон спиральной последовательности квадратов на клетчатой бумаге.

Из данного рисунка несложно получить такое равенство:

u₁ ² +u₂ ² +u₃ ² …u_n ² =u_n u_{n +1} ( для любого n).

рис.1

Великий Итальянский художник-реалист Леонардо да Винчи ( 1452-1519 ) назвал подобную последовательность чисел Фибоначчи "золотым сечением"

Задача автора разъяснить ошибочность чисел Фибоначчи 1, 1, 2, 3, 5,8,13,21, 34, 55, 89, … и определения их как чисел "золотого сечения"

Известно, что мир делится на живую и не живую органику, а у древних народов Пеласги оно означалось знаком, живите .

На основе рис. 2 и по определению делаем вывод, что, знак живой органики отвечает за живые числа (сажени и их доли), а знак неживой органике отвечает за не живые (метрические) числа

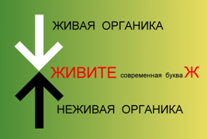
Для математических действий применимы значения чисел, как живой, так и не живой органики.

Далее для своих доводов в пользу утверждений приведем табл. 1 где отображены живые и неживые числа

К живым числам (числам живой органики) относятся такие меры, которые в народе называют саженью, полусаженью, локтем, пястью, пядью, вершком, аршином и т. д, а числовые ряды (3),(2),(1),(0),(-1),(-2),(-3) к не живым числам (числам неживой органики), в дальнейшем мы в этом убедимся.

В таблице мы увидим, как формируются числовые ряды и их последовательность, где их отношения определяются ф. (1-5…)

Таблица 1

Табл. 1 является фрагментом общей корзины "Гармонии Мироздания" или числовой матрицей, если можно сказать ДНК всего Мироздания.

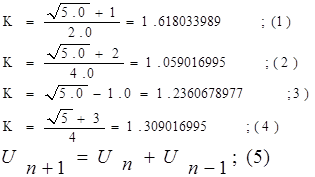
формулы как отношение величин табл. 1

Автор статьи утверждает, что для поиска саженых величин пригодны корни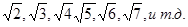

Числа живой органики состоят только из иррациональных чисел.

В общей корзине (матрице) " Гармонии Мироздания" отсутствуют числовые ряды состоящие из метрических чисел Фибоначчи, а это делает их непригодными для дальнейшего математического использования и применения в практике.

Подобная математическая числовая (матрица) корзина "Гармонии Мироздания" в разрозненном виде была у древних цивилизаций вплоть до нашей эпохи инструментарием, для замеров при возведения величественных сооружений пирамид, хором, церквей, храмов, пантеонов и бытовой утвари.

Если мы признаем, что числовая последовательность Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21,34, 55…. , не верна, то и не верна будет его спираль с числовыми рядами рис.1.

Следует обратить внимание на то обстоятельство, что метод расчета подобное ф.(1-5… ) были известны ещё во времена древнего Египта о чем свидетельствуют 11 деревянных панелей. см. рис.3, найденные при вскрытии в начале ХХ века в Саккаре (Египет) погребального сооружения.

Но прежде чем начать говорить о древних измерительных инструментах, как сажени , нам следует осмыслить и происхождение его названия.

Многие слова, ранее употребляемые народами, со временем или трансформировались, или видоизменились, утратив свой первоначальный смысл.

Одним из таких слов является "с" ажень.

Как слово "с" абля, и "с" ажень, имели первоначально свое смысловое значение, как шагать или идущий вперед, с прежним написанием ша жень, как и слово ша бля, ша шки и т. д.

Чтобы убедиться в правильности данного аргумента, возьмём к примеру табл.1 из неё примем за рост человека Маховую сажень 176,0 см., то шаг его всегда будет равен согласно ф.(1) Полуказённой сажени 108,8 см., подобное отношение величин между ростом и ша гом человека в старые времена называли шаженью.

Вот почему вышеперечисленные меры табл.1 называли шаженые меры, осмысливая их для проведения своих замер, умер и обмер как шаг жизни , шаг Господний, шаг Божий.

рис.3

Резонно заметить, а был ли Итальянский математик Фибоначчи первооткрывателем ф.(1-5…) и его числовых рядов??? или он придал им только широкую огласку.

Ведь метод математических расчётов подобное ф. (1-5…) были уже известны и в древнем Египте за долго до рождения итальянского математика Фибоначчи, при том записи, сохранившиеся на 11 деревянных дощечках и формулы Фибоначчи по своему значению не функциональны, по причине отсутствия эталонных саженей и их долевых частей, как в табл.1, а следовательно они не могут иметь своего практического значения.

Существует и тот факт, что на протяжении ХІІІтысячелетий человечество так и не овладело подлинно знаниями использования и применения чисел живой органики.

Фараоны, Египтяне и их рабы не владели тайнами и назначением построек величественных сооружений, как пирамид, они лишь были исполнителями знаний народа Антов.

Но как в науке, так и в практике ничего не следует отвергать без отсутствия, новых более аргументированных доказательств.

В данном случае взамен спирали Фибоначчи с его числовой последовательностью рис. 1, автор статьи приводит спираль "Китовраса"

Спираль "Китовраса" является не только показательной спиралью живой органики, подобная спираль легко вырисовывается, она легко поддается математическим расчётам, абсолютна точна по своему значению, несущая иррациональное происхождение чисел, она гармонично выстраивает последовательность саженей и их долевых частей.

рис.4рис.5

Возьмите спираль "Млечного пути" рис.4, морскую раковину рис.5 в виде улитки, водовороты, спираль "Китовраса" абсолютно совпадает с их очертаниями.

В указанную спираль укладываются все мерила числовой (матрицы) корзины "Гармонии Мироздания" живых чисел, она сформирована на последовательность чисел живой органики, с её числовыми рядами.

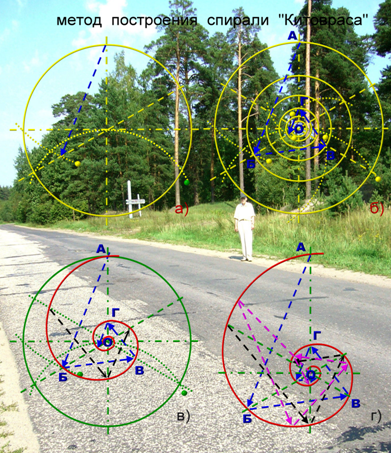
рис. 6

Все отрезки и противолежащие к ним дуги спирали рис. 6 – 7, относятся друг другу строго по ф. (1 – 5…) или

АБ/БВ/ВГ = 1,618033989…,

АО/БО/ВО = 1,618033989…,

Указанные в табл 1 сажени и их долевые части не могут быть, использованы для проведения точных своих расчетов при замерах древних сооружений, данная табл. 1 раскрывает лишь принципиальный подход для поиска живых чисел.

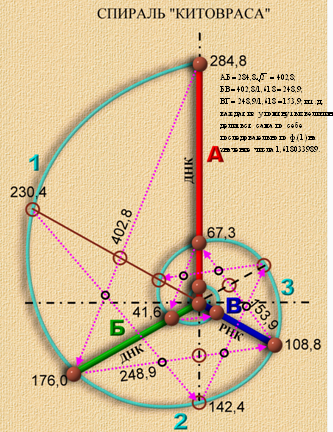
рис.7

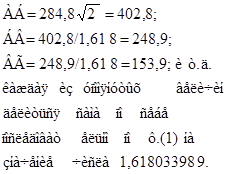
Поиск достаточно точных данных живых чисел определяется иным способом, задача автора заключается в том, чтобы наглядным примером табл.1 находить понимание значений "П I" в живой органике, или как "ПИ" в современном звучании, подобное значение необходимо для построения живого квадрата.

Возьмем сажень 209.05(9) и согласно ф.(2) разделим его на числовое значение 1,059016995³ то в результате получим величину сажени 176.0 (0) см. табл.1.

Подобный метод расчета применял ‘Китоврас" при возведении храма Господнего в Иерусалиме.

Теперь приведём табл. 2 как числовые ряды корзины "Гармонии Мироздания ", созданную на основе нумераций табл. 1, в которой формируются 7 числовых рядов, 3 из них являются основными,и 4 вспомогательными.

О роли и значении таких рядов мы можем поговорить позже

Для расчётов величественных сооружений привлекались "Китоврасы".

"Китоврас" – понятие аллегорическое состоящее из двух корневых основ, Кит – огромный ( великий ) и Врас – вращение (движение).

"Китоврас" изображается в виде созвездия "Стрельца".

Таким образом следует понимать слово "Китоврас", как человек владеющий числовыми знаниями закона вращения Мироздания.

Как делались замеры к примеру пирамид "Китоврасом".

Все стороны и грани, замерялись тремя различными между собой саженями, каждая из которых укладывалась определенное количество раз на заданную величину, при разнице замеров её средняя точка и являлась определяющей для определения высокой точностизаданных расчетов.

Подобный трехмерный расчет позволял на величину 250 метров достигать заданных результатов с точностью плюс, минус 1,5 – 2,0 см.

Такой метод проводимых замеров назывался трехмерным замером , не следует путать его с трехмерным восприятием как (высота, глубина, ширина).

В книге Золото древней Руси, Москва, "Белые альвы"1998г. стр.130 при замерах указывается на сакральное число семь , что мол, данное число является именем Господним, но это не совсем так, посредством числа семь находили те сажени, которыми можно определять без погрешностей указанные величины.

Согласно табл. 1 дан принципиальный расчет церкви Вознесения Господня в парке Коломенском г. Москвы по методу чисел живой органики (живых чисел)

Данная церковь рис. 8, проведена методом трехмерного измерения, величина замеров указана в номерах в соответствии табл. 1

Фото 1

Проведенные автором расчёт Церкви Вознесения в Коломенском, г. Москва по древнерусской системе трехмерного обмера в саженных мерах.

Подобный обмер, как указано в рис. 8 имеет и его план