Курсова робота: Вивчення поняття "символ О"
Зміст
Введення
Розділ 1. Символ О
1.1 Основні визначення, приклади
1.2 Основні співвідношення
1.3 Рішення задач
Розділ 2. Додаток символу О
2.1Асимптотичне рішення трансцендентних рівнянь дійсного змінного
2.2 Асимптотичне рішення інтегралів
2.3Асимптотичне обчислення суми ряду
Література
Введення
Слово асимптотика має грецьке походження й буквально означає "ніколи що не з'єднуються". Вивчаючи конічні перетини, давньогрецькі математики розглядали, зокрема, гіперболи, такі, як графік функції 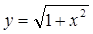 , ,

Які мають прямі y = x і y = -x своїми "асимптотами". При  крива наближається до асимптотам, але ніколи не стикається з ними. У наші дні слово "асимптотика" використовується в більше широкому змісті для позначення будь-якої наближеної величини, що стає усе більше точної в міру наближення деякого параметра до граничного значення. крива наближається до асимптотам, але ніколи не стикається з ними. У наші дні слово "асимптотика" використовується в більше широкому змісті для позначення будь-якої наближеної величини, що стає усе більше точної в міру наближення деякого параметра до граничного значення.
Точні рішення, якщо їх вдається одержати, - це чудово: остаточна відповідь викликає почуття глибокого задоволення. Але й наближене значення іноді виявляється в ціні.
В 1894 році Пауль Бахман придумав позначення для асимптотичного аналізу. У наступні роки його популярності сприяли Едмунд Ландау й ін. Ми зустрічаємо це позначення у формулах на зразок:
 ,(1.1) ,(1.1)
яка говорить нам, що n-е гармонійне число дорівнює натуральному логарифму n плюс константа Ейлера плюс деяка величина, що становить "О велике від 1 на n". Ця остання величина точно не визначена, однак, який би вона не була, позначення "О" дозволяє затверджувати, що вона не перевершує константу, помножену на 1/n.
Величину О(1/n) можна вважати малої, якщо тільки нас не цікавлять величини, що відрізняються від 1/n лише постійним множником.
Додаток символу О можна зустріти в різних областях математики, а також і у фізику. Наприклад, у книзі Панченкова А.Н. "Асимптотичні методи в екстремальних задачах механіки" розглядається застосування асимптотичних методів у рішенні задач аеродинаміки.
Ціль курсової роботи: вивчити поняття "Символ О" і показати його застосування.
Задачі:
1. Вивчити поняття "Символ О", дати визначення.
2. Вивчити й довести основні співвідношення.
3. Показати застосування символу О при рішенні задач.
4. Знайти застосування символу О в різних областях математики.
На підставі поставлених цілей і задач кваліфікаційна робота розбита на дві глави.
Розділ 1 "Символ О" складається із трьох параграфів. У першому параграфі розглядаються основні визначення, приводяться приклади; у другому - формулюються твердження, приводяться їхні докази; третій параграф присвячений рішенню задач.
Розділ 2 "Додатка символу О" висвітлює застосування символу О, а саме, при рішенні трансцендентних рівнянь, при обчисленні інтегралів, при знаходженні суми рядів.
Розділ 1. Символ О.
1.1 Основні визначення, приклади
Визначення 1:
f(n) = O(g(n)) для всіх n Î N (1.1.1) означає, що існує така константа З, що 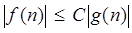 для всіх n Î N; (1.1.2), а якщо позначення O(g(n)) використано усередині формули, то воно позначає функцію f(n), що задовольняє (1.1.2). Значення функції f(n) невідомі, але ми знаємо, що вони не занадто великі. для всіх n Î N; (1.1.2), а якщо позначення O(g(n)) використано усередині формули, то воно позначає функцію f(n), що задовольняє (1.1.2). Значення функції f(n) невідомі, але ми знаємо, що вони не занадто великі.
Символ "О" включає невизначену константу С, кожне входження О може мати на увазі різні З, але кожна із цих констант не залежить від n.
Приклад 1: ми знаємо, що сума квадратів перших n натуральних чисел дорівнює
n
= 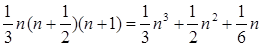 . .
Можна записати n
= О(n3
),
тому що
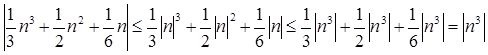
для всіх цілих n. Можна одержати більше точну формулу
n
= 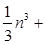 О(n2
), тому що О(n2
), тому що
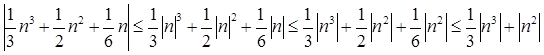
для всіх цілих n. Можна також недбало відкинути частина інформації й записати n
= О(n10
).
Визначення О не змушує нас давати найкращу оцінку.
Розглянемо приклад, коли змінна n – не целочисленна.
Приклад 2:
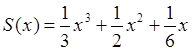 , ,
де х – речовинне число.
Тут уже не можна сказати, що S(x) = O(x3
), тому що відношення 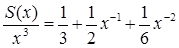 необмежено росте при х®0. Не можна також сказати, що S(x) = O(x), тому що відношення необмежено росте при х®0. Не можна також сказати, що S(x) = O(x), тому що відношення  необмежено росте, коли х прагне до нескінченності. Виходить, ми не можемо використовувати символ "О" для оцінки S(x). необмежено росте, коли х прагне до нескінченності. Виходить, ми не можемо використовувати символ "О" для оцінки S(x).
Ця дилема дозволяється завдяки тому, що на змінні, використовувані із О, звичайно накладаються які-небудь обмеження. Якщо, наприклад, ми поставимо умову, що 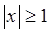 , або що , або що 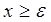 , де e - довільна позитивна константа, або що х – ціле число, то ми зможемо записати S(x) = O(x3
). Якщо ж накладена умова , де e - довільна позитивна константа, або що х – ціле число, то ми зможемо записати S(x) = O(x3
). Якщо ж накладена умова 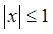 або або 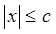 , де з – довільна позитивна константа, то в цьому випадку S(x) = O(x). "О велике" залежить від контексту, від обмежень на використовувані змінні. , де з – довільна позитивна константа, то в цьому випадку S(x) = O(x). "О велике" залежить від контексту, від обмежень на використовувані змінні.
Ці обмеження часто задаються у вигляді граничних співвідношень.
Визначення 2: співвідношення f(n) = O(g(n)) при n®¥ означає, що існують дві константи С и n0
, такі, що
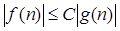 при всіх n ³ n0
.(1.1.3) при всіх n ³ n0
.(1.1.3)
Зауваження 1: Значення С и n0
можуть бути різними для різних О, але вони не залежать від n.
Визначення 3: запис f(х) = O(g(х)) при х®0 означає, що існують дві константи С и e, такі, що
 ,якщо тільки ,якщо тільки  .(1.1.4) .(1.1.4)
Тепер О представляє невизначену функцію й одну або дві невизначені константи, що залежать від контексту.
Зауваження 2: запис 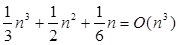 коректний, але в цій рівності не можна міняти місцями праву й ліву частини. У противному випадку ми можемо прийти до безглуздих висновків, на зразок n = n2
, виходячи з вірних тотожностей n = О(n2
) і n2
= О(n2
). коректний, але в цій рівності не можна міняти місцями праву й ліву частини. У противному випадку ми можемо прийти до безглуздих висновків, на зразок n = n2
, виходячи з вірних тотожностей n = О(n2
) і n2
= О(n2
).
Працюючи із символом "О" ми маємо справу з однобічними рівностями. Права частина рівняння містить не більше інформації, чим ліва, і фактично може містити менше інформації; права частина є "огрубінням" лівої.
Якщо говорити строго формально, то запис O(g(n)) позначає не якусь одну функцію f(n), а відразу множина функцій f(n), таких, що 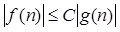 для деякої константи С. Звичайна формула g(n), що не включає символ О, позначає множину, що містить одну функцію f(n) = g(n). Якщо S і T суть множини функцій від n, то запис S + T позначає множину всіх функцій виду f(n) + g(n), де f(n)ÎS і g(n)ÎT; інші позначення начебто S – T, ST, S/T, для деякої константи С. Звичайна формула g(n), що не включає символ О, позначає множину, що містить одну функцію f(n) = g(n). Якщо S і T суть множини функцій від n, то запис S + T позначає множину всіх функцій виду f(n) + g(n), де f(n)ÎS і g(n)ÎT; інші позначення начебто S – T, ST, S/T,  , е, ln S визначаються аналогічно. Тоді "рівність" між двома такими множинами функцій є теоретико-множинне включення; знак "=" у дійсності означає "(". , е, ln S визначаються аналогічно. Тоді "рівність" між двома такими множинами функцій є теоретико-множинне включення; знак "=" у дійсності означає "(".
Приклад 3: "Рівняння" 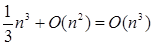 означає, що S1
Í S2
, де S1
є множину всіх функцій виду означає, що S1
Í S2
, де S1
є множину всіх функцій виду 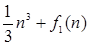 , для яких найдеться константа З1
, така, що , для яких найдеться константа З1
, така, що 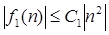 , а S2
є множина всіх функцій , а S2
є множина всіх функцій 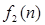 , для яких найдеться константа З2
, така, що , для яких найдеться константа З2
, така, що 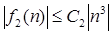 . .
Можна строго довести це "рівність", якщо взяти довільний елемент із лівої частини й показати, що він належить правій частині: нехай 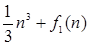 таке, що таке, що 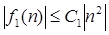 , варто довести, що існує така константа З2
, що , варто довести, що існує така константа З2
, що  . Константа . Константа  вирішує проблему, тому що вирішує проблему, тому що 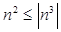 для всіх цілих n. для всіх цілих n.
Зауваження 3: Якщо у формулі використовується трохи змінних, то символ О представляє множину функцій від двох або більше змінних, а не тільки від однієї. В область визначення кожної функції входять всі змінні, які в даному контексті "вільні" для зміни.
Отут є деяка тонкість через те, що змінні можуть мати сенс лише в частині вираження, якщо вони зв'язані знайомий ( або подібним.
Приклад 4:
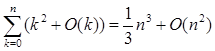 , ,
ціле n ³ 0.(1.1.5)
Вираження k2
+ O(k) у лівій частині відповідає множині всіх функцій від двох змінних виду k2
+ f(k, n), для яких найдеться константа З, така, що 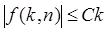 для 0 £ k £ n. Сума таких множин функцій для 0 £ k £ n є множину всіх функцій g(n) виду для 0 £ k £ n. Сума таких множин функцій для 0 £ k £ n є множину всіх функцій g(n) виду
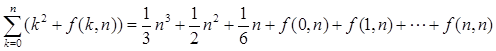 , ,
де f задовольняє сформульованій умові. Оскільки
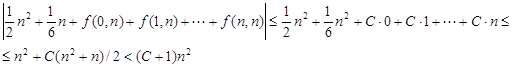
те всі такі функції g(n) належать правій частині (1.1.5); отже, (1.1.5) справедливо.
1.2 Основні співвідношення
Співвідношення 1: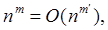 якщо якщо 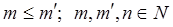 .(1.2.1) .(1.2.1)
Доказ:
Нехай 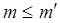 , тоді , тоді 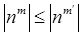 по властивості ступеня й модуля. по властивості ступеня й модуля. 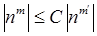 , де З = 1. А по визначенню (1.1.2) символи Об це й означає, що , де З = 1. А по визначенню (1.1.2) символи Об це й означає, що 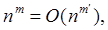 при при 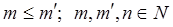 . Співвідношення 1 доведене. . Співвідношення 1 доведене.
Співвідношення 2: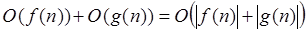 .(1.2.2) .(1.2.2)
Доказ:
Покажемо строго відповідно до теоретико-множинного визначення символу О, що ліва частина є підмножиною правої частини.
Будь-яка функція з лівої частини має вигляд a(n) + b(n), і існують константи m0
, B, n0
, C, такі, що
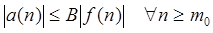 и. и.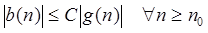
Отже, функція в лівій частині
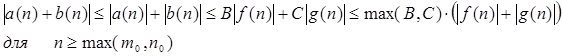
А, виходить, по визначенню символу О ліва частина належить правій частині. Співвідношення 2 доведене.
Співвідношення 3: f(n) = O(f(n));(1.2.3)
Доказ:
Для будь-якої функції f(n) вірна нерівність  . . 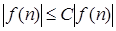 , де З = 1. По визначенню символу О (1.1.2) це й означає, що f(n) = O(f(n)). Співвідношення 3 доведене. , де З = 1. По визначенню символу О (1.1.2) це й означає, що f(n) = O(f(n)). Співвідношення 3 доведене.
Співвідношення 4: O(f(n))O(g(n)) = O(f(n)g(n));(1.2.4)
Доказ:
Покажемо відповідно до теоретико-множинного визначення символу О, що ліва частина є підмножиною правої частини.
У лівій частині функції мають вигляд a(n) × b(n), такі, що існують константи В, З, n0
, m0
, що
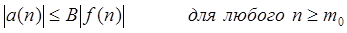 і і
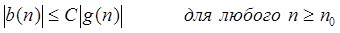 . .
Тоді 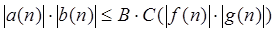 для будь-якого n ³ max(n0
, m0
,). Значить ліва частина належить правій частині, а, отже, є підмножиною правої частини по визначенню символу О. Співвідношення 6 доведене. для будь-якого n ³ max(n0
, m0
,). Значить ліва частина належить правій частині, а, отже, є підмножиною правої частини по визначенню символу О. Співвідношення 6 доведене.
Співвідношення 5: O(O(f(n))) = O(f(n));(1.2.5)
Доказ:
Покажемо, що ліва частина є підмножиною правої частини.
Функція з лівої частини має вигляд a(n) такий, що існують позитивні константи З, В, n0
, m0
такі, що
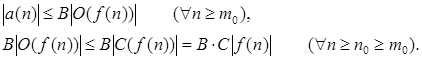
Отже, по визначенню ліва частина є підмножиною правої частини. Співвідношення 5 доведене.
Співвідношення 6: С× O(f(n)) = O(f(n)),якщо З – константа;(1.2.6)
Доказ:
Існує така константа В, що 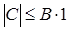 , по визначенню (1.1.1) З = О(1). Тоді З × O(f(n)) = О(1) × O(f(n)) = (по 1.2.4) = O(f(n)). , по визначенню (1.1.1) З = О(1). Тоді З × O(f(n)) = О(1) × O(f(n)) = (по 1.2.4) = O(f(n)).
Співвідношення доведене.
Співвідношення 7: O(f(n)g(n)) = f(n)O(g(n)).(1.2.7)
Доказ:
Покажемо, що ліва частина є підмножиною правої частини.
У лівій частині функції мають вигляд a(n), такі, що існують константи З, n0
, що
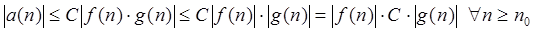 . .
По визначенню символу О ми одержуємо вірну рівність (1.2.7). Співвідношення 7 доведене.
Співвідношення 8: O(f(n)2)
= O(f(n))2
.(1.2.8)
Доказ:
O(f(n)2)
= O(f(n) · f(n)) = (по 1.2.7) = f(n) · O(f(n)) = (по 1.2.3) = О(f(n)) · O(f(n)) = O(f(n))2
Співвідношення доведене.
Співвідношення 9: е(f(n))
= 1 + O(f(n)), якщо f(n) = О(1)(1.2.9)
Доказ:
е(f(n))
= еg(n)
, де 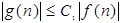 . .
Так як. f(n) = О(1), тобто
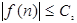 , те , те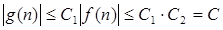 . .
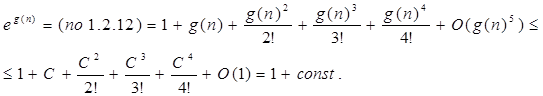
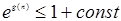 . Значить е(f(n))
= 1 + O(f(n)). . Значить е(f(n))
= 1 + O(f(n)).
Співвідношення доведене.
Співвідношення 10: Якщо сума 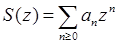 сходиться абсолютно для деякого комплексного числа z = z0
, те сходиться абсолютно для деякого комплексного числа z = z0
, те
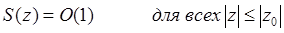 . .
Доказ:
Дане співвідношення очевидно, оскільки
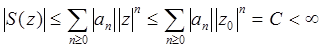 . .
Співвідношення доведене.
Зауваження 4: Зокрема, S(z) = O(1) при z ® 0 і S(1/n) = O(1) при n ®¥ при тім тільки умові, що S(z) сходиться хоча б для одного ненульового значення z. Ми можемо використовувати цей принцип для того, щоб, відкинувши хвіст статечного ряду, починаючи з будь-якого зручного місця, оцінити цей хвіст через О. Так, наприклад, не тільки S(z) = O(1), але й
S(z) = a0
+ O(z), S(z) = a0
+ a1
z + O(z2
),
і т.д., оскільки
 , ,
а остання сума, як і сама S(z), абсолютно сходиться при z = z0
і є О(1).
У таблиці №1 наведені самі корисні асимптотичні формули [2], половина з яких отримана шляхом відкидання членів статечного ряду відповідно до цього правила.
Таблиця №1Асимптотичні апроксимації, справедливі при n ®¥ і z ® 0
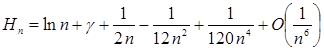 (1.2.10) (1.2.10) |
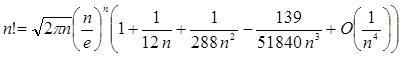 (1.2.11) (1.2.11) |
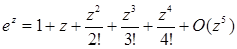 (1.2.12) (1.2.12) |
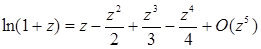 (1.2.13) (1.2.13) |
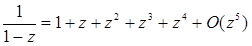 (1.2.14) (1.2.14) |
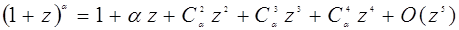 (1.2.15) (1.2.15) |
Асимптотичні формули для Hn
, n! не є початковими відрізками збіжних рядів; якщо необмежено продовжити ці формули, те отримані ряди будуть розходитися при всіх n.
Говорять, що асимптотична апроксимація має абсолютну погрішність O(g(n)), якщо вона має вигляд f(n) + O(g(n)), де f(n) не включає О. Апроксимація виду f(n)(1 + O(g(n))) має відносну погрішність O(g(n)), якщо f(n) не включає О. Наприклад, апроксимація Hn
у таблиці №1 має абсолютну погрішність O(n-6
); апроксимація n! - відносну погрішність O(n-4
). (Права частина (1.2.11) не така, як потрібно, - f(n)(1 + O(n-4
)), але її можна переписати як
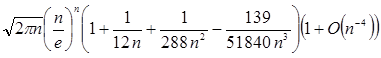 . .
Абсолютна погрішність цієї апроксимації є O(nn-3.5
e-n
). Абсолютна погрішність співвідноситься із числом вірних десяткових цифр праворуч від десяткової крапки, які зберігаються після відкидання члена О; відносна погрішність пов'язана із числом вірних "значущих цифр".
1.3 Рішення задач
Задача 1. Що невірно в наступних міркуваннях? Оскільки n = O(n) і 2n = O(n) і так далі, те містимо, що 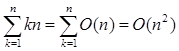 ? ?
Рішення:
Заміна kn на O(n) має на увазі різні Із для різних k; а потрібно, щоб усе О мали загальну константу. У дійсності, у цьому випадку потрібно, щоб О позначало множину функцій двох змінних, k і n. Правильно буде записати
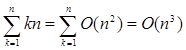 . .
Задача 2. Доведіть або спростуйте: О(f(n) + g(n)) = f(n) + O(g(n)), якщо f(n) і g(n) позитивні для всіх nÎN.
Рішення:
Твердження невірне.
Нехай f(n) = n2
, а g(n) = 1. Знайдемо таку функцію j(n), яка б належала лівій множині, але не належала б правій множині, тобто ($З1
) ("n) [j(n) £ C1
(n2
+ 1)] і ("З2
) ($n³n0
) [j(n) > n2
+ C2
].
Візьмемо j(n) = 2n2
.
1). Нехай З1
= 3, тоді ("n³n0
) 2n2
£ 3(n2
+ 1). Значить функція j(n) належить лівій множині.
2). ("З2
) ($n> ) 2n2
> n2
+ C2
. Значить функція j(n) не належить правій множині. ) 2n2
> n2
+ C2
. Значить функція j(n) не належить правій множині.
Задача 3. Доведіть або спростуйте: cos O(x) = 1 + O(x2
) для всіх речовинних х.
Рішення:
Якщо функція g(x) належить лівій частині так, що g(x) = cos y для деякого y, причому 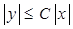 для деякої константи З, то g(x) = cos y = 1 - 2sin2
(y/2) £ 1 = 1 + 0 × х2
. Значить існує така константа В, що g(x) £ 1 + В × х2
. Отже, множина з лівої частини втримується в правій частині, і формула вірна. для деякої константи З, то g(x) = cos y = 1 - 2sin2
(y/2) £ 1 = 1 + 0 × х2
. Значить існує така константа В, що g(x) £ 1 + В × х2
. Отже, множина з лівої частини втримується в правій частині, і формула вірна.
Задача 4. Доведіть, що 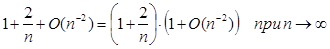 . .
Рішення:
Перетворимо ліву частину в такий спосіб:
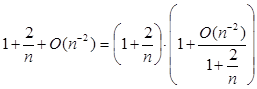 . .
Помітимо, що 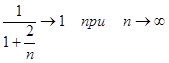 , тоді , тоді  , де З – константа, тоді можна записати по визначенню символу О, що , де З – константа, тоді можна записати по визначенню символу О, що 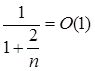 . Використовуючи це для перетвореної рівності, одержуємо, що . Використовуючи це для перетвореної рівності, одержуємо, що
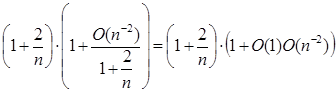 = (по 1.2.4) = (по 1.2.4)

Що й було потрібно довести.
Задача 5. Обчислите 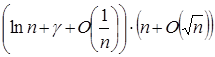 при nÎN. при nÎN.
Рішення:
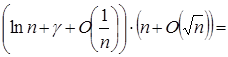
 (по 1.2.6) (по 1.2.6)
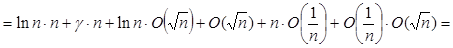 (по 1.2.3) (по 1.2.3)
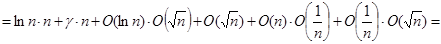 (по 1.2.4) (по 1.2.4)
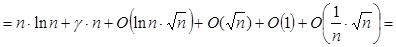 (по 1.2.2) (по 1.2.2)
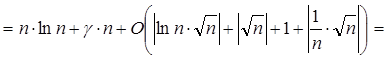

Задача 6. Обчислите (n + 2 + O(n-1
))n
з відносною погрішністю O(n-1
), при n®¥.
Рішення:
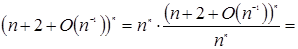
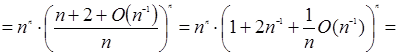 (по 1.2.3 і 1.2.4) (по 1.2.3 і 1.2.4)
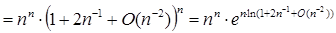
При n®¥ k = (2n-1
+ O(n-2
)) ® 0, тоді ln (1 + k) ® 0. Тоді при n®¥ ln (1 + k) = k.
 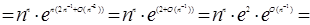 (по 1.2.9) (по 1.2.9)
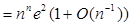 . .
Задача 7. Доведіть, що  , при nÎN, n®¥. , при nÎN, n®¥.
Рішення:
Покажемо, що 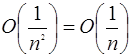 .(*) .(*)
По визначенню 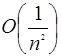 - функція аn
така, що - функція аn
така, що  . .
Одержуємо, що 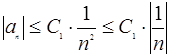 , значить , значить 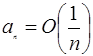 . .
Тепер доведемо, що  : :
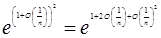 = (по 1.2.4 і 1.2.6) = = (по 1.2.4 і 1.2.6) = 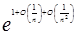 = (по (*)) = = (по (*)) =
 (по 1.2.6) = (по 1.2.6) =  (по 1.2.9) = (по 1.2.9) =
 (по 1.2.6) = (по 1.2.6) = . .
Розділ 2. Додаток символу О
2.1 Асимптотичне рішення трансцендентних рівнянь: дійсного змінного
Приклад 1.
Розглянемо рівняння
x +th x = u,
де u - дійсний параметр,  - гіперболічний тангенс [6], - гіперболічний тангенс [6],  , х і th x – безперервні, строго зростаючі функції на всій числовій прямій. , х і th x – безперервні, строго зростаючі функції на всій числовій прямій.
Знайдемо асимптотичне наближення для кореня:
1). Функція u(x) = x +th x безперервна й строго монотонна на R. По теоремі О безперервність зворотної функції, існує зворотна до неї функція х(і), безперервна й строго монотонна на Еи
= R.
Тому що при х®¥ і(х)®¥, те при й®¥ х(і)®¥.
Нехай і®¥, тоді х®¥ і  . .
Виходить, х(і) ~ і, при й®¥. Це перше асимптотичне наближення для кореня.
2). Приведемо рівняння до виду:
x = і - th x.
 +З, де З – деяка константа. По визначенню символу О thx = 1+O(1). +З, де З – деяка константа. По визначенню символу О thx = 1+O(1).
x = і – 1 + О(1) - це друге асимптотичне наближення кореня.
3). Доведемо, що е-2х
= О(е-2і
):(2.1.1)
підставимо друге асимптотичне наближення кореня
е-2х
= е-2(і – 1 + О(1))
= е-2і
× е2
× еО(1)
= (по 1.2.3 і 1.2.9) = е2
О(е-2і
)(1 + О(1))×=
(по 1.2.3) = е2
О(е-2і
)(2О(1)) = (по 1.2.6 і 1.2.4) = О(е-2і
).
Розкладемо th x у ряд [6], зручний при більших х:
th x = 1 – 2е-2х
+ 2е-4х
– 2е-6х
+…(х > 0)
Тоді по теоремі [3]:(2.1.2)
якщо ряд  сходиться при сходиться при  , тоді для фіксованого n , тоді для фіксованого n  у будь-якому колі у будь-якому колі  , де , де  .Ряд – 2е-2х
+ 2е-4х
– 2е-6х
+…сходиться при х > 0, тобто .Ряд – 2е-2х
+ 2е-4х
– 2е-6х
+…сходиться при х > 0, тобто  і його сума дорівнює th x - 1. Виходить, по теоремі: th x - 1 = О(е-2х)
, тобто th x=О(е-2х)
+1.Тоді x = і - th x = і – 1 + О(е-2х)
= (по 2.1.1) = і – 1 + О(О(е-2і
)) =(по 1.2.5) = і – 1 + О(е-2і
).Таким чином, x = і – 1 + О(е-2і
) - цей третє асимптотичне наближення кореня. і його сума дорівнює th x - 1. Виходить, по теоремі: th x - 1 = О(е-2х)
, тобто th x=О(е-2х)
+1.Тоді x = і - th x = і – 1 + О(е-2х)
= (по 2.1.1) = і – 1 + О(О(е-2і
)) =(по 1.2.5) = і – 1 + О(е-2і
).Таким чином, x = і – 1 + О(е-2і
) - цей третє асимптотичне наближення кореня.
4). Доведемо, що е-2х
= е-2і+2
+ О(е-4і
):(2.1.3)підставимо третє асимптотичне наближення кореня
 (по 1.2.9) (по 1.2.9)

 (по 1.2.6) (по 1.2.6)
(по 1.2.3 і 1.2.4)  . .
Ряд 2е-4х
– 2е-6х
+ 2е-8х
– 2е-10х
+…сходиться при х > 0, тобто  і його сума дорівнює th x – 1 + 2е-2х
. Виходить, по теоремі: th x – 1 + 2е-2х
= О(е-4х)
, тобто th x=О(е-4х)
+1 - 2е-2х
. і його сума дорівнює th x – 1 + 2е-2х
. Виходить, по теоремі: th x – 1 + 2е-2х
= О(е-4х)
, тобто th x=О(е-4х)
+1 - 2е-2х
.
Тоді
x = і - th x = і – 1 + 2е-2х
+ О(е-4х)
= (по 2.1.3) =
= і – 1 + 2(е-2і+2
+ О(е-4і
)) + О(е-4х)
= (по 1.2.6) =
= і – 1 + 2е-2і+2
+ О(е-4і
) + О(е-2х
× е-2х)
= (по 2.1.1) =
= і – 1 + 2е-2і+2
+ О(е-4і
) + О(О(е-2і
)× О(е-2і
)) = (по 1.2.4) =
= і – 1 + 2е-2і+2
+ О(е-4і
) + О(О(е-4і
)) = (по 1.2.5) =
= і – 1 + 2е-2і+2
+ О(е-4і
) + О(е-4і
) = і – 1 + 2е-2і+2
+ 2О(е-4і
) = (по 1.2.6) =
= і – 1 + 2е-2і+2
+ О(е-4і
).
Таким чином, x = і – 1 + 2е-2і+2
+ О(е-4і
) - цей четверте асимптотичне наближення кореня.
Продовжуючи цей процес, одержимо послідовність наближень із помилками, асимптотичний порядок яких постійно убуває. Збіжність цієї послідовності при необмеженому зростанні числа кроків на основі проведених міркувань побачити важко, але чисельні можливості цього процесу можна оцінити, взявши, наприклад, і = 5:
1) х = 5;
2) х = і – 1 + О(1) = 5 – 1 = 4; (не враховуємо помилку О(1))
3) x = і – 1 + О(е-2і
) = 5 – 1 = 4; (не враховуємо помилку О(е-2і
))
4) x = і – 1 + 2е-2і+2
+ О(е-4і
) = 5 – 1 + 0,000670925…=4,000670925..... (не враховуємо помилку О(е-4і
))
Точне значення, отримане стандартними чисельними методами, дорівнює 4,0006698...
Приклад 2.
Знайдемо більших позитивних корінь рівняння
x tg x = 1
Це рівняння можна звернути в такий спосіб:
 , ,
де n – ціле число, а арктангенс приймає значення в інтервалі  , знаходимо, що x ~ np при (n → ¥). , знаходимо, що x ~ np при (n → ¥).
Якщо x > 1, то [6]

1). По теоремі (2.1.2)
 . .
 . .
2). 
По теоремі (2.1.2)
 . Тоді . Тоді  . .
 . .
3). 
По теоремі (2.1.2)
 . Тоді . Тоді  . .
 . .
І так далі.
2.2Асимптотичне рішення інтегралів
Приклад 1. Обчислити  при х > 1. при х > 1.
Розкладемо в ряд [6]:
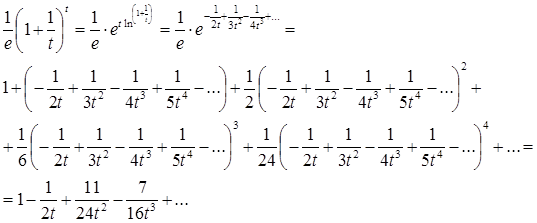
По теоремі (2.1.2)
 , тобто , тобто  . .

Приклад 2. Обчислити  при e®+0, при e®+0,  , А(х) - східчаста функція: А(х) = 0 при х < 0, А(х) = Аk
, k £ x < k + 1, Аk
= а1
+ а2
+…+аk
, аk
= k -1
. Причому , А(х) - східчаста функція: А(х) = 0 при х < 0, А(х) = Аk
, k £ x < k + 1, Аk
= а1
+ а2
+…+аk
, аk
= k -1
. Причому  . .
Скористаємося асимптотичною формулою [4]
 , ,
де g - постійна Ейлера  . Уведемо функцію Ã(х) = lnx + g. . Уведемо функцію Ã(х) = lnx + g.

 . .
Останній інтеграл має порядок О(e ln e) при e®+0, а передостанній – дорівнює -g/2, так що
 . .
S(e) = I + J, де
 . .
Оцінимо інтеграл J. Нехай  , тоді " k ³ 1 , тоді " k ³ 1
 . .
Ологарифмуємо  , одержимо , одержимо  . .
Значить 
Отже,
 . .
Одержуємо, що
 . .
2.3Асимптотичне обчислення суми ряду
При знаходженні суми ряду нерідко використовується формула підсумовування Ейлера [2]:

де 
Вk
– числа Бернуллі, Вm
({x}) – багаточлен Бернуллі.
Вk
= (-1)k
b2k
. [6]
 . Коефіцієнти bk
обчислюються, використовуючи теорему О одиничність розкладання функції в статечної ряд: . Коефіцієнти bk
обчислюються, використовуючи теорему О одиничність розкладання функції в статечної ряд:

шляхом дорівнюючи коефіцієнтів:
коефіцієнт при х: b0
= 1,
коефіцієнт при хk
:


Приклад 1. Знайти  . .
По 1.2.10 Нk
= ln k + O(1). Тоді
 . .

Застосуємо формулу підсумовування Ейлера:




 . .
Приклад 2. Знайти 
Застосуємо формулу підсумовування Ейлера:



Приклад 3. Знайти асимптотику при n ®¥ суми 
Члени цієї суми швидко ростуть із ростом номера, так що головний член асимптотики дорівнює останньому члену суми: S(n) ~ n!, n ®¥. Дійсно,

Отже,

Література
1. Брейн, Н.Г. Асимптотичні методи в аналізі. – К., 2006
2. Грехем, Р. Конкретна математика. Основи інформатики. – К.,2004
3. Олвер, Ф. Введення в асимптотичні методи й спеціальні функції. – К., 2004
4. Панченков, О.М. Асимптотичні методи в екстремальних задачах механіки. – К., 2004
5. Федорюк, М.В. Асимптотика: інтеграли й ряди. – К., 2005
6. Фихтенгольц, Г.М. Курс диференціального й інтегрального вирахування. – К., 2000
|