Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа № 4
Секция: математика
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
по теме
Доказательства неравенств с помощью одномонотонных последовательностей
Позолотина Наталья Андреевна, 9б
класс,
МОУ СОШ №4 Центрального района.
224-49-85
Руководитель: Тропина Наталья Валерьяновна,
кандидат педагогических наук,
доцент кафедры математического анализа НГПУ.
(Работа выполнена в МОУ СОШ №4)
Новосибирск 2008
Содержание
Введение
1. Основные понятия и определения
2. Обоснование метода одномонотонных последовательностей для случая с произвольным числом переменных
2.1 Доказательство неравенств с минимальным числом переменных
2.2 Случай с двумя последовательностями из двух переменных
Упражнения
2.3 Случай с двумя последовательностями из трех переменных
Упражнения
2.4 Случай с двумя последовательностями из n переменных
Упражнения
2.5 Случай с n последовательностями из n переменных
Упражнения
Заключение
Список использованной литературы
Введение
В школьном курсе математике мы изучали доказательства неравенств в основном двумя способами:
- сведение к очевидному с помощью равносильных преобразований;
- графически (исследование свойств и построение графиков функции)
Не существует универсального способа доказательства всех неравенств, и более того, не существует конкретных указаний для выбора способа доказательства. Поэтому любой новый способ доказательства неравенств представляет особый интерес.
В данном работе мы рассмотрим один из таких способов: доказательство неравенств с помощью одномонотонных последовательностей.
Работа состоит из 2-х параграфов. В первом параграфе я объясняю основные определения, которые нам понадобятся для работы. Во втором параграфе находится основная работа с примерами и упражнениями.
1. Основные понятия и определения
В данном параграфе мы рассмотрим основные понятия и определения, которые нам понадобятся для дальнейшей работы.
Определение 1. Множество – это совокупность, собрание, набор некоторых объектов по какому – либо общему для них признаку.
Определение 2. Натуральные числа N – это целые положительные числа 1, 2, 3, 4, 5,…
Определение 3. Целые числа Z – это числа 0, +1, +2, +3, +4, +5…:
Z = N -N -N {0} {0}
Определение 4. Рациональные числа Q– это числа представимые обычными дробями в виде 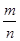 , где mє
Z, nє
N (или конечными, или бесконечными периодичными дробными). , где mє
Z, nє
N (или конечными, или бесконечными периодичными дробными).
Определение 5. Иррациональные числа I – это числа, представимые бесконечными непериодическими десятичными дробями и непредставимые в виде 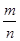 . .
Определение 6. Вещественные (действительные) числа R – объединение множества рациональных и иррациональных чисел.
R=Q I I
Определения 7. Неравенство – соотношение между величинами, показывающее, что одна величина больше или меньше другой.
Например: 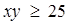 , , 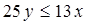
Известно, что все неравенства подчиняются определенным свойствам, таким как:
а) a<b, b<c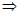 a<c a<c
b) a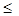 b, b b, b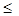 a a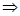 a=b a=b
c) a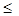 b b 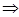 a+c a+c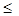 b+c b+c
d) a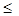 0 0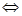 -a -a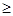 0 0
Определения 8. Доказать неравенство – установить истинность неравенства.
Неравенства бывают разными: с одной, двумя и более переменными, со степенями. Ля каждого неравенства существует свой способ доказательств. Мы рассмотрим еще один способ: через одномонотонные последовательности.
Определение 9. Следствие – из двух неравенств одно является следствием другого, если область истинности второго неравенства содержит в себе область истинности первого неравенства.
Обозначение: f1
(x)>f2
(x)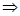 ц1
(x)>ц2
(x) – второе неравенство – следствие первого. ц1
(x)>ц2
(x) – второе неравенство – следствие первого.
Определение 10. Два неравенства называются равносильными, если каждое из них является следствием другого. Иначе это можно сформулировать так: два неравенства считаются равносильными, если их множества значений переменных, для которых они истинны, совпадают.
Обозначаются равносильные неравенства: f1
(x)>f2
(x)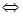 ц1
(x)>ц2
(x) ц1
(x)>ц2
(x)
Эти определения аналогичны соответствующим определениям для уравнений. Как и для уравнений, можно сформулировать утверждения о действиях, преобразующих данное неравенство в равносильное ему. Такими действиями могут быть:
– прибавление к обеим частям неравенства одного слагаемого;
– перенос слагаемого с противоположным знаком из одной части неравенства в другую;
– умножение обеих частей на положительное число или положительную функцию и т.д.
Следует, однако, производя эти действия, следить, чтобы не изменилась область допустимых значений, так как иначе будет нарушена равносильность этих неравенств.
Определение 11. Метода математической индукции – метод доказательства неравенств, путем схожести доказательств от самого легкого к самому сложному.
Например, Р(n) – некоторое утверждение, зависимое от n є
N
1) Проверяем правдивость Р(1)
2) Предполагаем, что P(k) истинно
3) Доказываем истинность Р(k+1)
4) Заключаем, что Р(n) истинно для любых n.
Определение 12. Одномонотонные последовательности – это последовательности чисел вида (
а1
а2
… аn
)(
b1
b2 …
bn
)
записанных в виде таблицы, где наибольшее из чисел а1
а2
… аn
находится над наибольшим числом из чисел b1
b2 …
bn
и второе по величине из чисел а1
а2
… аn
над вторым по величине из чисел b1
b2 …
bn
и т.д., другими словами обе последовательности одновременно возрастающие или одновременно убывающие.
Определение 13. Произведение одномонотонных последовательностей (а1
, а2
, …аn
), (b 1
, b2
,…bn
), …( d 1
, d 2
,…, dn
) это число вида
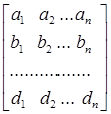 = а1
b1
…d1
+а2
b2
…d2
+ …+an
bn
…dn = а1
b1
…d1
+а2
b2
…d2
+ …+an
bn
…dn
2. Обоснование метода одномонотонных последовательностей для случая с произвольным числом переменных
Данный параграф разбит на пункты, в которых мы попробуем прийти к самому общему доказательству, для случая k последовательностей с n числом переменных, с помощью метода математической индукции.
2.1 Доказательство неравенств с минимальным числом переменных
а1
*b1
– неравенство с минимальным числом переменных. Тогда
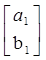 = a1
b1. = a1
b1.
Так как это неравенство минимальное из всех существующих, то сравнивать с похожим неравенством его просто невозможно.
2.2
Случай с двумя последовательностями из двух переменных
Если 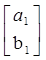 = a1
b1
. то = a1
b1
. то 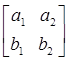 =а1
b1
+а2
b2 =а1
b1
+а2
b2
Теорема 1. Пусть (а1
а2)
 (b
1
b
2
) – одномонотонные последовательности. Тогда (b
1
b
2
) – одномонотонные последовательности. Тогда
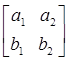 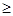 
Доказательство
Действительно,
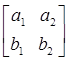 – –  =a1
b1
+a2
b2
-a1
b2
-a2
b1
= (a1
-a2
) =a1
b1
+a2
b2
-a1
b2
-a2
b1
= (a1
-a2
)  (b1
-b2
) (b1
-b2
)
Так как последовательности (а1
а2
)(b1
b2
) одномонотонны, то числа a1
-a2
и b1
-b2
имеют одинаковый знак. Поэтому
(a1
-a2
) (b1
-b2
) (b1
-b2
) 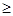 0. 0.
Теорема доказана.
Упражнения
Данные ниже упражнения мы решим с помощью Теоремы 1
Упражнение №1
.
Пусть a и b – положительные вещественные числа.
Доказать неравенство
a3
+b3
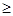 a2
b+b2
a. a2
b+b2
a.
Доказательство.
Заметим, прежде всего, что
a3
+b3
= , a2
b+b2
a = , a2
b+b2
a = 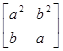
А так как последовательности (a2
, b2
), (a, b) одномонотонны, то
 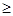 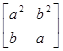
А это значит, что a3
+b3
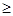 a2
b+b2
a. a2
b+b2
a.
Что и требовалось доказать.
Докажем это же неравенство, но другим способом.
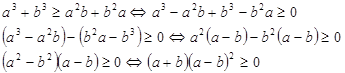
Значит a3
+b3
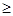 a2
b+b2
a. a2
b+b2
a.
Что и требовалось доказать.
Мы не можем сказать какой из методов доказательства решения легче, так как в данном случае оба метода решения неравенства примерно одинаковые по сложности.
Упражнение №2
.
Пусть a и b – положительные вещественные числа.
Доказать неравенство.
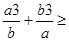 а2
+b2
. а2
+b2
.
Доказательство.
Заметим, прежде всего, что
а2
+b2
=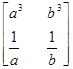 , , 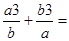 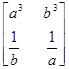 , ,
А так как последовательности (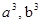 ), ( ), (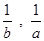 ) одномонотонны, то ) одномонотонны, то
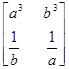 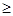 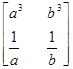 . .
Что и требовалось доказать.
2.3 Случай с двумя последовательностями из трех переменных
Рассмотрим последовательность (а1
,а2
,а3
) и (b 1
, b2
,b3
), и запишем в виде таблицы
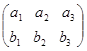
Если последовательность (а1
,а2
,а3
) (b1
, b2
,b3
) записанных в виде таблицы, где наибольшее из чисел а1
,а2
,а3
находиться над наибольшим из чисел b 1
,b2
,b3
, а второе по величине а1
,а2
,а3
находиться над вторым по величине из чисел b 1
,b2
,b3
, и где наименьшее из чисел а1
,а2
,а3
находиться над наименьшим из чисел b 1
,b2
,b3
то последовательность одномонотонная. (b1
, b2
,b3
) записанных в виде таблицы, где наибольшее из чисел а1
,а2
,а3
находиться над наибольшим из чисел b 1
,b2
,b3
, а второе по величине а1
,а2
,а3
находиться над вторым по величине из чисел b 1
,b2
,b3
, и где наименьшее из чисел а1
,а2
,а3
находиться над наименьшим из чисел b 1
,b2
,b3
то последовательность одномонотонная.
Если 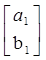 =a1
b1
, и =a1
b1
, и 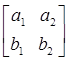 =а1
b1
+а2
b2
, то =а1
b1
+а2
b2
, то 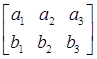 =а1
b1
+а2
b2
+a3
b3 =а1
b1
+а2
b2
+a3
b3
Для доказательства следующих теорем нам понадобится одно свойство одномонотонных последовательностей, которое оформим в виде леммы.
Лемма. Если (а1
, а2
, …а
n
) и (b 1
, b2
,…
bn
) одномонотонные последовательности, то их произведение не изменится при перестановки местами столбцов.
Доказательство.
Рассмотрим последовательность с двумя переменными из двух переменных.
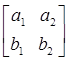 =а1
b1
+а2
b2
. =а1
b1
+а2
b2
.
Заметим, что а1
b1
+а2
b2
= а2
b2
+ а1
b1
по переместительному свойству сложения. Значит, в самой таблице мы тоже можем переставлять столбцы переменных, при этом сохраняется одномонотонность последовательности. То есть
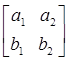 = =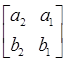
Теперь рассмотрим последовательность с двумя последовательностями из трех переменных.
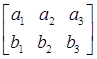 =а1
b1
+а2
b2
+a3
b3
. =а1
b1
+а2
b2
+a3
b3
.
Кроме того, что мы можем поменять переменные по переместительному свойству, а по сочетательному свойству мы можем объединять некоторые слагаемые, сохраняя одномонотонность последовательности. То есть
а1
b1
+а2
b2
+a3
b3
= (a3
b3
+а2
b2
)+ а1
b1
=
Лемма доказана
Теорема 2. Пусть (а1
а2
а3
), (b1
b2
b
3
) – одномонотонные последовательности и (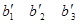 )(
здесь и в дальнейшем) любая перестановка чисел b1
b2
b
3
. Тогда )(
здесь и в дальнейшем) любая перестановка чисел b1
b2
b
3
. Тогда
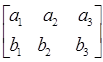 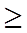 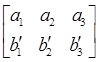 . .
Доказательство.
Действительно, если последовательность 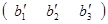 отличается от (b1
b2
b3
) то найдется пара чисел k, l (1 отличается от (b1
b2
b3
) то найдется пара чисел k, l (1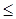 k<l k<l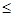 3) такая, что последовательности (ak
, al
) и (bk
, bl
) не одномонотонны. Значит, поменяв местами числа 3) такая, что последовательности (ak
, al
) и (bk
, bl
) не одномонотонны. Значит, поменяв местами числа 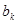 и и 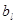 , мы увеличим всю сумму, а значит и всю сумму , мы увеличим всю сумму, а значит и всю сумму 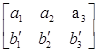 . То есть . То есть
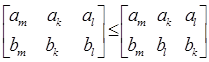 , так как , так как  . .
Очевидно, что за конечное число попарных перестановок элементов 2-ой строки можно получить одномонотонную последовательность.
Теорема доказана
Упражнения
Данные ниже упражнения мы решим с помощью Теоремы 2
Упражнение №1.
Пусть a и b и c – положительные вещественныечисла.
Докажите неравенство.
a3
+b3
+c3
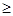 a2
b+b2
c+c2
a. a2
b+b2
c+c2
a.
Доказательство.
Заметим, прежде всего, что
a3
+b3
+c3
= , a2
b+b2
c+c2
a = , a2
b+b2
c+c2
a = 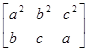
А так как последовательности (a2
, b2
, c2
), (a, b , c) одномонотонны, то
 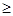 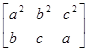 . .
А это значит, что a3
+b3
+c3
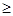 a2
b+b2
c+c2
a. a2
b+b2
c+c2
a.
Что и требовалось доказать.
Упражнение №2.
Пусть a и b и c – положительные вещественныечисла.
Докажите неравенство.
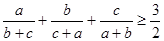 . .
Доказательство.
Заметим, прежде всего, что

и (a, b, c) и (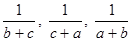 ) одномонотонные последовательности, то ) одномонотонные последовательности, то
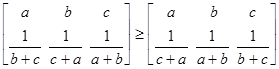 , ,
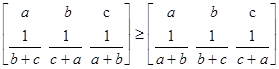 . .
Складывая эти неравенства, мы получаем
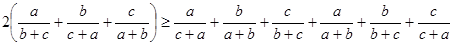 . .
Отделим дроби с одинаковым знаменателем в правой части
 . .
Вычислив, получаем
 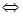 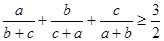 . .
А это значит, что 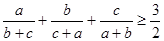
Что и требовалось доказать
2.4 Случай с двумя последовательностями из
n
переменных
Рассмотрим одномонотонные последовательность (а1
, а2
, …аn
) и (b 1
, b2
,…bn
)
Если 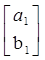 =a1
b1
, и =a1
b1
, и 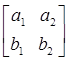 =а1
b1
+а2
b2
, то =а1
b1
+а2
b2
, то 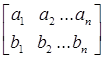 =а1
b1
+а2
b2
…an
bn =а1
b1
+а2
b2
…an
bn
Теорема 3. Пусть (
а1
а2
… аn
), (
b1
b2 …
bn
) – одномонотонные последовательности и (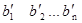 )перестановка чисел b1
b2 …
bn
. Тогда )перестановка чисел b1
b2 …
bn
. Тогда
  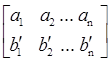 . .
Доказательство.
Действительно, если последовательность (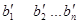 ) отличается от (b1
b2 …
bn
) то найдется пара чисел k, l (1 ) отличается от (b1
b2 …
bn
) то найдется пара чисел k, l (1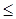 k<l k<l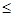 n) такая, что последовательности (ak
, al
) и (bk
, bl
) не одномонотонны. Значит, поменяв местами числа и n) такая, что последовательности (ak
, al
) и (bk
, bl
) не одномонотонны. Значит, поменяв местами числа и 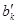 и и 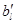 , мы увеличим всю сумму, а значит и всю сумму , мы увеличим всю сумму, а значит и всю сумму 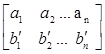 . То есть . То есть
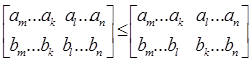 , ,
так как  . .
Очевидно, что за конечное число попарных перестановок элементов 2-ой строки можно получить одномонотонную последовательность.
Теорема доказана.
Следствие.
Для любого n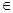 N верно N верно
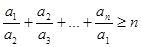 . .
Доказательство.

Но последовательности (а1
а2
… аn
) и (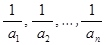 ) не являются одномонотонными, и поэтому мы не можем воспользоваться теоремой 3. ) не являются одномонотонными, и поэтому мы не можем воспользоваться теоремой 3.
Однако эти последовательности противомонотонны: числа в последовательностях расположены в обратном порядке – самому большому по величине соответствует самое маленькое, а самому маленькому соответствует самое большое. А из противомонотонных последовательностей сделать одномонотонные очень просто – достаточно все числа второй линии взять со знаком минус. В данном случае одномонотонными являются последовательности
(а1
а2
… аn
) и ( ) )
Поэтому
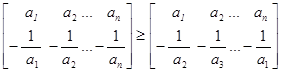
Отсюда и следует искомое неравенство
Следствие
Для любого n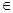 N верно N верно
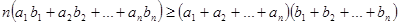
(Неравенство Чебышева).
Доказательство.
В силу теоремы 3 справедливы следующие nнеравенства
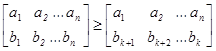
Значит

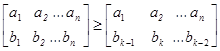
В этих неравенствах левая часть не изменяется, а в правой части элементы второй строки меняются циклически.
Складываем все и получаем
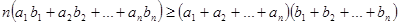
Что и требовалось доказать
Упражнение №1.
Пусть a и b и c – положительные вещественныечисла.
Докажите неравенство.
a3
+b3
+c3
+d3
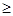 a2
b+b2
c+c2
d+d2
a. a2
b+b2
c+c2
d+d2
a.
Доказательство.
Заметим, прежде всего, что
a3
+b3
+c3
+d3
=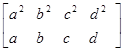 , a2
b+b2
c+c2
d+d2
a= , a2
b+b2
c+c2
d+d2
a=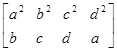 . .
А так как последовательности
(a2
, b2
, c2
, d3
), (a, b , c, d)
одномонотонны, то
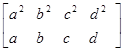 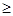 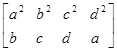 . .
А это значит, что a3
+b3
+c3
+d3
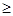 a2
b+b2
c+c2
d+d2
a. a2
b+b2
c+c2
d+d2
a.
Что и требовалось доказать.
Доказательство этого неравенства с помощью одномонотонных последовательностей я не могу сравнить с другим доказательством, так как доказать другим способом это неравенство я не смогла.
2.5 Случай с
n
последовательностями из
n
переменных
Рассмотрим одномонотонные последовательность (а1
, а2
, …аn
), (b1
, b2
,…bn
), …(d1
, d2
,…, dn
).
Если 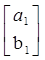 =a1
b1
, и =a1
b1
, и 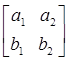 =а1
b1
+а2
b2
, и =а1
b1
+а2
b2
, и 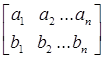 =а1
b1
+а2
b2
…an
bn
, =а1
b1
+а2
b2
…an
bn
,
то 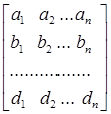 = а1
b1
…d1
+а2
b2
…d2
+ …+an
bn
…dn = а1
b1
…d1
+а2
b2
…d2
+ …+an
bn
…dn
Теорема 4. Рассмотрим одномонотонные последовательности
(а1
, а2
, …аn
), (b 1
, b2
,…bn
), …, (d1
, d2
,…,dn
). Тогда
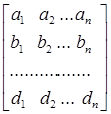  . .
Доказательство.
Действительно, если последовательность (a1
, а2
, …аn
), (b'1
, b'2
,…b'n
), …, (d'1
, d'2
,…,d'n
) отличается от (а1
, а2
, …аn
), (b 1
, b2
,…bn
), …, (d1
, d2
,…,dn
), то найдутся переменные k, l (1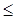 k<l k<l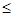 n) такие, что последовательности (ak
, al
) и (bk
, bl
) …(dk
, dl
) не одномонотонны. Значит, поменяв местами числа n) такие, что последовательности (ak
, al
) и (bk
, bl
) …(dk
, dl
) не одномонотонны. Значит, поменяв местами числа 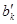 , ,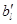 , ak
, al
… dk
, dl
мы увеличим всю сумму, а значит и всю сумму , ak
, al
… dk
, dl
мы увеличим всю сумму, а значит и всю сумму 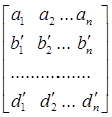 . То . То
есть
 , ,
так как 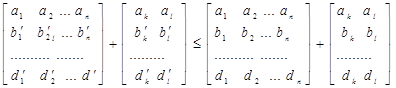 . .
Очевидно, что за конечное число попарных перестановок элементов n-ой строки можно получить одномонотонную последовательность.
Теорема доказана.
Пример
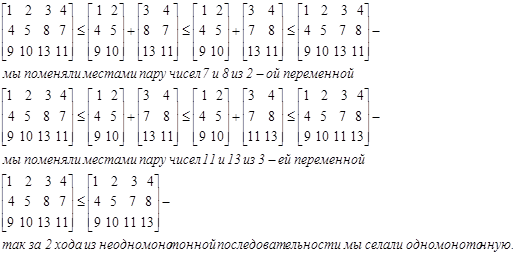
Упражнение 1
Пусть а1
, а2
, …аn
- положительные вещественные числа.
Докажите, что 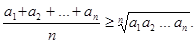
Это неравенство называется неравенством Коши о среднем арифметическом и среднем геометрическом. Докажем его двумя способами
Доказательство.
Перепишем его в виде:
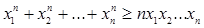 , введя новые переменные , введя новые переменные
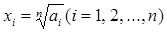
Имеем
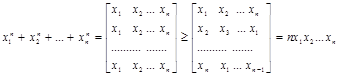

Если сравнить эти два доказательства неравенства, можно заметить, что доказательство с помощью одномонотонных последовательностей гораздо легче в сравнении с доказательством Коши.
неравенство одномонотонный последовательность коши
Заключение
Работая по данной теме, я узнала новый способ доказательства неравенств, вспомнила уже изученные способы доказательства неравенств. Все упражнения в работе я решала сама.
Список использованной литературы
1. Большой справочник школьника. 5 – 11 кл. М. Дрофа, 2001 г.
2. В.В. Зайцев, В.В. Рыжков, М.И. Сканави. Элементарная математика (повторительный курс). М., Наука. 1976 г.
3. Р.Б. Алексеев, Л.Д. Курлядчик. Нетрадиционные способы доказательства традиционных неравенств. /Математика в школе. 1991 г. №4
4. Л. Пинтер, Й. Хегедыш. Упорядоченные наборы чисел и неравенства. /Квант. 1985 г. №12.
|