Задача 1.2
Цех хлебозавода по производству муки заключил контракт с мини-пекарней о поставке ежедневно 300 кг ржаной и пшеничной муки, причем пшеничной - не менее 50%. Зерно, поступающее в цех, проходит в нем обмолот, помол и упаковку муки. Трудозатраты (в человеко-часах) на указанные операции представлены в таблице:
| Операция |
Ржаная мука |
Пшеничная мука |
Имеющийся ресурс |
| Обмолот |
0,1 |
0,1 |
30 |
| Помол |
0,1 |
0,08 |
27 |
| Упаковка |
0,05 |
0,05 |
200 |
Себестоимость одного килограмма ржаной муки составляет 14 рублей, а пшеничной - 18 рублей.
Требуется найти оптимальный план производства продукции, позволяющий цеху выполнить условия контракта с наименьшими затратами.
Решение.
Пусть x1
- объем производства ржаной муки, x2
- объем производства пшеничной муки. Тогда задача может быть описана в виде следующей модели линейного программирования:
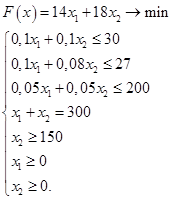
Заполним данные в среде MicrosoftExcel

Добавим в таблицу еще одну строку (например, строку 9 План), в которую будут вноситься получаемые в ходе решения результаты. Объем производства ржаной муки будем предполагать получить в ячейке В9, пшеничной муки - в ячейке С9, а затраты на себестоимость - в ячейке D7.
Для решения задачи необходимо также выделить столбец (в данном примере - столбец D), в который будут введены формулы для расчета значений левой части ограничений. Формула вводится также и в ячейку, в которой будет рассчитаны затраты на себестоимость предприятия (ячейка D7). Нужно обратить внимание на то, что в формулах используются не числа или символьные обозначения, а координаты ячеек таблицы, в которых хранятся эти числа и переменные.
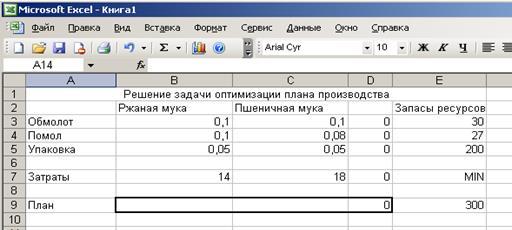
D3= СУММПРОИЗВ(B3:C3;$B$9:$C$9)
D4= СУММПРОИЗВ(B4:C4;$B$9:$C$9)
D5= СУММПРОИЗВ(B5:C5;$B$9:$C$9)
D7= СУММПРОИЗВ(B7:C7;$B$9:$C$9)
D9=B9+C9
Для запуска процедуры оптимизации в меню Сервис необходимо выбрать пункт Поиск решения. В поле Установить целевую ячейку вводятся координаты ячейки (D7), которую необходимо минимизировать.
В поле Изменяя ячейки вводятся координаты ячеек (разделенные запятыми или объединенные в интервал двоеточием), в которых содержатся значения переменных - объемов производства ржаной и пшеничной муки. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. В поле Ограничения необходимо ввести все граничные условия задачи:

При этом ограничения на неотрицательность переменных можно ввести путем установки флажка Неотрицательные значения в окне Параметры. В случае, если решаемая задача является задачей линейного программирования, лучше отметить это в окне Параметры соответствующим флажком:

Запуск процесса оптимизации производится нажатием кнопки Выполнить. По окончании счета появляется диалоговое окно Результаты поиска решения. Нажав в нем соответствующую кнопку, можно сохранить найденное решение или восстановить исходные значения. Изменения при этом коснутся как целевой ячейки, так и влияющих ячеек. В этом же диалоговом окне можно указать необходимые типы отчетов, которые будут размещены на отдельных листах книги.
Отчет Результаты отражает исходные и результирующие значения целевой и влияющих ячеек, а также сведения о наложенных ограничениях.

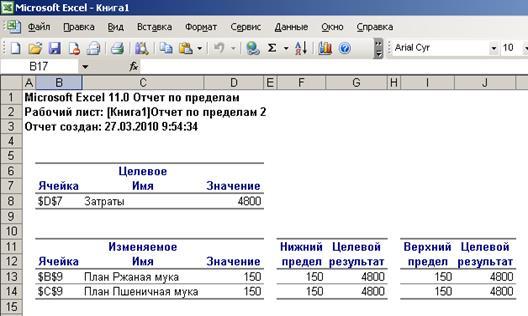
Таким образом предприятию необходимо выпустить 150 кг ржаной муки и 150 кг пшеничной муки, тогда минимальная себестоимость выпуска составит 4800 человеко-часов, при этом ресурсы на обмолот и помол будут использованы полностью, а ресурсы на упаковку останутся в избытке в количестве 185 человеко-часов.
Задача 2.2
Руководство птицефабрики имеет возможность закупать корма трех видов. Из этих кормов птицы должны получать питательные вещества (П1, П2, П3 и П4), требуемое количество которых и содержание в кормах (в ед.) приведены в таблице:
Питательные
вещества
|
Корма |
Нормы потребления |
| К1 |
К2 |
К3 |
| П1 |
3 |
5 |
0 |
равно 16 |
| П2 |
2 |
2 |
4 |
не менее 24 |
| П3 |
8 |
1 |
2 |
не менее 25 |
| П4 |
4 |
3 |
5 |
не менее 33, но не более 40 |
Цены за 1 т кормов составляют соответственно 1000, 900 и 800 рублей.
Какие корма и в каком количестве следует закупать, чтобы затраты птицефабрики оказались минимальными?
Решение.
Решение:
обозначим за x1
количество корма К1, за x2
- количество корма К2, за x3
- количество корма К3. Тогда:

Подготовим в MicrosoftExcel таблицу для решения задачи:

Поскольку MicrosoftExcel позволяет путем установки соответствующего флажка автоматически определять неотрицательность переменных, добавление ограничений на неотрицательность в модель при решении задачи в MicrosoftExcel не является обязательным.
Введем в таблицу формулы для расчета левых частей ограничений и целевой ячейки:
Е4= СУММПРОИЗВ(B4:D4;$B$12:$D$12)
Е5=СУММПРОИЗВ(B5:D5;$B$12:$D$12)
Е6=СУММПРОИЗВ(B6:D6;$B$12:$D$12)
Е7=СУММПРОИЗВ(B7:D7;$B$12:$D$12)
Е8=СУММПРОИЗВ(B8:D8;$B$12:$D$12)
Целевая ячейка Е10=СУММПРОИЗВ(B10:D10;$B$12:$D$12)
Ограничения запишутся так
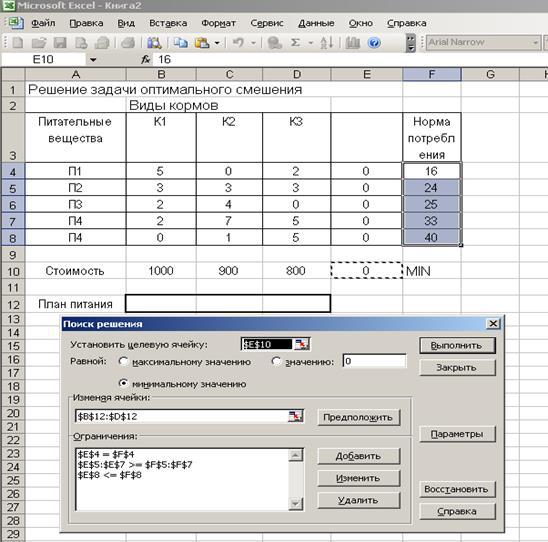
Запустим модуль Поиск решения и произведем расчеты

В ходе расчетов получим следующие результаты: оптимальный рацион должен содержать 3,125 ед. корма К1, 4,6875 ед. корма К2 и 0,1875 корма К3. При этом стоимость рациона будет составлять 7493,75 руб.
Задача 3.1
Один из цехов фабрики по пошиву изделий из кожи раскраивает поступающие заготовки для получения 5 видов деталей одним из трех возможных способов. Из одной заготовки получают:
| Способ раскроя |
Детали |
| A |
B |
C |
D |
E |
| I |
10 |
5 |
3 |
7 |
2 |
| II |
6 |
8 |
4 |
5 |
2 |
| III |
4 |
7 |
5 |
3 |
4 |
Требуется получить не менее 48 деталей вида А, не менее 32 деталей вида В, не менее 45 деталей вида С, не менее 17 деталей вида D и не менее 24 деталей вида Е.
Какое минимальное количество заготовок нужно раскроить?
Решение.
Обозначим за x1
количество заготовок, разрезаемых по способу 1, за x2
- количество заготовок, разрезаемых по способу 2 и т.д.Используя модель линейного программирования с минимизацией расхода материала, получим:
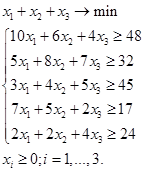
Подготовим таблицу в Microsoft Excel, содержащую исходные данные задачи, введем формулы для расчета целевой функции и левой части ограничений, заполним форму модуля Поиск решения:



Решение
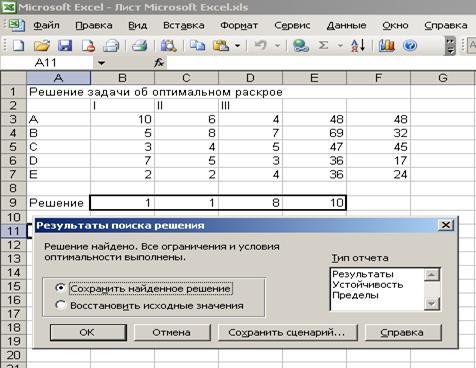
Таким образом, необходимо раскроить 1 заготовку способом I, 1 заготовку способом II, 8 заготовок способом III.
Задача 4.2
Гражданин О. Бендер хочет приобрести некий мебельный гарнитур, стоимость которого 100 тыс. рублей. Администрация аукциона согласна на выплату в рассрочку, с условием, что 20 тыс. руб. О. Бендер выплатит через 2 месяца, а остальную сумму - через 4 месяца.
Однако О. Бендер, справедливо полагая, что найти требуемую сумму ему не удастся, хочет получить средства путем вложения денег по одному из типов вклада: А (сроком на 1 месяц под 1,5%), В (сроком на 2 месяца под 3,5%) или С (сроком на 4 месяца под 8%).
Какую сумму и по какому типу вклада нужно вложить О. Бендеру, чтобы через 4 месяца купить гарнитур?
| Тип вклада |
Срок вклада (мес.) |
Процент по вкладу |
| A |
1 |
1,5 |
| B |
2 |
3,5 |
| C |
4 |
8,0 |
Необходимо минимизировать размер целевого фонда.
Решение:
Составим таблицу, отражающую возможности вложения и возврата денег по месяцам:
| Вклады |
1 |
2 |
3 |
4 |
5 |
| A1 |
1®® |
1,015 |
| A2 |
1®® |
1,015 |
| A3 |
1® |
1,015 |
| A4 |
1®® |
1,015 |
| B1 |
1®® |
®®® |
1,035 |
| B3 |
1®® |
®®® |
1,035 |
| C1 |
1®® |
®®® |
®®® |
®®® |
1,08 |
где: Ai - размер вклада типа A в месяце i; Bi - размер вклада типа B в месяце i; Ci - размер вклада типа C в месяце i;
Задача может быть описана следующей моделью:


Функция minimize
возвращает вектор значений переменных, являющихся аргументами целевой функции, при которых ее значение будет минимальным. В первой колонке – порядковый номер переменной, начиная с нулевого, по очередности упоминания. Во второй – соответствующие значения переменных.
При необходимости, присвоив переменным полученные значения, можно рассчитать и значение целевой функции.
Задача 5.2
Четыре фермерских хозяйства, находящиеся в Рязанской, Владимирской, Тверской и Смоленской областях, направляют выращиваемые овощи и фрукты на переработку и консервацию на один из трех заводов, которые расположены в Москве, Туле и Ярославле.
Затраты на перевозку 1 т продукции представлены в таблице (в рублях):
| Москва |
Тула |
Ярославль |
| Рязанское |
500 |
700 |
800 |
| Владимирское |
400 |
800 |
300 |
| Тверское |
400 |
700 |
400 |
| Смоленское |
600 |
600 |
700 |
В сезон Рязанское хозяйство производит 40 т продукции в неделю, Владимирское - 50 т, Тверское - 60 т, Смоленское - 70 т, в то время как завод в Москве может переработать в неделю 100 т продукции, в Туле - 50 т, в Ярославле - 40 т.
Составьте план перевозок продукции из фермерских хозяйств на заводы с минимальными транспортными расходами, учитывая, что в связи с ремонтом трассы Москва-Рязань в неделю по ней можно перевезти не более 20 т продукции.
Решение:
В данной задаче количество выращиваемых продуктов, на 30 т больше, чем могут переработать заводы. Сведем задачу к замкнутому виду, добавив фиктивного пятого поставщика.
Модель рассматриваемой задачи выглядит так:
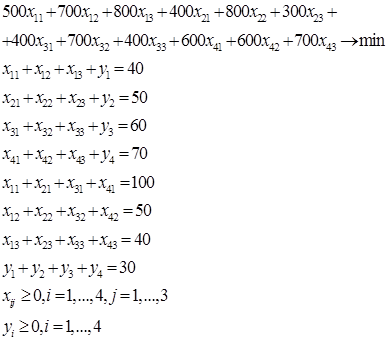
Заметим, что в целевую функцию не введены штрафы за нереализацию продукции в связи с их отсутствием в условии задачи.
Для того, чтобы удовлетворить требованию  вместо Московского завода введем двух других. вместо Московского завода введем двух других.
Один из них, под именем Московского завода будет иметь потребности, то есть возможности в переработке в количестве 20 т и с теми же стоимостями перевозок, а второй с возможностью 100 – 20 = 80 и с теми же стоимостями перевозок, за исключением с15
, которую примем равной сколь угодно большому числу, например, 1000000000.
После нахождения оптимального плана объемы перевозок в Москву необходимо прибавить к объемам перевозок Потребителя 2
В результате исходная задача примет вид
| Москва |
Тула |
Ярославль |
Потребитель 1 |
Потребитель 2 |
Ресурсы |
| Рязанское |
500 |
700 |
800 |
0 |
10000000000 |
40 |
| Владимирское |
400 |
800 |
300 |
0 |
400 |
50 |
| Тверское |
400 |
700 |
400 |
0 |
400 |
60 |
| Смоленское |
600 |
600 |
700 |
0 |
600 |
70 |
| Потребности |
20 |
50 |
40 |
30 |
80 |
220 |
Решим задачу при помощи модуля Поиск решения:

Целевая ячейка D19 =СУММПРОИЗВ(B2:F5;B12:F15)


Получаемрешение

С учетом ограничений на трассу Москва-Рязань окончательно получаем план перевозок
| Москва |
Тула |
Ярославль |
| Рязанское |
20 |
0 |
0 |
| Владимирское |
10 |
0 |
40 |
| Тверское |
60 |
0 |
0 |
| Смоленское |
10 |
50 |
0 |
И окончательную стоимость
20*500+10*400+60*400+10*600+50*600+40*300 = 86000 у.е.
Задача 6.2
Фирма получила заказ на срочный перевод четырех книг с итальянского языка. Фирма может располагать услугами 5 переводчиков, способных выполнить работу такого уровня. Время в днях, за которое каждый переводчик справится с работой, приведено в таблице:
| Книга 1 |
Книга 2 |
Книга 3 |
Книга 4 |
| Иванов |
10 |
25 |
14 |
25 |
| Петров |
8 |
12 |
16 |
28 |
| Сидоров |
12 |
18 |
17 |
33 |
| Андреев |
14 |
23 |
15 |
30 |
| Васильев |
11 |
20 |
18 |
28 |
Фирма использует повременную оплату труда. Переводчики имеют разную квалификацию, поэтому за день работы фирма платит Иванову 700 рублей в день, Петрову - 800 рублей в день, Сидорову - 600, Андрееву - 500, Васильеву - 550. Поскольку по оценке фирмы качество переводов в итоге будет примерно одинаковым, руководство фирмы просит Вас составить такое распределение работ, которое позволит минимизировать затраты на переводы.
Решение.
Составим модель линейного программирования, отражающую условие:

Решим задачу при помощи MicrosoftExcel:

При решении задач о назначении особый интерес вызывает способ ввода ограничений при заполнении формы модуля Поиск решения и формулы целевой функции:
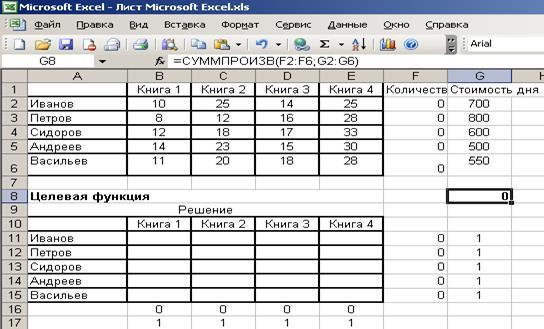


Проведенные расчеты показывают, что минимальное общие затраты на перевод составили 48800 рублей. Назначение переводчика для перевода книги определяется наличием на пересечении строки и столбца значения 1.
Книгу 1 — Петров
Книгу 2 — Иванов
Книгу 3 — Васильев
Книгу 4 — Андреев
|