| КУРСОВА РОБОТА
На тему
«Моделювання оптимальної стратегії заміни обладнання за допомогою динамічного програмування»
Суми – 2006
Вступ
У наш час наука приділяє велику увагу питанням організацій й керування, це приводить до необхідності аналізу складних цілеспрямованих процесів під кутом зору їхньої структури й організації. Потреби практики викликали до життя спеціальні методи, які зручно поєднувати за назвою «дослідження операцій». Під цим терміном розуміється застосування математичних, кількісних методів для обґрунтування рішень у всіх областях цілеспрямованої людської діяльності.
Метою динамічного програмування є визначення найкращого способу дії при рішенні того або іншого завдання. Для побудови математичної моделі необхідно мати строге подання про мету функціонування досліджуваної системи й мати інформацію про обмеження, які визначають область припустимих значень. Мета й обмеження повинні бути представлені у вигляді функцій.
Практично всі методи динамічного програмування породжують алгоритми, які є ітераційними по своїй природі. Це має на увазі, що завдання вирішується послідовно (ітераціонно), коли на кожному кроці (ітерації) одержуємо рішення, що поступово сходяться до оптимального рішення.
Ітераційна природа алгоритмів звичайно приводить до об'ємних однотипних обчислень. У цьому й полягає причина того, що ці алгоритми розробляються, в основному, для реалізації за допомогою обчислювальної техніки.
Метою даної курсової роботи є знаходження оптимального плану заміни обладнання для максимізації прибутковості діяльності підприємства.
Об’єктом курсової роботи виступає будь-яке підприємство яке має устаткування та обладнання, що використовує для виготовлення продукції.
Предметом курсової роботи являється методи динамічного програмування.
1. Теоретичні відомості щодо динамічного програмування
Більшість методів дослідження операцій зв'язано в першу чергу із завданнями цілком певного змісту. Класичний апарат математики виявився малопридатним для рішення багатьох завдань оптимізації, що включають велике число змінних й/або обмежень у вигляді нерівностей. Безсумнівна привабливість ідеї розбивки завдання великої розмірності на підзадачі меншої розмірності, що включають усього по декількох змінних, і наступного рішення загального завдання вроздріб. Саме на цій ідеї заснований метод динамічного програмування.
Динамічне програмування (ДП) являє собою математичний метод, заслуга створення й розвитку якого належить насамперед Беллману. Метод можна використати для рішення досить широкого кола завдань, включаючи завдання розподілу ресурсів, заміни й керування запасами, завдання про завантаження. Характерним для динамічного програмування є підхід до рішення завдання по етапах, з кожним з яких асоційована одна керована змінна. Набір рекурентних обчислювальних процедур, що зв'язують різні етапи, забезпечує одержання припустимого оптимального рішення завдання в цілому при досягненні останнього етапу.
Походження назви динамічне програмування, імовірно, пов'язане з використанням методів ДП у завданнях прийняття рішень через фіксовані проміжки часу (наприклад, у завданнях керування запасами). Однак методи ДП успішно застосовуються також для рішення завдань, у яких фактор часу не враховується. Із цієї причини більше вдалим представляється термін багатоетапне програмування, що відбиває покроковий характер процесу рішення завдання.
Фундаментальним принципом, покладеним в основу теорії ДП, є принцип оптимальності. Власне кажучи, він визначає порядок поетапного рішення завдання, що допускає декомпозицію, (це більше прийнятний шлях, чим безпосереднє рішення завдання у вихідній постановці) за допомогою рекурентних обчислювальних процедур.
Динамічне програмування дозволяє здійснювати оптимальне планування керованих процесів. Під «керованими» розуміються процеси, на хід яких ми можемо в тім або іншому ступені впливати.
Нехай передбачається до здійснення деякий захід або серія заходів («операція»), що переслідує певну мету. Запитується: як потрібно організувати (спланувати) операцію для того, щоб вона була найбільш ефективною? Для того, щоб поставлене завдання придбало кількісний, математичний характер, необхідно ввести в розгляд деякий чисельний критерій W, яким ми будемо характеризувати якість, успішність, ефективність операції. Критерій ефективності в кожному конкретному випадки вибирається виходячи із цільової спрямованості операції й завдання дослідження (який елемент керування оптимізується й для чого).
Сформулюємо загальний принцип, що лежить в основі рішення всіх завдань динамічного програмування («принцип оптимальності»):
«Який би не був стан системи S перед черговим кроком, треба вибрати керування на цьому кроці так, щоб виграш на даному кроці плюс оптимальний виграш на всіх наступних кроках був максимальним».
Динамічне програмування – це поетапне планування багатокрокового процесу, при якому на кожному етапі оптимізується тільки один крок. Керування на кожному кроці повинне вибиратися з обліком всіх його наслідків у майбутньому.
При постановці завдань динамічного програмування варто керуватися наступними засадами:
– вибрати параметри (фазові координати), що характеризують стан S керованої системи перед кожним кроком;
– розчленувати операцію на етапи (кроки);
– з'ясувати набір крокових керувань xі
для кожного кроку й обмеження, що накладають на них;
– визначити який виграш приносить на і-ом кроці керування xі
, якщо перед цим система могла S, тобто записати «функцію виграшу»;
– визначити, як змінюється стан S системи S під впливом керування xі
на і-ом кроці: воно переходить у новий стан;
– записати основне рекурентне рівняння динамічного програмування, що виражає умовний оптимальний виграш Wі
(S) (починаючи з і-го кроку й до кінця) через уже відому функцію Wі
+1 (S).
Цьому виграшу відповідає умовне оптимальне керування на і-м кроці xі(S) (причому у вже відому функцію Wі
+1 (S) треба замість S підставити змінений стан).
– зробити умовну оптимізацію останнього (m-го) кроку, задаючись гамою станів S, з яких можна за один крок дійти до кінцевого стану, обчислюючи для кожного з них умовний оптимальний виграш по формулі.
– зробити умовну оптимізацію (m-1) – го, (m-2) – го й т.д. кроків по формулі, думаючи в ній й=(m-1), (m-2),…, і для кожного із кроків указати умовне оптимальне керування xі
(S), при якому максимум досягається.
Помітимо, що якщо стан системи в початковий момент відомо (а це звичайно буває так), те на першому кроці варіювати стан системи не потрібно – прямо знаходимо оптимальний виграш для даного початкового стану S0
. Це і є оптимальний виграш за всю операцію.
– зробити безумовну оптимізацію керування, «читаючи» відповідні рекомендації на кожному кроці. Взяти знайдене оптимальне керування на першому кроці; змінити стан системи по формулі; для знову знайденого стану знайти оптимальне керування на другому кроці х2
* і т.д. до кінця.
У завданнях динамічного програмування економічний процес залежить від часу (від декількох періодів (етапів) часу), тому перебуває ряд оптимальних рішень (послідовно для кожного етапу), що забезпечують оптимальний розвиток усього процесу в цілому. Завдання динамічного програмування називаються багатоетапними або багатокроковими. Динамічне програмування являє собою математичний апарат, що дозволяє здійснювати оптимальне планування багатокрокових керованих процесів і процесів, що залежать від часу. Економічний процес називається керованим, якщо можна впливати на хід його розвитку. Керуванням називається сукупність рішень, прийнятих на кожному етапі для впливу на хід процесу. В економічних процесах керування полягає в розподілі й перерозподілі засобів на кожному етапі. Наприклад, випуск продукції будь-яким підприємством – керований процес, тому що він визначається зміною складу встаткування, обсягом поставок сировини, величиною фінансування й т.д. Сукупність рішень, прийнятих на початку кожного року планованого періоду по забезпеченню підприємства сировиною, заміні встаткування, розмірам фінансування й т.д., є керуванням. Здавалося б, для одержання максимального обсягу випускає продукції, що, найпростіше вкласти максимально можлива кількість засобів і використати на повну потужність устаткування. Але це привело б до швидкого зношування встаткування й, як наслідок, до зменшення випуску продукції. Отже, випуск продукції треба спланувати так, щоб уникнути небажаних ефектів. Необхідно передбачити заходи, що забезпечують поповнення встаткування в міру зношування, тобто по періодах часу. Останнє хоча й приводить до зменшення первісного обсягу випускає продукції, що, але забезпечує надалі можливість розширення виробництва. Таким чином, економічний процес випуску продукції можна вважати складається з декількох етапів (кроків), на кожному з яких здійснюється вплив на його розвиток.
Початком етапу (кроку) керованого процесу вважається момент ухвалення рішення (про величину капітальних вкладень, про заміну встаткування певного виду й т.д.). Під етапом звичайно розуміють господарський рік.
Динамічне програмування, використовуючи поетапне планування, дозволяє не тільки спростити рішення завдання, але й вирішити ті з них, до яких не можна застосувати методи математичного аналізу. Спрощення рішення досягається за рахунок значного зменшення кількості досліджуваних варіантів, тому що замість того, щоб один раз вирішувати складне різноманітне завдання, метод поетапного планування припускає багаторазове рішення щодо простих завдань.
Плануючи поетапний процес, виходять із інтересів усього процесу в цілому, тобто при ухваленні рішення на окремому етапі завжди необхідно мати у виді кінцеву мету.
Однак динамічне програмування має й свої недоліки. На відміну від лінійного програмування, у якому симплексний метод є універсальним, у динамічному програмуванні такого методу не існує. Кожне завдання має свої труднощі, і в кожному випадку необхідно знайти найбільш підходящу методику рішення. Недолік динамічного програмування полягає також у трудомісткості рішення багатомірних завдань. При дуже великому числі змінних рішення завдання навіть на сучасних ЕОМ обмежується пам'яттю й швидкодією машини. Наприклад, якщо для дослідження кожного змінного одномірного завдання потрібно 10 кроків, то у двовимірному завданні їхня кількість збільшується до 100, у тривимірної – до 1000 і т.д.
Припустимо, якась система S перебуває в деякому початковому стані S0
й є керованою. Таким чином, завдяки здійсненню деякого керування U зазначена система переходить із початкового стану S0
у кінцевий стан Sк
. При цьому якість кожного з реалізованих керувань U характеризується відповідним значенням функції W(U)
. Завдання полягає в тім, щоб з безлічі можливих керувань U знайти таке U*, при якому функція W(U)
приймає екстремальне (максимальне або мінімальне) значення W(U*)
.
Завдання динамічного програмування мають геометричну інтерпретацію. Стан фізичної системи S можна описати числовими параметрами, наприклад витратою пального й швидкістю, кількістю вкладених коштів і т.д. Назвемо ці параметри координатами системи; тоді стан системи можна зобразити крапкою S, а перехід з одного стану S1 в інше S2 – траєкторією крапки S. Керування U означає вибір певної траєкторії переміщення крапки S з S1 в S2, тобто встановлення певного закону руху крапки S.
Сукупність станів, у які може переходити система, називається областю можливих станів. Залежно від числа параметрів, що характеризують стан системи, область можливих станів системи може бути різної. Нехай, наприклад, стан системи S характеризується одним параметром, – координатою x. У цьому випадку зміна координати, якщо на неї накладені деякі обмеження, зобразиться переміщенням крапки S по осі Оx
або по її ділянці. Отже, областю можливих станів системи є сукупність значень x, а керуванням – закон руху крапки S з початкового стану S0 у кінцеве Sk
по осі Ox
або її частини (рис. 1.1).
    S0
S Sk S0
S Sk
  0 x 0 x
Область можливих станів системи
Рисунок 1.1. Графічне зображення переходу системи S
Таким чином, завданню динамічного програмування можна дати наступну геометричну інтерпретацію. Із всіх траєкторій, що належать області можливих станів системи й з'єднуючих областей S0
й Sk
, необхідно вибрати таку, на якій критерій W приймає оптимальне значення.
Щоб розглянути загальне рішення завдань динамічного програмування, уведемо позначення й зробимо для подальших викладів припущення.
Будемо вважати, що стан розглянутої системи S на K-м кроці (k=1, n) визначається сукупністю чисел X(k)
=(x1
(k)
, x2
(k)
,…, xn
(k)
), які отримані в результаті реалізації керування uk, що забезпечило перехід системи S зі стану X(k-1)
у стан X(k)
. При цьому будемо припускати, що стан X(k)
, у яке перейшла система S, залежить від даного стану X(k-1)
і обраного керування uk
і не залежить від того, яким образом система S прийшла в стан X(k-1)
.
Далі із уважати, що якщо в результаті реалізації k-го кроку забезпечені певний доход або виграш, що також залежить від вихідного стану системи X(k-1)
і обраного керування uk
і рівний Wk
(X(k-1), uk)
, те загальний доход або виграш за n кроків становить
n
F=∑ Wk
(X(
k
-1)
, uk
)
(1.1)
k=1
Таким чином, завдання динамічного програмування повинна задовольняти дві умови. Першу умову звичайно називають умовою відсутності післядії, а друге – умовою адитивності цільової функції завдання.
Виконання для завдання динамічного програмування першої умови дозволяє сформулювати для неї принцип оптимальності Беллмана. Перш ніж зробити це, треба дати визначення оптимальної стратегії керування. Під такою стратегією розуміється сукупність керувань U*
=(u1
*, u2
*,…, un
*), у результаті реалізації яких система S за n кроків переходить із початкового стану X(0)
у кінцеве X(k)
і при цьому функція (1.1) приймає найбільше значення.
Принцип оптимальності: яке б не був стан системи перед черговим кроком, треба вибрати керування на цьому кроці так, щоб виграш на даному кроці плюс оптимальний виграш на всіх наступних кроках був максимальним.
Звідси треба, що оптимальну стратегію керування можна одержати, якщо спочатку знайти оптимальну стратегію керування на n-м кроці, потім на двох останніх кроках, потім на трьох останніх кроках і т.д., аж до першого кроку. Таким чином, рішення розглянутого завдання динамічного програмування доцільно починати з визначення оптимального рішення на останньому, n-м кроці. Для того щоб знайти це рішення, мабуть, потрібно зробити різні припущення про те, як міг скінчитися передостанній крок, і з обліком цього вибрати керування un0, що забезпечує максимальне значення функції Wn
(X(n-1)
, un
). Таке керування un0 обране при певних припущеннях про те, як скінчиться попередній крок, називається умовно оптимальним керуванням. Отже, принцип оптимальності вимагає знаходити на кожному кроці умовно оптимальне керування для кожного з можливих варіантів попереднього кроку.
Щоб це можна було здійснити практично, необхідно дати математичне формулювання принципу оптимальності. Для цього введемо деякі додаткові позначення. Позначимо через Fn
(X0
) максимальний доход, одержуваний за n кроків при переході системи S з початкового стану X(0)
у кінцевий стан X(k)
при реалізації оптимальної стратегії керування U=(u1
, u2
,…, un
), а через Fn-k
(X(k)
) – максимальний доход, одержуваний при переході з будь-якого стану X(k) у кінцевий стан X(n)
при оптимальній стратегії керування на що залишилися n-k кроках. Тоді:
Fn
(X0
)=max[W1
(X(0)
, u1
)+ … + Wn
(X(
n
-1)
, un
)] (1.2)
Uk
+
j
Fn
-
k
(X(
k
)
)=max[Wk
+1
(X(
k
)
, uk
+1
)+Fn
-
k
-1
(Xk
+1)
)] (k=0, n-1) (1.3)
Uk
+1
Останнє вираження являє собою математичний запис принципу оптимальності й зветься основного функціонального рівняння Беллмана або рекуррентного співвідношення. Використовуючи дане рівняння можна знайти рішення завдання динамічного програмування.
Думаючи k=n-1 у рекуррентном співвідношенні (1.3), одержимо наступне функціональне рівняння:
F1
(X(n-1)
=max[Wn
(X(n-1)
, un
)+F0
(X(n)
)] (1.4)
un
У цьому рівнянні F0
(X(n)
) будемо вважати відомим. Використовуючи тепер рівняння (1.4) і розглядаючи всілякі припустимі із системи S на (n-1) – м кроці X1
(n-1)
, X2
(n-1)
,…, Xm
(n-1)
,…, знаходимо умовні оптимальні рішення un
0
(x1
(
n
-1)
), un
0
(x2
(
n
-1)
),…, un
0
(xm
(
n
-1)
),…
і відповідні значення функції (1.4)
F1
0
(X1
(
n
-1)
), F1
0
(X2
(
n
-1)
), …, F1
0
(Xm
(
n
-1)
),…
Таким чином, на n-м кроці знаходимо умовно оптимальне керування при будь-якому припустимому стані системи S після (n-1) – го кроку. Тобто, у якому би стані система не виявилася після (n-1) – го кроку, буде відомо, яке варто прийняти рішення на n-м кроці. Відомо також і відповідне значення функції (2.4). Розглянемо функціональне рівняння при k=n-2:
F2
(X(n-1)
)=max[Wn-1
(X(n-2)
, un-1
)+F1
(X(n-1)
)] (1.5)
Un
-1
Для того щоб знайти значення F2
для всіх припустимих значень X(n-2),
необхідно знати Wn-1
(X(n-2),
un-1
) і F1
(X(n-1)
). Що стосується значень F1
(X(n-1)
), те вони вже визначені. Тому потрібно зробити обчислення для Wn-1
(X(n-2)
, un-1
) при деякому відборі припустимих значень X(n-2)
і відповідних керувань un-1
. Ці обчислення дозволять визначити умовно оптимальне керування u0n-1 для кожного X(n-2)
. Кожне з таких керувань разом із уже обраним керуванням на останньому кроці забезпечує максимальне значення доходу на двох останніх кроках.
Послідовно здійснюючи описаний вище ітераційний процес, дійдемо до першого кроку. На цьому кроці відомо, у якому стані може перебувати система. Тому вже не потрібно робити припущень про припустимі стани системи, а залишається як тільки вибрати керування, що є найкращим з обліком умовно оптимальних керувань, уже прийнятих на всіх наступних кроках.
Таким чином, у результаті послідовного проходження всіх етапів від кінця до початку визначається максимальне значення виграшу за n кроків і для кожного з них знаходимо умовно оптимальне керування.
Щоб знайти оптимальну стратегію керування, тобто визначити шукане рішення завдання, потрібно тепер пройти всю послідовність кроків, тільки цього разу від початку до кінця. А саме: на першому кроці як оптимальне керування u1
* візьмемо знайдене умовно оптимальне керування u1
0
. На другому кроці знайдемо стан X1
*, у яке переводить систему керування u1
*. Цей стан визначає знайдене умовно оптимальне u2
0
, що тепер уважається оптимальним. Знаючи u2
*, знаходимо X2
*, а виходить, визначаємо u3
* і т.д. У результаті цього найдеться рішення завдання, тобто максимально можливий доход й оптимальну стратегію керування U*, що включає оптимальні керування на окремих кроках: U*= (u1
*, u2
*,…, un
*).
Отже, зі знаходження рішення завдання динамічного програмування видно, що цей процес є досить громіздким. Тому більше складні завдання вирішують за допомогою ЕОМ.
Динамічне завдання по заміні встаткування можливо також вирішити й графічним методом. На осі Х відкладають номер кроку (к). на осі В – вік устаткування (t). Крапка (до-1; t) на площині відповідає початку К-ого кроку по експлуатації встаткування у віці t років.
 Будь-яка траєкторія переводящая крапку S (k-1; t) зі стану S0 S. Складається з відрізків, тобто із кроків відповідним рокам експлуатації. Потрібно вибрати таку траєкторію при якій витрати на експлуатацію будуть мінімальні. Якщо відомі залежність продуктивності встановленого на підприємстві встаткування від часу його використання R(t) і залежність витрат на ремонт устаткування при різному часі його використання S(t) і витрати пов'язані із придбанням нового обладнання, то показником ефективності в цьому випадку є прибуток яка максимізується. Будь-яка траєкторія переводящая крапку S (k-1; t) зі стану S0 S. Складається з відрізків, тобто із кроків відповідним рокам експлуатації. Потрібно вибрати таку траєкторію при якій витрати на експлуатацію будуть мінімальні. Якщо відомі залежність продуктивності встановленого на підприємстві встаткування від часу його використання R(t) і залежність витрат на ремонт устаткування при різному часі його використання S(t) і витрати пов'язані із придбанням нового обладнання, то показником ефективності в цьому випадку є прибуток яка максимізується.
2. Застосування динамічного програмування в економічних дослідженнях
програмування економічний дослідження динамічний
В економічних дослідженнях здавна застосовувалися найпростіші математичні методи. У господарському житті широко використаються геометричні формули. Так, площа ділянки поля визначається шляхом перемножування довжини на ширину або обсяг силосної траншеї – перемножуванням довжини на середню ширину й глибину. Існує цілий ряд формул і таблиць, що полегшують господарським працівникам визначення тих або інших величин.
Застосування арифметики, алгебри в економічних дослідженнях, є вже питанням про культуру дослідження, кожен поважаючий себе економіст володіє такими навичками. Особняком тут стоять так звані методи оптимізації, частіше називаються як економіко-математичні методи.
В 60-і роки нашого сторіччя розгорнулася дискусія про математичні методи в економіці. Наприклад, академік Немчинов виділяв п'ять базових методів дослідження при плануванні:
1) балансовий метод;
2) метод математичного моделювання;
3) векторно-матричний метод;
4) метод економіко-математичних множників (оптимальних суспільних оцінок);
5) метод послідовного наближення.
У той же час академік Канторович виділяв математичні методи в чотири групи:
– макроекономічні моделі, куди відносив балансовий метод і моделі попиту;
– моделі взаємодії економічних підрозділів (на основі теорії ігор);
– лінійне моделювання, включаючи ряд завдань, що небагато відрізняються від класичного лінійного програмування;
– моделі оптимізації, що виходять за межі лінійного моделювання (динамічне, нелінійне, ціле і стохастичне програмування).
І з тієї, і з іншою класифікацією можна сперечатися, оскільки, наприклад моделі попиту можна по ряду особливостей віднести до нелінійного програмування, а стохастичне моделювання йде коріннями в теорію ігор. Але все це проблеми класифікації, які мають певне методологічне значення, але в цьому випадку не настільки важливі.
Із крапки ж зору ролі математичних методів варто говорити лише про широту застосування різних методів у реальних процесах планування.
Із цього погляду безсумнівним лідером є метод лінійної оптимізації, що був розроблений академіком Канторовичем в 30-і роки ХХ-го століття. Найчастіше завдання лінійного програмування застосовується при моделюванні організації виробництва. От як по Канторовичу виглядає математична модель організації виробництва:
У виробництві беруть участь M різних виробничих факторів (інгредієнтів) – робоча сила, сировина, матеріали, устаткування, кінцеві й проміжні продукти й ін. Виробництво використає S технологічних способів виробництва, причому для кожного з них задані обсяги вироблених інгредієнтів, розраховані на реалізацію цього способу з одиничною ефективністю, тобто заданий вектор ak
= (a1k
, a2k
,…, amk
), k = 1,2…, S, у якому кожна з компонентів aіk
указує обсяг виробництва, що відповідає (і-го) інгредієнта, якщо вона позитивна; і обсяг його витрати, якщо вона негативна (у способі k).
Вибір плану означає вказівка інтенсивності використання різних технологічних способів, тобто план визначається вектором x = (x1, x2,…, x) з невід’ємними компонентами.
Звичайно на кількості що випускають і затрачуваних інгредієнтів накладаються обмеження: зробити потрібно не менш, ніж потрібно, а затрачати не більше, ніж є. Такі обмеження записуються у вигляді
S a ik
xk
> bi
; i=1,2,…, m. (2.1)
Якщо і > 0, то нерівність означає, що з потреба в інгредієнті в розмірі й, якщо і < 0, то нерівність означає, що є ресурс даного інгредієнтів розмірі – і =| і |. Далі передбачається, що використання кожного способу, пов'язаного з витратами одного з перерахованих інгредієнтів або особливо виділеного інгредієнта в кількості Ck при одиничній інтенсивності способу k. Як цільова функція приймається сумарна витрата цього інгредієнта в плані.
f(x) = S ck
xk
. (2.2)
Тепер загальне завдання лінійного програмування може бути представлена в математичній формі.
На основі об'єктивно обумовлених оцінок американським математиком Дж. Данцигом – був розроблений симплекс-метод рішення завдань оптимального програмування. Цей метод досить широко застосовується. Алгоритм його досить детально пророблений, і навіть розроблені прикладні пакети програм, які застосовуються в багатьох галузях планування.
Метод лінійної оптимізації з того моменту, як він був розроблений Канторовичем, не залишався без змін, він розвивався й продовжує розвиватися. Наприклад, формула (2.2) у сучасній інтерпретації виглядає в такий спосіб.
S aij
xj
< bi
(i Î I) (2.3)
Аналогічно й з ресурсами, в обмеженні беруть участь не всі ресурси відразу, а якась їхня підмножина (і Î І).
Введенням підмножин не обмежилося вдосконалювання методу лінійної оптимізації. Потреби практики змусили розробити ще цілий ряд прийомів і методів для різних випадків опису реалій господарської практики у вигляді обмежень. Це такі прийоми, як запис обмежень по використанню виробничих ресурсів, запис обмежень по гарантованому обсязі робіт або виробництва продукції, прийоми моделювання при невідомих значеннях показників і багато хто інші, на яких тут не варто зупинятися.
Ціль всіх цих прийомів – дати більше розгорнуту модель якого-небудь явища з господарської практики, заощадивши при цьому на кількості змінних й обмежень.
Незважаючи на широту застосування методу лінійного програмування, він ураховує лише три особливості економічних завдань – велика кількість змінних, обмеженість ресурсів і необхідність цільової функції. Звичайно, багато завдань із іншими особливостями можна звести до лінійної оптимізації, але це не дає нам права випустити з уваги інший добре розроблений метод математичного моделювання – динамічне програмування. По суті, завдання динамічного програмування є описом багатокрокових дій із прийняття рішень. Завдання динамічного програмування можна сформулювати в такий спосіб:
є деяка кількість ресурсу х, яких можна використати N різними способами. Якщо позначити через хі кількість ресурсу, використовувана й-m способом, то кожному способу зіставляється функція корисності (хі), що виражає доход від цього способу. Передбачається, що всі доходи виміряються в однакових одиницях і загальному доході дорівнює сумі доходів, отриманих від використання кожного способу.
Тепер можна поставити завдання в математичній формі. Знайти
max y1
(x1
)+ y2
(x2
)+ … + yn
(xn
) (2.4)
(загальний доход від використання ресурсів всіма способами) при умовах:
– виділювані кількості ресурсів ненегативні;
[1] x1 > 0,…, x > 0
– загальна кількість ресурсів дорівнює x.
[2] x1 + x2 +… + x = x
Для цього загального завдання можуть бути побудовані рекуррентные
співвідношення
¦1
(x) = max {j1
(x1
)}, (2.5)
0 <=X1
<= X
¦k
(x) = max {jk
(xk
)+ ¦k
-1
(x – xk
)}. (2.6)
к = 2,3,…, N,
за допомогою яких перебуває її рішення.
При висновку цих рекурентних співвідношень, по суті, використався наступний принцип, оптимальна стратегія володіє тим властивістю, що стосовно будь-якого первісного стану після деякого етапу рішення сукупність наступних рішень повинна становити оптимальну стратегію. Цей принцип оптимальності лежить в основі всієї концепції динамічного програмування. Саме завдяки йому вдається при наступних переходах випробовувати не всі можливі варіанти, а лише оптимальні виходи. Рекурентні співвідношення дозволяють замінити надзвичайно трудомісткі обчислення максимуму по N змінним у вихідному завданні рішенням N завдань, у кожній з яких максимум перебуває лише по однієї змінній.
Таким чином, метод динамічного програмування дозволяє врахувати таку важливу особливість економічних завдань, як детермінованість більше пізніх рішень від більше ранніх.
Крім цих двох, досить детально розроблених методів, в економічних дослідженнях останнім часом стали застосовуватися безліч інших методів.
Одним з підходів до рішення економічних завдань є підхід, заснований на застосуванні нової математичної дисципліни – теорії ігор.
Суть цієї теорії полягає в тім, що гравець (учасник економічних взаємовідношень) повинен вибрати оптимальну стратегію залежно від того, якими він представляє дії супротивників (конкурентів, факторів зовнішнього середовища й т.д.). У залежності від того, наскільки гравець обізнаний про можливі дії супротивників, гри (а під грою тут розуміється сукупність правил, тоді сам процес гри це партія) бувають відкриті й закриті. При відкритій грі оптимальною стратегією буде вибір максимального мінімуму виграшу (у термінах Моргерштерна – «максі-міна») із всієї сукупності рішень, представлених у матричній формі. Відповідно супротивник буде прагне програти лише мінімальний максимум («міні – макс») який у випадку ігор з нульовою сумою буде дорівнює «максі-міну». В економіці ж частіше зустрічаються ігри з ненульовою сумою, коли виграють обоє гравця.
Крім цього в реальному житті число гравців рідко буває дорівнює всього двом. При більшому ж числі гравців з'являються можливості для кооперативної гри, коли гравці до початку гри можуть утворювати коаліції й відповідно впливати на хід гри.
Стратегії гравців не обов'язково повинні містити одне рішення, може бути так, що для досягнення максимального виграшу буде потрібно застосовувати змішану стратегію (коли дві або кілька стратегій застосовуються з якоюсь імовірністю). Крім того в закритих іграх теж потрібно враховувати ймовірність того або іншого рішення супротивника. Таким чином, у теорії ігор стало із апарата теорії імовірності, що згодом знайшов своє застосування в економічних дослідженнях у вигляді окремого методу – стохастичного моделювання.
Зміст методу стохастичного програмування складається у введенні в матрицю завдання або в цільову функцію елементів теорії імовірності. У цьому випадку звичайно береться просто середнє значення випадкової величини, узяте щодо всіх можливих станів.
У випадку не твердої, або двохєтапне зі стохастичного моделювання появляється можливість коректування отриманого плану після того, як стане відомим стан випадкової величини.
Крім цих методів застосовуються методи нелінійного, цілочисельного програмування й багато хто інших. Коротенько, сутність методу нелінійного програмування є в знаходженні або сідлової точки, або загального максимуму або мінімуму функції. Основна складність тут у труднощі визначення, чи є цей максимум загальним або локальним. Для цілочисельного моделювання основні труднощі саме й полягає в труднощі підбора цілого значення функції. Загальним для застосуванням цих методів на сучасному етапі є можливість часткової відомості їх до завдання лінійного моделювання. Можливо, у недалекому майбутньому буде знайдене якесь оригінальне рішення таких завдань специфічними методами, більше зручними, чим сучасні методи рішення подібних завдань (для яких вони є), і більше точні, ніж наближені рішення методами лінійного програмування.
3
.
Задача заміни обладнання
3.1 Алгоритм рішення задачі заміни обладнання
У цьому завданні як система S виступає встаткування. Стан цієї системи визначаються фактичним часом використання встаткування (його віком) t, тобто описуються єдиним параметром t.
Як керування виступають рішення про заміну й збереження встаткування, прийняті на початку кожного року. Позначимо через Xc рішення про збереження встаткування, а через Xз – рішення про заміну встаткування. Тоді завдання полягає в знаходженні такої стратегії керування, обумовленої рішеннями, прийнятими на початок кожного року, при якій загальний прибуток підприємства за вісім років є максимальною.
Процес рішення завдання здійснюється в такий спосіб. Береться період в N років. До цього часу встаткування відробило якусь кількість років і прийшло t0 віку.
Рішення завдання починається з останнього N-го року, складається пара функціональних рівнянь у припущенні, що прийшло старе встаткування без заміни:
1) розраховується доход від експлуатації встаткування при заміні;
2) розраховується доход від експлуатації встаткування протягом року за умови його старіння.
Друга гіпотеза: до N-ому року встаткування могло прийти заміненим у якомусь році, тоді складається пара рівнянь, у яких визначається доход за рік від експлуатації одиниці встаткування за умови заміни або збереження встаткування.
Крок другої: розглядаємо (N-1) рік.
Розглядаються дві гіпотези:
– прийшло старе встаткування без заміни;
– прийшло встаткування, що було замінено.
Крок третій: розглядається (N-2) рік при двох гіпотезах, складаються рівняння, розраховується доход.
Рішення триває по всіх кроках. На першому році буде одна гіпотеза, що прийшло старе встаткування, використовуване t0 років.
Під критерієм оптимальності може бути прийнятий будь-який економічний показник, якщо він добре підготовлений, тобто він повинен бути відчищений від факторів, що не залежать від роботи устаткування.
r(t) – вартість продукції, створеною одиницею устаткування віку t років за рік.
U(t) – витрати на протягом року одиниці встаткування віку t років.
С(t) – витрати на заміну одиниці устаткування віку t років (витрати на придбання, налагодження за винятком залишкової вартості старого встаткування).
і – рік установки нового обладнання.
Доход заміни встаткування розраховується:
f' = r(t) – U(t) – C(t) (3.1)
Доход від збереження встаткування:
f'' = r(t) – U(t) (3.2)
Якщо f' > f'', то встаткування необхідно замінити, якщо f' ≤ f'' – залишити.
Крок 1-й: N-й рік.
Гіпотеза 1: прийшло старе встаткування віку N+t0 років.
Тоді доход за N-й рік за умови заміни або збереження встаткування:
 (3.3) (3.3)
Гіпотеза 2: прийшло нове обладнання.
 (3.4) (3.4)
Візьмемо N-t-й рік:
 (3.5) (3.5)
Крок 2-й: (N-1) – й рік.
Розраховується сумарний умовний доход, за умови заміни або збереження.
Гіпотеза 1: прийшло старе устаткування.
 (3.6) (3.6)
Гіпотеза 2: прийшло нове устаткування.
 (3.7) (3.7)
3.2 Контрольний приклад
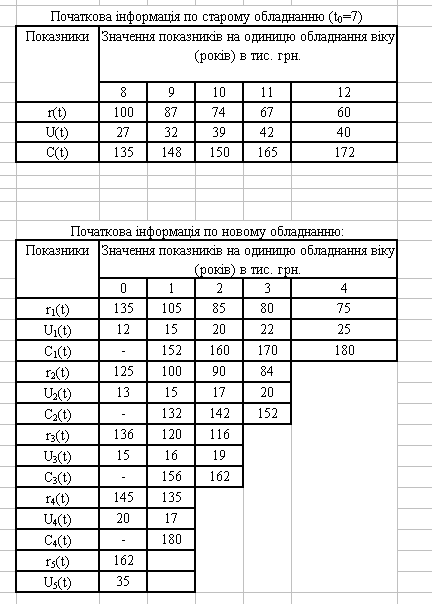
Для контрольного прикладу необхідно сформулювати дані про показники, які буде мати старе та нове обладнання на протязі певного періоду часу, в нашому випадку 5 років. Тобто, треба визначити, вартість продукції, виробленою одиницею обладнання за рік – r(t), витрати на експлуатацію обладнання протягом року – U(t), витрати на заміну одиниці устаткування – С(t) (див. Додаток А).
Задачу будемо розглядати в п’ять етапів. Тобто в кожному році ми будемо шукати найоптимальніші варіанти заміни обладнання.
На першому етапі ми розраховуємо за п’ять років максимальний прибуток, тобто за t=12,1,2,3,4.
Розраховується за допомогою формул (3.3) та (3.4) відповідно до старого та нового обладнання. По розрахунках робимо висновок заміняти чи зберегти обладнання. На цьому етапі ми робимо висновок зберегти обладнання. (див. Додаток Б)
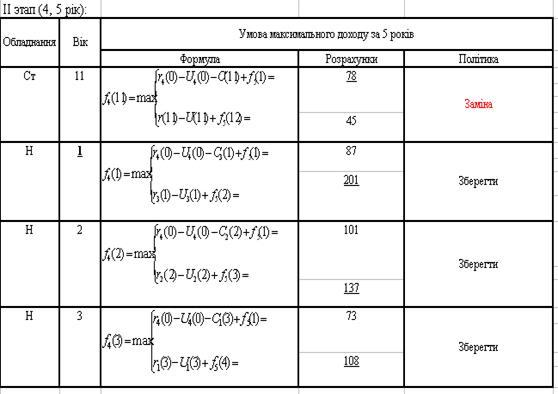
На другому етапі ми розраховуємо ефективність, коли t=11,1,2,3, для цього використовуємо формули (3.6) (3.7), також відповідно для нового та старого обладнання. Вирішуємо, що t=11 потрібно замінити, а інші залишити (див. Додаток В).
На третьому, четвертому та п’ятому етапі також використовуємо формули (3.6) та (3.7), відповідно до старого та нового обладнання, та робимо висновки, щодо заміни обладнання (див. Додаток Г, Д, Є).
Після розрахунку максимальних прибутків на кожному з етапів ми отримуємо:
– в 1 році зберегти обладнання, при цьому дохід складе (300–263)=37 тис. грн.;
– на 2 рік, зберегти при доході (263–172)=91 тис. грн.;
– на 3 році – змінити, при збитку (172–201)=55 тис. грн.;
– на 4 рік – зберегти, при доході (201–97)=104 тис. грн.,
– на 5 році – зберегти, при доході 97 тис. грн.
Така політика являється оптимальною. Вона забезпечує максимальний прибуток 300 тис. грн.
Висновки
Динамічне програмування – це область математичного програмування, що включає сукупність прийомів і засобів для знаходження оптимального рішення, а також оптимізації кожного кроку в системі й виробленні стратегії керування, тобто процес керування можна представити як багатокроковий процес. Динамічне програмування, використовуючи поетапне планування, дозволяє не тільки спростити рішення завдання, але й вирішити ті з них, до яких не можна застосувати методи математичного аналізу. Спрощення рішення досягається за рахунок значного зменшення кількості досліджуваних варіантів, тому що замість того, щоб один раз вирішувати складне різноманітне завдання, метод поетапного планування припускає багаторазове рішення щодо простих завдань. Плануючи поетапний процес, виходять із інтересів усього процесу в цілому, тобто при ухваленні рішення на окремому етапі завжди необхідно мати у виді кінцеву мету.
Однак динамічне програмування має й свої недоліки. На відміну від лінійного програмування, у якому симплексний метод є універсальним, у динамічному програмуванні такого методу не існує. Кожне завдання має свої труднощі, і в кожному випадку необхідно знайти найбільш підходящу методику рішення. Недолік динамічного програмування полягає також у трудомісткості рішення багатомірних завдань. Завдання динамічного програмування повинна задовольняти дві умови. Першу умову звичайно називають умовою відсутності післядії, а друге – умовою адитивності цільової функції завдання.
На практиці зустрічаються такі завдання планування, у яких помітну роль грають випадкових факторів, що впливають як на стан системи, так і на виграш. Існує різниця між детермінованою й стохастичним завданнями динамічного програмування. У детермінованому завданні оптимальне керування є єдиним і вказується заздалегідь як тверда програма дій. У стохастичним завданню оптимальне керування є випадковим і вибирається в ході самого процесу залежно від випадково сформованої ситуації. У детермінованій схемі, проходячи процес по етапах від кінця до початку, теж перебуває на кожному етапі цілий ряд умовних оптимальних керувань, але із всіх цих керувань, в остаточному підсумку здійснювалося тільки одне. У стохастичній схемі це не так. Кожне з умовних оптимальних керувань може виявитися фактично здійсненим, якщо попередній хід випадкового процесу приведе систему у відповідний стан.
Принцип оптимальності є основою поетапного рішення завдань динамічного програмування. Типовими представниками економічних завдань динамічного програмування є так називані завдання виробництва й зберігання, завдання розподілу капіталовкладень, завдання календарного виробничого планування й інших. Завдання динамічного програмування застосовуються в плануванні діяльності підприємства з урахуванням зміни потреби в продукції в часі. В оптимальному розподілі ресурсів між підприємствами в напрямку або в часі.
Опис характеристик динамічного програмування й типів завдань, які можуть бути сформульовані в його рамках, по необхідності повинне бути дуже загальним і трохи невизначеним, тому що існує неозора безліч різних завдань, що укладаються в схему динамічного програмування. Тільки вивчення великої кількості прикладів дає виразне розуміння структури динамічного програмування.
Перелік посилань
1. Акулич И.Л. Математичне програмування в прикладах і завданнях. – М.: Вища школа, 1993.
2. Дудорин В.И. Моделювання в завданнях керування виробництвом.-М.: Статистика, 1980.
3. Дослідження операцій в економіці: навчальний посібник для вузів / під ред. Кремера Н.Ш. – М.: Банки й Біржі, ЮНИТИ, 1997.
4. http://www.dis.ru/manag/arhiv/2002/
5. http://www.math.mrsu.ru/programs/ivt/e-learn/7.html#zachin
Додаток А
Додаток Б

Додаток В
Додаток Г
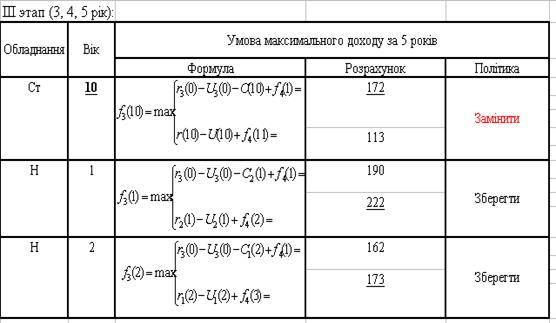
Додаток Д

|